pavani

NEET Physics For Electrostatic Potential And Capacitance Multiple Choice Questions

Question 1. In a certain region of space with a volume of 0.2 m³, the electric potential is found to be 5 V throughout. The magnitude of the electric field in this region is:

1. 0.5 N/C
2. 1 N/C
3. 5 N/C
4. zero

Answer: 1. 0.5 N/C

Given Volume, V=0.2 \(\mathrm{~m}^3\)

Electric potential =5 \(\mathrm{~V}\) (constant)

Electric field =?

Here Electric field, E=\(-\frac{d v}{d r}\)

Here V=5\(\mathrm{~V}\) and constant

E=\(-\frac{d(5)}{d t}\)

= \(\frac{d(\text { constant })}{d t}\)=0

Question 2. A bullet of mass 2 g is having 2 μc. Through what potential difference must it be accelerated, starting from rest, to acquire a speed of 10 m/s?

1. 5 kV
2. 50 kV
3. 5 V
4. 50 V

Answer: 2. 50 kV

Here we apply, \(\frac{1}{2} m v^2\)=q V

V =\(\frac{1}{2} \times \frac{2 \times 10^{-3} \times 10 \times 10}{2 \times 10^{-6}}\)

=50 kV

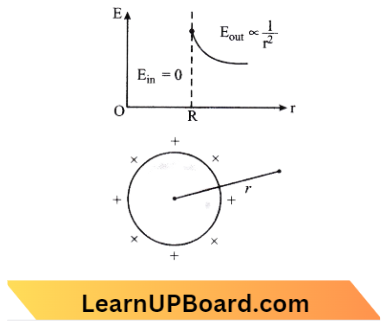
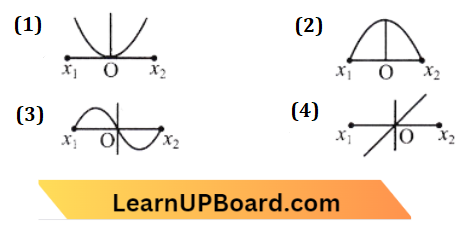
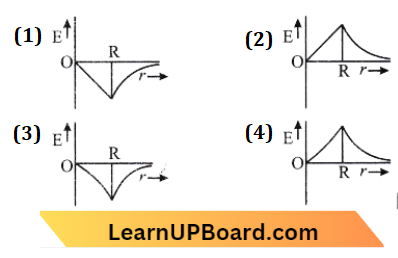
Question 3. The variation of electrostatic potential with radial distance r from the centre of a positively charged metallic thin shell of radius R is given by the graph:

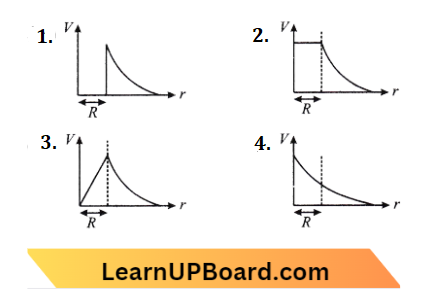
Answer: 3.

Since electric potential remains constant inside the metallic spherical shell which is the same as at the surface of a spherical shell. Outside the spherical shell V \(\propto \frac{1}{r}\). So, (b) is the r variation of potential (V) with distance r

Question 4. The electric potential at a point in free space due to charge Q coulomb is Q x 10¹¹ V. The electric field at that point is:

1. 4 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)
2. 12 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{20} \mathrm{~V} / \mathrm{m}\)
3. 4 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)
4. 12 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)

Answer: 1. 4 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)

Since, V =\(\frac{Q}{4 \pi \varepsilon_0 r}\)

Given, V =\(Q \times 10^{11}\)

r =\(\frac{1}{4 \pi \varepsilon_0 \times 10^{11}}\)

Now \(\mathrm{E} =\frac{V}{r}\)

E = \(Q \times 10^{11} \times 4 \pi \varepsilon_0 \times 10^{11}\)

= 4 \(\pi \varepsilon_0 \times 10^{22} \mathrm{~V} / m\)

Read and Learn More NEET Physics MCQs

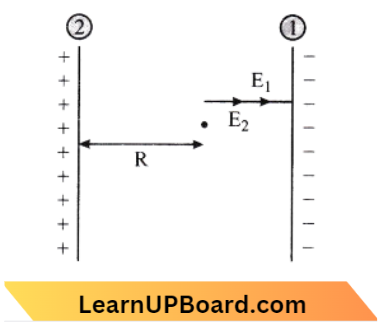
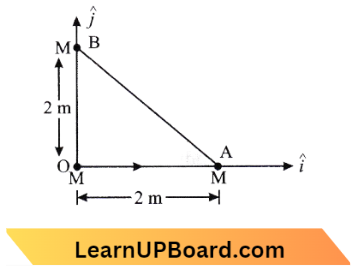
Question 5. As per the diagram a point charge + q is placed at the origin O. Work done in taking another point charge – Q from the point A [coordinate (0, a)] to another point B [coordinates (a, 0)] along the straight path AB is:

1. zero
2. \(\left(\frac{q Q}{4 \pi \varepsilon_0} \frac{1}{a^2}\right) \cdot \sqrt{2}\) a
3. \(\left(\frac{-q Q}{4 \pi \varepsilon_0} \frac{1}{a^2}\right) \cdot \sqrt{2}\) a
4. \(\left(\frac{q Q}{4 \pi \varepsilon_0} \frac{1}{a^2}\right) \cdot \frac{a}{\sqrt{2}}\)

Answer: 1. zero

Work done is equal to zero because the potential of A and B are the same \(\frac{1}{4 \pi \epsilon_0} \frac{q}{a}\)

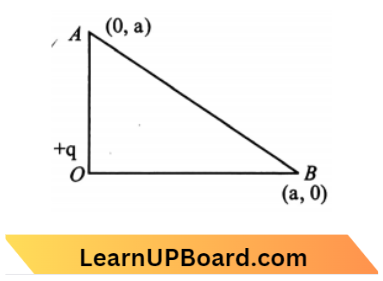
No work is done if a particle does not change its potential energy.

The initial potential energy = final potential energy.

Question 6. A short electric dipole has a dipole moment of 16 x 10^-9 cm. The electric potential due to the dipole at a point at a distance of 0.6 m from the centre of the dipole, situated on a line making an angle of 60° with the dipole axis is:\(\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\)

1. 200 V
2. 400 V
3. zero
4. 50 V

Answer: 1. 200 V

Given the electric dipole moment,

P= \(16 \times 10^{-9} \mathrm{~cm}\)

Distance, r=0.6 \(\mathrm{~m}, Angle \theta=60^{\circ}\)

⇒ \(\cos 60^{\circ}=\frac{1}{2}\)

The Electric potential at a point at a distance k at some angle \(\theta\) from electric dipole is V and

V =\(\frac{P \cos \theta}{4 \pi \varepsilon_0 r^2}\)

= 9 \(\times 10^9 \times \frac{16 \times 10^{-9} \times \frac{1}{2}}{(0.6)^2}\)

= 2 \(\times 10^2=200 \mathrm{~V}\)

Question 7. Two hollow conducting spheres of radii R₁ and R₀ (R₁>>R₂) have equal charges. The potential would be:

1. more on the bigger sphere
2. more on the smaller sphere
3. equal on both the spheres
4. dependent on the material property of the sphere

Answer: 2. more on the smaller sphere

For a hollow sphere, an electric potential is \(\mathrm{V}=\frac{\mathrm{kq}}{\mathrm{R}}\)

For sphere 1, \(V_1=\frac{k q}{R_1}\)

For sphere 1, \(V_2=\frac{k q}{R_2}\)

As \(\mathrm{R}_1 \gg \mathrm{R}_2\),

⇒ \(\mathrm{V}_1 \ll \mathrm{V}_2\).

So, the potential is more on the smaller sphere.

Question 8. Two charged spherical conductors of radius R₁ and R₂ are connected by a wire. Then the ratio of surface charge densities of the spheres \((\sigma_1 / \sigma_2)\) is:

1. \(\frac{R_1}{R_2}\)
2. \(\frac{R_2}{R_1}\)
3. \(\sqrt{\left(\frac{R_1}{R_2}\right)}\)
4. \(\frac{R_1^2}{R_2^2}\)

Answer: 2. \(\frac{R_2}{R_1}\)

Given,Radius =\(R_1 \text { and } R_2 \)

Surface density =\(\sqrt{\sigma_1} \text { and } \sqrt{\sigma_2}\)

⇒ \(\mathrm{~V}_1=\mathrm{V}_2\)

⇒ \(\frac{k q_1}{\mathrm{R}_1}=\frac{k q_2}{\mathrm{R}_2} \)

⇒ \(\frac{q_1}{q_2}=\frac{R_1}{R_2}\)  → Equation 1

Since the spheres are connected by wire. Hence, the charge on them will be equal.

⇒ \(q_1 =q_2\)

⇒ \(q_1 =\sigma_1 \mathrm{~A}_1, q_2=\sigma_2 \mathrm{~A}_2\)

⇒ \(q_1 =\sigma_1 4 \pi \mathrm{R}_1^2\)

⇒ \(q_2 =\sigma_2 4 \pi \mathrm{R}_2^2\)

⇒ \(\frac{\sigma_1}{\sigma_2} =\frac{\frac{q_1}{4 \pi \mathrm{R}_1^2}}{\frac{q_2}{4 \pi \mathrm{R}_2^2}}\)

∴ \(\frac{\sigma_1}{\sigma_2} =\frac{\mathrm{R}_2^2}{\mathrm{R}_1^2} \times \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{\mathrm{R}_2}{\mathrm{R}_1}\)

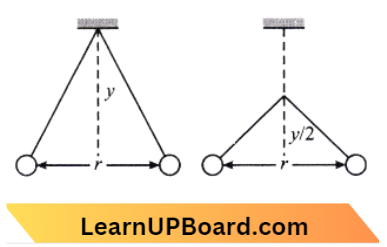
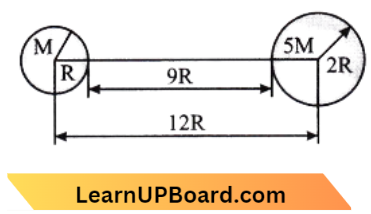
Question 9. Twenty-seven drops of the same size are charged at 220 V each. They combine to form a bigger drop. The potential for a bigger drop is:

1. 660 V
2. 1320 V
3. 1520 V
4. 1980 V

Answer: 4. 1980 V

Given, the No. of drops = 27

Radius = r

Voltage (F)= 220 V

Its total Radius = R

V=?

Bigger sphere volume \(V_B=\frac{4}{3} \pi \mathrm{R}^3\)

Smaller sphere volume \(V_{\mathrm{s}}=\frac{4}{3} \pi r^3\)

⇒ \(27 \frac{4}{3} \pi r^3 =\frac{4}{3} \pi \mathrm{R}^3 \)

⇒ \(27 r^3 =\mathrm{R}^3\)

⇒ \(\mathrm{R} \) =3 r

Charge \(q_1\) on smaller sphere,

⇒ \(\mathrm{V}_0=\frac{q}{4 \pi \varepsilon_0 r}\)

⇒ \(q_1=\mathrm{V}_0 4 \pi \varepsilon_0 r\)

Charge \(q_2\) on bigger sphere,

⇒ \(q_2 =27 q_1\)

∴ \(\mathrm{V} =\frac{q_2}{4 \pi \varepsilon_0 \mathrm{R}}\)

Question 10. Two metal spheres, one of radius R and the other of radius 2R respectively have the same surface charge density \(\sigma\). They are brought in contact and separated. The new charge densities on them will be:

1. \(\sigma_1=\frac{5}{6} \sigma, \sigma_2=\frac{5}{2} \sigma\)
2. \(\sigma_1=\frac{5}{2} \sigma, \sigma_2=\frac{5}{6} \sigma\)
3. \(\sigma_1=\frac{5}{2} \sigma, \sigma_2=\frac{5}{3} \sigma\)
4. \(\sigma_1=\frac{5}{3} \sigma, \sigma_2=\frac{5}{6} \sigma\)

Answer: 4. \(\sigma_1=\frac{5}{3} \sigma, \sigma_2=\frac{5}{6} \sigma\)

Given

Two metal spheres, one of radius R and the other of radius 2R respectively have the same surface charge density \(\sigma\). They are brought in contact and separated.

⇒ \(\sigma_1=\frac{5}{3} \sigma, \sigma_2=\frac{5}{6} \sigma\)

We know that surface charge density

⇒ \(\sigma=\frac{q}{A}=\frac{q}{4 \pi R^2}\)

q= \(\sigma .4 \pi R^2\)

Before contact of both the spheres X and Y.

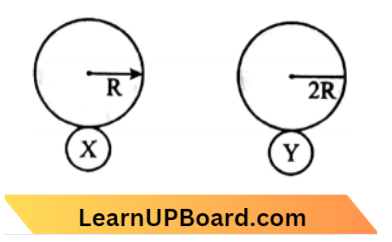
For X, \(q_1 =\sigma .4 \pi R^2 \)

⇒ \(q_2 =4 q_1\)

After Contact, \(q_2=\sigma .4 \pi(2 R)^2\)

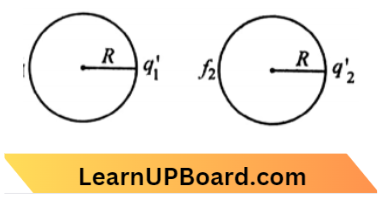
Here \(\sigma_1=\frac{q_1^{\prime}}{4 \pi R^2}\) and

⇒ \(\sigma_2=\frac{q_2^{\prime}}{4 \pi R\left(2 R^2\right)}\)

Again we know that, V=\(\frac{k q}{\mathrm{R}}\)

So, \(\frac{k q_1^{\prime}}{\mathrm{R}}=\mathrm{K}\)

So, after contact, we can say, \(q_1^{\prime}+q_2^{\prime}=q_1+q_2=5 q_1 \)

⇒ \(q_1{ }^{\prime}+q_2{ }^{\prime}=5 \times \sigma 4 \pi \mathrm{R}^2\)

3 \(q_1^{\prime}=5 \times 6 \times 4 \pi \mathrm{R}^2 \)

3 \(q_1^{\prime}=5 \times 6 \times 4 \pi \mathrm{R}^2 \)

and \(q_2^{\prime}=2 q_1^{\prime}=\frac{10}{3} \times \sigma 4 \pi \mathrm{R}^2\)

Putting the value of \(q_1{ }^{\prime} and q_2\)

∴ \(\sigma_1=\frac{5}{3} \sigma \text { and } \sigma_2=\frac{5}{6} \sigma\)

Question 11. Four point charges -Q, – q, 2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero, is:

1. Q=-q
2. Q=\(-\frac{1}{q}\)
3. Q=q
4. Q=\(\frac{1}{q}\)

Answer: 1. Q=-q

According to the question when the potential at the centre is zero,

⇒ \(V_1+V_2+V_3+V_4\)=0

⇒ \(\frac{\mathrm{KQ}}{r}-\frac{\mathrm{K} q}{r}+\frac{\mathrm{K}(2 \mathrm{Q})}{r}+\frac{\mathrm{K} 2 q}{r}\) =0

⇒ \(-Q-q+2 q+2 Q \)=0

Q =\(-\mathrm{q}\)

Question 12. Four electric charges + q, + q, – q and – q are placed at the comers of a square of side 2L (see figure). The electric potential at point A mid-way between the two charges + q and q, is:

1. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1+\frac{1}{\sqrt{5}}\right)\)
2. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)
3. zero
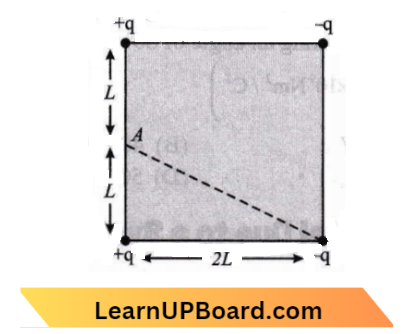
4. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}(1+\sqrt{5})\)

Answer: 2. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)

⇒ \(V_A =\frac{k q}{L}+\frac{k q}{L}-\frac{k q}{\sqrt{5} L}-\frac{k q}{\sqrt{5} L}\)

= \(\frac{2 k q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)

= \(\frac{2 q}{L} \times \frac{1}{4 \pi \varepsilon_0}\left(1-\frac{1}{\sqrt{5}}\right)\)

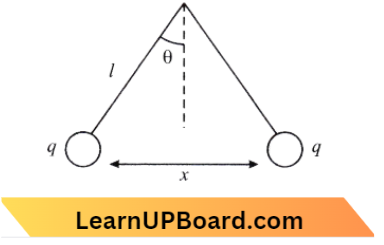
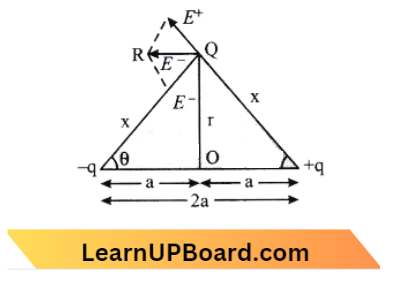
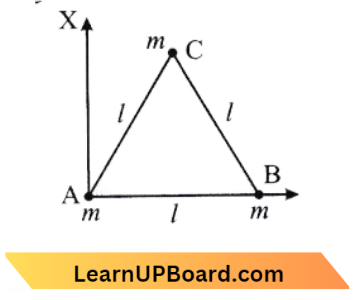
Question 13. Three charges, each + q, are placed at the comers of an isosceles triangle ABC of sides BC and AC, 2a. D and E are the mid j oint of BC and CA. The work done in taking a charge Q from D to E is:

1. \(\frac{q Q}{8 \pi \varepsilon_0 a}\)
2. \(\frac{q \mathrm{Q}}{4 \pi \varepsilon_0 a}\)
3. zero
4. \(\frac{3 q Q}{4 \pi \varepsilon_0 a}\)

Answer: 3. zero

Given

Three charges, each + q, are placed at the comers of an isosceles triangle ABC of sides BC and AC, 2a. D and E are the mid j oint of BC and CA

The situation is shown in the diagram,

From the figure, A C =\(B C(\text { given })\)

⇒ \(V_D =V_E\)=V

W =\(Q\left(V_{\mathrm{E}}-V_{\mathrm{D}}\right)\)

=Q(V-V)

W = 0

Question 14. Three concentric spherical shells have radii a, b and c (a< b <c) and have surface charge densities a, – a and o respectively. If V_A, V_B and V_C denote the potentials of the three shells then for c = a + b, we have:

1. \(V_C=V_A \neq V_B\)
2. \(V_C=V_B \neq V_A\)
3. \(V_C \neq V_B \neq V_A\)
4. \(V_C=V_B=V_A\)

Answer: 1. \(V_C=V_A \neq V_B\)

⇒ \(V_A=\frac{1}{4 \pi \varepsilon_0}\left\{\frac{q_A}{a}+\frac{q_B}{b}+\frac{q_C}{c}\right\}\)

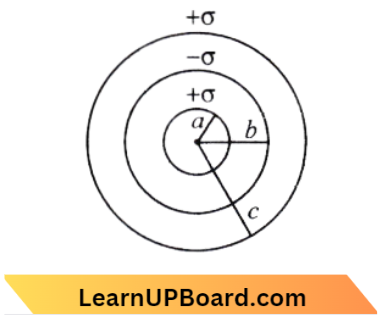
=\(\frac{4 \pi}{4 \pi \varepsilon_0}\left\{\frac{a^2 \sigma}{a}-\frac{b^2 \sigma}{b}+\frac{c^2 \sigma}{c}\right\}\)

⇒ \(V_A =\frac{1}{\varepsilon_0}\left\{\frac{a^2 \sigma}{a}-\frac{b^2 \sigma}{b}+\frac{c^2 \sigma}{c}\right\}\)

⇒ \(V_B =\frac{1}{\varepsilon_0}\left\{\frac{a^2 \sigma}{b}-\frac{b^2 \sigma}{b}+\frac{c^2 \sigma}{c}\right\}\)

⇒ \(V_C =\frac{1}{\varepsilon_0}\left\{\frac{a^2 \sigma}{c}-\frac{b^2 \sigma}{c}+\frac{c^2 \sigma}{c}\right\}\)

Using c=a+b, \(V_A=\frac{2 a \sigma}{\varepsilon_0} \)

⇒ \(V_B =\frac{\sigma}{\varepsilon_0}\left(\frac{a^2}{b}+a\right)=\frac{\sigma}{\varepsilon_0} \frac{a c}{b}\)

⇒ \(V_C \frac{\sigma}{\varepsilon_0}\left[\frac{(a+b)(a-b)}{c}+c\right]\)

= \(\frac{\sigma}{\varepsilon_0}(a-b+c)=\frac{2 a \sigma}{\varepsilon_0} \)

⇒ \(V_B =\frac{1}{4 \pi \varepsilon_0} \frac{\sigma 4 \pi c^2}{b}-\frac{1}{4 \pi \varepsilon_0} \frac{\sigma 4 \pi c^2}{b}\)

= \(\frac{\sigma}{\varepsilon_0}\left(\frac{a^2}{b}-b+c\right)\)

Similarly, \(V_C =\frac{\sigma}{\varepsilon_0}(2 a)\)

∴ \(V_A =V_C \neq V_B\)

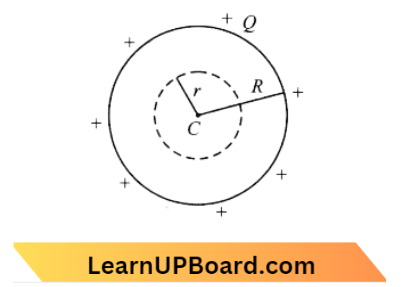
Question 15. Two concentric spheres of radii R and r have similar charges with equal surface charge densities (o). What is the electric potential at their common centre?

1. \(\frac{\sigma}{\varepsilon_0}\)
2. \(\frac{\sigma}{\varepsilon_0}(R-r)\)
3. \(\frac{\sigma}{\varepsilon_0}(R+r)\)
4. None of these

Answer: 3. \(\frac{\sigma}{\varepsilon_0}(R+r)\)

Let the charges on the spheres be Q and q respectively. The potential at the common center,

V =\(\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R}\right)+\frac{1}{4 \pi \varepsilon_0}\left(\frac{q}{r}\right)\)

= \(\frac{1}{\varepsilon_0}\left[\frac{Q}{4 \pi R^2} \times R+\frac{q}{4 \pi r^2} \times r\right]\)

But, \(\frac{Q}{4 \pi R^2} =\frac{q}{4 \pi R^2}=\sigma\)

⇒ \(\mathrm{V} =\frac{1}{\varepsilon_0}[\sigma R+\sigma r]\)

=\(\frac{\sigma}{\varepsilon_0}(R+r)\)

Question 16. The angle between the electric lines of force and the equipotential surface is:

1. 0°
2. 45°
3. 90°
4. 180°

Answer: 3. 90°

The angle between the electric lines of force and the equipotential surface is 90°.

Question 17. The diagrams below show regions of equipotentials: A positive charge is moved from A to B in each diagram.

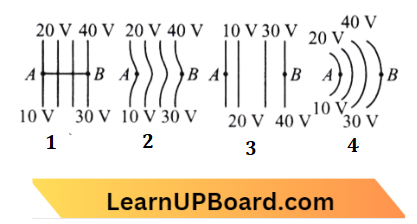
1. Maximum work is required to move q in Figure (3).
2. In all four cases, the work done is the same.
3. Minimum work is required to move q in Figure (1).
4. Maximum work is required to move q in Figure (2).

Answer: 2. In all the four cases, the work done is the same.

Work done, W = q \(\Delta V\)

∴ \(\Delta V\) is the same in all the cases so the work done is the same in all the cases.

Question 18. If potential (in volts) in a region is expressed as V(x, y, z) = 6xy -y + 2yz. the electric field in (N/C) at point (1,1, 0) is:

1. \(-(3 \hat{i}+5 \hat{j}+3 \hat{k})\)
2. \(-(6 \hat{i}+5 \hat{j}+2 \hat{k})\)
3. \(-(2 \hat{i}+3 \hat{j}+\hat{k})\)
4. \(-(6 \hat{i}+9 \hat{j}+\hat{k})\)

Answer: 2. \(-(6 \hat{i}+5 \hat{j}+2 \hat{k})\)

From the question, Potential in a region,

⇒ \(V_{(x, y, z)}=6 x y-y+2 y z\)

Electric field, E= \(-\frac{\partial V}{\partial x} \hat{i}-\frac{\partial V}{\partial y} \hat{j}-\frac{\partial V}{\partial z} \hat{k}\)

= \(-6 y \hat{i}-(6 x-1) \hat{j}-2 y \hat{k}\)

⇒ \(E_{(1,1,0)} =(6 \times 1) \hat{i}-(6 \times 1-1) \hat{j}-2 \times 1 \hat{k}\)

= \(-(6 \hat{i}+5 \hat{j}+2 \hat{k}) \mathrm{N} / \mathrm{C}\)

Question 19. In a region the potential is represented by V(x, y, z) = 6x – xy – 8y + 6yz, where V is in volts and x, y, z are in metres. The electric force experienced by a charge of 2 coulomb situated at point (1, 1,1) is:

1. \(6 \sqrt{5} \mathrm{~N}\)
2. 30 \(\mathrm{~N}\)
3. 24 \(\mathrm{~N}\)
4. 4 \(\sqrt{35} \mathrm{~N}\)

Answer: 4. 4 \(\sqrt{35} \mathrm{~N}\)

It is given,

V=6 x-8 x y-8 y+6 y z

We know that, E =\(\frac{\mathrm{d} V}{\mathrm{~d} x}\)  → Equation 1

⇒ \(E_X =\frac{\mathrm{d} V}{\mathrm{~d} x}=6-8 y \)

⇒ \(E_Y =\frac{\mathrm{d} V}{\mathrm{~d} y}=-8 x-8+6 \mathrm{z}\) →  Equation 2

⇒ \(E_{\mathrm{z}} =\frac{d V}{d z}\)=6 y

The values of \(E_X, E_Y\) and \(E_Z\) at (1,1,1) are,

⇒ \(E_X =6-8 \times 1\)=-2

⇒ \(E_Y =-8 \times 1-8+6 \times 1\)=-10

⇒ \(E_Z =6 \times 1\)=6

⇒ \(E_{\text {net }} =\sqrt{(2)^2+(10)^2+(6)^2}\)

=\(\sqrt{4+100+36}=\sqrt{140} \)

=\(\sqrt{35 \times 4}=2 \sqrt{35} \mathrm{~N} / \mathrm{C}\)

F =\(q \cdot E_{n e t}\)

=\(2 \times(2 \sqrt{35})=4 \sqrt{35} \mathrm{~N}\)

Question 20. The electric potential V at any points (x, y, z), all in metres in spaces is given V = 4×2 volt. The electric field at the point (1, 0, 2) in volt/metre is:

1. 8 along the positive X-axis
2. 16 along the negative X-axis
3. 16 along the positive X-axis
4. 8 along the negative X-axis

Answer: 4. 8 along the negative X-axis

It is given that, V=4 x^2

Then We have,E =\(-\left[\hat{i} \frac{\partial V}{\partial x}+\hat{j} \frac{\partial V}{\partial y}+\hat{k} \frac{\partial V}{\partial z}\right]\)

= \(\hat{i} \frac{\partial V}{\partial x}=-\hat{i} \frac{\partial V}{\partial x}\left(4 x^2\right)\)

= \(-8 x \mathrm{Vm}^{-2}\)

∴ \(\mathrm{E}_{(1,0,2)} =-8 \times 1=-8 \hat{i} \cdot \mathrm{Vm}^{-1}\)

Question 21. The electric potential at a point (x, y, z) is given by, \(V=-x^2 y-x z^3+4\). The electric field \(\vec{E}\) at that point is:

1. \(\vec{E}=\left(2 x y+z^3\right) \hat{i}+x^2 \hat{j}+3 x z^2 \hat{k}\)
2. \(\vec{E}=2 x y \hat{i}+\left(x^2+y^2\right) \hat{j}+\left(3 x z-y^2\right) \hat{k}\)
3. \(\vec{E}=z^3 \hat{i}+x y z \hat{j}+z^2 \hat{k}\)
4. \(\vec{E}=\left(2 x y-z^3\right) \hat{i}+x y^2 \hat{j}+3 z^2 x \hat{k}\)

Answer: 1. \(\vec{E}=\left(2 x y+z^3\right) \hat{i}+x^2 \hat{j}+3 x z^2 \hat{k}\)

We know that, E =\(-\frac{d V}{d r}=\left[-\frac{\partial v}{\partial x} \hat{i}-\frac{\partial v}{\partial y} \hat{j}-\frac{\partial v}{\partial z} \hat{k}\right]\)

= \(\left[\hat{i}\left(2 x y+z^3\right)+\hat{j} x^2+\hat{k} 3 x z^2\right]\)

Question 22. Charges +q and -q are placed at points A and B respectively which are a distance 2L apart, C is the midpoint between A and B. The work done in moving a charge +Q along the semicircle CRD is:

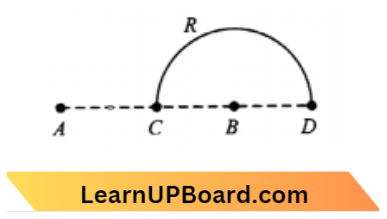
1. \(\frac{q Q}{2 \pi \varepsilon_0 L}\)
2. \(\frac{q Q}{6 \pi \varepsilon_0 L}\)
3. \(\frac{q Q}{3 \pi \varepsilon_0 L}\)
4. \(\frac{q Q}{4 \pi \varepsilon_0 L}\)

Answer: 2. \(\frac{q Q}{6 \pi \varepsilon_0 L}\)

W=\(\Delta U=\mathrm{Q}\left(V_D-V_C\right)\)

where, \(V_C\)=0

W =\(Q\left[\frac{q}{4 \pi \varepsilon_0(3 L)}-\frac{q}{4 \pi \varepsilon_0(L)}\right]\)

= \(-\frac{Q q}{6 \pi \varepsilon_0 L}\)

The potential at C is zero because the charges are equal and opposite and the distances are the same. Potential at D due to – q is greater than that at A (+q) because D is closer to B.

∴ It is negative.

Question 23. Two charges q₁ and q₂ are placed 30 cm apart, as shown in the figure. A third charge q₃ is moved along the arc of a circle of radius 40 cm from C to D. The change in the potential energy of the system is \(\frac{V_3}{4 \pi \varepsilon_0} k\)

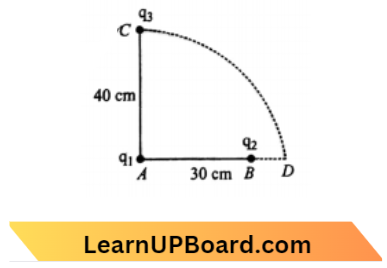
1. \(8 q_1\)
2. \(6 q_1\)
3. \(8 q_2\)
4. \(6 q_2\)

Answer: 3. \(8 q_2\)

⇒ \(V_i=\frac{1}{4 \pi \epsilon_0}\left[\frac{q_1 q_3}{(0.4)}+\frac{q_1 q_2}{(0.3)}+\frac{q_2 q_3}{(0.5)}\right] \)

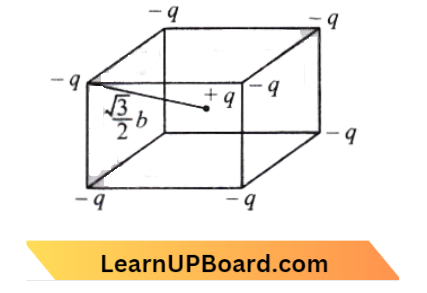
⇒ \(\Delta V =V_f-V_{\mathrm{i}}\)

= \(\frac{1}{4 \pi \epsilon_0} q_2 q_3\left(\frac{1}{0.1}-\frac{1}{0.5}\right)\)

= \(\frac{q_2 q_3}{4 \pi \epsilon_0}\left(10^{-2}\right)\)

= \(\frac{q_3}{4 \pi \epsilon_0}\left(8 q_2\right)\)

k =\(8 q_2\)

Question 24. Identical charges (- q) are placed at each comer of a cube of side ‘b’ then the electrical potential energy of charge (+ q) which is placed at the centre of the cube will be:

1. \(\frac{-4 \sqrt{2} q^2}{\pi \varepsilon_0 b}\)
2. \(\frac{-8 \sqrt{2} q^2}{\pi \varepsilon_0 b}\)
3. \(\frac{-4 q^2}{\sqrt{3} \pi \varepsilon_0 b}\)
4. \(\frac{8 \sqrt{2} q^2}{4 \pi \varepsilon_0 b}\)

Answer: 3. \(\frac{-4 q^2}{\sqrt{3} \pi \varepsilon_0 b}\)

The distance between the charge -q and +q is,

r= \(\sqrt{\frac{(\sqrt{2} b)^2+(b)^2}{2}}=\frac{\sqrt{3}}{2} b\)

The electric potential energy of charge +q is,

V = 8 \(\times \frac{1}{4 \pi \varepsilon_0} \frac{q(-q)}{r}\)

= 8 \(\times \frac{1}{4 \pi \varepsilon_0} \frac{q(-q)}{\frac{\sqrt{3}}{2} b}\)

U =\(\frac{-4 q^2}{\sqrt{3} \pi \varepsilon_0 b}\)

Question 25. In bringing an electron towards another electron, the electrostatic potential energy of the system:

1. decreases
2. increases
3. remains same
4. becomes zero

Answer: 2. increases

The electron is charged negatively. When an electron passes another electron, the same negative charges produce a repulsive force between them. As a result, work is done against this repulsive force to bring them closer together. Electrostatic potential energy is used to store the work.

As a result, the system’s electrostatic potential energy increases. Since the electrostatic potential energy of a system of two electrons, \(\mathrm{U}=\frac{1}{4 \pi \varepsilon_0} \frac{(-e)(-e)}{r}=\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r}\)

R decreases, and potential energy U increases.

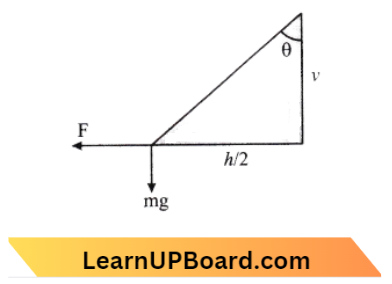
Question 26. A dipole is placed in an electric field as shown. In which direction will it move?

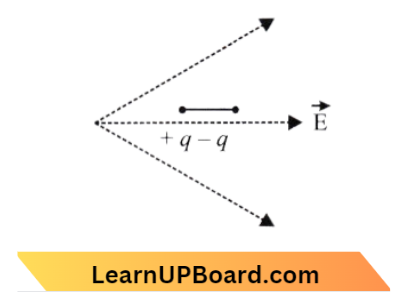
1. Towards the left, its potential energy will increase.
2. Towards the right, its potential energy will decrease.
3. Towards the left, its potential energy will decrease.
4. Towards the right, its potential energy will increase.

Answer: 3. Towards the left its potential energy will decrease.

Since the electric field is growing against the dipole direction hence the dipole will move towards the left due to a decrease in its potential energy.

Question 27. An electric dipole of dipole moment p is aligned parallel to a uniform electric field E. The energy required to rotate the dipole by 90° is:

1. \(p^2 E\)
2. pE
3. infinity
4. \(p E^3\)

Answer: 2. pE

The potential energy of the dipole

U = \(-p E\left(\cos \theta_2-\cos \theta_1\right)\)

⇒ \(\theta_2 =0^{\circ}\)

=\(-p E\left(\cos 90^{\circ}-\cos 0^{\circ}\right)\)

U = PE

Question 28. An electric dipole of dipole moment \(\vec{p}\) is lying along a uniform electric field \(\vec{E}\). The work done in rotating the dipole by:

1. pE
2. \(\sqrt{2} p E\)
3. pE / 2
4. 2PE

Answer: 1. pE

Work done, W =\(\int_0^\theta P E \sin \theta d \theta \)

= P E\((1-\cos \theta)\)

Since, \(\theta=90^{\circ}\)

W =\(P E\left(1-\cos 90^{\circ}\right)\)

Q = PE

Question 29. An electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field the force on it and its potential energy are respectively:

1. 2 q.E and minimum
2. q.E and p.E
3. zero and minimum
4. q.E and maximum

Answer: 3. Zero and minimum

Force on each charge, of dipole

⇒ \(\tilde{F}\)=p E

Total force = zero, they are in the opposite direction

⇒ \(\vec{P}\) and \(\vec{E}\) are parallel to each other

U=\(-\vec{P} \cdot \vec{E}\) is minimum.

Question 30. Some charge is being given to a conductor. Then, its potential:

1. Is maximum at the surface
2. Is maximum at the centre
3. Is the same throughout the conductor
4. Is maximum somewhere between the surface and the

Answer: 3. Is the same throughout the conductor

We know that inside the conductor F = 0.

So, the potential remains the same.

Question 31. The electrostatic force between the metal plates of an isolated parallel plate capacitance C having Q and area A is:

1. proportional to the square root of the distance between the plates.
2. linearly proportional to the distance between the plates.
3. independent of the distance between the plates.
4. inversely proportional to the distance between the plates.

Answer: 3. independent of the distance between the plates.

We know that, For isolated capacitors, Q= constant

⇒ \(F_{\text {plate }}=\frac{Q^2}{2 A \varepsilon_0}\)

So, \(\mathrm{F}\) is independent of the distance between plates.

Question 32. A parallel plate air capacitor has capacity C, distance of separation between plates is d and potential difference V is applied between the plates. The force of attraction between the plates of the parallel plate air capacitor is:

1. \(\frac{C^2 V^2}{2 d}\)
2. \(\frac{C V^2}{2 d}\)
3. \(\frac{C V^2}{d}\)
4. \(\frac{C^2 V^2}{2 d^2}\)

Answer: 2. \(\frac{C V^2}{2 d}\)

According to question,F =\(\frac{Q^2}{2 \varepsilon_0 A} \)

Q =\(C V \text { and } C=\frac{\varepsilon_0 A}{d}\)

⇒ \(\varepsilon_0 A =c d\)

F =\(\frac{C^2 V^2}{2 C d}=\frac{C V^2}{2 d}\)

Question 33. A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an insulating handle. As a result the potential difference between the plates:

1. Increases
2. decreases
3. does not change
4. becomes zero

Answer: 1. Increases

Given

A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an insulating handle.

According to the question

⇒ \(\phi\)= Const and a decrease in C means an increase in V.

C =\(\frac{\varepsilon_0 A}{d}\)

Capacitance =\(\frac{\text { Charge }}{\text { Potential difference }}\)

Potential difference =\(\frac{\text { Charge }}{\text { Capacitance }}\) .

Question 34. A parallel plate capacitor having cross-sectional area A and separation d has air in between the plates. Now an insulating slab of the same area but thickness d/2 is inserted between the plates as shown in the figure having a dielectric constant (K = 4). The ratio of the new capacitance to its original capacitance will be:

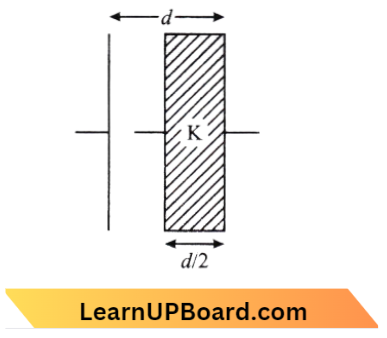
1. 2: 1
2. 8: 5
3. 6: 5
4. 4: 1

Answer: 2. 8: 5

Given

A parallel plate capacitor having cross-sectional area A and separation d has air in between the plates. Now an insulating slab of the same area but thickness d/2 is inserted between the plates as shown in the figure having a dielectric constant (K = 4).

The capacitance of parallel plate capacitor when the medium is air,

⇒ \(C_{\mathrm{o}}=\frac{\varepsilon_0 A}{d}\)

From \(2^{\text {nd }}\) condition,

⇒ \(A^{\prime}=A \cdot t=\frac{d}{2},\) k=4

v \(\mathrm{C}=\frac{\varepsilon_0 A}{(d-t)+\frac{t}{k}}=\frac{\varepsilon_0 \mathrm{~A}}{\left(d-\frac{d}{2}\right)+\frac{d / 2}{4}}\)

= \(\frac{\varepsilon_0 \mathrm{~A}}{\frac{d}{2}+\frac{d}{8}}=\frac{8}{5} \cdot \frac{\varepsilon_0 \mathrm{~A}}{d}\)

⇒ \(\frac{C}{C_0}=\frac{\frac{8}{5} \frac{\varepsilon_0 A}{d}}{\frac{\varepsilon_0 A}{d}}\)

∴ \(\frac{C}{C_0}=\frac{8}{5}\)

Question 35. The capacitance of a parallel plate capacitor with air as a medium is 6 pF. With the introduction of a dielectric medium, the capacitance becomes 30 pF. The permittivity of the medium is: \(\left(\varepsilon_0=8.85 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)\)

1. \(177 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)
2. \(0.44 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)
3. \(5.00 \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)
4. \(0.44 \times 10^{-13} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

Answer: 2. \(0.44 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

Given, \(C_{\mathrm{O}}=6 \mu F\)

⇒ \(C_M=30 \mu \mathrm{F}\)

Dielectric, K=\(\frac{C_M}{C_{\mathrm{O}}}=\frac{30}{6}\)=5

Dermittivity of medium, \(\varepsilon_m =K \times \varepsilon_0=5 \times \varepsilon_0\)

= 5 \(\times 8.854 \times 10^{-12}\)

= \(0.44 \times 10^{-12} \mathrm{C}^2 \mathrm{~N} \mathrm{~m}^{-2}\)

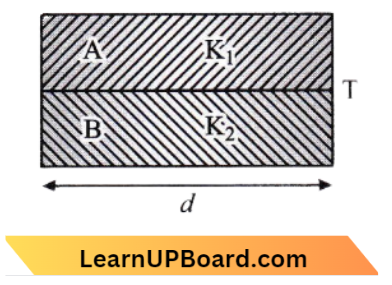
Question 36. Two thin dielectric slabs with dielectric constants K₁ and K₂(K₁ < K₂) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by:

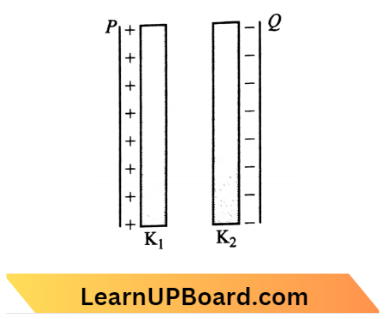
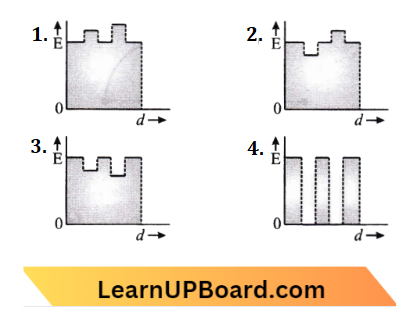
Answer: 2.

Given, the electric field inside the dielectrics will be less than the electric field outside the dielectrics. The electric field inside the dielectric could not be zero. Option (b) is the correct answer.

Question 37. Two parallel metal plates having charge + Q and – Q face each other at a certain distance between them. If the plates are now dipped in the kerosene oil tank, the electric field between the plates will:

1. becomes zero
2. increase
3. decrease
4. remain same

Answer: 3. decrease

Electric field in volume, \(E_0=\frac{\sigma}{2 \varepsilon_0}\)

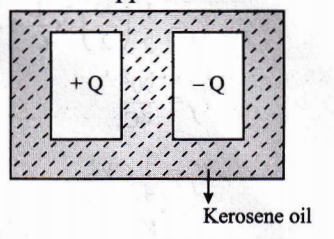
When plates are dipped in a kerosene oil electric field,

Here,E=\(\frac{\sigma}{2 \epsilon_0 \mathrm{~A}}\)

⇒ \(K<E_0\)

So the electric field between the plates will decrease.

Question 38. A parallel plate condenser with oil (dielectric constant 2) between the plates has capacitance C. If oil is removed, the capacitance of the capacitor becomes:

1. \(\sqrt{2 C}\)
2. 2C
3. \(\frac{C}{\sqrt{2}}\)
4. \(\frac{C}{2}\)

Answer: 4. \(\frac{C}{2}\)

We have, the capacitance of a parallel plate capacitor with dielectric (oil) between its plates is

⇒ \(\mathrm{C}=\frac{K \varepsilon_0 A}{d}\) →  Equation 1

where, \(\varepsilon_0\)= electric permittivity of free space

K= dielectric constant of oil

A = Area of each plate of capacitor

d= distance between two plates

When the dielectric (oil) is removed, then, the capacitor’s capacitance will be,

⇒ \(\mathrm{C}_0=\frac{C}{K}=\frac{C}{2}\)  → Equation 2

On comparing Eqs. (1) and (2), we get

⇒ \(C=K C_0 \)

∴ \(C_0=K C_0\)

Question 39. The equivalent capacitance of the combination shown in the figure is:

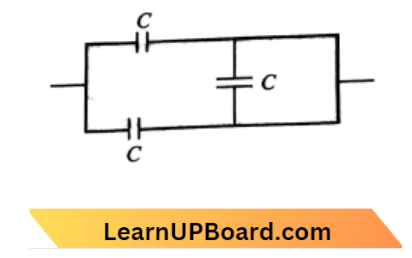
1. 3C
2. 2C
3. \(\frac{C}{2}\)
4. \(\frac{3 C}{2}\)

Answer: 2. 2C

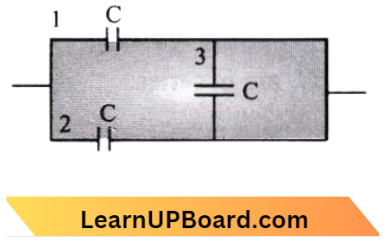
Since the capacitor (3) is shorted out by the parallel wire hence the net capacitance is in parallel.

∴ \(C_{\mathrm{P}}=C+C=2 C\)

Question 40. A parallel-plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constants \(k_1, k_2, k_3, k_4\) as shown in the figure below. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by:

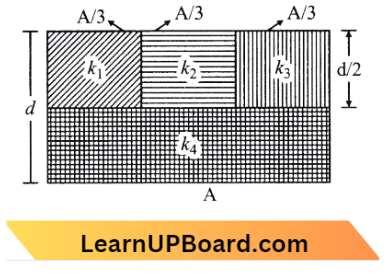
1. \(k=k_1+k_2+k_3+3 k_4\)
2. k=\(\frac{2}{k}\left(k_1+k_2+k_3\right)+2 k_4\)
3. \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)
4. \(\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}=\frac{3}{2 k_4}\)

Answer: 3. \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)

Here the capacitance, C=\(\frac{A k \varepsilon_0}{d}\)

The above three capacitors \(C_1, C_2, C_3\) are in parallel and then it is in series with \(C_4\).

Here, \(C_1=\frac{\left(\frac{A}{3}\right) k_1 \varepsilon_0}{\frac{d}{2}}=\frac{2 k_1}{3 k} C\)

⇒ \(C_2=\frac{\left(\frac{A}{3}\right) k_2 \varepsilon_0}{\frac{d}{2}}=\frac{2 k_2}{3 k} C\)

⇒ \(C_3=\frac{\left(\frac{A}{3}\right) k_3 \varepsilon_0}{\frac{d}{2}}=\frac{2 k_3}{3 k} C \)

⇒ \(C_4=\frac{\left(\frac{A}{3}\right) k_4 \varepsilon_0}{d}=\frac{2 k_4}{k} C\)

Now, the equivalent capacitance for the combination of four capacitors is

or \(\frac{1}{C_{e q}}=\frac{1}{C_1+C_2+C_3}+\frac{1}{C_4}\)

or \(\frac{1}{C}=\frac{3 k}{2 C}\left[\frac{1}{k_1+k_2+k_3}\right]+\frac{k}{2 k_4 C} (as C_{\text {eq }}=\mathrm{C} ) \)

or \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)

Question 41. Three capacitors each of capacitance C and of break-down voltage V are joined in series. The capacitance and breakdown voltage of the combination will be:

1. \(\frac{C}{3}, \frac{V}{3}\)
2. 3 C, \(\frac{V}{3}\)
3. \(\frac{C}{3}\), 3 V
4. 3 C, 3 V

Answer: 3. \(\frac{C}{3}\), 3 V

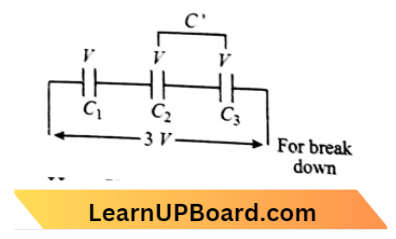
Here V=3 x

⇒ \(C_{e q}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\)

∴ \(C_{e q}=\frac{C}{3}\)

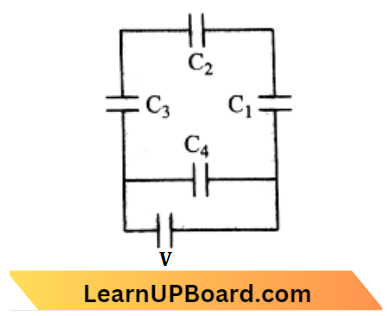
Question 42. A network of four capacitors capacity equal C₁ = C, C2= 2C, C₃ = 3C and C₄= 4C are conducted to a battery as shown in the figure. The ratio of the change on C₂ and C₄.

1. \(\frac{4}{7}\)
2. \(\frac{3}{22}\)
3. \(\frac{7}{4}\)
4. \(\frac{22}{3}\)

Answer: 2. \(\frac{3}{22}\)

Here, \(C_1, C_2, C_3\) are in series.

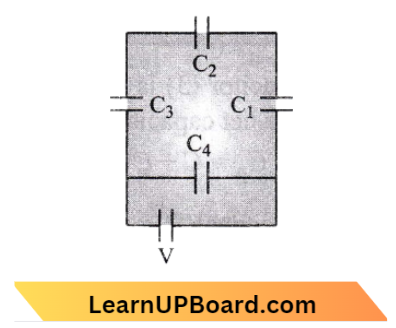
⇒ \(\frac{1}{C^{\prime}}=\frac{1}{C}+\frac{1}{2 C}+\frac{1}{3 C}\)

⇒ \(\frac{1}{C^{\prime}}=\frac{6+3+2}{6 C}=\frac{11}{6 C}\)

⇒ \(C^{\prime \prime}=\frac{6 C}{11}\)

All the capacitors in branch number 1 are in series so the charge on each number capacitor is:

⇒ \(Q^{\prime}=\frac{6}{11} C V\)

Also charge on capacitor \(C_4 is Q=4 \mathrm{~V}\)

Ratio =\(\frac{Q^{\prime}}{Q}=\frac{6 C V}{11 \times 4 C V} \)

= \(\frac{3}{22}\)

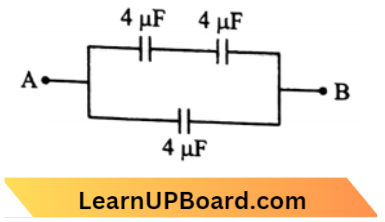
Question 43. Three capacitors each of capacity 4 \(\mu\)F are to be connected in such a way that the effective capacitance is 6 \(\mu\)F. This can be done by:

1. connecting all of them in a series
2. connecting them in parallel
3. connecting two in series and one in parallel
4. connecting two in parallel and one in series

Answer: 3. connecting two in series and one in parallel

⇒ \(\mathrm{C}_{\mathrm{AB}} =(2+4) \mu \mathrm{F}\)

=6 \(\mu \mathrm{F}\)

Question 44. A capacitor of capacitance C₁ charged up to V volt and then connected to an uncharged capacitor C₂. Then, the final potential difference across each capacitor will be:

1. \(\frac{C_2 V}{C_1+C_2}\)
2. \(\frac{C_1 V}{C_1+C_2}\)
3. \(\left(1+\frac{C_2}{C_1}\right) V\)
4. \(\left(1-\frac{C_2}{C_1}\right) V\)

Answer: 2. \(\frac{C_1 V}{C_1+C_2}\)

_⇒ \(V^{\prime}=\frac{C_1 V_1+C_2 V_2}{C_1+C_2}\left( V_2=0\right)\)

∴ \(V^{\prime}=\frac{C_1 V_1}{C_1+C_2}\)

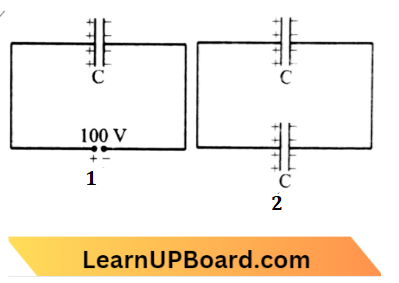
Question 45. A capacitor of capacitance C = 900 pF is charged fully by 100V battery B as shown in figure (1). Then it is disconnected from the battery and connected to another uncharged capacitor of capacitance C = 900 pF as shown in Fig (b). The electrostatic energy stored by the system (2) is:

1. \(4.5 \times 10^{-6} \mathrm{~J}\)
2. 3.25 \(\times 10^{-6} \mathrm{~J}\)
3. 2.25 \(\times 10^{-6} \mathrm{~J}\)
4. 1.5 \(\times 10^{-6} \mathrm{~J}\)

Answer: 3. 2.25 \(\times 10^{-6} \mathrm{~J}\)

Given:

A capacitor of capacitance C = 900 pF is charged fully by 100V battery B as shown in figure (1). Then it is disconnected from the battery and connected to another uncharged capacitor of capacitance C = 900 pF as shown in Fig (b).

⇒ \(\mathrm{V}_1=100 \mathrm{~V}, \mathrm{~V}_2=0 \mathrm{~V}\)

When \(\mathrm{C}_1 and \mathrm{C}_2\) are joined,

V =\(\frac{C_1 V_1+C_2 V_2}{C_1+C_2}\)

= \(\frac{900 \times 100+0}{1800}=50 \mathrm{~V}\)

Energy, U =\(\frac{1}{2}\left(C_1+C_2\right) V^2 \)

= \(\frac{1}{2} \times 1800 \times 10^{-12} \times 50 \times 50\)

= 2.25 \(\times 10^{-6} \mathrm{~J}\)

Question 46. A parallel plate capacitor has a uniform electric field ‘ E ’ in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is: (\(\varepsilon_0\) = permittivity of free space)

1. \(\frac{1}{2} \varepsilon_0 E^2\)
2. \(\varepsilon_0 E A d\)
3. \(\frac{1}{2} \varepsilon_0 E^2 A d\)
4. \(\frac{E^2 A d}{\mathrm{e}_0}\)

Answer: 3. \(\frac{1}{2} \varepsilon_0 E^2 A d\)

Given, Electric Field =E

Distance between plates =d

Area of plates =A

Energy =?

We know, \(\frac{\text { Energy }}{\text { Vol }}=\frac{1}{2} \varepsilon_0 E^2\)

Energy =\(\frac{1}{2} \varepsilon_0 E^2 \times \mathrm{Vol} \)

Energy =\(\frac{1}{2} \varepsilon_0 E^2 \mathrm{Ad}\)

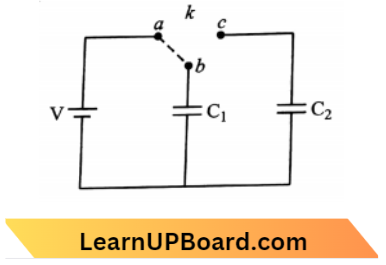
Question 47. Two identical capacitors C₁ and C₂ of equal capacitance are connected as shown in the circuit. Terminals a and b of the key k are connected to charge capacitor C₁ using a battery of emf V volt. Now, disconnecting a and b the terminals b and c are connected. Due to this, what will be the percentage loss of energy?

1. 75%
2. 0%
3. 50%
4. 25%

Answer: 3. 50%

Given

Two identical capacitors C₁ and C₂ of equal capacitance are connected as shown in the circuit. Terminals a and b of the key k are connected to charge capacitor C₁ using a battery of emf V volt.

We know from the question,

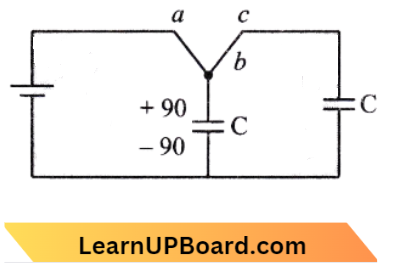
On switching key at point C, \(\frac{90-q}{\mathrm{C}} =\frac{q}{\mathrm{C}}\)

2 q =90

q =\(\left(\frac{90}{2}\right)\)

⇒ \(V_f =\frac{1}{2}\left(\frac{90}{2}\right)^2 \times \frac{1}{C}+\frac{1}{2} \times\left(\frac{90}{2}\right)^2 \times \frac{1}{C}\)

⇒ \(V_f =\frac{90^2}{4 \mathrm{C}}\)

⇒ \(V_f =\frac{1}{4} C V^2\)

⇒ \(\text { Loss }^2 =\frac{V_i-V_f}{V_i} \times 100\)

= \(\frac{\left(\frac{1}{2}-\frac{1}{4}\right) C V^2}{\frac{1}{2} C V^2} \times 100=50 \%\)

Question 48. A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:

1. increases by a factor of 4
2. decreases by a factor of 2
3. remains the same
4. increases by a factor of 2

Answer: 2. decreases by a factor of 2

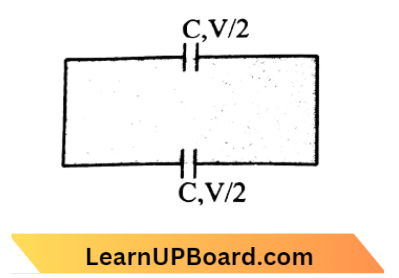
Change An Capacitor, q = CV

When it is connected to another uncharged capacity,

⇒ \(V_C=\frac{q_1+q_2}{C_1+C_2}=\frac{q+0}{C+C}=\frac{V}{2}\)

Initial energy, \(U_i=\frac{1}{2} C V^2\)

Final energy, \(U_f=\frac{1}{2} C\left(\frac{V}{2}\right)^2\)

= \(\frac{1}{2} C\left(\frac{V}{2}\right)^2=\frac{C V^2}{4}\)

Loss of energy, \(U_i-V_f=\frac{C V^2}{4}\)

∴ i.e. decreases by a factor of 2.

Question 49. A capacitor of 2 μF is charged as shown in the figure. When the switch S is turned to position 2, the percentage of its stored energy dissipated is:

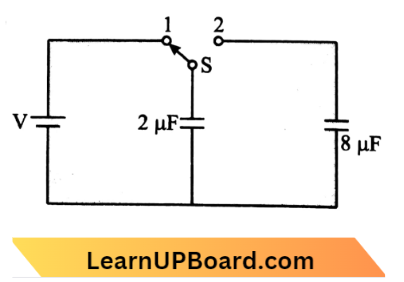
1. 20%
2. 75%
3. 80%
4. 0%

Answer: 3. 80%

First when switch S is connected to point 1. Then,

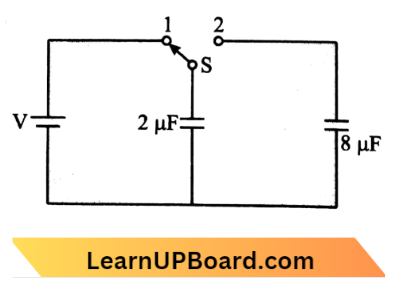
Initial energy stored in capacitor 2 \(\mu \mathrm{F}\) is,

⇒ \(U_i=\frac{1}{2}(2 \mu \mathrm{F}) V^2\left[Q E=\frac{1}{2} C V^2\right]\)

Second when switch S is connected to point 2, then

⇒ \(U_i=\frac{C_1 V_1}{C_1+C_2}=\frac{2 V}{10}=0.2 \mathrm{~V}\)

Final energy in both the capacitors,

⇒ \(\mathrm{U}_f =\frac{1}{2}\left(C_1+C_2\right) V_i^2 \)

=\(\frac{1}{2} \times 10\left(\frac{2 \mathrm{~V}}{10}\right)^2=0.2 \mathrm{~V}^2\)

So, energy dissipated = \(\frac{V^2-0.2 V^2}{V^2} \times 100=80 \%\)

Question 50. A parallel plate air capacitor of capacitance C is connected to a cell of emf V and then disconnected from it. A dielectric slab of electric constant K, which can just fill the air gap of the capacitor, is now inserted in it. Which of the following is incorrect?

1. The potential difference between the plates decreases K times.
2. The energy stored in the capacitor decreases K times.
3. The energy stored in the capacitor decreases K times.
4. The change on the capacitor is not conserved.

Answer: 4. The change on the capacitor is not conserved.

Let charge q on the capacitor (C) when connected to a cell of emf(V) is given by, q = CV

V=\(\frac{q}{C}\)

Energy stored is, U=\(\frac{1}{2} C V^2=\frac{q^2}{2 C}\)

When a dielectric slab of dielectric constant K is inserted, then a new capacitor \(C^{\prime}\) will be

V=\(\frac{q}{C^{\prime}}=\frac{q}{C K}\)

And energy stored is, \(U^{\prime}=\frac{q^2}{2 C K}\)

⇒ \(\Delta U=U-U\)

= \(\frac{q^2}{2 C}\left(\frac{1}{K}-1\right)\)

= \(\frac{1}{2} C V^2\left(\frac{1}{K}-1\right)\)

Question 51. The energy required to charge a parallel plate condenser of plate separation d and plate area of cross-section A such that the uniform electric field between the plates is E is:

1. \(\frac{1}{2} \frac{\varepsilon_0 E^2}{A d}\)
2. \(\frac{\varepsilon_0 E^2}{A d}\)
3. \(\varepsilon_0 E^2 A d\)
4. \(\frac{1}{2} \varepsilon_0 E^2 A d\)

Answer: 3. \(\varepsilon_0 E^2 A d\)

The energy given to the cell, E=\(C V^2\)

Where, C= capacitance of conductor =\(\frac{A \varepsilon_0}{d}\)

V= potential difference across the plate

E =\(\left(\frac{A \varepsilon_0}{d}\right)(E d)^2\)

=A \(\varepsilon_0 E^2 d\)

Question 52. Two condensers, one of capacity C and the other of capacity C/2 are connected to an F-volt battery, as shown. The work done in charging fully both the condensers is:

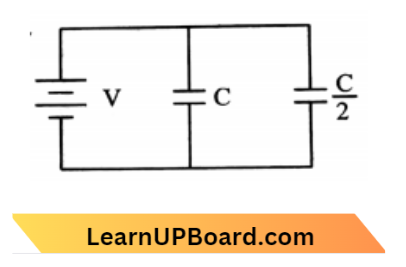
1. \(\frac{1}{4} \mathrm{CV}^2\)
2. \(\frac{3}{4} C V^2\)
3. \(\frac{1}{2} C V^2\)
4. \(2 \mathrm{CV}^2\)

Answer: 2. \(\frac{3}{4} C V^2\)

Work done in charging fully both the condensers,

⇒ \(\mathrm{W}=\mathrm{U}=\frac{1}{2} C V^2+\frac{1}{2}\left(\frac{C}{2}\right) V^2\)

v \(\mathrm{~W}=\mathrm{U}=\frac{3}{4} C V^2\)

Question 53. A capacitor is charged by connecting a battery across its plates. It stores energy U. Now the battery is disconnected and another identical capacitor is connected across it, then the energy stored by both capacitors of the system will be:

1. U
2. \(\frac{U}{2}\)
3. 2U
4. \(\frac{3}{2} U\)

Answer: 2. \(\frac{U}{2}\)

The initial energy held in a capacitor is released when it is charged by connecting a battery across its plates.\(U=\frac{q^2}{2 C}\)

The charge remains constant when the battery is disconnected, i.e. q = constant. Now, another identical capacitor is connected across it, forming a parallel connection. Thus, the equivalent capacitance.

⇒ \(C_{e q} =C_1+C_2 \)

=C+C=2 C

Final energy stored by the system of capacitors,

⇒ \(U^{\prime}=\frac{q^2}{2 C_{\mathrm{eq}}}\)

⇒ \(U^{\prime}=\frac{q^2}{2(2 \mathrm{C})}\)

⇒ \(U^{\prime}=\frac{1}{2} U \)

∴ \(U^{\prime}=\frac{1}{2} U\)

Question 54. If the potential of a capacitor having a capacity of 6μF is increased from 10 V to 20 V, then the increase in its energy will be:

1. 4 \(\times 10^{-4} \mathrm{~J}\)
2. 4 \(\times 10^{-4} \mathrm{~J}\)
3. 9 \(\times 10^{-4} \mathrm{~J}\)
4. 12 \(\times 10^{-4} \mathrm{~J}\)

Answer: 3. 9 \(\times 10^{-4} \mathrm{~J}\)

Energy is stored in the dielectric medium between the plates of a charged capacitor in the form of electric field energy. The energy stored in the capacitor is determined by \(U=\frac{1}{2} C V^2\)

If the initial and the final potential are \(v_1 v_2\) respectively,

then increase in energy \((\Delta U)\),

⇒ \(\Delta U =\frac{1}{2} C\left(C_2^2-V_1^2\right)\)

= \(\frac{1}{2} \times(6 \times 10^{-6}) \times[(20)^2-(10^2]\)

= \(\frac{1}{2}\left(3 \times 10^{-6}\right) \times 300=9 \times 10^{-4} \mathrm{~J}\)

NEET Physics For Electric Charges And Field Multiple Choice Questions

Question 1. Two point charges A and B having charges + Q and – Q respectively, are placed at a certain distance apart and force acting between them in F. If 25% of charges of A is transferred to B, then the force between the charges becomes

1. \(\frac{9 F}{16}\)
2. \(\frac{16 F}{9}\)
3. \(\frac{4 F}{3}\)
4. F

Answer: 1. \(\frac{9 F}{16}\)

We can write from the given question,

Two point charges A and B having charges + Q and – Q respectively, are placed at a certain distance apart and force acting between them in F. If 25% of charges of A is transferred to B

F= \(k \frac{Q^2}{r^2}\)

If 25% of the charge of A transferred to B then,

⇒ \(q_{\mathrm{A}}=Q-\frac{Q}{4}=\frac{3 Q}{4}\)

and \(q_B=-Q+\frac{Q}{9}=\frac{-3 q}{4}\)

⇒ \(F_1=\frac{K q_{\mathrm{A}} q_{\mathrm{B}}}{r^2}\)

⇒ \(F_1=\frac{K\left(\frac{3 Q}{4}\right)^2}{r^2}=\frac{9}{16} \frac{K Q}{r^2}\)

∴ \(F_1=\frac{9 F}{16}\) .

Question 2. Suppose the charge of a proton and an electron differ slightly. One of them is e and the other is (e + Δe). If the net electrostatic force and the gravitational force between two hydrogen atoms placed at a distance d (much greater than atomic size) apart are zero, then Ae is of the order [Given the mass of hydrogen if, m_h = 1.67 x 10^-27 kg]:

1. 10^-20C
2. 10^-23C
3. 10^-37C
4. 10^-47C

Answer: 3. 10^-37C

Read and Learn More NEET Physics MCQs

Here gravitational attractive force between two H-atoms is \(F_G=\frac{G m^2}{d^2}\)  → Equation 1

and electrostatic repulsive force between two H-atom is \(F_e=\frac{K q^2}{d^2}=\frac{K(\Delta e)^2}{d^2}\) →  Equation 2

Thus we have, \(\frac{K(\Delta e)^2}{d^2}=\frac{G m^2}{d^2}\)

⇒ \(9 \times 10^9(\Delta e)^2=6.67 \times 10^{-11} \times 1.67 \times 10^{-27} \times 1.67 \times 10^{-27}\)

⇒ \((\Delta e)^2=\frac{6.67 \times 1.67 \times 1.07}{9} \times 10^{-74}\)

∴ \(\Delta e=1.437 \times 10^{-37} \mathrm{C}\)

Question 3. Two identical charged spheres suspended from a common point by two massless strings of lengths /, are initially at a distance d (d < 1) apart because of their mutual repulsion. The charges begin to leak from both spheres at a constant rate. As a result, the spheres approach each other with a velocity v. Then, v varies as a function of the distance x between the spheres, as:

1. v \(\propto x^{-1 / 2}\)
2. v \(\propto x^{-1}\)
3. v \(\propto x^{-1}\)
4. v \(\propto x^{1 / 2}\)

Answer: 2. v \(\propto x^{-1}\)

From the diagram,

⇒ \(\tan \theta=\frac{F_e}{m g}=\theta\)

⇒ \(\frac{K q^2}{x^2 m g}=\frac{x}{2 l}\)

or \(x^3 \propto q^2\) →  Equation 1

or \(x^{3 / 2} \propto q\) →  Equation 2

differential eq. (1) w.r.t. to time,

⇒ \(3 x^2 \frac{d x}{d t} \propto 2 q \frac{d q}{d t}\)

but \(\frac{d q}{d t}\) is constant.

So \(x^2(v) \propto q \)replace q from eq. (2),

⇒ \(x^2(v) \propto x^{3/2}\)

∴ \(v \propto x^{+1 / 2}\)

Question 4. Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly damped at half the height. The equilibrium separation between the balls now becomes.

1. \(\left(\frac{1}{\sqrt{2}}\right)^2\)
2. \(\left(\frac{r}{\sqrt[3]{2}}\right)\)
3. \(\left(\frac{2 r}{\sqrt{3}}\right)\)
4. \(\left(\frac{2 r}{3}\right)\)

Answer: 2. \(\left(\frac{r}{\sqrt[3]{2}}\right)\)

Given

Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly damped at half the height.

Here, \(\tan \theta =\frac{F}{m g}\)

⇒ \(\frac{r}{y} =\frac{k q^2}{r^2 m g}\)

⇒ \(y \propto r^3\)

⇒ \(\left(\frac{r^1}{r}\right)^3=\frac{y / 2}{y}\)

∴ \(r^1=r\left(\frac{1}{2}\right)^{1 / 3}\)

Question 5. A charge ‘q’ is placed at the centre of the line joining two equal charges ‘Q. The system of three charges will be in equilibrium if ‘q’ is equal to:

1. -S/4
2. g/4
3. – e/2
4. e/2

Answer: 1. -S/4

According to the question,

for equilibrium, the net force on charge p = 0

⇒ \(\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{Q} q}{r^2}+\frac{1}{4 \pi \epsilon_0} \cdot\)

⇒ \(\frac{\mathrm{Q}^2}{\left(\frac{r}{2}\right)^2}\)=0

⇒ \(\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{Q}^2}{r^2} =-\frac{1}{4 \pi \epsilon_0} \frac{4 \mathrm{Q} q}{r^2}\)

Q=-4 q

q = \(-\frac{Q}{4}\)

Question 6. Two positive ions, each carrying a charge q, are separated by a distance d. If F is the force of repulsion between the ions, the number of electrons missing from each ion will be (e being the charge on an electron):

1. \(\frac{4 \pi \varepsilon_0 F d^2}{e^2}\)
2. \(\sqrt{\frac{4 \pi \varepsilon_0 F e^2}{d^2}}\)
3. \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)
4. \(\frac{4 \pi \varepsilon_0 F d^2}{q^2}\)

Answer: 3. \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)

Given

Two positive ions, each carrying a charge q, are separated by a distance d. If F is the force of repulsion between the ions,

The force of repulsion between them is,

F=\(k \frac{q q}{d^2}=\frac{1}{4 \pi \varepsilon_0} \frac{q q}{d^2}\)  → Equation 1

Here, q = ne

F= \(\frac{1}{4 \pi \varepsilon_0} \frac{(n e)(n e)}{d^2}\)

n= \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)

Question 7. The unit of permittivity of free space ε₀ is:

1. coulomb/newton-metre
2. newton-metre2/coulomb²
3. coulomb²/newton-metre²
4. coulomb²/(newton-metre)²

Answer: 3. coulomb²/newton-metre²

We know that, F =\(\frac{1}{4 \pi \varepsilon_0} \frac{q^2}{r^2}\)

∴ \(\varepsilon_0 =\frac{1}{4 \pi} \frac{a^2}{\mathrm{Fr} r^2}=\frac{\mathrm{C}^2}{\mathrm{~N}-\mathrm{m}^2}\)

Question 8. An electron is moving around the nucleus of a hydrogen atom in a circular orbit of radius r. The coulomb force \(\vec{F}\) between the two is \(\left(\text { where } K=\frac{1}{4 \pi \varepsilon_0}\right)\):

1. \(K \frac{e^2}{r^2} \hat{r}\)
2. -K \(\frac{e^2}{r^3} \hat{r}\)
3. -K \(\frac{e^2}{r^2} \hat{r}\)
4. K \(\frac{e^2}{r^3} \hat{r}\)

Answer: 4. K \(\frac{e^2}{r^3} \hat{r}\)

The charge on hydrogen nuclear \(q_1=+v e \)

Coulomb’s force, F =\( K \frac{q_1 q_2}{r^2}\)

= K \(\frac{(+e)(-e)}{r^2} \hat{r}=-\frac{k e^2}{r^2} \hat{r}\)

Question 9. When air is replaced by a dielectric medium of constant k, the maximum force of attraction between two charges, separated by a distance

1. decreases K times
2. increases AT times
3. remains uncharged
4. becomes – times

Answer: 1. decreases K times

According to Coulomb’s law, the force between two charges is directly proportional to the product of charges and inversely proportional to the square of the distance between them.

F=\(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)  → Equation 1

Where, \(\frac{1}{4 \pi \varepsilon_0}\) = proportionality constant

If a dielectric medium of constant K is placed between them, then, a new force between the charges will be,

⇒ \(F_1=\frac{1}{4 \pi \varepsilon_0 K} \frac{q_1 q_2}{r^2}\) →  Equation 2

Dividing Eq. (2) by (1), we get,

⇒ \(\frac{F_1}{F}=\frac{1}{k}\)

⇒ \(F^{\prime}=\frac{F}{k}\)

∴ Thus, the new force decreases K times.

Question 10. An electron falls from rest through a vertical distance h in a uniform and vertically upward-directed electric field E. The direction of the electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall of the proton is:

1. 10 times greater
2. 5 times greater
3. smaller
4. equal

Answer: 3. smaller

Given

An electron falls from rest through a vertical distance h in a uniform and vertically upward-directed electric field E. The direction of the electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h.

Consider, the force on a charged particle in an electric field is: F = qE

And from Newton’s 2 \( { }^{\text {nd }}\) law of motion,

F = ma

From the above two equations,

qE = ma

a =\(\frac{q E}{m}\)  → Equation 1

Now consider that particle falls from rest means u=0 and s=h

S= \(u t+a t^2 \)

h= \(\frac{1}{2} a t^2\)

h= \(\frac{1}{2}\left(\frac{q E}{m}\right)^{t^2}\)

h= \(\frac{1}{2} \frac{q E}{m} t^2\)

t= \(\sqrt{\frac{2 h m}{q E}}\)

Question 11. The electric field in a certain region is acting radially outward and is given by E = Ar. A charge contained in a sphere of radius ‘a’ centred at the origin of the field’ will be given by:

1. \(4 \pi \varepsilon_0 A a^2\)
2. A \(\varepsilon_0 a^2\)
3. 4 \(\pi \varepsilon_0 A a^3\)
4. \(\varepsilon_0 A a^3\)

Answer: 3. 4 \(\pi \varepsilon_0 A a^3\)

From eq.(1)\( t \propto \sqrt{m}\) a q is the same for electron and proton.

Since an electron has a smaller mass it will take less time.

Question 12. The electric field at a distance \(\frac{3 R}{2}\) from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance \(\frac{R}{2}\) from the centre of the sphere is:

1. zero
2. E
3. \(\frac{E}{2}\)
4. \(\frac{E}{3}\)

Answer: 1. zero

We know that the electric field inside the conductor is zero. So, the electric field at a distance \(\frac{R}{2}\) from the centre of the sphere will also be zero.

Question 13. A particle of mass m and charge q is placed at rest in a uniform electric field E and then released. The kinetic energy attained by the particle after moving a distance y is:

1. \(q E y^2\)
2. \(q E^2 y\)
3. \(q E y\)
4. \(q^2 E y\)

Answer: 3. \(q E y\)

We have, electric force on a charged particle, F = qE

Mechanical on a charged particle in a uniform electric field is, F = ma = Eq

a = \(\frac{q E}{m}\)

From the equation of motion, we get,

⇒ \(v^2 =u^2+2 a y \)

a =\(\frac{q E}{m}\)

= \(\frac{2 q E \mathrm{y}}{m}\)

⇒ \(\ldots[\mathrm{u}=0]\)

Now, kinetic energy of the particle, k =\(\frac{1}{2} m v^2 \)

= \(\frac{m}{2} \times \frac{2 q E \mathrm{y}}{m}=q E y\)

Question 14. A square surface of side Z metre in the plane of the paper is placed in a uniform electric field E (volt/m) acting along the same place at an angle θ with the horizontal side of the square as shown in the figure. The electric flux linked to the surface in a unit of V-m is

1. \(E L^2\)
2. \(E L^2 \cos \theta\)
3. \(E L^2 \sin \theta\)
4. 0

Answer: 4. 0

Given

A square surface of side Z metre in the plane of the paper is placed in a uniform electric field E (volt/m) acting along the same place at an angle θ with the horizontal side of the square as shown in the figure.

We know that, flux, \(\phi =\vec{E} \cdot \vec{A}\)

= E A \(\cos \theta=\vec{E} \cdot \vec{A}\)

And \(\vec{E} \cdot \vec{A}\)=0 then lines are parallel to the surface.

Question 15. A square surface of side L metres is in the plane of the paper. A uniform electric field \(\vec{E}\)(volt/m), also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in SI units associated with the surface is:

1. \(E L^2\)
2. \(E L^2 / 2 \varepsilon_{\mathrm{o}}\)
3. \(E L^{2 / 2}\)
4. zero

Answer: 4. zero

Given

A square surface of side L metres is in the plane of the paper. A uniform electric field \(\vec{E}\)(volt/m), also in the plane of the paper, is limited only to the lower half of the square surface

Electric flux \(\phi_E =\int \vec{E} \cdot \overrightarrow{d s}=\int E d s \cos \theta\)

= \(\int E d s \cos 90^{\circ}\)=0

Question 16. Two point charges -q and +q are placed at a distance of L, as shown in the figure. The magnitude of electric field intensity at a distance R (R > >L) varies as:

1. \(\frac{1}{\mathrm{R}^2}\)
2. \(\frac{1}{\mathrm{R}^3}\)
3. \(\frac{1}{\mathrm{R}^4}\)
4. \(\frac{1}{\mathrm{R}^6}\)

Answer: 2. \(\frac{1}{\mathrm{R}^3}\)

The electric field due to a dipole at any arbitrary point (R, Q) is

⇒ \(\mathrm{E}=\frac{p}{4 \pi \varepsilon_0 R^3} \sqrt{3 \cos ^2 \theta+1}\)

⇒ \(\mathrm{E} \propto \frac{1}{\mathrm{R}^3}\) .

∴ Here, \(\mathrm{E} \propto \frac{1}{\mathrm{R}^3}\).

Question 17. Polar molecules are the molecules:

1. having zero dipole moment.
2. acquire a dipole moment only in the presence of an electric field due to the displacement of charges.
3. acquire a dipole moment only when the magnetic field is absent.
4. having a permanent electric dipole moment.

Answer: 4. having a permanent electric dipole moment.

Polar molecules are molecules having a permanent electric dipole moment.

Question 18. The electric field at a point on the equatorial plane at a distance r from the centre of a dipole having dipole moment P is given by (r > > separation of two charges forming the dipole \(\varepsilon_0\) = permittivity of free space):

1. \(\frac{-P}{4 \pi \varepsilon_0 r^3}\)
2. \(\frac{2 P}{4 \pi \varepsilon_0 r^3}\)
3. \(-\frac{P}{4 \pi \varepsilon_0 r^2}\)
4. \(\frac{P}{4 \pi \varepsilon_0 r^2}\)

Answer: 1. \(\frac{-P}{4 \pi \varepsilon_0 r^3}\)

Electric field due to an electric dipole at an equatorial plane at a distance r from the centre of the dipole is given by:

⇒ \(E_e=\frac{q(2 a)}{4 \pi \varepsilon_0\left(r^2+a^2\right)^{3 / 2}}\)

Directed from Q to R,

⇒ \(E_e=-\frac{P}{4 \pi \varepsilon_0\left(r^2+a^2\right)^{\frac{3}{2}}}\)

For a very short dipole (a < < r),

∴ \(E_e=-\frac{P}{4 \pi \varepsilon_0 r^3}\)

Question 19. Three point charges +q, -2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0, y = 0, z = 0) and (x = a, y = 0, z = 0) respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are:

1. \(\sqrt{2}\) q a along the line joining points (x=0, y=0, z=0) and (x=a, y=a, z=0)
2. q a along the line joining points (x=0, y=0, z=0) and (x=a, y=a, z=0)
3. \(\sqrt{2}\) q a along +x direction
4. \(\sqrt{2}\) q a along +y direction

Answer: 1. \(\sqrt{2}\) q a along the line joining points (x=0, y=0, z=0) and (x=a, y=a, z=0)

This consists of two dipoles, – q and +4 with dipole moment along with the +y direction and q and +q along the X-direction.

The resultant moment ,=\(\sqrt{q^2 a^2+q^2 a^2}\) = \(\sqrt{2} q a\)

Along the direction 45″ that is along OP where P is (+a, a,0)

Question 20. The formation of the dipole is due to two equal and dissimilar point charges placed at a:

1. short distance
2. long distance
3. above each other
4. None of these

Answer: 1. short distance

A pair of equal and opposite point charges separated by a small distance form an electric dipole. Electric dipoles are atoms or molecules of ammonia, water alcohol, carbon dioxide, HCl, and other compounds in which the centres of positive and negative charge distributions are separated by a small distance

Question 21. The intensity of an electric field (E) depends on distance r due to a dipole, is related to:

1. E\( \propto \frac{1}{r}\)
2. E \(\propto \frac{1}{r^2}\)
3. E \(\propto \frac{1}{r^3}\)
4. E \(\propto \frac{1}{r^4}\)

Answer: 3. E \(\propto \frac{1}{r^3}\)

On the axial line of an electric dipole, the field intensity is given by E=\(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 p}{r^3}\)  → Equation 1

Electric field at equatorial position, E=\(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{p}{r^3}\) →  Equation 2

where. p is electric dipole moment,

From (1) and (2), we get E \(\propto \frac{1}{\mathrm{r}^3}\)

Question 22. An electric dipole is placed at an angle of 30° with an electric field intensity of 2 x 10⁵ N/C. It experiences a torque equal to 4 Nm. The charge on the dipole. If the dipole length is 2 cm is:

1. 8 mC
2. 2 mC
3. 5 mC
4. 7μC

Answer: 2. 2 mC

We know that the Torque in an electric dipole is

⇒ \(\vec{\tau}=\vec{P} \times \vec{E}\)

⇒ \(|\tau| =P E \sin \theta\)

We can write, \(\tau=q 2 l E \sin \theta=q \times 2 l \times E \sin \theta\)

putting the given values we have, 4 =q \(\times 2 \times 2 \times 10^{-4} \times 2 \times 10^5 \times \sin 30^{\circ}\)

q =2 \(\times 10^{-3} \mathrm{C}=2 \mathrm{mC}\)

Question 23. A spherical conductor of radius 10 cm has a charge of 3.2 x 10^-7 distributed uniformly. What is the magnitude of the electric field at a point 15 cm from the centre of the Sphere \(\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\)

1. \(1.28 \times 10^5 \mathrm{~N} / \mathrm{C}\)
2. 1.28 \(\times 10^6 \mathrm{~N} / \mathrm{C}\)
3. 1.28 \(\times 10^7 \mathrm{~N} / \mathrm{C}\)
4. 1.28 \(\times 10^4 \mathrm{~N} / \mathrm{C}\)

Answer: 1. \(1.28 \times 10^5 \mathrm{~N} / \mathrm{C}\)

Given: r=10 \(\mathrm{~cm}=10 \times 10^{-2} \mathrm{~m}\)

Charge, q=3.2 \(\times 10^{-7} \mathrm{C}\)

The electric field at a point (x=15 cm ) from the centre of the sphere is:

⇒ \(\mathrm{E} =\frac{1}{4 \pi \varepsilon_0} \frac{q}{x^2}\)

= \(9 \times 10^9 \times \frac{3.2 \times 10^{-7}}{225 \times 10^{-4}}\)

= \(1.28 \times 10^5 \mathrm{~N} / \mathrm{C}\) .

Question 24. A thin conducting ring of radius R is given a charge + Q. The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on the part ACDB of the ring is:

1. 3 E along KO
2. 3 along OK
3. E along KO
4. 3 E along OK

Answer: 2. 3 along OK

The electric field due to the given charged ring is zero at centre O. So electric field due to AKB is equal and opposite to the electric field due to ACDB, from the principle of superposition. Since \(\overrightarrow{\mathrm{E}}\) is field strength, of O along \(\overrightarrow{K O}\) . So electric field strength due to ACDB along \(\overrightarrow{O K}\) and it is equal to E.

Question 25. The electric field strength in air at NTP is 3 x 10⁸ V/m. The maximum charge that can be given to a spherical conductor of radius 3 m is:

1. 3 x 10⁴ C
2. 3 x 10^-3 C
3. 3 x 10^-2 C
4. 3 x 10^-1 C

Answer: 2. 3 x 10^-3 C

Given, \(E_{\max }=3 \times 10^6 \mathrm{~V} / \mathrm{m}\) and R=3 \(\mathrm{~m}\) We have,

E =\(\frac{1}{4 \pi \varepsilon_0} \times \frac{Q}{R^2}\)

⇒ \(Q_{\max } =4 \pi \varepsilon_0 R^2 E_{\max }\)

=\(\frac{3 \times 3 \times 3 \times 10^6}{9 \times 10^9}\)

=3 \(\times 10^{-3} \mathrm{C}\)

Question 26. Two spherical conductors A and B of radii 1 mm and 2 mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is:

1. 4:1
2. 1:2
3. 2:1
4. 1:4

Answer: 1. 4:1

When a conducting wire connects two conducting spheres, charge flows from one sphere (with a higher potential) to the other (with a lower potential) until both spheres have the same potential.

E=\(\frac{1}{4 \pi \varepsilon_0} \times \frac{q}{r^2}\)

So, for different cases, \(\frac{E_1}{E_2}=\left(\frac{r_2}{r_1}\right)^2\)=4: 1

Question 27. A sphere encloses an electric dipole with charge \(\pm 3 \times 10^{-6} \mathrm{C}\). What is the total electric flux across the sphere?

1. \(-3 \times 10^{-6} \mathrm{~N}-\mathrm{m}^2 / \mathrm{C}\)
2. zero
3. \(3 \times 10^6 \mathrm{~N}-\mathrm{m}^2 / \mathrm{C}\)
4. \(6 \times 10^{-6} \mathrm{~N}-\mathrm{m}^2 / \mathrm{C}\)

Answer: 2. zero

From the figure it is clear that the sphere is enclosed a change is q= \(\pm 3 \times 10^{-6} \mathrm{C}\) which means it is a dipole.

We know that,Flux, \(\phi=\frac{(\text { Charge })_{\text {inside }}}{\epsilon_0}=\frac{q_{\text {in }}}{\epsilon_0}\)

Here total charge inside the sphere is zero.

⇒ \(\phi=\frac{0}{\epsilon_0}\)=0

The charge enclosed is zero.

The total electric flux is zero.

Question 28. A charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, then the outward electric flux will:

1. be reduced to half
2. remain the same
3. be doubled
4. increases four times

Answer: 2. remain the same

⇒ \(\phi_{\text {net }}=\frac{\Sigma q}{\varepsilon_0}\)

Net flux does not depend on the size of the Gaussian surface.

So, Flux remain unchanged

Question 29. A hollow cylinder has a charge q coulomb within it. If \(\phi\) is the electric flux in units of voltmeter associated with the curved surface B, the flux linked with the plane surface A in units of voltmeter will be:

1. \(\frac{q}{2 \varepsilon_0}\)
2. \(\frac{\phi}{3}\)
3. \(\frac{q}{\varepsilon_0}-\phi\)
4. \(\frac{1}{2}\left(\frac{q}{\varepsilon_0}-\phi\right)\)

Answer: 4. \(\frac{1}{2}\left(\frac{q}{\varepsilon_0}-\phi\right)\)

Let \(\phi_A, \phi_B\) and \(\phi_C\) be the electric fuse linked with A, B and C.

According to Gauss theorem, \(\phi_{\mathrm{A}}+\phi_{\mathrm{B}}+\phi_{\mathrm{C}}=\frac{q}{\varepsilon_0}\)

since, \(\phi_{\mathrm{A}}=\phi_{\mathrm{C}}\)

2 \(\phi_{\mathrm{A}}+\phi_{\mathrm{B}}=\frac{q}{\varepsilon_0}\)

or \(2 \phi_{\mathrm{A}}=\frac{q}{\varepsilon_0}-\phi_{\mathrm{B}}\)

or \(2 \phi_{\mathrm{A}}=\frac{q}{\varepsilon_0}-\phi \quad\left\{\text { since } \phi_{\mathrm{B}}=\phi\right\}\)

Question 30. A charge q is located at the centre of a cube. The electric flux through any face is:

1. \(\frac{2 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)
2. \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)
3. \(\frac{\pi q}{6\left(4 \pi \varepsilon_0\right)}\)
4. \(\frac{-q}{6\left(4 \pi \varepsilon_0\right)}\)

Answer: 2. \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)

The electric flux through any face,

⇒ \(\phi_{\text {face }}=\frac{q}{\varepsilon_0}\)

= \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)

Question 31. A Charge q is placed at the corner of a cube of side a. The electric flux through the cube is:

1. \(\frac{q}{\varepsilon_0}\)
2. \(\frac{q}{3 \varepsilon_0}\)
3. \(\frac{q}{6 \varepsilon_0}\)
4. \(\frac{q}{8 \varepsilon_0}\)

Answer: 4. \(\frac{q}{8 \varepsilon_0}\)

According to Gauss law, the electric flux through a closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed by the surface.

since, q is the charge enclosed by the surface, then electric flux,q= \(\phi=\frac{1}{\varepsilon_0}\)

If charge q is placed in one of the cube’s corners, it will be divided into eight similar cubes.

Therefore, electric flux through the cube \(\phi^{\prime}=\frac{1}{8}\left(\frac{q}{\varepsilon_0}\right)\)

Question 32. A point charge + q is placed at the mid-point of a cube of side L. The electric flux emerging from the cube is:

1. \(\frac{q}{\varepsilon_0}\)
2. \(\frac{6 q L^2}{\varepsilon_0}\)
3. \(\frac{q}{6 L^2 \varepsilon_0}\)
4. zero

Answer: 1. \(\frac{q}{\varepsilon_0}\)

According to Gauss’s theorem, the total electric flux over a closed surface is \(\frac{1}{\varepsilon_0}\) times the total charges contained inside the surface.

Total electric flux =\(\frac{\text { Total charge inside cube }}{\varepsilon_0}\)

∴ \(\phi =\frac{\mathrm{q}}{\varepsilon_0}\)

Question 33. Two parallel infinite line charges with linear charge densities + \(\lambda\) C/m and – \(\lambda\), C/m is placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?

1. \(\frac{2 \lambda}{2 \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)
2. \(\frac{\lambda}{\pi \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)
3. \(\frac{\lambda}{2 \pi \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)
4. Zero

Answer: 2. \(\frac{\lambda}{\pi \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)

Electric field due to line charge (1), \(\vec{E}_1=\frac{\lambda}{2 \pi \varepsilon_0 R} \hat{i}\)

Electric field due to line charge (2),

⇒ \(\vec{E}_2 =\frac{\lambda}{2 \pi \varepsilon_0 R} \hat{i} \mathrm{~N} / \mathrm{C}\)

⇒ \(E_{\text {net }} =\vec{E}_1+\vec{E}_2\)

= \(\frac{\lambda}{2 \pi \varepsilon_0 \mathrm{R}} i+\frac{\lambda}{2 \pi \varepsilon_0 \mathrm{R}} \hat{i}\)

= \(\frac{\lambda}{\pi \varepsilon_0 \mathrm{R}} \hat{i} \mathrm{~N} / \mathrm{C}\)

Question 34. A hollow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:

1. zero as increases for r < R_i decreases as r increases for r > R
2. zero as r increases for r < rR_i increases as r increases for r > R
3. decreases as r increases for r < R and for r > R
4. increases as r increases for r < R and for r > R

Answer: 1. Zero as increases for r < Ri decreases as r increases for r > R

Charge Q will be distributed over the surface of a hollow metal sphere.

(1) For \(\mathrm{r}<\mathrm{R}(inside)\)

By gauss law \(\oint \overrightarrow{E_{1 \mathrm{n}}} \cdot \overrightarrow{d \mathrm{~s}}=\frac{q_{e n}}{\varepsilon_0}\)

∴ \(E_{\text {in }}=0 (q_{\text {en }}=0)\)

(2) For r>R (outside)

⇒ \(\oint \vec{E}_0 \cdot \overrightarrow{d s}=\frac{q_{e n}}{\varepsilon_0}\)

Here \(q_{\text {en }}\)=0

⇒ \(\left(q_{e n}=\mathrm{Q}\right)\)

For \(r>R,\vec{E}_0=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{\left|\vec{R}^2\right|} \hat{r}\)

⇒ \(E_0 \propto \frac{1}{r^2}\)

∴ \(\vec{E}_0\) decreases

NEET Physics For Waves Multiple Choice Questions

Question 1. Which one of the following statements is true?

1. Both light and sound waves can travel in a vacuum
2. Both light and sound waves in air are transverse
3. The sound waves in air are longitudinal while the light waves are transverse
4. Both light and sound waves in air are longitudinal

Answer: 3. The sound waves in air are longitudinal while the light waves are transverse

The sound waves in air are longitudinal while the light waves are transverse

Question 2. A wave travelling in the positive x-direction having displacement along 7-direction as 1 m, wavelength \(2 \pi \mathrm{m}\) and frequency of \(\frac{1}{\pi} H z\) is represented by:

1. \(y=\sin (x-2 t)\)
2. \(y=\sin (2 \pi x-2 \pi t)\)
3. \(y=\sin (10 \pi x-20 \pi t)\)
4. \(y=\sin (2 \pi \mathrm{x}-2 \pi t)\)

Answer: 1. \(y=\sin (x-2 t)\)

Given

A wave travelling in the positive x-direction having displacement along 7-direction as 1 m, wavelength \(2 \pi \mathrm{m}\)

According to Question, A =\(1 \mathrm{~m} \)

y =A \(\sin (k x-\omega t)\)

= \(\sin \left(\frac{2 \pi}{2 \pi} x-2 \pi \times \frac{1}{\pi} t\right)\)

= \(\sin (x-2 t)\)

Question 3. Two waves are represented by the equations \(y_1=a \sin (\omega t+k x+0.57) \mathrm{m}\) and \(y_2=a \cos (\omega t+k x) \mathrm{m}\), where x in metre and t in second. The phase difference between them is:

1. 1.25 rad
2. 0.57 rad
3. 1.57 rad
4. 1.0 rad

Answer: 4. 1.0 rad

It is given that, \(y_1=A \sin (\omega t+k x+0.57) \mathrm{m}\)  →  Equation 1

and \(y_2=A \cos (\omega t+k x) \mathrm{m}\)

⇒ \(y_2=A \sin \left(\frac{\pi}{2}+\omega t+k x\right) \mathrm{m}\)  → Equation 2

Thus from these two equations, \(\Delta \phi =\phi_2-\phi_1\)

= \(\frac{\pi}{2}-0.57\)

=1.57-0.57=1 \(\mathrm{rad}\)

Read and Learn More NEET Physics MCQs

Question 4. A wave in a string has an amplitude of 2 cm. The wave travels in the + x direction with a speed of 128 ms^-1 and it is noted that 5 complete waves fit in the 4 m length of the string. The equation describing the wave is:

1. y= (0.02)m sin(7.85x + 1005t)
2. y = (0.02)m sin (15.7x- 2010t)
3. y = (0.02)m sin(15.7x + 2010t)
4. y = (0.02)m sin (7.85x + 1005t)

Answer: 4. 7 = (0.02)m sin (7.85x + 1005t)

Given

A wave in a string has an amplitude of 2 cm. The wave travels in the + x direction with a speed of 128 ms^-1 and it is noted that 5 complete waves fit in the 4 m length of the string.

According to the question, A =2 \(\mathrm{~cm}\) and

Direction  =+x direction

v =128 \(\mathrm{~ms}^{-1}\)

k =\(\frac{2 \pi}{\lambda}=\frac{2 \pi \times 5}{4}=7.85\)

And v =\(\frac{\omega}{k}=128 \mathrm{~ms}^{-1}\)

⇒ \(\omega =v \times k=128 \times 7.85=1005\)

y =\(A \sin (k x-\omega t) \)

becomes y =2 \(\sin (7.85 x-1005 t)\)

= (0.02) m \(\sin (7.85 x-1005 t)\)

Question 5. The wave described by y = \(y=0.25 \sin (10 \pi x-2 \pi t)\), where x and y are in metres and t in second, is a wave travelling along the:

1. – ve x – direction with frequency 1 Hz
2. + ve x – direction with frequency π Hz and wavelength λ = 0.2m
3. + ve x – direction with frequency 1 Hz and wavelength λ = 0.2 m
4. + ve x – direction with amplitude 0.25 m and wavelength λ = 0.2 m

Answer: 3. + ve x – direction with frequency 1 Hz and wavelength A = 0.2 m

Given,  y=0.25\( \sin (10 \pi x-2 \pi t)\)

comparing with equation of wave, y =A \(\sin (k x-\omega t)\)

A=0.25, k =10\( \pi, \omega=2 \pi\)

⇒ \(\frac{2 \pi}{\lambda} =10 \pi\),

2\( \pi f =10 \pi \)

f =5 \(\mathrm{~Hz}\)

⇒ \(\lambda =\frac{1}{5}=0.2 \mathrm{~m}\)

When signs of the coefficient of t and x are opposite it means

⇒ \(\frac{d x}{d t}=v>0\)

i.e. wave is propagating in the direction growing x.

Question 6. A wave travelling in the positive x-direction with amplitude A = 0.2 m, velocity V = 360 ms^-1 and wavelength λ = 60 m, then the correct expression for the wave is:

1. y=0.2 \(\sin \left[2 \pi\left(6 t+\frac{x}{60}\right)\right]\)
2. y=0.2 \(\sin \left[\pi\left(6 t+\frac{x}{60}\right)\right]\)
3. y=0.2 \(\sin \left[2 \pi\left(6 t-\frac{x}{60}\right)\right]\)
4. y=0.2 \(\sin \left[\pi\left(6 t-\frac{x}{60}\right)\right]\)

Answer: 3. y=0.2 \(\sin \left[2 \pi\left(6 t-\frac{x}{60}\right)\right]\)

The general equation of wave travelling in x-direction is given as

y=A \(\sin \left[\frac{2 \pi}{\lambda}(v t-x)\right]\)

Where, A=\(0.2 \mathrm{~m}, v=360 \mathrm{~ms}^{-1}, \lambda=60 \mathrm{~m}\)

The equation becomes, y=\(0.2 \sin \left[\frac{2 \pi}{60}(360 t-x)\right]\)

y=0.2 \(\sin \left[2 \pi\left(6 t-\frac{x}{60}\right)\right]\)

Question 7. If the initial tension on a stretched string is doubled then the ratio of the initial and final speeds of a transverse wave along the string is:

1. 1:1
2. \(\sqrt{2}: 1\)
3. 1: \(\sqrt{2}\)
4. 1: 2

Answer: 3. 1: \(\sqrt{2}\)

We know that the velocity of a transverse wave in a stretched string is, \(\mathrm{v}=\sqrt{\frac{T}{\mu}}\) →  Equation 1

Given = Tension, T = 27

Now, the speed of the wave in the string will be \(v^{\prime}=\sqrt{\frac{2 T}{\mu}}\)  → Equation 2

from eq (1) and (2), we get

∴ \(\frac{v}{v^{\prime}}=\frac{1}{\sqrt{2}}\)

Question 8. A uniform rope of length L and mass \(m_1\) hangs vertically from a rigid support. A block of mass \(m_2\) is attached to the free end of the rope. A transverse pulse wavelength \(\lambda_1\) is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the A rope is \(\lambda_2\). The ratio \(\frac{\lambda_2}{\lambda_1}\) is:

1. \(\sqrt{\frac{m_1+m_2}{m_2}}\)
2. \(\sqrt{\frac{m_2}{m_1}}\)
3. \(\sqrt{\frac{m_1+m_2}{m_1}}\)
4. \(\sqrt{\frac{m_1}{m_2}}\)

Answer: 1. \(\sqrt{\frac{m_1+m_2}{m_2}}\)

Given

A uniform rope of length L and mass \(m_1\) hangs vertically from a rigid support. A block of mass \(m_2\) is attached to the free end of the rope. A transverse pulse wavelength \(\lambda_1\) is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the A rope is \(\lambda_2\).

From the question: Wavelength of transverse pulse,

Also, we know that, \(\lambda=\frac{v}{n}\)  →  Equation 1

Also, we know that,

v= \(\sqrt{\frac{T}{\mu}}\)  →  Equation 2

v= velocity of the wave,

n= frequency of the wave

T= tension in the string

mu= mass per unit length of rope

From eq. (1) and (2), we get,

⇒ \(\lambda =\frac{1}{n} \sqrt{\frac{T}{\mu}}\)

⇒ \(\lambda \propto \sqrt{T}\)

∴ For different cases \(\frac{\lambda_2}{\lambda_1}=\sqrt{\frac{T_2}{T_1}}=\sqrt{\frac{m_1+m_2}{m_2}}\)

Question 9. The equation of a simple harmonic wave is given by:\(y=3 \sin \frac{\pi}{2}(50 t-x)\), where x and y are in metres and t is in seconds. The ratio of maximum particle velocity to the wave velocity is:

1. \(2 \pi\)
2. \(\frac{3}{2} \pi\)
3. 3 \(\pi\)
4. \(\frac{2}{3} \pi\)

Answer: 2. \(\frac{3}{2} \pi\)

We know that and \(v_{\max } =a \omega\)

v =\(n \lambda\)

⇒ \(\frac{v_{\max }}{v} =\frac{a \omega}{n \lambda}\)

= \(\frac{(2 \pi n) a}{n \lambda}=\frac{2 \pi a}{\lambda}\)

= \(\frac{2 \pi a}{\frac{2 \pi}{K}}=\frac{\pi}{2} \times 3=\frac{3 \pi}{2}\)

Question 10. Sound waves travel at 350 m/s through warm air at 3500 m/s through brass. The wavelength of a 700 Hz acoustic wave as it enters brass from warm air:

1. increases by a factor of 20
2. increases by a factor of 10
3. decreases by a factor of 20
4. decreases by a factor of 10

Answer: 2. increases by a factor of 10

Given, Velocity of ware in warm air \(v_1=350 \mathrm{~m} / \mathrm{s}\)

Velocity of ware in brass,\( v_2=3500 \mathrm{~m} / \mathrm{s}\)

We know that,Velocity of sound, v=\(n \lambda\)

⇒ \(\frac{v_1}{v_2}=\frac{n_1 \lambda_1}{n_2 \lambda_2}\)

Since, \(n_1=n_2 \)

=\(\lambda_1 \times \frac{3500}{350}\)

=\(\lambda_1 \times 10\)

⇒ \(\lambda_2=10 \lambda_1 \)

∴ \(\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}\)

Question 11. A transverse wave is represented by y =\(y=A \sin (\omega t-k x)\). For what value of the wavelength is the wave velocity equal to the maximum particle velocity?

1. \(\frac{\pi \mathrm{A}}{2}\)
2. \(\pi A\)
3. 2 \(\pi A\)
4. A

Answer: 3.

Wave velocity v=\(\frac{\omega}{K}=\omega A\)

⇒ \(\frac{\lambda}{2 \pi}\) =A

∴ \(\lambda =2 \pi A\)

Question 12. Two points are located at a distance of 10 m and 15 m from the source of oscillation. The period of oscillation is 0.05 s and the velocity of the wave is 300 m/s. What is the phase difference between the oscillation of two points?

1. \(\frac{\pi}{3}\)
2. \(\frac{2 \pi}{3}\)
3. \(\pi\)
4. \(\frac{\pi}{6}\)

Answer: 2. \(\frac{2 \pi}{3}\)

We know that, Phase-difference, \(\phi=\frac{2 \pi}{\lambda} \times\) path difference

Here path diff., \(\Delta x=15-10=5 \mathrm{~m}\)

Now frequency, v=\(\frac{1}{T}=\frac{1}{0.05}=20 \mathrm{~Hz}\)

velocity \(\mathrm{v}=300 \mathrm{~m} / \mathrm{s}\)

wavelength \(\lambda=\frac{\mathrm{v}}{\mathrm{v}}=\frac{300}{20}=15 \mathrm{~m}\)

Phase difference, \(\Delta \phi=\frac{2 \pi}{\lambda} \times x\)

= \(\frac{2 \pi}{15} \times 5=\frac{2 \pi}{3}\)

Question 13. A transverse wave propagating along the x-axis is represented by \(y(x, t)=8.0 \sin (0.5 \pi x-4 \pi t-\pi / 4)\) where x is in metres and t is in seconds. The speed of the wave is:

1. 8 \(\mathrm{~m} / \mathrm{s}\)
2. 4 \(\pi \mathrm{m} / \mathrm{s}\)
3. 0.5 \(\pi \mathrm{m} / \mathrm{s}\)
4. \(\frac{1}{2} \mathrm{~m} / \mathrm{s}\)

Answer: 1. 8 \(\mathrm{~m} / \mathrm{s}\)

It is given that, \(y(x, t)=8.0 \sin \left(0.5 \pi x-4 \pi t-\frac{\pi}{4}\right)\)

Compare this equation with the standard equation, we have,

y=\(A \sin \left(\frac{2 \pi x}{\lambda}-\frac{2 \pi t}{\mathrm{~T}}+\phi\right)\)

⇒ \(\frac{2 \pi}{\lambda} =0.5 \pi\)

⇒ \(\lambda =\frac{2 \pi}{0.5 \pi}=4 \mathrm{~m}\)

⇒ \(\frac{2 \pi}{T} =4 \pi\)

T =\(\frac{1}{2} \mathrm{~s}\)

∴ \(\mathrm{v}=\frac{\lambda}{T} =\frac{4}{1 / 2}=8 \mathrm{~m} / \mathrm{s}\)

Question 14. A point source emits sound equally in all directions in a non-absorbing medium. Two points P and Q are at distances of 2 m and 3 m respectively from the source. The ratio of the intensities of the wave at P and Q is:

1. 3:2
2. 2:3
3. 9:4
4. 4:9

Answer: 3. 9:4

Given: \(d_1=2 \mathrm{~m}_1, d_2=3 \mathrm{~m}\)

Intensity \(\propto \frac{1}{(\text { distance })^2}\)

⇒ \(I_1 \propto \frac{I}{2^2}\)

And, \(I_2 \propto \frac{1}{3^2}\)

∴ \(\frac{I_1}{I_2}=\frac{9}{4}\)=9: 4

Question 15. The equation of a wave is given by y = a sin\(\left(100 t-\frac{x}{10}\right)\) where x and y are in metres and t in seconds, then the velocity of the wave is:

1. 0.1 m/s
2. 10 m/s
3. 100m/s
4. 1000 m/s

Answer: 4. 1000 m/s

We have, y=A \(\sin \left(100 t-\frac{x}{10}\right)\)

On comparing with the standard wave equation, we get \(\omega=100, k=\frac{1}{10}\)

Velocity of the wave, \(\mathrm{v} =\frac{\omega}{k}=\frac{100}{1 / 10}\)

= \(100 \times 10=1000 \mathrm{~m} / \mathrm{s}\)

Question 16. If Cs be the velocity of sound in air and C be the RMS velocity, then

1. \(I_1+I_2\)
2. \(\left(\sqrt{I_1}+\sqrt{I_2}\right)^2\)
3. \(\left(\sqrt{I_1}-\sqrt{I_2}\right)^2\)
4. \(2\left(I_1+I_2\right)\)

Answer: 3. \(\left(\sqrt{I_1}-\sqrt{I_2}\right)^2\)

We have, velocity, \(C_s=\sqrt{\left(\frac{\gamma p}{\rho}\right)}\) →  Equation 1

where, p is pressure, \(\rho\) is density and \gamma[/latex] is atomicity of gas,

And RMS velocity of gas molecule, C=\(\sqrt{\left(\frac{3 p}{\rho}\right)}\) → Equation 2

From eq. (1) and (2), we get,

⇒ \(\frac{C_s}{C} =\sqrt{\frac{\gamma p}{\rho} \times \frac{\rho}{3 p}}=\sqrt{\frac{\gamma}{3}}\)

∴ \(C_s =C \times \sqrt{\frac{\gamma}{3}}\)

Question 17. Two periodic waves of intensities \(I_1\) and \(I_2\) pass through a region at the same time in the same direction. The sum of the maximum and minimum intensities is:

1. \(I_1+I_2\)
2. \(\left(\sqrt{I_1}+\sqrt{I_2}\right)^2\)
3. \(\left(\sqrt{I_1}-\sqrt{I_2}\right)^2\)
4. \(2\left(I_1+I_2\right)\)

Answer: 4. \(2\left(I_1+I_2\right)\)

I =\(I_1+I_2+2 \sqrt{I_1 I_2} \cos \phi \)

⇒ \(I_{\max } =\left(\sqrt{I_1}+\sqrt{I_2}\right)^2 \)

⇒ \(I_{\min } =\left(\sqrt{I_1}-\sqrt{I_2}\right)^2 \)

⇒ \(I_{\max }+I_{\min } =\left(\sqrt{I_1}+\sqrt{I_2}\right)^2+\left(\sqrt{I_1}-\sqrt{I_2}\right)^2 \)

= \(\left(I_1+I_2+2 \sqrt{I_1 I_2}\right)+\left(I_1+I_2-2 \sqrt{I_1 I}\right)\)

= \(2\left(I_2+I_2\right)\)

Question 18. Two waves of the same frequency and intensity superimpose on each other in opposite phases. After the superposition, the intensity and frequency of waves will:

1. increase
2. decrease
3. remain constant
4. become zero

Answer: 4. become zero

Sound and light are both altered by interference. In sound when the resultant intensity is maximum (in phase), the interference is said to be constructive and when the resultant intensity is minimum or zero, it is said to be destructive (in opposite phase).

Question 19. The length of the string of a musical instrument is 90 cm and has a fundamental frequency of 120 Hz. Where should it be pressed to produce a fundamental frequency of 180 Hz?

1. 75 cm
2. 60 cm
3. 45 cm
4. 80 cm

Answer: 2. 60 cm

Length of string of musical instrument = 90cm = 0.9m

fundamental frequency, \(f_1=120 \mathrm{~Hz}, f_2=180 \mathrm{~Hz}\) .

We know that: \(f \propto \frac{1}{l}\)

⇒ \(\frac{f_1}{f_2}=\frac{l_2}{l_1}\)

⇒ \(l_2=\frac{f_1}{f_2} \times l_1\)

⇒ \(l_2=\frac{120}{180} \times 0.9\)

⇒ \(l_2=\frac{2}{3} \times 0.9=0.6 \mathrm{~m}\)

∴ \(l_2=60 \mathrm{~cm} \text {. }\)

Question 20. A tuning fork with a frequency of 800 Hz produces resonance in a resonance column tube with the upper end open and the lower end closed by the water surface. Successive resonances are observed at lengths 9.75 cm, 31.25 cm and 52.75 cm. The speed of sound in air is:

1. 500 m/s
2. 156 m/s
3. 344 m/s
4. 172 m/s

Answer: 3. 344 m/s

The first and second resonance of the tuning fork of the resonance tube is shown below,

Here,\(l_1=\frac{\lambda}{4} and l_2=\frac{3 \lambda}{4}\)

⇒ \(l_2-l_1 =\frac{3 \lambda}{4}-\frac{\lambda}{4}=\frac{2 \lambda}{4}=\frac{\lambda}{2}\)

⇒ \(\lambda =2\left(l_2-l_1\right)\)

We know that,\( \mathrm{v} =f \lambda\)

⇒ \(\mathrm{v} =800 \times 2(31.25-9.75)\)

= 34400 \(\mathrm{~cm} / \mathrm{s}\)

∴ \(\mathrm{v} =344 \mathrm{~m} / \mathrm{s}\)

Question 21. The fundamental frequency in an open organ pipe is equal to the third harmonic of a closed organ pipe. If the length of the closed organ pipe is 20 cm, the length of the open organ pipe is:

1. 12.5 cm
2. 8 cm
3. 13.3 cm
4. 16 cm

Answer: 3. 13.3 cm

For closed organ pipe.

Third harmonics,\(f=\frac{3 V}{4 l}\)  →  Equation 1

Where f is the length of a closed organ pipe. for open organ pipe, fundamental frequency, \(f=\frac{V}{2 l^{\prime}}\)  →  Equation 2

Where I = length of the open organ pipe.

Equating equation (1) and (2)

⇒ \(\frac{3 \mathrm{~V}}{4 l}=\frac{\mathrm{V}}{2 l^{\prime}}\)

⇒ \(l^{\prime} =\frac{4 l}{3 \times 2}=\frac{2 l}{3}\)

⇒ \(l^{\prime} =\frac{2}{3} \times 20=\frac{40}{3}\)  [Since l = 20 given ]

=13.33 \(\mathrm{~cm}\)

Question 22. A tuning fork is used to produce resonance in a glass tube. The length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27°C, two successive resonances are produced at 20 cm and 73 cm of column length. If the frequency of the tuning fork is 320 Hz, the velocity of sound in air at 27°C is:

1. 350m/s
2. 339 m/s
3. 330m/s
4. 300 m/s

Answer: 2. 339 m/s

Given

A tuning fork is used to produce resonance in a glass tube. The length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27°C, two successive resonances are produced at 20 cm and 73 cm of column length.

For first resonance, \(l_1=\frac{\lambda}{4}\) and second resonance,\(l_2=\frac{3 \lambda}{4}\)

⇒ \(l_2-l_1 =\frac{3 \lambda}{4}-\frac{\lambda}{4}=\frac{\lambda}{2}\)

⇒ \(\lambda =2\left(l_2-l_1\right)\)

Velocity of sound wave

⇒ \(\mathrm{v}=\mathrm{v}\) (Where v= frequency)

⇒ \(\mathrm{v}=\mathrm{v}(2)\left(l_2-l_1\right)\)

⇒ \(\mathrm{v}\)=2[320(0.73-0.202)]

⇒ \(\mathrm{v}=2 \times 320 \times 0.53=339.2 \mathrm{~ms}^{-1}\)

∴ \(\mathrm{v}=339 \mathrm{~ms}^{-1}\)

Question 23. An air column, closed at one end and open at the other, resonates with a tuning fork when the smallest length of the column at 50 cm. The next larger length of the column resonating with the same tuning fork is:

1. 100cm
2. 150 cm
3. 200cm
4. 66.7 cm

Answer: 2. 150 cm

Given

An air column, closed at one end and open at the other, resonates with a tuning fork when the smallest length of the column at 50 cm.

The situation is shown in the given diagram,

⇒ \(L_{\min } =\frac{\lambda}{4}\)

50 =\(\frac{\lambda}{4}\)

⇒ \(\lambda =200 \mathrm{~cm}\)

Next higher length of an column, L =\(\frac{\lambda}{4}+\frac{\lambda}{2}=\frac{3 \lambda}{4}\)

= \(\frac{3}{4} \times 200=150 \mathrm{~cm}\)

Question 24. The second overtone of an open organ pipe has the same frequency as the first overtone of a closed pipe L metre long. The length of the open pipe will be:

1. L
2. 2L
3. 1/2
4. 4L

Answer: 2. 2L

For second overtone (\( 3^{\text {rd }}\) harmonics) in open organ pipe,

⇒ \(\frac{3 \lambda}{2}=l_0\)

⇒ \(\lambda=\frac{2 l_0}{3}\)

for first overtone \(( 3^{\text {rd }}\) harmonics) in closed organ pipe ,

⇒ \(\frac{3 \lambda}{4} =l_c\)

⇒ \(\lambda =\frac{4 l_c}{3}=\frac{4 L}{3}\)

So, \(\frac{2 l_0}{3} =\frac{4 L}{3}\)

∴ \(l_0 =2 L\)

Question 25. The fundamental frequency of a closed organ pipe of length 20 cm is equal to the second overtone of an organ pipe open at both ends. The length of the organ pipe open at both ends is:

1. 80 cm
2. 100 cm
3. 120 cm
4. 140 cm

Answer: 3. 120 cm

For closed organ pipe, frequency of vibration \(f_c\) is given,

⇒ \(f_c=\frac{\mathrm{v}}{4 l}\)

l= length of closed organ pipe and for open organ pipe frequency of vibration is \(f_0\).

⇒ \(f_0=\frac{\mathrm{v}}{2 l}\),

l= length of open organ pipe

According to question, \(f_c =3 f_0\)

⇒ \(\frac{V}{4 l}=\frac{3 V}{2 l^{\prime}}\)

⇒ \(l^{\prime}\) =6 l

∴ \(l^{\prime}=6 \times 20=120 \mathrm{~cm}\)

Question 26. A string is stretched between fixed points separated by 75.0 cm. It is observed to have resonant frequencies of 420 Hz and 315 Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for these strings is:

1. 155 Hz
2. 205 Hz
3. 10.5 Hz
4. 105 Hz

Answer: 4. 105 Hz

Given

A string is stretched between fixed points separated by 75.0 cm. It is observed to have resonant frequencies of 420 Hz and 315 Hz. There are no other resonant frequencies between these two.

Two consecutive resonant frequencies for a string fixed at both ends will be, \(\frac{n \mathrm{v}}{2 l}\) and \(\frac{(n+1)}{2 l} \mathrm{v}\)

⇒ \(\frac{(n+1) \mathrm{v}}{2 l}-\frac{n \mathrm{v}}{2 l}\) =420-315

∴ \(\frac{\mathrm{v}}{2 l} =105 \mathrm{~Hz}\)

Question 27. If \(n_1, n_2 and n_3\) are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency n of the string is given by:

1. \(\frac{1}{n}=\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}\)
2. \(\frac{1}{\sqrt{n}}=\frac{1}{\sqrt{n_1}}+\frac{1}{\sqrt{n_2}}+\frac{1}{\sqrt{n_3}}\)
3. \(\sqrt{n}=\sqrt{n_1}+\sqrt{n_2}+\sqrt{n_3}\)
4. n=\(n_1+n_2+n_3\)

Answer: 1. \(\frac{1}{n}=\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}\)

The string is divided into three points,

⇒ \(l_1\) has frequency \(n_1\)

⇒ \(l_2\) has frequency \(n_2\)

and \(l_3\) has frequency \(n_3\)

Using \(\mathrm{v} =f \lambda\)

⇒ \(\lambda =\frac{\mathrm{v}}{f}\)

⇒ \(l_1 =\frac{\mathrm{v}}{n_1}, l_2=\frac{\mathrm{v}}{n_2}, l_3=\frac{\mathrm{v}}{n_3}\)

⇒ \(l =l_1+l_2+l_3\)

⇒ \(\frac{\mathrm{v}}{n} =\frac{\mathrm{v}}{n_1}+\frac{\mathrm{v}}{n_2}+\frac{\mathrm{v}}{n_3}\)

where, \(\mathrm{v}\) is same in all case,

∴ \(\frac{1}{n}=\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}\)

Question 28. The number of possible natural oscillations of the air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz are (velocity of sound = 340 ms^-1):

1. 4
2. 5
3. 7
4. 6

Answer: 4. 6

For pipe closed at one end, \(f_n=n\left(\frac{v}{4 l}\right)\)

= \(n \times \frac{340}{4 \times 85 \times 10^{-2}}\) =100 n

⇒ \(f_1 =100 \mathrm{~Hz}\)

⇒ \(f_2 =300 \mathrm{~Hz}\)

⇒ \(f_3 =500 \mathrm{~Hz}\)

⇒ \(f_4 =700 \mathrm{~Hz}\)

⇒ \(f_5 =900 \mathrm{~Hz}\)

⇒ \(f_6 =1100 \mathrm{~Hz}\)

∴ This confirms that the number of possible natural oscillations could be 6.

Question 29. If we study the vibration of a pipe open at both ends, then the following statement is not true:

1. Open and will be anti-node.
2. Odd harmonics of the fundamental frequency will be generated.
3. All harmonics of the fundamental frequency will be generated.
4. Pressure change will be maximum at both ends.

Answer: 4. Pressure change will be maximum at both ends.

In the study of the vibration of a pipe open at both ends, the displacement node is the pressure antinode. So, the pressure change will be Maximum at the length \(\frac{1}{2}\) and the pressure variation will be minimum at both ends. The odd and even harmonics will be present in the vibration.

Question 30. The time of reverberation of room A is one second. What will be the time (in seconds) of reverberation of a room, having all the dimensions double those of room A?

1. 1
2. 2
3. 4
4. \(\frac{1}{2}\)

Answer: 2. 2

Reverberation Time, \(T=\frac{0.61 \mathrm{~V}}{\mathrm{~A} S}\)

Where, Z= Volume of room in cubic metres,4= Average absorption coefficient of the room S= Total surface area of the room in square metres

Clearly, T \(\propto \frac{V}{S}\)

⇒ \(\frac{T_1}{T_2} =\left(\frac{V_1}{V_2}\right)\left(\frac{S_2}{S_1}\right)\)

=\(\left(\frac{V}{8 V}\right)\left(\frac{4 S}{S}\right)=\frac{1}{2} \)

∴ \(T_2 =2 T_1=2 \times 1=2 \mathrm{~s}\) . \(( T_1=1 \mathrm{~s}\)

Question 31. Standing waves are produced in a 10 m-long stretched string. If the string vibrates in 5 segments and the wave velocity is 20 m/s, the frequency is:

1. 10 Hz
2. 5 Hz
3. 4 Hz
4. 2 Hz

Answer: 2. 5 Hz

For standing wave, the length of one segment will be \(\frac{\lambda}{2}\)}.

Since there are 5 segments and the total length of the string is 10 \(\mathrm{~m}\).

⇒ \(5 \times \frac{\lambda}{2}\) =10

⇒ \(\lambda =4 \mathrm{~m}\)

∴ Thus, frequency, n=\(\frac{\mathrm{v}}{\lambda}=\frac{20}{4}=5 \mathrm{~Hz}\mathrm{v}=20 \mathrm{~m} / \mathrm{s})\)

Question 32. Which one of the following is a simple harmonic motion?

1. Ball bouncing between two rigid vertical walls.
2. Particles move in a circle with uniform speed.
3. Wave moving through a string fixed at both ends
4. Earth spinning about its own axis

Answer: 3. Wave moving through a string fixed at both ends

In Simple harmonic motion, Individual particles of a medium execute simple harmonic motion about their mean position in a direction perpendicular to the direction of propagation of wave motion. SHM is performed by a wave travelling across a string with both ends fixed

Question 33. In a guitar, two strings A and B made of the same material are slightly out of tune and produce beats of a frequency of 6 Hz. When tension in B is slightly decreased, the beat frequency increases to 7 Hz. if the frequency of A is 530 Hz, the original frequency of B will be:

1. 524 Hz
2. 536 Hz
3. 537 Hz
4. 523 Hz

Answer: 1. 524 Hz

Given

In a guitar, two strings A and B made of the same material are slightly out of tune and produce beats of a frequency of 6 Hz. When tension in B is slightly decreased, the beat frequency increases to 7 Hz.

In the case of beat formation.

Unknown frequency \(v_B=v_A \pm\) beats

Where \(v_A=530 \mathrm{~Hz} \text {, beats }=6 \mathrm{~Hz}\)

⇒ \(v_B=530 \pm 6=536 \text {, or } 524 \mathrm{~Hz}\)

From the question, when tension is. B is slightly decreased, and then the beat frequency increases to 7 Hz. Thus the original frequency B is 524 Hz.

Question 34. Three sound waves of equal amplitudes have frequencies (n – 1), n, (n +1). They superimpose to give beats. The number of beats produced per second will be:

1. 1
2. 4
3. 3
4. 2

Answer: 4. 2

Now divide 1 second into 1,1,2, equal divisions

⇒ \(\frac{1}{1}, \frac{1}{1}, \frac{2}{1}\)

By eliminating common time instants, the total maxima in one second is 2.

Question 35. A source of unknown frequency gives 4 beats/s when sounded with a source of known frequency 250 Hz. The second harmonic of the source of unknown frequency gives five beats per second when sounded with the source of frequency 513 Hz. unknown frequency is:

1. 254 Hz
2. 246 Hz
3. 240 Hz
4. 260 Hz

Answer: 1. 254 Hz

Frequency of unknown source =246 Hz or 254 Hz

second harmonic of this source = 492Hz or 508 Hz

when given 5 beats per second when sounded with a source frequency of 513 Hz.

Therefore, unknown frequency = 254 Hz.

Question 36. Two identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to the occurrence of 6 beat/s when both the wires oscillate together would be:

1. 0.02
2. 0.03
3. 0.04
4. 0.01

Answer: 1. 0.02

According To the Question, the Frequency of the string varies directly as the square root of its tension.

f \(\propto \sqrt{T}\)

⇒ \(\frac{\Delta f}{f} =\frac{1}{2} \cdot \frac{\Delta T}{T}\)

⇒ \(\frac{\Delta T}{T} =2 \cdot \frac{\Delta f}{f}\)

=2 \(\times \frac{6}{600}\)=0.02

Question 37. A tuning fork of frequency 512 Hz makes 4 beats/.? with the vibrating string of beats. The beat frequency decreases to 2 beats when the tension in the piano string is slightly increased. The frequency of the piano string before increasing the tension was:

1. 510 Hz
2. 514 Hz
3. 516 Hz
4. 508 Hz

Answer: 4. 508 Hz

Given

A tuning fork of frequency 512 Hz makes 4 beats/.? with the vibrating string of beats. The beat frequency decreases to 2 beats when the tension in the piano string is slightly increased.

We have, \(n_p \propto \sqrt{\mathrm{T}}\)

⇒ \(n_f\)= frequency of tuning fork =\(\frac{5}{2} \mathrm{~Hz} x\)= Beat frequency =4 beats

Hence, \(n_p-n_f=x \downarrow \text { (wrong) }\)

⇒ \(n_f-n_p=x \downarrow \text { (correct) }\)

∴ \(n_p=n_f-x=512-4=508 \mathrm{~Hz}\)

Question 38. Each of the two strings of length 51.6 cm and 49.1 cm are tensioned separately by 20 N force. The mass per unit length of both the strings is the same and equal to 1 gm1. When both the strings vibrate simultaneously the number of beats is:

1. 5
2. 7
3. 8
4. 3

Answer: 2. 7

Given

Each of the two strings of length 51.6 cm and 49.1 cm are tensioned separately by 20 N force. The mass per unit length of both the strings is the same and equal to 1 gm1.

According to the question, Frequency of first string, \(f_1=\frac{1}{2 l} \sqrt{\frac{T}{m}}\)

=\(\frac{1}{2 \times 51.6 \times 10^{-2}} \sqrt{\frac{20}{10^{-3}}}\)

=137.03 Hz

Frequency of second string,

⇒ \(f_2 =\frac{1}{2 \times 49.1 \times 10^{-2}} \sqrt{\frac{20}{10^{-3}}}\)

=144.01 Hz

Number of beats, \(f_2-f_1\)

= 144-137 = 7 beats

Question 39. Two sound waves with wavelengths 5.0 m and 5.5 m respectively, each propagate in a gas with a velocity of 330 m/s. We expect the following number of beats per second:

1. 6
2. 12
3. 0
4. 1

Answer: 1. 6

⇒ \(\text { Frequency }=\frac{\text { Velocity }}{\text { Wave length }}\)

⇒ \(v_1=\frac{\mathbf{v}}{\lambda_1}=\frac{330}{5}=66 \mathrm{~Hz}\)

and \(v_2=\frac{\mathrm{v}}{\lambda_2}=\frac{330}{5 \cdot 5}=60 \mathrm{~Hz}\)

Number of beats per second =\(v_1-v_2 \)

= 66 – 60 = 6 .

Question 40. Two vibrating tuning forks produce progressive waves given y₁ = 4 sin 500 πt and y₂ = 2 sin 5067πt. Number of beats produced per minute is:

1. 360
2. 180
3. 60
4. 3

Answer: 4. 3

⇒ \(y_1 =4 \sin 500 \pi t \)

⇒ \(y_2 =2 \sin 506 \pi t\)

⇒ \(\omega_1 =500 \pi, \omega_2=506 \pi\)

⇒ \(v_1 =\frac{\omega_1}{2 \pi}=\frac{500 \pi}{2 \pi}\)=250

⇒ \( v_2 =\frac{\omega_2}{2 \pi}=\frac{506 \pi}{2 \pi}\)=253

v = \(v_2-v_1=253-250\)

= 3beats/s

Question 41. Two strings A and B have lengths I_A and I_B and carry masses M_A and M_B at their lower ends, the upper ends being supported by rigid supports, If, n_A and n_B are the frequencies of their vibrations and n_A = 2 n_B, then:

1. I_A = 4I_B, regardless of masses
2. I_B = 4I_B, regardless of masses
3. M_A = 2 M_B, I_A= 2I_B
4. M_B = 2 M_A, IB = 2I_A

Answer: 2. I_B = 4I_B, regardless of masses

We have, the frequency of vibrations of string, n=\(\frac{1}{2 \pi} \sqrt{\frac{g}{I}}\) →   Equation 1

Given, \(n_A=2 n_B\)

⇒ \(\frac{1}{2 \pi} \sqrt{\frac{g}{I_A}}=2 \cdot \frac{1}{2 \pi} \sqrt{\frac{g}{I_B}}\)

⇒ \(\frac{1}{I_A}=\frac{4}{I_B}\)

⇒ \(I_B=4 I_A\)

It is clear from eq (1), that the frequency of vibrations of string does not depend on their masses.

Question 42. A wave has SHM (simple harmonic motion) whose period is 4s while another wave which also possesses SHM has a period of 3s. If both are combined, then the resultant wave will have a period equal to:

1. 4 s
2. 5 s
3. 12 s
4. 3 s

Answer: 3. 12 s

Beats are produced when both waves are combined. Frequency of beats will be \(v_1-v_2=\frac{1}{T_1}-\frac{1}{T_2}=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}\)

Hence, time period = 12 s

Question 43. Two cars moving in opposite directions approach each other with speeds of 22 m/s and 16.5 m/s respectively. The driver of the first car blows a horn having a frequency of 400 Hz. The frequency heard by the driver of the second car is [velocity of sound 340 m/s]:

1. 350 Hz
2. 361 Hz
3. 411 Hz
4. 448 Hz

Answer: 4. 448 Hz

If \(f_0\)= original frequency of source

⇒ \(\mathrm{v}_s\)= speed of source

⇒ \(v_0\)= speed of observer

⇒ \(\mathbf{v}\)= speed of sound

Then if both source and observer are moving towards each other the apparent frequency is \(f_{\mathrm{A}}=f_0\left(\frac{\mathrm{v}+\mathrm{v}_0}{\mathrm{v}-\mathrm{v}_s}\right)\)

In the given question, f₀=400, frequency of horn \({v}_0\)=16.5, speed as observe in 2 case.

⇒ \(\mathrm{v}_s\)= Speed of car =22 m/s

The frequency heard by the driver in the car \(f_{\mathrm{A}} =f_0\left(\frac{\mathrm{v}+\mathrm{v}_0}{\mathrm{v}-\mathrm{v}_s}\right)\)

= 400\(\left(\frac{340+16.5}{340-22}\right)=\frac{356.5 \times 400}{318}\)

= 448 Hz

Question 44. A siren emitting a sound of frequency 800 Hz moves away from an observer towards a cliff at a speed of 15 ms^-1. Then, the frequency of sound that the observer hears in the echo reflected from the cliff is: (Take velocity of ground in air = 330 ms^-1)

1. 800 Hz
2. 838 Hz
3. 885 Hz
4. 765 Hz

Answer: 2. 838 Hz

The frequency of sound observed hear in the echo reflected from the diff. is given by

⇒ \(n^{\prime}=\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_S} n_0\)

⇒ \({\mathrm{v}=330, \mathrm{v}_s=15, n_o=800 \text { given }}\)

⇒ \(n^{\prime}=\frac{330}{330-15} \times 800 \)

= \(\frac{330 \times 800}{315}=838 \mathrm{~Hz}\)v

Question 45. A source of sound S emitting waves of frequency 100 Hz and an observer O are located at some distance from each other. The source is moving with a speed of 19.4 ms^-1 at an angle of 60° with the source observer line as shown in the figure. The observer is at rest. The apparent frequency observed by the observer (velocity of sound in air 330 ms^-1), is:

1. 100 Hz
2. 103 Hz
3. 106 Hz
4. 97 Hz

Answer: 2. 103 Hz

According to question The apparent frequency heard by observer is \(f_0=f_s\left[\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_s \cos 60^{\prime \prime}}\right]\)

Given , \(f_s=100 \mathrm{~Hz}\)

⇒ \(\mathrm{v}=330 \mathrm{~m} / \mathrm{s}\)

⇒ \(\mathrm{v}_s=19.4 \mathrm{~ms}^{-1}\)

⇒ \(f_0=100\left[\frac{330}{330-19.4 \times \frac{1}{2}}\right]\)

= \(100\left[\frac{330}{330-9.7}\right]\)

= \(100\left[\frac{330}{320.3}\right]=103.02 \mathrm{~Hz}\)

Question 46. A speeding motorcyclist sees a traffic jam ahead of him. He shows down to 36 km/h. He finds that traffic has eased and a car moving ahead of him at 18 km/h is honking at a frequency of 1392 Hz. If the speed of sound is 343 m/s, the frequency of the honk as heard by him will be:

1. 1332 Hz
2. 1372 Hz
3. 1412 Hz
4. 1454 Hz

Answer: 3. 1412 Hz

When both observer and source are moving, then the apparent frequency is:

Given: \(\{36 \mathrm{~km} / h=36 \times \frac{5}{18}=10 \mathrm{~ms}^{-1}\).

18 \(\mathrm{~km} / h=18 \times \frac{5}{18}=5 \mathrm{~ms}^{-1}\)

f= \(f_0\left[\frac{\mathrm{v}+\mathrm{v}_0}{\mathrm{v}+\mathrm{v}_{\mathrm{s}}}\right]\left[\text { Since, } f_0=1392 \mathrm{~Hz}\right]\)

= \(1392\left[\frac{343+10}{343+5}\right] \)

= \(1392\left[\frac{353}{348}\right]\)

f= \(1412 \mathrm{~Hz}\)

Question 47. Two sources P and Q produce notes of frequency 660 Hz each. A listener moves from P to Q with a speed of 1 ms^-1. If the speed of sound is 330 m/s, then the number of beats heard by the listener per second will be:

1. 4
2. 8
3. 2
4. zero

Answer: 1. 4

According to the question,

Speed of listener \(\mathrm{v}_L=1 \mathrm{~ms}^{-1}\)

Speed of sound v=330 \mathrm{~ms}^{-1}[/latex]

Frequency of each source v=\(600 \mathrm{~Hz}\)

Apparent frequency due to P=\(\mathrm{v}^{\prime}=\frac{\mathrm{v}\left(\mathrm{v}-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}\)

Apparent frequency due to \(\mathrm{Q}=\mathrm{v}^{\prime \prime}=\frac{\mathrm{v}\left(\mathrm{v}-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}\)

No. of beat heard by the listener per second.

⇒ \(\mathrm{V}^{\prime \prime}-\mathrm{V}^{\prime} =\frac{v\left(\mathrm{v}-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}-\frac{v\left(\mathrm{v}_0-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}\)

= \(\frac{2 v_{\mathrm{L}}}{v}=\frac{2 \times 660 \times 1}{330}\)=4

Question 48. A train moving at a speed of 200 ms¹ toward a stationary object, emits a sound of frequency 100 Hz. Some of the sound reaching the object gets reflected to the train as an echo. The frequency of the echo as detected by the driver of the train is:(speed of sound in air is 300 ms^-1)

1. 3500 Hz
2. 4000 Hz
3. 5000 Hz
4. 3000 Hz

Answer: 3. 5000 Hz

Given

A train moving at a speed of 200 ms¹ toward a stationary object, emits a sound of frequency 100 Hz. Some of the sound reaching the object gets reflected to the train as an echo.

From Doppler’s shift, we have

⇒ \(n^1 =v\left(\frac{v+v_s}{v-v_s}\right)\)

=\(100(\frac{330+220}{330-220})\)

=\(100 \times \frac{550}{110}=5000 \mathrm{~Hz}\)

Question 49. The driver of a car travelling with speed 30 ms^-1 towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330 ms^-1, the frequency of reflected sound as heard by the driver is:

1. 550 Hz
2. 555.5 Hz
3. 720 Hz
4. 500 Hz

Answer: 3. 720 Hz

Applying Doppler’s effect we have,

⇒ \(n^{\prime \prime} =\frac{v+30}{v-30} n \)

= \(\frac{360}{300} \times 600\)

= \(720 \mathrm{~Hz}\)

Question 50. A car is moving towards a high cliff. The driver sounds a horn of frequency f. The reflected sound heard by the driver has a frequency of 2 f. If v is the velocity of sound, then the velocity of the car, in the same velocity units, will be:

1. \(\frac{v}{\sqrt{2}}\)
2. \(\frac{v}{3}\)
3. \(\frac{v}{4}\)
4. \(\frac{v}{2}\)

Answer: 2. \(\frac{v}{3}\)

According to the given conditions,

Cliff is the stationary source of frequency f, where

⇒ \(f^{\prime}=\left(\frac{\mathrm{v}+\mathrm{v}_{\mathrm{car}}}{\mathrm{v}-\mathrm{v}_s}\right) f^{\prime}\)

Frequency heard by the drives or \(f^{\prime \prime}=\left(\frac{\mathrm{v}+\mathrm{v}_{c a r}}{v-v_{\mathrm{s}}}\right) f l\)

2 f=\(\left(\frac{\mathrm{v}+\mathrm{v}_{c a r}}{v-v_{\mathrm{s}}}\right) f\)

⇒ \(v+v_{\text {car }} =2 v-2 v_{\text {car }}\)

⇒ \(3 v_{\text {car }}\) =v

∴ \(v_{\text {car }} =\frac{v}{3}\left(\text { as } v_{\mathrm{s}}=v\right)\)

Question 51. An observer moves towards a stationary source of sound with a speed of 1/5th of the speed of sound. The wavelength and frequency of the source emitted are X and / respectively. The apparent frequency and wavelength recorded by the observer are respectively:

1. 1.2f, 1.2λ
2. 1.2f,  λ
3. f, 1.2 λ
4. 0.8f, 0.8 λ

Answer: 2. 1.2f, λ

Source is stationary,\(\lambda\)= constants

and f=\(\frac{v+v_{\mathrm{S}}}{v} f=\left(1+\frac{v_{\mathrm{S}}}{v}\right) f\)

= \(\left(1+\frac{1}{5}\right)\) f=1.2 f

Question 52. A whistle revolves in a circle with angular speed, co = 20 rad s^-1 using a string of length 50 cm. If the frequency of sound from the whistle is 385 Hz, then what is the minimum frequency heard by an observer who is away from the centre (vrorn6: 340 ms ¹)?

1. 385 Hz
2. 374Hz
3. 394Hz
4. 333 Hz

Answer: 2. 374Hz

Velocity of source is given as \(v_{\text {source }}=0.5 \times 20=10 \mathrm{~ms}^{-1}\)

Minimum frequency is \(f_{\min } =\left(\frac{\mathrm{v}}{\mathrm{v}+\mathrm{v}_s}\right) f\)

= \(\frac{340}{340+10} \times 385=374 \mathrm{~Hz}\)

Question 53. A vehicle, with a horn of frequency h, is moving with a velocity of 30 m/s in a direction perpendicular to the straight line joining the observer and the vehicle. The observer perceives the sound to have a frequency n+ n₁ Then (If the sound velocity in air is 300 m/s):

1. n₁ = 10n
2. n₁ = 0
3. n₁ = 0.1n
4. n₁ = -0.1n

Answer: 2. n₁ = 0

There is no Doppler effect of sound when the velocity of the source (vehicle) is perpendicular to the line between the observer and the source because the component of velocity towards or away from the observer is zero. As a result, there is no apparent difference in frequency. Therefore, n₁ = 0.

Question 54. Two strains move towards each other at the same speed. The speed of sound is 340 m/s. If the height of the tone of the whistle of one of them heard on the other changes 9/8 times, then the speed of each train should be:

1. 20 m/s
2. 2 m/s
3. 200 m/s
4. 2000 m/s

Answer: 1.

Given

Two strains move towards each other at the same speed. The speed of sound is 340 m/s. If the height of the tone of the whistle of one of them heard on the other changes 9/8 times,

According to Doppler’s effect, The apparent frequency of sound heard by the listener differs from the actual frequency of sound generated by the source whenever there is relative motion between the source and the listener.

The apparent frequency of sound wave heard by the listener is \(f=\frac{\mathrm{v}-\mathrm{v}_I}{\mathrm{v}-\mathrm{v}_s} \times f\)

where v is the actual frequency of sound emitted by the source, v. is the source’s velocity, and v1 is the listener’s velocity. If v’= (9/8) v and the source and observer are both moving in the same direction at the same speed (say v), the apparent frequency is

⇒ \(f =f \times\left(\frac{v+v_l}{v+v_s}\right)\)

⇒ \(9 f^{\prime} =f \times \frac{340+\mathrm{v}}{340-\mathrm{v}}\)

17 v =\(340 \times 1\)

or v =\(\frac{340}{17}=20 \mathrm{~m} / \mathrm{s}\)

NEET Physics For Oscillations Multiple Choice Questions

Question 1. The displacement of a particle executing simple harmonic motion is given by, y=\(y=A_0+A \sin \omega t+B \cos \omega t\) Then the amplitude of its oscillation is given by :

1. \(\sqrt{A^2+B^2}\)
2. \(\sqrt{A_0^2+(A+B)^2}\)
3. A+B
4. \(A_0+\sqrt{A^2+B^2}\)

Answer: 1. \(\sqrt{A^2+B^2}\)

Here: y=\(\mathrm{A}_{\mathrm{o}}+A \sin \omega t+B \cos \omega t\)

Equating with SHM ,\( y^{\prime} =y-\mathrm{A}_{\mathrm{o}}=\mathrm{A} \cos \left(\frac{\pi}{2}-\omega t\right)+\mathrm{B} \cos \omega \mathrm{t}\)

=A \(\sin \omega t+B \cos \omega \mathrm{t}\) .

Resultant amplitude, R =\(\sqrt{A^2+B^2+2 A B \cos 90^{\circ}}\)

=\(\sqrt{A^2+B^2}\)

Question 2. The distance covered by a particle undergoing SHM in one time period is (amplitude = A):

1. zero
2. A
3. 2A
4. 4A

Answer: 4. 4A

In an SHM particle moves from the mean position to an extreme position (P) and then returns to the mean position covering the same distance A.

A + A + A + A = 4 A

Question 3. When two displacement represented by \(y_1=a \sin (\omega t)\) and \(y_2=b \cos (\omega t)\) are superimposed, the motion is:

1. not a simple harmonic
2. simple harmonic with amplitude
3. simple harmonic with amplitude \(\sqrt{a^2+b^2}\)
4. simple harmonic with amplitude \(\frac{(a+b)}{2}\)

Answer: 3. simple harmonic with amplitude \(\sqrt{a^2+b^2}\)

From the question, \(y_1 =a \sin \omega t\)

⇒ \(y_2=b \cos \omega t \)

=b \(\sin \left(\omega t+\frac{\pi}{2}\right)\)

Read and Learn More NEET Physics MCQs

Resultant displacement is y=\(y_1+y_2\)=a \(\sin \omega t+b \sin \left(\omega t+\frac{\pi}{2}\right)\)

{Since \(\sin (A+B)\)=\(\sin A \cos B+\cos A \sin B\}\)

y=a \(\sin \omega t+b \sin (\omega t) \cos \frac{\pi}{2}+b \cos (\omega t) \sin \left(\frac{\pi}{2}\right)\)

y= \(a \sin (\omega t)+b \cos (\omega t)\)

Again Let b \(\cos (\omega t)=\mathrm{A} \cos \theta\) →  Equation 1

and a \(\sin (\omega t)=\mathrm{A} \sin \theta\)  → Equation 2

Squaring and Adding eq. (1) and (2)

A = \(\sqrt{a^2+b^2}\)

y = \(\sqrt{a^2+b^2} \sin (\omega t+\theta)\)

∴ \(\sqrt{a^2+b^2}\) is the amplitude of SHM

Question 4. Out of the following functions representing motion of a particle which represents SHM:

1. y=\(\sin \omega t-\cos \omega t\)
2. y=\(\sin ^3 \omega t\)
3. y=\(5 \cos \left(\frac{3 \pi}{4}-3 \omega t\right)\)
4. y=\(1+\omega t+\omega^2 t^2\)

1. Only (4) does not represent SHM
2. (1) and (3)
3. (1) and (2)
4. Only (1)

Answer: 3. (1) and (2)

For a S.H.M. \(\mathrm{a} \alpha \frac{d^2 y}{d t^2} \alpha-y\)

Hence equation y=\(\sin \omega t-\cos \omega t\) and

y= \(5 \cos \left(\frac{3 \pi}{4}-3 \omega t\right)\) are satisfying this condition.

Question 5. Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie in a straight line perpendicular to the paths of the two particles. The phase difference is:

1. zero
2. \(\frac{2 \pi}{3}\)
3. \(\pi\)
4. \(\frac{\pi}{6}\)

Answer: 2. \(\frac{2 \pi}{3}\)

Given

Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie in a straight line perpendicular to the paths of the two particles.

The Equation becomes, \(y_1 =\frac{A}{2}=A \sin \omega t \)

⇒ \(\omega t =30^{\circ}\)

⇒ \(y_2 =\frac{A}{2}=A \sin \left(\omega t+\frac{\pi}{2}\right)\)

= \(\omega t+\frac{\pi}{2}=150^{\circ}\)

phase difference \(\Delta \phi =\phi_2-\phi_1 \)

= \(150-30=120^{\circ}\)

= \(\frac{2 \pi}{3} \mathrm{rad}\)

Question 6. The displacement of a particle along the x-axis is given by x = \(x=\mathrm{a} \sin ^2 \omega t\). The motion of the particle corresponds to:

1. simple harmonic motion of frequency \(\omega / \pi\)
2. simple harmonic motion of frequency\(3 \omega / 2 \pi\)
3. nonsimple harmonic motion
4. simple harmonic motion of frequency \(\pi\omega / 2 \)

Answer: 3. nonsimple harmonic motion

According to the question, x=a \(\sin ^2 \omega t\) →  Equation 1

Differentiating eq. (1) w.r.t. t we get

⇒ \(\frac{d x}{d t}=2 a \omega(\sin \omega t)(\cos \omega t)\)

Again differentiating w.r.t. t we have

a=\(\frac{d^2 x}{d t^2} =2 a \omega^2\left[\cos ^2 \omega t-\sin ^2 \omega t\right]\)

=2 a \(\omega^2 \cos 2 \omega t\)  → Equation 2

The eq. (2) does not satisfy the condition of SHM’ So, motion is not simPle harmonic’

Question 7. A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is

1. \(\frac{T}{8}\)
2. \(\frac{T}{12}\)
3. \(\frac{T}{2}\)
4. \(\frac{T}{4}\)

Answer: 2. \(\frac{T}{12}\)

For equilibrium position, x(t)=a \(\sin \omega t\)

At, x(t)=\(\frac{a}{2}\)

⇒ \(\sin(\frac{\pi}{6})=\sin \omega t {\omega=\frac{2 \pi}{\mathrm{T}}}\)

or \(\frac{\pi}{6}=\frac{2 \pi t}{T}\)

t=\(\frac{T}{12}\)

Question 8. The circular motion of a particle with constant speed is:

1. periodic but not simple harmonic
2. simple harmonic but not periodic
3. period and simple harmonic
4. neither periodic nor simple harmonic

Answer: 1. periodic but not simple harmonic

A particle is a constant-speed circular motion that repeats its motion at regular intervals but does not oscillate around a fixed location. As a result, particle motion is periodic but not simply harmonic’

Question 9. Two simple harmonic motions with the same frequency act on a particle at right angles i.e. along X-axis and 7-axis. If the two amplitudes are equal and the phase difference is \(\frac{\pi}{2}\) the resultant motion will be:

1. a circle.
2. an ellipse with the major axis along the Y-axis.
3. an ellipse with the major axis along the X-axis.
4. a straight line inclined at 45° to the X-axis.

Answer: 1. a circle

The equations of two simple harmonic motions can be written as x=\(a \sin \omega t \) Equation 1

and y=\(a \sin \left(\omega t+\frac{\pi}{2}\right)\)

y=\(a \cos \omega t\) Equation 2

On squaring and adding Eqs. (1) and (2), we get

⇒ \(x^2+y^2 =a^2\left(\sin ^2 \omega t+\cos ^2 \omega t\right)\)

or \(x^2+y^2 =a^2\)

It represents the equation of a circular motion with radius a.

Question 10. A Simple harmonic oscillator has an amplitude of a and a period of T. The time required by it to travel from,\(x=a \text { to } x=\frac{a}{2}\) is:

1. \(\frac{T}{6}\)
2. \(\frac{T}{4}\)
3. \(\frac{T}{3}\)
4. \(\frac{T}{2}\)

Answer: 1. \(\frac{T}{6}\)

We have, the equation of simple harmonic motion given by,

or x =\(a \sin \omega t\)

= \(a \sin \left(\frac{2 \pi}{T}\right) t\)

when, x =a , then

a = \(a \sin \left(\frac{2 \pi}{T}\right) t \)

⇒ \(\sin \left(\frac{2 \pi}{T}\right) t\) =1

⇒ \(\sin \left(\frac{2 \pi}{T}\right) t =\sin \frac{\pi}{2}\)

t =\(\frac{T}{4}\)

when x=\(\frac{a}{2}\), then

⇒ \(\frac{a}{2} =a \sin \left(\frac{2 \pi}{T} \cdot t\right)\)

⇒ \(\sin \left(\frac{2 \pi}{T} t\right) =\sin \frac{\pi}{6}\)

t=\(\frac{T}{12}\)

Hence, the time taken to travel from

x=a to x=\(\frac{a}{2}=\frac{T}{4}-\frac{T}{12}=\frac{T}{6}\)

Question 11. The composition of two simple harmonic motions of equal periods at a right angle to each other and with a phase difference of \(\pi\) results in the displacement of the particles along:

1. circle
2. figure of eight
3. straight line
4. ellipse

Answer: 3. straight line

For simple harmonic motion,

x =\(a \sin \omega \mathrm{t}\)  →  Equation 1

and y =\(b \sin (\omega \mathrm{t}+\pi)\)

y =\(-b \sin \omega \mathrm{t}\)  →  Equation 2

or From eq. (1) and (2), we get

⇒ \(\frac{x}{a} =\sin \omega \mathrm{t} \)

and \(-\frac{y}{b} =\sin \omega \mathrm{t}\)

⇒ \(\frac{x}{a} =-\frac{y}{b}\)

y =\(-\frac{b}{a} x\)

Hence, it is an equation of a straight line

Question 12. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the below figure. y-projection of the radius vector of rotating particle P is :

1. y(t)=\(4 \sin \left(\frac{\pi t}{2}\right)\), where y in m
2. y(t)=\(3 \cos \left(\frac{3 \pi t}{2}\right)\), where y in m
3. y(t)=\(3 \cos \left(\frac{\pi t}{2}\right)\), where y in m
4. y(t)=\(-3 \cos 2 \pi t\), where y in m

Answer: 3. y(t)=\(3 \cos \left(\frac{\pi t}{2}\right)\), where y in m

Here, T=4 s, A=3 m

Time Period, \(\mathrm{T}=\frac{2 \pi}{\omega}\)

⇒ \(\omega =\frac{2 \pi}{T}=\frac{2 \pi}{4}=\frac{\pi}{2} \mathrm{rad} / \mathrm{s}\)

y =a cost \(\omega t=3 \cos \frac{\pi}{2} t\)

Question 13. A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of the velocity is equal to that of its acceleration. Then, its period in seconds is

1. \(\frac{\sqrt{5}}{\pi}\)
2. \(\frac{\sqrt{5}}{2 \pi}\)
3. \(\frac{4 \pi}{\sqrt{5}}\)
4. \(\frac{2 \pi}{3}\)

Answer: 3. \(\frac{4 \pi}{\sqrt{5}}\)

Given the magnitude of the velocity of a particle = magnitude of the acceleration of a particle in SHM  →  Equation 1

The magnitude of the velocity of grice at a displacement from the mean position is, \(\omega \sqrt{A^2-y^2}\), and the magnitude of the acceleration of particles in SHM is \(\omega^2 y\)

Then eq. (1) becomes,

⇒ \(\omega \sqrt{A^2-y^2} =\omega^2 y \)

⇒ \(\omega =\frac{\sqrt{A^2-y^2}}{y}=\frac{\sqrt{(3)^2-(2)^2}}{2}\)

= \(\frac{\sqrt{9-4}}{2}=\frac{\sqrt{5}}{2}\)

Time period, T=\(\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{5} / 2}=\frac{4 \pi}{\sqrt{5}}\)

Time period, T=\(\frac{4 \pi}{\sqrt{5}} s\)

Question 14. Two simple harmonic motions given by, \(x=a \sin \omega \mathrm{t}+\lambda \text { and } y=a \sin \left(\omega t+\delta+\frac{\pi}{2}\right)\)act on a particle simultaneously, then the motion of particle will be

1. circular anti-clockwise
2. circular clockwise
3. elliptical anti-clockwise
4. elliptical clockwise

Answer: 2. circular clockwise

x= a \(\sin (\omega t+\delta)\)

y= \(a \sin \left(\omega t+\delta+\frac{\pi}{2}\right)\)

or y= a \(\cos (\omega t+\delta)\)

Squaring and adding eq. (i) and (ii), we get

⇒ \(x^2+y^2=a^2\left[\sin ^2(\omega t+\delta)+\cos ^2(\omega t+\delta)\right]\)

or \(x^2+y^2=a^2\left(\sin ^2 \theta+\cos ^2 \theta=1\right)\)

This represents a circle.

At \((\omega t+\delta)\)=0 ; x=0, y=a

At \((\omega t+\delta)=\frac{\pi}{2}\) ; x=a, y=0

At \((\omega t+\delta)=\pi\) ; x=0, y=-a

At\( (\omega t+\delta)=\frac{3 \pi}{2}\) ; x=-a, y=0

At \((\omega t+\delta)=2 \pi\) ; x=0, y=a

It is clear That the particle motion is in a circular clockwise direction.

Question 15. The phase difference between displacement and acceleration of a particle in a simple harmonic motion is :

1. \(\frac{3 \pi}{2} \mathrm{rad}\)
2. \(\frac{\pi}{2} \mathrm{rad}\)
3. zero
4. \(\pi \mathrm{rad}\)

Answer: 4. \(\pi \mathrm{rad}\)

In Simple Harmonic Motion, The equation of displacement of the particle is y=\(a \sin \omega t\) → Equation 1

And the equation of acceleration of the particle is, a \(\omega^2 \sin \omega t=a \omega^2 \sin (\omega t+\pi)\)  → Equation 2

From eq. (1) and equation (2)

The phase difference between displacement and acceleration of the particle is :

⇒ \(\phi=(\omega t+\pi)-\omega t\)

⇒ \(\phi=\omega t+\pi-\omega t=\pi \text { radian }=\pi \mathrm{rad}\) .

Question 16. The average velocity of a particle executing SHM complete vibration is :

1. \(A \omega\)
2. \(\frac{A \omega^2}{2}\)
3. zero
4. \(\frac{A \omega}{2}\)

Answer: 3. zero

In one complete vibration, displacement is \(2 \pi \omega\). So, the average velocity in one complete vibration is :

∴ \(\frac{\text { Displacement }}{\text { Time Interval }}=\frac{y_1-y_2}{\mathrm{~T}}\)=0

Question 17. The particle is executing SHM along a straight line. Its velocities at distance x₁ and x₂ from the mean position or v₁ and v₂ respectively. Its period is:

1. \(2 \pi \sqrt{\frac{x_1^2+x_2^2}{v_1^2+v_2^2}}\)
2. \(2 \pi \sqrt{\frac{x_1^2-x_2^2}{v_1^2-v_2^2}}\)
3. \(2 \pi \sqrt{\frac{v_1^2+v_2^2}{x_1^2+x_2^2}}\)
4. \(2 \pi \sqrt{\frac{v_1^2-v_2^2}{x_1^2-x_2^2}}\)

Answer: 2. \(2 \pi \sqrt{\frac{x_1^2-x_2^2}{v_1^2-v_2^2}}\)

We know under SHM if A is the amplitude of  oscillation, then the velocity

⇒ \(v_1^2=\omega^2\left(\mathrm{~A}^2-x_1^2\right)\)

⇒ \(v_2^2=\omega^2\left(\mathrm{~A}^2-x_2^2\right)\)

Where \(x_1\) and \(x_2\) are the displacement of particles from the mean position,

Subtracting eq. (2) from eq (1) we have,

⇒ \(v_2^2-v_1^2 =\omega^2\left(x_2^2-x_1^2\right)\)

⇒ \(\omega =\sqrt{\frac{v_2^2-v_1^2}{x_2^2-x_1^2}}\)

⇒ \(\frac{2 \pi}{T}=\sqrt{\frac{v_2^2-v_1^2}{x_2^2-x_1^2}}\)

T =\(2 \pi \sqrt{\frac{x_2^2-x_1^2}{v_2^2-v_1^2}}\)

Question 18. A particle is executing a simple harmonic motion. Its maximum acceleration is \(\alpha\) and its maximum velocity is \(\beta\). Then, its period of vibration will be:

1. \(\frac{\beta^2}{\alpha^2}\)
2. \(\frac{\alpha}{\beta}\)
3. \(\frac{\beta^2}{\alpha}\)
4. \(\frac{2 \pi \beta}{\alpha}\)

Answer: 4. \(\frac{2 \pi \beta}{\alpha}\)

Acceleration of particles does.ng SHM is,

⇒ \(\alpha=A \omega^2\)  → Equation 1

A= maximum amplitude

⇒ \(\omega\)= angular velocity of particle

Again Maximum velocity,

⇒ \(\beta=A \omega\)  → Equation 2

From eq. (1) and (2) we have

⇒ \(\frac{\alpha}{\beta}=\frac{A \omega^2}{A \omega}=\omega=\frac{2 \pi}{T}\)

T=\(\frac{2 \pi \beta}{\alpha}\)

Time period of vibration, T=\(\frac{2 \pi \beta}{\alpha}\)

Question 19. The oscillation of a body on a smooth horizontal surface is represented by the equation, x = \(x=A \cos (\omega t)\)

1. where, x = displacement at time t
2. \(\omega\) = frequency of oscillation
3. Which one of the following graphs shows correctly the variation a with t?
4. Here, a = acceleration at time t,T= time period

Answer: 1. where, x = displacement at time t

The oscillation of the body on a smooth horizontal surface u.

X= \(A \cos \omega t\)

Where, X= displacement at t

⇒ \(\omega\)= frequency of oscillation

A=Amplitude

Here at t=0, X=A

at t=\(\frac{T}{4}, X=A \cos \left(\frac{2 \pi}{T} \times \frac{T}{4}\right)=A \cos \frac{\pi}{2}\)=0

at \(t=\frac{T}{2}, X=A \cos \left(\frac{2 \pi}{T} \times \frac{T}{2}\right)=\mathrm{A} \cos \pi=-\mathrm{A}\)

Question 20. A particle of mass m oscillates along the x-axis according to equation x = a sin \(\omega\). The nature of the graph between the momentum and displacement of the particle is:

1. Circle
2. Hyperbola
3. Ellipse
4. A straight line passing through the origin

Answer: 3. Ellipse

According to the question, x =\(\mathrm{a} \sin \omega t\)

⇒ \(\frac{x}{a} =\sin \omega t\)  → Equation 1

Now velocity v=\(\frac{d x}{d t}=a \omega \cos \omega t\)

⇒ \(\frac{v}{a \omega}=\cos \omega t\)  →  Equation 2

From eq. (1) and (2)

⇒ \(\frac{x^2}{a^2}+\frac{v^2}{a^2 \omega^2}=\sin ^2 \omega t+\cos ^2 \omega t\)

⇒ \(\frac{x^2}{a^2}+\frac{v^2}{a^2 \omega^2}\)=1

∴ This is the equation of an ellipse. So the graph between the moment and displacement of the particle is ellipse.

Question 21. A simple pendulum performs simple harmonic motion x = 0 with an amplitude a and period T. The speed of the pendulum at x =\(\frac{a}{2}\) will be:

1. \(\frac{\pi a \sqrt{3}}{2 T}\)
2. \(\frac{\pi a}{T}\)
3. \(\frac{3 \pi^2 a}{T}\)
4. \(\frac{\pi a \sqrt{3}}{T}\)

Answer: 4. \(\frac{\pi a \sqrt{3}}{T}\)

We know that, V =\(\frac{d y}{d t}=A \omega \cos \omega t\)

= \(A \omega \sqrt{1-\sin ^2 \omega t}\)

= \(A \omega \sqrt{A^2-y^2}\)

Here, y =\(\frac{a}{2}\)

V = \(\omega \sqrt{a^2-\frac{a^2}{4}}=\omega \sqrt{\frac{3 a^2}{4}}\)

= \(\frac{2 \pi}{T} \frac{a \sqrt{3}}{2}=\frac{\pi a \sqrt{3}}{T}\)

Question 22. Which of the following equations of motion represents simple harmonic motion?

1. Acceleration = \(-k_0 x+k_1 x^2\)
2. Acceleration = – k(x + a)
3. Acceleration = k(x + a)
4. Acceleration = kx

Answer: 2. Acceleration = – k(x + a)

Here acceleration a(\(\alpha\)-displacement)

A \(\propto-y\)

A = \(-\omega^2 y \)

A = \(-\frac{k}{m} y\)

A =-k y

And y =x+a

acceleration =-k(x+a)

Question 23. Two simple harmonic motions of angular frequency 100 and 1000 rad \(\mathrm{s}^{-1}\) have the same displacement amplitude. The ratio of their maximum acceleration is:

1. 1: 10
2. 1: 10²
3. 1: 10³
4. 1: 10⁴

Answer: 2. 1: 10²

Acceleration of SHM is, \(a_{\max } =-\omega^2 A\)

or \(\frac{\left(a_{\max }\right)_1}{\left(a_{\max }\right)_2} =\frac{\omega_1^2}{\omega_2^2}\)(A remains same )

or \(\frac{\left(a_{\max }\right)_1}{\left(a_{\max }\right)_2} =\frac{(100)^2}{(1000)^2}=\left(\frac{1}{10}\right)^2 \)

= \(1: 10^2\)

Question 24. A point performs simple harmonic oscillation of period T and the equation of motion is given by x = \(x=a \sin (\omega t+\pi / 6)\). After the elapse of what fraction of the period the velocity of the point will be equal to half of its maximum velocity?

1. \(\frac{T}{8}\)
2. \(\frac{T}{6}\)
3. \(frac{T}{3}\)
4. \(\frac{T}{12}\)

Answer: 4. \(\frac{T}{12}\)

The equation is, x=\(a \sin \left(\omega t+\frac{\pi}{6}\right)\)  → Equation 1

Differentiating we get, v=\(\frac{d x}{d t}=a \omega \cos \left(\omega t+\frac{\pi}{6}\right)\) (Now v=\(\frac{a \omega}{2})\)

⇒ \(\frac{a \omega}{2}=a \omega \cos \left(\omega t+\frac{\pi}{6}\right)\)

⇒ \(\frac{1}{2}=\cos \left(\omega t+\frac{\pi}{6}\right)\)

⇒ \(\cos \frac{\pi}{3} =\cos \left(\omega t+\frac{\pi}{6}\right)\)

⇒ \(\omega t+\frac{\pi}{6} =\frac{\pi}{3}\)

or \(\omega t =\frac{\pi}{6}\)

t =\(\frac{\pi}{6 \omega}=\frac{\pi \times T}{6 \times 2 \pi}=\frac{T}{12}\)

Thus at\( \frac{T}{12}\) velocity of the point will be equal to half of its maximum velocity.

Question 25. The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is :

1. \(\pi\)
2. \(0.70 \pi\)
3. zero
4. \(0.5 \pi\)

Answer: 4. \(0.5 \pi\)

Let y=\(A \sin \omega t=A \omega^2 \sin (\omega t+\pi)\)

⇒ \(\frac{d y}{d t} =A \omega \cos \omega t\)

= \(A \omega \sin \left(\omega t+\frac{\pi}{2}\right)\)

Acceleration,\(\frac{d^2 y}{d x^2}=-A \omega^2 \cos \omega t=A \omega^2 \sin (\omega t+\pi)\)

Phase difference =\(\pi-\frac{\pi}{2}\)

Question 26. A particle executing simple harmonic motion of amplitude 5 cm has a maximum speed of 31.4 cm/s. The frequency of its oscillation is:

1. 4 Hz
2. 3 Hz
3. 2 Hz
4. 1 Hz

Answer: 4. 1 Hz

Here a=5 \(\mathrm{~cm}, V_{\max }=\frac{31.4 \mathrm{~cm}}{\mathrm{~s}}\)

⇒ \(V_{\max }=\omega a=31.4=2 \pi \mathrm{v} \times 5\)

31.4=10 \(\times 3.14 \times v \)

v=1 \(\mathrm{~Hz}\)

Question 27. Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion?

1. When v is maximum, a is maximum
2. The value of a is zero, whatever may be the value of v
3. When v is zero, a is zero
4. When v is maximum a is zero

Answer: 4. When v is maximum a is zero

In SHM, Velocity = \(A \omega \sin \left(\omega t+\frac{\pi}{2}\right)\)

Acceleration=A \(\omega^2 \sin (\omega t+\pi)\)

This shows that v is max then a is zero.

Question 28. A particle starts a simple harmonic motion from the mean position. Its amplitude is a and its period is T. What is its displacement when its speed is half of its maximum speed?

1. \(\frac{\sqrt{2}}{3} a\)
2. \(\frac{\sqrt{3}}{2} a\)
3. \(\frac{2}{\sqrt{3}} a\)
4. \(\frac{a}{\sqrt{2}} a\)

Answer: 2. \(\frac{\sqrt{3}}{2} a\)

At any given time, the velocity of the particle executing SHM is defined as the rate of change of its displacement.

Let the displacement of the particle at an instant be given by

Velocity, v = \(\frac{d x}{d t}=\frac{d(a \sin \omega t)}{d t}\)

=\(a \omega t \cos \omega t\)

= \(a \omega \sqrt{\left(1-\sin ^2 \omega t\right)}\)

= \(a \omega \sqrt{\left(1-\frac{x^2}{a^2}\right)}=w \sqrt{\left(a^2-x^2\right)}\)

At mean position, x=0

⇒ \(v_{\max }=\omega a\)

According to question, v=\(\frac{\mathrm{v}_{\max }}{2}=\frac{\mathrm{a} \omega}{2}\)

But, v=\(\omega \sqrt{a^2-x^2}\)

= \(\frac{a \omega}{2}=\omega \sqrt{a^2-x^2}\)

Or x=\(\frac{\sqrt{3}}{2} a\)

Question 29. A body executes SHM with an amplitude a. At what displacement from the mean position, the potential energy of the body is one-fourth of its total energy?

1. \(\frac{\mathrm{a}}{4}\)
2. \(\frac{a}{2}\)
3. \(\frac{3 a}{4}\)
4. Some other fraction of a

Answer: 2. \(\frac{a}{2}\)

We have, the potential energy of a body executing SHM, U=\(\frac{1}{2} m \omega^2 x^2\)

The total energy of the body executing SHM,

E=\(\frac{1}{2} m \omega^2 a^2\)

According to the question, U =\(\frac{1}{4} E \)

⇒ \(\frac{1}{2} m \omega^2 x^2 =\frac{1}{4} \times \frac{1}{2} m \omega^2 a^2 \)

⇒ \(x^2 =\frac{a^2}{4}\)

x =\(\frac{a}{2}\)

Question 30. A particle moving along the X-axis executes simple harmonic motion, and then the force acting on it is given by where A and K are positive constants.

1. – AKx
2. Acos Kx
3. Aexp(-Ax)
4. AKx

Answer: 1. – AKx

If a particle in simple harmonic motion moves x distant from its equilibrium position, the magnitude of the restoring force 17acting on the particle at that instant is given by F =-kx

where k is known as the force constant. Hence, in given options, option (A) is correct. Here, k = Ak.

Question 31. A body is executing simple harmonic motion with frequency V, the frequency of its potential energy is:

1. n
2. 2n
3. 3n
4. 4n

Answer: 1. n

Given, SHM frequency = n

PE frequency =?

Since PE frequency is the same as SHM frequency.

Question 32. A particle of mass m is released from rest and follows a parabolic path as shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time:

Answer: 4.

Motion starts from an extreme position and for small displacement it is SHM.

∴ \(y=\mathrm{A} \cos (\omega t+\phi)\)

Question 33. The particle executing simple harmonic motion has a kinetic energy \(K_0 \cos ^2 \omega t\)t. The maximum values of the potential energy and the total energy are respectively:

1. \(K_0 / 2\) and \( K_0\)
2. \(K_0 \)and \( 2 K_0\)
3. \(K_0 \)and \( K_0\)
4. \(0\) and \( 2 K_0\)

Answer: 3. \(K_0\) and \( K_0\)

⇒ \(K. E. =K_0 \cos ^2 \omega t\)

Maximum P. E. Maximum K. E. Total energy

= \(K_0\)

Question 34. A particle of mass m oscillates with simple harmonic motion between points X₁ and X₂, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph:

Answer: 1.

PE in SHM =\(\frac{1}{2} K x^2\) →  equation of parabola

Question 35. The potential energy of a simple harmonic oscillator when the particle is halfway to its endpoint is:

1. \(\frac{2}{3} E\)
2. \(\frac{1}{8} E\)
3. \(\frac{1}{4} E\)
4. \(\frac{1}{2} E\)

Answer: 3. \(\frac{1}{4} E\)

P.E. =\(\frac{1}{2} K x^2 \)

=\(\frac{1}{2} K\left(\frac{x}{2}\right)^2=\frac{E}{4}\)

Question 36. The displacement between the maximum potential energy (P.E.) position and the maximum energy (K.E.) position for a particle executing simple harmonic motion is:

1. \(\pm \frac{a}{2}\)
2. \(\pm \mathrm{a}\)
3. \(\pm 2 \mathrm{a}\)
4. \(\pm 1\)

Answer: 2. \(\pm \mathrm{a}\)

The K.E. of pendulum, K.E.=\(\frac{1}{2} K\left(a^2-y^2\right)\)

and P.E. of pendulum =\(\frac{1}{2} K Y^2\)

when y = 0 (mean position) K.E. is maximum and PE is 0

When: 0, K.E. is 0 and P.E. is maximum.

The displacement between the position of maximum potential energy and maximum kinetic energy is \(\pm\) a

Question 37. In SHM restoring force is F = – kx, where k is force constant, x is displacement and a is amplitude of motion, then total energy depends upon:

1. k, a and m
2. k, x, m
3. k, a
4. k, x

Answer: 3. k, a

In simple harmonic motion, the total energy = Potential energy + Kinetic energy

or E = U + K

= \(\frac{1}{2} m \omega^2 x^2+\frac{1}{2} m \omega^2\left(a^2-x^2\right)\)

= \(\frac{1}{2} m \omega^2 a^2+\frac{1}{2} k a^2 \)

Where, k = force constant = \(m \omega^2\)

Question 38. In a simple harmonic motion, when the displacement is one-half the amplitude, what fraction of the total energy is kinetic?

1. Zero
2. \(\frac{1}{4}\)
3. \(\frac{1}{2}\)
4. \(\frac{3}{4}\)

Answer: 4. \(\frac{3}{4}\)

The total energy of a particle executing SHM at instant time t,

E=\(\frac{1}{2} m^2 \omega a^2\)  → Equation 1

and kinetic energy of the particle at instant t,

⇒ \(E_K=\frac{1}{2} m \omega^2\left(a^2-x^2\right)\)  → Equation 2

when x =\(\frac{a}{2}\),

⇒  \(E_K =\frac{1}{2} m \omega^2\left(a^2-\frac{a^2}{4}\right)\)

=\(\frac{1}{2} m \omega^2 \times \frac{3}{4} a^2 \)

⇒ \(E_K =\frac{1}{2} \times \frac{3}{4} m \omega^2 a^2\) →  Equation 3

Or From Eqs. (1) and (3), we get

⇒  \(\frac{E_K}{E} =\frac{3}{4}\)

∴ \(E_K \frac{3}{4} E\)

Question 39. The angular velocity and the amplitude of a simple pendulum are co and a respectively. At a displacement x from the mean position, if its kinetic energy is T and potential energy is U, then the ratio of T to U is

1. \(\left(\frac{a^2-x^2 \omega^2}{x^2 \omega^2}\right)\)
2. \(\frac{x^2 \omega^2}{\left(a^2-x^2 \omega^2\right)}\)
3. \(\frac{\left(a^2-x^2\right)}{x^2}\)
4. \(\frac{x^2}{\left(a^2-x^2\right)}\)

Answer: 3. \(\frac{\left(a^2-x^2\right)}{x^2}\)

Given

The angular velocity and the amplitude of a simple pendulum are co and a respectively. At a displacement x from the mean position, if its kinetic energy is T and potential energy is U

Let us consider a particle of mass m that performs linear SHM with an amplitude of, a and a constant angular frequency. Let us assume that the particle’s displacement is x, which is determined by r seconds after starting from the mean position.

We have, x=\(a \sin \omega t\)

So, the potential energy of the particle is, \(\mathrm{U}=\frac{1}{2} m \omega^2 x^2\) → Equation 1

and kinetic energy of particle is, T=\(\frac{1}{2} m \omega^2\left(a^2-x^2\right)\) →  Equation 2

From Eqs. (1) and (2), we get,

⇒  \(\frac{T}{U}=\frac{a^2-x^2}{x^2}\)

Question 40. A particle, with restoring force proportional to displace¬ment and resisting force proportional to velocity is subjected to a force F \(\sin \omega t\). If the amplitude of the particle is maximum for \(\omega=\omega_1\), and the energy of the particle is maximum for \(\omega=\omega_2\), then

1. \(\omega_1=\omega_0 and \omega_2 \neq \omega_0\)
2. \(\omega_1=\omega_0 and \omega_2=\omega_0\)
3. \(\omega_1 \neq \omega_0 and \omega_2=\omega_0 \)
4. \(\omega_1 \neq \omega_0 and \omega_2 \neq \omega_0\)

Answer: 3. \(\omega_1 \neq \omega_0 and \omega_2=\omega_0 \)

As we know the energy of the particle is maximum at natural frequency. Since the restoring force is proportional to the displacement and the resisting force is proportional to velocity.

So, \(\omega_1 \neq \omega_0 \)

And, \(\omega_2 =\omega_0\)

Question 41. Two pendulums of length 121 cm and 100 cm start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is:

1. 11
2. 9
3. 10
4. 8

Answer: 1. 11

Let us consider,L=121 \(\mathrm{~cm}=1.21 \mathrm{~m} ; L^1=100 \mathrm{~cm}=1 \mathrm{~m}\)

T= longer pendulum; \(\mathrm{T}^1\)= shorter pendulum we know,

T=\(2 \pi \sqrt{\frac{l}{g}} \Rightarrow \mathrm{T} \propto \sqrt{l}\)

⇒  \(\frac{T}{T^1} \propto \sqrt{\frac{L}{L^1}}\)

⇒  \(\frac{T}{T^1} \propto \sqrt{\frac{1.21}{1}}=\frac{1.1}{1}\)

10 \(\mathrm{~T}=11 \mathrm{~T}^1\)

So, 10 vibrations of the longer pendulum: 1L vibration of a shorter pendulum

Question 42. A spring is stretched by 5 cm by a force of 10N. The period of the oscillations when a mass of 2 kg is suspended by it is:

1. 0.0628 s
2. 6.28 s
3. 3.14 s
4. 0.628 s

Answer: 4. 0.628 s

Given, Stretch(x)=5cm

Force (F) = 10 N

Mass (m) = 2ke

Time period, T =?

We know, that, the force constant of spring, \(\mathrm{K}=\frac{F}{x}\)

⇒  \(\mathrm{K} =\frac{10}{0.05}=200 \mathrm{~N} / \mathrm{m}\)

⇒  \(\omega =\frac{2 \pi}{\mathrm{T}}\)

⇒  \(\frac{4 \pi^2}{\mathrm{~T}^2} =\frac{k}{m}\)

⇒  \(\mathrm{~T}^2 =4 \pi^2 \frac{m}{k}\)

= \(-2 \pi \sqrt{\frac{m}{\mathrm{~K}}}\)

⇒  \(\mathrm{T}^2 =4 \pi^2 \frac{m}{k}\)

= \(-2 \pi \sqrt{\frac{m}{\mathrm{~K}}}\)

⇒  \(\mathrm{~T} =2 \pi \sqrt{\frac{2}{200}}\)

=\(2 \pi \sqrt{\frac{1}{100}}\)

=\(\frac{2 \pi}{10}\)

∴ \(\mathrm{~T} =\frac{6.28}{10}=0.628 \mathrm{~s}\)

Question 43. A pendulum is hung from the roof of a sufficiently high building and is moving freely from end to end like a simple harmonic oscillator. The acceleration of the bob of the pendulum is 20 m/s² at a distance of 5 m from the mean position. The period of oscillation is:

1. 2s
2. \(\pi s\)
3. 2 \(\pi s\)
4. 1 \(\mathrm{~s}\)

Answer: 2. \(\pi s\)

Given

A pendulum is hung from the roof of a sufficiently high building and is moving freely from end to end like a simple harmonic oscillator. The acceleration of the bob of the pendulum is 20 m/s² at a distance of 5 m from the mean position.

Acceleration of particle executing SHM at position is given as

⇒  \(|a| =\omega^2 y \) →  Equation 1

Here a = \(20 \mathrm{~ms}^{-1}\)

yy =\(5 \mathrm{~m}\)

20 =\(\omega^2(5)\)

⇒  \(\omega^2\) =4

⇒ \(\omega =2 \mathrm{rad} / \mathrm{s}\)

Time period, T =\(\frac{2 \pi}{\omega}=\frac{2 \pi}{2}=\pi \mathrm{s}\)

T =\(\pi s\)

Question 44. A spring of force constant k is cut into lengths of ratio 1: 2 : 3. They are connected in series and the new force constant is k. If they are connected in parallel and the force constant is k”, then K’: k” is:

1. 1: 6
2. 1: 9
3. 1: 11
4. 1: 14

Answer: 3. 1: 11

Given

A spring of force constant k is cut into lengths of ratio 1: 2 : 3. They are connected in series and the new force constant is k. If they are connected in parallel and the force constant is k”

Spring constant \(\propto \frac{1}{\text { length }}\)

K=\(\frac{1}{l}\)

i.e. \(K_1=6 K, K_2=3 K and K_3\)=2 K

In series, \(\frac{1}{K^{\prime}}=\frac{1}{6 K}+\frac{1}{3 K}+\frac{1}{2 K}\)

⇒  \(\frac{1}{K^{\prime}}=\frac{6}{6 K}\)

⇒  \(K^{\prime}\)=K

⇒  \(K^{\prime \prime}=6 K+3 K+2 K=11 K\)

⇒ \(\frac{K^{\prime}}{K^{\prime \prime}}=\frac{1}{11}\)

∴ \(K^{\prime}: K^{\prime \prime}\)=1: 11

Question 45. A body of mass m is attached to the lower end of a spring whose end is fixed. The spring has negligible mass When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1 kg. The time period of oscillations becomes 5 s. The value of m in kg is:

1. \(\frac{3}{4}\)
2. \(\frac{4}{3}\)
3. \(\frac{16}{9}\)
4. \(\frac{9}{16}\)

Answer: 4. \(\frac{9}{16}\)

Given

A body of mass m is attached to the lower end of a spring whose end is fixed. The spring has negligible mass When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1 kg. The time period of oscillations becomes 5 s.

According to the question, the diagram is

Time period, T=\(2 \pi \sqrt{\frac{m}{k}}\)

⇒  \(\mathrm{I}^{\text {st }} \text { case, }=T_1=2 \pi \sqrt{\frac{m}{k}}\)  → Equation 1

⇒  \(II ^{\text {nd }}\) case when mass m is increased by 1 \(\mathrm{~kg}\) then mass becomes (m+1)

⇒  \(T_2=2 \pi \sqrt{\frac{m+1}{m}}\) →  Equation 2

from eq. (1) and (2) \(\omega_0\) get

⇒  \(\frac{T_2}{T_1}=\sqrt{\frac{m+1}{m}}\)

⇒  \(\frac{5}{3}=\sqrt{\frac{m+1}{m}}\)

⇒  \(\frac{m+1}{m}=\frac{25}{9} \)

⇒  \(1+\frac{1}{m}=\frac{25}{9}\)

∴ \( m=\frac{9}{16} \mathrm{~kg}\)

Question 46. The period of oscillation of a mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be:

1. T
2. \(\frac{T}{\sqrt{2}}\)
3. 2T
4. \(\sqrt{2} T\)

Answer: 4. \(\sqrt{2} T\)

Time period of simple pendulum T

-T = \(2 \pi \sqrt{\frac{\mathrm{M}}{k}}\)

When mass is double then \(T^{\prime} =2 \pi \sqrt{\frac{2 M}{k}}=\sqrt{2}\left(2 \pi \sqrt{\frac{M}{k}}\right)\)

= \(\sqrt{2} T\)

Question 47. A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion so that the mass gets detached from the pan (take g = 10 m/s²)?

1. 10.0 cm
2. any value less than 12.0 cm
3. 4.0 cm
4. 8.0 cm

Answer: 1. 10.0 cm

Given

A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m.

For Given Condition, \(m g =m \omega^2 a=k a\)

a =\(\frac{m g}{k}=\frac{2 \times 10}{200}\)

=0.1=10 \(\mathrm{~cm}\)

Question 48. The time period of mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be:

1. \(\frac{T}{4}\)
2. T
3. \(\frac{T}{2}\)
4. 2T

Answer: 3. \(\frac{T}{2}\)

Let K = force constant of spring and

K = force constant of each part then

⇒  \(\frac{1}{K} =\frac{4}{K^{\prime}}\)

⇒  \(K^{\prime}\) =4 K

Time period =\(2 \pi \sqrt{\frac{m}{4 K}}\)

= \(\frac{1}{2} \times 2 \pi \sqrt{\frac{m}{4 K}}=\frac{T}{2}\)

Question 49. The time period of a simple pendulum is 2 s. If its length is increased by 4 times, then its period becomes:

1. 16 s
2. 12 s
3. 8 s
4. 4 s

Answer: 4. 4 s

We have, time period of a simple pendulum

T=2 \(\pi \sqrt{\frac{l}{g}}\)

where, l= length of the pendulum

g= acceleration due to gravity

T \(\propto \sqrt{l}\)

Hence, \(\frac{T_2}{T_1}=\sqrt{\frac{l_2}{l_1}}\)  → Equation 1

Given, \(l_2=4 l_1, T_1=2 \mathrm{~s}\)

Substituting these values in Eq. (i), we get

⇒  \(T_2=\sqrt{\frac{4 l_1}{l_1}} \times 2=2 \times 2=4 \mathrm{~s}\)

Question 50. The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are:

1. kg ms^-1
2. kg ms^-2
3. kg s^-1
4. kg s

Answer: 3. kg s^-1

It is given that force \(\propto\) velocity

⇒ \(F \propto V \)

F =K V

K = \(\frac{F}{V}\)

Unit of K =\(\frac{F}{V}=\mathrm{kg} \mathrm{s}^{-1}\)

Question 51. When an oscillator completes 100 oscillations its amplitude reduces to \(\frac{1}{3}\) of the initial value. What will be its amplitude when it completes 200 oscillations?

1. \(\frac{1}{8}\)
2. \(\frac{2}{3}\)
3. \(\frac{1}{6}\)
4. \(\frac{1}{9}\)

Answer: 1. \(\frac{1}{8}\)

Let \(a_0\) be the initial amplitude and b be the damping constant

The used formula is a=\(a_0 e^{-b t}\)

In Ist case : t=100 T and a=\(\frac{a_0}{3}\)

⇒ \(\frac{a_0}{3} =a_0 e^{-b(100 T)}\)

⇒ \(e^{-b \times 100 T} =\frac{1}{3}\)

In 2nd case : t =200 T

a = \( a_0 e^{-200 b T}\)

a = \(a_0\left(e^{-100 b T}\right)^2\)

a = \(a_0\left(\frac{1}{3}\right)^2\)

a = \(\frac{a_0}{9}\)

Question 52. In case of a forced vibration, the resonance peak becomes very sharp when the:

1. damping force is small
2. restoring force is small
3. applied periodic force is small
4. the quality factor is small

Answer: 1. The damping force is small

Less damping gives a taller and narrower resonance peak.

NEET Physics For Kinetic Theory Multiple Choice Questions

Question 1. The volume occupied by the molecules contained 4.5 kg water at STP, if the intermolecular forces vanish away is:

1. 5.6 x 10⁶ m³
2. 5.6 x 10³ m³
3. 5.6 x 10^-3m³
4. 5.6 m³

Answer: 4. 5.6 m³

At STP, \(\mathrm{T}=273 \mathrm{~K}, \mathrm{P}=10^5 \mathrm{~N} / \mathrm{m}^2\)

Number of moles of water,\(\mathrm{n} =\frac{\text { mass of water }}{\text { molecular weight of water }}\)

= \(\frac{4.5}{1.8 \times 10^{-2}}\)=250

Using equation, \(\mathrm{PV}=\mathrm{nRT}\)

= \(\frac{\mathrm{nRT}}{\mathrm{P}}=\frac{250 \times 8.3 \times 273}{10^5}\)

= \(5.6 \mathrm{~m}^3\)

Question 2. A given sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule of the gas is m. Which of the following gives the density of the gas?

1. \(\frac{P}{(k T)}\)
2. \(\frac{P m}{(k T)}\)
3. \(\frac{P}{(k T V)}\)
4. mkT

Answer: 2. \(\frac{P m}{(k T)}\)

If, m = mass of gas

v = Volume of gas

⇒ \(\rho=\frac{m}{V}\)= Density of gas

Pressure P =\(\frac{1}{2} \rho V_{\text {rms }}^2\)

= \(\frac{1}{3} \rho \frac{3 R T}{M_0}=\frac{\rho R T}{M_0}\)

⇒ \(\left\{\text { Where, } V_{\text {rms }}=\sqrt{\frac{3 R T}{K N_A T}}\right\}\)

⇒ \(\rho =\frac{P M_0}{R T}=\frac{P M N A}{K N_A T}\)

∴ \(\rho =\frac{P m}{K T}\)

Read and Learn More NEET Physics MCQs

Question 3. In the given (V-T) diagram, what is the relation between pressure p₁ and p₂.

1. P2 = P₁
2. P₂>P₁
3. P₂<P₁
4. Cannot be predicted

Answer: 3. P2<P1

As we know,

PV = nRT

⇒ \(\frac{\mathrm{V}}{\mathrm{T}}=\frac{\mathrm{nR}}{\mathrm{P}}\)

The slope of the graph \(\propto \frac{1}{P}\).

Question 4. At 10°C the value of the density of a fixed mass of an ideal gas divided by its pressure is x. At 110°C this ratio is:

1. x
2. \(\frac{383}{283} x\)
3. \(\frac{10}{110} x\)
4. \(\frac{283}{383} x\)

Answer: 4. \(\frac{283}{383} x\)

Using equation,

PV = nRT

or \(\frac{P V}{M}=\frac{1}{M_0} R T\)

or \(\frac{P}{\rho} =\frac{R T}{M_0} \)

r = \(\frac{\rho}{P}=\frac{M}{R T}\)

∴ \(\frac{\rho}{P} \propto \frac{1}{T}\)

So, \(\frac{r_2}{r_1}=\frac{T_1}{T_2}=\frac{273+10}{273+110}=\frac{283}{383}\)

or \(r_2=\frac{283}{383} r_1\)

Question 5. The equation of state for 5 g of oxygen at a pressure P and temperature T, when occupying a volume V, will be (where R is the gas constant):

1. PV= (5/32)RT
2. PV= 5RT
3. PV= (5/2)RT
4. PV= (5/16)RT

Answer: 1. PV= (5/32)RT

We know that, PV = nRT

n=\(\frac{m}{\text { molecular mass }}=\frac{5}{32}\)

P V=\(\left(\frac{5}{32}\right) R T \)

Question 6. Three containers of the same volume contain three different gases. The masses of the molecules are m₁, m_2, and m₃ and the number of molecules in their respective containers are N₁, N_2, and N₃. The gas pressure in the containers is p₁, p_2, and p₃ respectively. All the gases are now mixed and put in one of these containers. The pressure p of the mixture will be:

1. \(p<\left(p_1+p_2+p_3\right)\)
2. p=\(\frac{p_1+p_2+p_3}{3}\)
3. p=\(p_1+p_2+p_3\)
4. \(p>\left(p_1+p_2+p_3\right)\)

Answer: 1. \(p<\left(p_1+p_2+p_3\right)\)

Given

Three containers of the same volume contain three different gases. The masses of the molecules are m₁, m_2, and m₃ and the number of molecules in their respective containers are N₁, N_2, and N₃. The gas pressure in the containers is p₁, p_2, and p₃ respectively. All the gases are now mixed and put in one of these containers.

According to Dalton’s law of partial pressure, the total pressure exerted by a mixture of gases that do not interact with each other is equal to the sum of the partial pressures that each would impose if alone occupied the same volume at the given temperature. When various gases are combined in one container, the mixture’s pressure P will be P=P₁+P₂+P₃

Question 7. A ideal gas equation can be written as:\(P=\frac{\rho R T}{M_0}\) where, ρ and M₀ are respectively :

1. mass density, the mass of the gas
2. number density, molar mass
3. mass density, molar mass
4. number density, the mass of the gas

Answer: 3. mass density, molar mass

The ideal gas equation is given by:

P V = nRT

P V =\(\frac{m}{\mathrm{M}} R T\)

P =\(\frac{m}{V}\left(\frac{R T}{M_0}\right)\)

P =\(\rho\left(\frac{R T}{M_0}\right)\)

∴ \(\mathrm{P} =\frac{m}{\mathrm{~V}}\)

Where, \(\rho \text { and } \mathrm{M}_{\mathrm{o}}\) are mass density and molar mass respectively.

Question 8. The average thermal energy for a monoatomic gas is (where Kg is Boltzmann constant and T is the absolute temperature.):

1. \(\frac{3}{2} K_B T\)
2. \(\frac{5}{2} K_B T\)
3. \(\frac{7}{2} K_B T\)
4. \(\frac{1}{2} K_B T\)

Answer: 1. \(\frac{3}{2} K_B T\)

The average thermal energy of the system with a degree of freedom is equal to its average energy.

Average thermal energy =\(\frac{f}{2} K_B \cdot T\)

For monoatomic gas f=3

Average thermal energy =\(\frac{3}{2} K_B \cdot T\)

Where, \(K_B\)= Boltzmann constant

and T = absolute temperature.

Question 9. An increase in the temperature of a gas-filled container would lead to:

1. increase in its kinetic energy
2. decrease in its pressure
3. decrease in intermolecular distance
4. increase in its mass.

Answer: 1. increase in its kinetic energy

An increase in the temperature of a gas-filled container leads to an increase in its kinetic energy.

Question 10. At what temperature will the RMS speed of oxygen molecules become just sufficient for escaping from the Earth’s atmosphere? Given : mass of oxygen molecule m= 2.76 x 10^-26 kg; Boltzmann’s constant kB= 1.38 x 10^-23Jk

1. 5.016 x 10⁴ K
2. 8.326 x 10⁴ K
3. 2.508 x 10⁴ K
4. 1.254 x 10⁴ K

Answer: 2. 8.326 x 10⁴ K

Escape velocity is the minimum velocity with which when a body is projected, so as to enable it to just overcome the gravitational pull of that surface i.e.Earth

Given: \(k_B =1.38 \times 10^{-23} \mathrm{Jk}^{-1}\)

⇒ \(m_0 =2.76 \times 10^{-26} \mathrm{~g}\)

Escape Velocity, \(v_e=\sqrt{\frac{2 G M}{R}}=\sqrt{2 g R}\)

⇒ \(v_e =\sqrt{2 \times 9.8 \times 6.4 \times 10^6}\)

=\(11.2 \mathrm{kms}^{-1}=11200 \mathrm{~ms}^{-1}\)

⇒ [Since radius of earth R=6.4 \(\times 10^6 \mathrm{~m}]\)

Say at temperature T it attains escape velocity

⇒ \(v_e =\sqrt{\frac{3 K_B T}{m_{02}}}\)

11200 =\(\sqrt{\frac{3 K_B T}{m_{02}}}\)

T =\(\frac{\left(11.2 \times 10^3\right)^2 \times 2.76 \times 10^{-26}}{3 \times 1.38 \times 10^{-23}}\)

∴ T =8.326 \(\times 10^4 \mathrm{k}\)

Question 11. The molecules of a given mass of a gas have r.m.s. velocity of 200 ms^-1 at 27°C and 1.0 x 10s Nm^-2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 x 105 Nm^-2, the RMS velocity of its molecules in ms^-1 is:

1. \(\frac{400}{\sqrt{3}}\)
2. \(\frac{100 \sqrt{2}}{3}\)
3. \(\frac{100}{3}\)
4. \(100 \sqrt{2}\)

Answer: 1. \(\frac{400}{\sqrt{3}}\)

Given, \(v_{\mathrm{rms}}=200 \mathrm{~ms}^{-1}, T_1=300 \mathrm{~K}, P_1=10_5 \mathrm{~N} / \mathrm{m}^2\)

⇒ \(T_2=400 \mathrm{~K}, P_2=0.05 \times 10^5 \mathrm{~N} / \mathrm{m}\)

We know that, \(v_{\text {rms }}=\sqrt{\frac{3 k_B T}{m}}\)

⇒ \(v_{\text {rms }} \propto \sqrt{T}\)

⇒  \(\frac{v_{27}}{v_{127}}=\sqrt{\frac{27+273}{127+273}}=\sqrt{\frac{300}{400}}=\frac{\sqrt{3}}{2}\)

∴ \(v_{\mathrm{rms}}=\frac{200 \times 2}{\sqrt{3}} \mathrm{~m} / \mathrm{s}=\frac{400}{\sqrt{3}} \mathrm{~m} / \mathrm{s}\)

Question 12. In a vessel, the gas is at pressure P, if the mass of all the molecules is halved of their speed is double, then the resultant pressure will be :

1. 2P
2. P
3. P/2
4. 4P

Answer: 1. 2P

The equation of pressure is, \(P=\frac{1}{3} \frac{m \mathrm{~N}}{V} v_{r m s}^2\)  Equation 1

where, m = mass of each molecule

N = number of molecules

Z = volume of the gas

According to the question: Mass of all molecules is halved and velocity is double then

⇒ \(P^{\prime} =\frac{1}{3}\left(\frac{m}{2}\right) \times \frac{N}{V} \times\left(2 v_{r m s}\right)^2 \)

=\(\frac{2}{3} \frac{m N}{V} v_{r m s}^2 \)

=\(2 \times \frac{1}{3} \frac{m \mathrm{~N}}{V} v_{r m s}^2\)

=2 P

compare with eq (1), P’ = 2P

Question 13. The pressure of a gas is raised from 27°C to 927°C. The root mean square speed:

1. Is\(\sqrt{\left(\frac{927}{27}\right)}\)times the earlier value
2. remains the same
3. gets halved
4. gets doubled

Answer: 3. gets halved

The square root of the mean of the squares of the random velocities of individual molecules in a gas is defined as RMS speed.

RMS speed is calculated by using the Maxwell distribution law \(C_{\mathrm{rms}}=\sqrt{\left(\frac{3 k T}{m}\right)}\)

⇒  \(C_{\mathrm{rms}} \propto \sqrt{T}\)

For two different cases i.e. at two different temperatures,

⇒  \(\frac{\left(C_{\text {rms }}\right)_1}{\left(C_{\text {rms }}\right)_2}=\sqrt{\frac{T_1}{T_2}}\)

Here, \(T_1=27^{\circ} \mathrm{C}=300 \mathrm{~K}\)

⇒  \(T_2=927^{\circ} \mathrm{C}=1200 \mathrm{~K}\)

⇒  \(\frac{\left(C_{\mathrm{rms}}\right)_1}{\left(C_{\mathrm{rms}}\right)_2}=\sqrt{\frac{300}{1200}}=\frac{1}{2}\)

⇒  \(\left(C_{\mathrm{rms}}\right)_2=2\left(C_{\mathrm{rms}}\right)_1\)

∴ Hence, the RMS speed will be doubled.

Question 14. The relation between pressure (p) and energy (E) of a gas is:

1. p=\(\frac{2}{3} E\)
2. p=\(\frac{1}{3} E\)
3. p=\(\frac{3}{2} E\)
4. p=3 E

Answer: 1. p=\(\frac{2}{3} E\)

We have, pressure exerted by gas molecules,

p=\(\frac{1}{3} \rho_{\mathrm{v}}^{-}\)  →  Equation 1

where, \(\rho\)= density of gas

⇒ \(\bar{v}\)= average velocity of gas molecules, or  \(p=\frac{2}{3} n \cdot \frac{1}{2} m_{\mathrm{v}} ( since \rho=mn)\)

Here, \(\frac{1}{2} m \overline{\mathrm{v}}\)= average kinetic energy of a gas molecule \((\overline{\mathrm{KE}})\)

Therefore,p=\(\frac{2}{3} n \overline{\mathrm{KE}}\)

If the total number of gas molecules in volume V is N then, Therefore, No. of gas molecules per unit volume

n = \(\frac{N}{V} \)

P = \(\frac{2}{3} \cdot \frac{N}{V}\left(\frac{1}{2} m v^2\right)\)

{or} P V = \(\frac{2}{3} N(\overline{\mathrm{KE}}) \quad\left[K E=\frac{1}{2} m v^2\right]\)

Also, from Eq. (1),

P V=\(\frac{2}{3} \cdot \frac{1}{2} \rho v^2\)

Here, \(\frac{1}{2} \rho v^{-2}\)= average kinetic energy of the gas per unit volume.

Therefore, P=\(\frac{2}{3} E\)

Question 15. According to the kinetic theory of gases, at absolute zero temperature:

1. water freezes
2. liquid helium freezes
3. molecular motion stops
4. liquid hydrogen freezes

Answer: 4. liquid hydrogen freezes

According to the kinetic theory of gases, the pressure P exerted by one mole of an ideal gas,

P = \(\frac{1}{3} \frac{M}{V} c^2\)

or \(\frac{1}{3} M c^2\)

or \(\frac{1}{3} M c^2=\mathrm{RT}\)  → Equation 1

where c is the root mean square velocity of gas. From (1), when T = 0, c = 0

Hence, the absolute zero temperature can be defined as the temperature at which the root mean square velocity of the gas molecules falls to zero. At absolute zero temperature, the molecular motion comes to a stop.

Question 16. Match Column – 1 and Column – 2 and choose the correct match from the given choices:

1. 1 – C,  2  – A,   3 – D,  4 -B
2. 1 – B,  2  –  C    3 – D, 4 – A
3. 1 – B,  2 – A,   3 – D, 4 – C
4. 1 – C,  2 – B,   3 – A,  4 – D

Answer: 3. 1 – B,  2 – A,   3 – D, 4 – C

The RMS velocity is, \(v_{r m s}=\sqrt{\frac{3 R T}{M}}\)

The pressure exerted by an ideal gas is \(\frac{1}{3} m n v^{-2}\).

Average kinetic energy of a molecule \(\frac{3}{2} k_B T\).

The total internal energy of 1 mole of a diatomic gas, U=\(\frac{5}{2} R T\).

Question 17. The volume ( V) of a monoatomic gas varies with its temperature (7), as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to B is:

1. \(\frac{1}{3}\)
2. \(\frac{2}{3}\)
3. \(\frac{2}{5}\)
4. \(\frac{2}{7}\)

Answer: 3. \(\frac{2}{5}\)

The given graph shows that Volume V \(\propto\) temperature

⇒ \(\frac{V}{T}\)= Constant

This is an isobaric process,

We know that Work done, \(\Delta W=P \Delta V=n R \Delta T\)  →  Equation 1

Absorbed heat, \(\Delta Q=n C_P D T=n C_p\left(T_B-T_A\right)\)  → Equation 2

For monoatomic gas, f=3

⇒ \(C_P=\left(R+\frac{3}{2} R\right)=\frac{5}{2} R\)

Then eq.(2) becomes,

⇒ \(\Delta \mathrm{Q}=n\left(\frac{5}{2} R\right)\left(T_B-T_A\right)\)  Equation 2

Divided eq. (1) by (2) we write,

⇒ \(\frac{\Delta \mathrm{W}}{\Delta \mathrm{Q}}=\frac{n R[T_B-T_A]}{n(\frac{5}{2}}\)

∴ \(R\left[T_B-T_A\right]=\frac{2}{5}\)

Question 18. A gas mixture consists of 2 moles of O₂ and 4 moles of Ar at temperature T. Neglecting all vibrational modes, the total internal energy of the system is:

1. ART
2. 15RT
3. 9RT
4. 11 RT

Answer: 4. 11 RT

Total internal energy of system = Internal energy of oxygen molecules + internal energy of argon molecules

= \(\frac{f_1}{2} \eta_1 R T+\frac{f_2}{2} \eta_2 R T\)

= \(\frac{5}{2} \times 2 R T+\frac{3}{2} \times 4 R T=11 R T\)

Question 19. A mass of diatomic gas (y = 1.4) at a pressure of 2 atm is compressed adiabatically so that its temperature rises from 27° C to 927° C. The pressure of the gas at the final state is:

1. 28 atm
2. 68.7 atm
3. 256 atm
4. 8 atm

Answer: 3. 256 atm

⇒ \(T_1=273+27=300 \mathrm{~K}\)

⇒ \(T_2=273+927=1200 \mathrm{~K}\)

for adiabatic process, \(P V^\gamma\) = constant

⇒ \(P\left(\frac{T}{P}\right)^\gamma\) = constant {because P V=n R T}

⇒ \(\frac{P_2}{P_1} =\left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\gamma-1}}\)

⇒ \(P_2 =P_1\left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\gamma-1}}\)

= \(2\left(\frac{1200}{300}\right)^{\frac{1.4}{1.4-1}}\)

= \((2)(4)^{\frac{1.4}{1.4-1}}\)

= 256 atm

Question 20. The gas carbon-monoxide (CO) and nitrogen (N₂) at the same temperature have kinetic energies E₁ and E₂ respectively. Then:

1. E₁ = E₂
2. E₁ > E₂
3. E₁ < E₂
4. E₁ and E₂ cannot be compared.

Answer: 1. E₁ = E₂

Since carbon monoxide (CO) and nitrogen (N₂) are diatomic gases. So, their kinetic energies will be equal, i.e. E₁ = E₂.

Question 21. An ideal gas at 27°C is compressed adiabatically to \(\frac{8}{27}\)of its original volume. The rise in temperature is [Given: \(\gamma=\frac{5}{3}\)

1. 475° C
2. 402° C
3. 275° C
4. 375° C

Answer: 4. 375° C

In an adiabatic process, \(P V^\gamma\)= constant  → Equation 1

Where, P= pressure, V= volume and \(\gamma\)= atomicity of gas,

Now from the ideal gas equation, P V=R T  (for one mole)

or P=\(\frac{R T}{V}\) (where, R= gas constant) →  Equation  2

From Eqs. (1) and (2), we get,

⇒ \(\left(\frac{R T}{V}\right) V^\gamma\) = constant

⇒ \(T V^{\gamma-1}\) = constant

For two different cases of temperature and volume of a gas,

⇒ \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)

or \(\frac{T_2}{T_1}=\left(\frac{V_1}{V_2}\right)^{\gamma-1}\)  →   Equation  3

Given, \(T_1 =27^{\circ} \mathrm{C}\)

= 27+273=300 \(\mathrm{~K}\)

And \(\frac{V_2}{V_1}=\frac{8}{27}\), \(\gamma=\frac{5}{3}\)

Substituting these values in Eq. (3), we get,

⇒ \(\frac{T_2}{300}=\left(\frac{27}{8}\right)^{5 / 3-1}\)

or \(\frac{T_2}{300}=\left[\left(\frac{3}{2}\right)^3\right]^{2 / 3}\)

or \(\frac{T_2}{300}=\left(\frac{3}{2}\right)^2=\frac{9}{4}\)

⇒ \(T_2=\frac{9}{4} \times 300=675 \mathrm{~K}=402^{\circ} \mathrm{C}\)

Thus, rise in temperature, = \(T_2-T_1\)

= \(402^{\circ} \mathrm{C}-27^{\circ} \mathrm{C}=375^{\circ} \mathrm{C}\)

Question 22. The degrees of freedom of a molecule of a triatomic gas are:

1. 2
2. 4
3. 6
4. 8

Answer: 3. 6

• A triatomic gas molecule tends to rotate along one of three coordinate axes. As a result, it possesses six degrees of freedom, 3 of which are translational and 3 of which are rotational.
• A triatomic molecule with a high enough temperature has 2 vibrational degrees of freedom. But, as there is no temperature requirement given. So, by simply assuming a triatomic gas molecule at room temperature has 6 degrees of freedom.
• Thus,(3 translational degrees + 3 rotational degrees) at room temperature.

Question 23. A diatomic gas initially at 18°C is compressed adiabatically to one-eight of its original volume. The temperature after compression will be:

1. 18° C
2. 668.4° K
3. 395.4° C
4. 144° C

Answer: 2. 668.4° K

⇒ \(T V^{\gamma-1}\)= constant

For two different cases, of temperature and volume of the gas.

⇒ \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)  →  Equation 1

Given, the initial temperature,

⇒ \(T_1=18^{\circ} \mathrm{C}=291 \mathrm{~K}\)

Let initial volume, \(V_1\)=V then the final volume, \(V_2=\left(\frac{1}{8}\right)\) V Given,

Putting these values in Eq. (1),

⇒ \(T_2 =291\left(\frac{V_1}{V_2}\right)^{\gamma-1}=291\left(\frac{V}{\left(\frac{1}{8}\right) V}\right)^{7 / 5-1}\)

= 668.4 \(\mathrm{~K}\)

Question 24. The number of translational degrees of freedom for a diatomic gas is:

1. 2
2. 3
3. 5
4. 6

Answer: 2. 3

Several degrees of freedom of a dynamical system is calculated by subtracting the number of independent relations from the total number of coordinates required to describe the positions of the system’s constituent particles.

If I is the number of particles in the system, R is the number of independent relations between the particles, and N is the system’s degree of freedom, then, N =3A – R

Every monoatomic, diatomic, and triatomic gas has three translational degrees of freedom

Question 25. The value of \(\left(\gamma=\frac{C_P}{C_V}\right)\)for hydrogen, helium and another
ideal diatomic gas X (whose molecules are not rigid but have an additional vibration mode), are respectively equal to :

1. \(\frac{7}{5}, \frac{5}{3}, \frac{9}{7}\)
2. \(\frac{5}{3}, \frac{7}{5}, \frac{9}{7}\)
3. \(\frac{5}{3}, \frac{7}{5}, \frac{7}{5}\)
4. \(\frac{7}{5}, \frac{5}{3}, \frac{7}{5}\)

Answer: 1. \(\frac{7}{5}, \frac{5}{3}, \frac{9}{7}\)

⇒ \(\gamma=\frac{C_P}{C_V}\)

where \(C_P\)= molar heat capacity constant pressure and \(C_V\)= molar heat capacity at constant volume Also, \(C_P=C_V+R\) (from Mayer’s relation)

⇒ \(C_V=\frac{f}{2} R\) (where, f= degree of freedom)

⇒ \(C_P=\left(\frac{f}{2}+1\right) R\)

So eq. (1) becomes,

⇒ \(\gamma=1+\frac{2}{f}\)

For hydrogen gas, which is diatomic, the degree of freedom is 5 (3 translational, 2 rotational).

⇒ \(\gamma=1+\frac{2}{5}=\frac{7}{5}\)

For helium gas, which is monatomic, the degree of freedom is 3 ( 3 translational only).

⇒ \(\gamma=1+\frac{2}{3}=\frac{5}{3}\)

The diatomic gas X also has vibrational motion, so the degree of freedom is 7 (3 translational, 2 rotational, and 2 vibrational)

∴ \(\gamma=1+\frac{2}{7}=\frac{9}{7}\)

Question 26. One mole of an ideal monatomic gas undergoes a process described by the equation pV₃ =constant. The heat capacity of the gas during this process is:

1. \(\frac{3}{2} R\)
2. \(\frac{5}{2} R\)
3. 2R
4. R

Answer: 4. R

From the polytropic process,

⇒ \(P V^x\)= constant

Heat capacity in the polytropic process is given by,

C=\(C_y+\frac{R}{1-x}\)

From question, \(\mathrm{PV}^3\) = constant

x = 3  →  Equation 1

and also gas is monoatomic,

So,\(C_V=\frac{3}{2} R \)  →  Equation 2

from above formula, C =\(\left[\frac{3}{2} R+\frac{R}{1-3}\right]\)

=\(\frac{3}{2} R-\frac{R}{3}\)=R

Question 27. The ratio of the specific heat \(\frac{C_P}{C_V}=\gamma\) in terms of degrees of freedom (n) is given by:

1. \(\left(1+\frac{1}{n}\right)\)
2. \(\left(1+\frac{n}{3}\right)\)
3. \(\left(1+\frac{2}{n}\right)\)
4. \(\left(1+\frac{n}{2}\right)\)

Answer: 3. \(\left(1+\frac{2}{n}\right)\)

We know that specific heat at constant volume is given by,\(C_V=\frac{n}{2} R\)

Where, n = degree of freedom

R = gas constant

And \(C_P-C_V\)=R  [Mayer’s formula]

⇒\(C_P=\frac{n}{2} R+R=R\left(1+\frac{n}{2}\right)\)

⇒ \(\gamma=\frac{C_P}{C_V}=\frac{R\left(1+\frac{n}{2}\right)}{\frac{n}{2} R}\)

= \(\frac{2}{n}+1 \)

Question 28. The molar-specific heats of an ideal gas at constant pressure and volume and denoted by Cp and Cv respectively.  If \(\gamma=\frac{C_P}{C_V}\) and R is the universal gas constant then Cv is equal to:

1. \(\frac{1+\gamma}{1-\gamma}\)
2. \(\frac{R}{(\gamma-1)}\)
3. \(\frac{(\gamma-1)}{R}\)
4. \(\gamma^R\)

Answer: 2. \(\frac{R}{(\gamma-1)}\)

As we know, \(C_P-C_V\) = R and \(\gamma=\frac{C_P}{C_V}\)

⇒ \(C_V =\frac{\mathrm{R}}{\gamma-1}\)

Question 29. The amount of heat energy required to raise the temperature of 1 g of helium at NTP, from T₁K to T₂K is:

1. \(\frac{3}{8} N_a k_B\left(T_2-T_1\right)\)
2. \(\frac{3}{2} N_a k_B\left(T_2-T_1\right)\)
3. \(\frac{3}{4} N_a k_B\left(T_2-T_1\right)\)
4. \(\frac{3}{4} N_a k_B\left(\frac{T_2}{T_1}\right)\)

Answer: 1. \(\frac{3}{8} N_a k_B\left(T_2-T_1\right)\)

Number of moles of 1 \(\mathrm{~g} \mathrm{He}=\frac{1}{4}\)

The amount of heat energy required to raise the temperature of the gas is,

⇒ \(\Delta \mathrm{Q}=n \mathrm{C}_{\mathrm{V}} \Delta \mathrm{T}\)

Here, n=\(\frac{1}{4}, C_V =\frac{3}{2} R\)

= \(\left(\frac{1}{4}\right)\left(\frac{3}{2} R\right)\left(T_2-T_1\right)\)

= \(\frac{3}{8} k_B N_A\left(T_2-T_1\right) . (k_3=\frac{R}{N a})\)

Question 30. The molar specific heat at constant pressure of an ideal gas is (7/2) R. The ratio of specific heat at constant pressure to that at constant volume is:

1. 9/7
2. 7/5
3. 8/7
4. 5/7

Answer: 2. 7/5

Molar-specific heat at constant pressure,

⇒ \(C_P=\frac{7}{2} R\)

We know that, \(C_P-C_V=R\)

⇒ \(C_V =C_P-R \)

= \(\frac{7}{2} R-R=\frac{5}{2} R\)

from (1) and (2),

∴ \(\frac{C_P}{C_V}=\frac{7}{5}\)

Question 31. One mole of an ideal gas at an initial temperature of TK does 6R joules of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be:

1. (T+2X)K
2. {T-2A)K
3. (T+4)K
4. (T-4)K

Answer: 1. (T+2X)K

We know that work done in the adiabatic process is:

W=\(\frac{-1}{V-1}\left(P_f V_f-P_i V_i\right)\)

⇒ \(6 R=\frac{-1}{\frac{5}{3}-1} R\left(T_f-T_i\right)\)  {Since,P V=n R T}

⇒ \(T_f-T_i=-4\)

∴ \(T_f=(T-4) \mathrm{K}\)

Question 32. If for a gas, \(\frac{R}{C_{\mathrm{v}}}\)= 0.67, this gas is made up of molecules which are:

1. diatomic
2. mixture of diatomic and polyatomic molecules
3. monoatomic
4. polyatomic

Answer: 3. monoatomic

Since, \(C_{\mathrm{v}}=\frac{R}{0.67} \approx 1.5 R=\frac{3}{2} R\)

Hence, it is the case of monoatomic gases

Question 33. For hydrogen gas Cp – Cv = a and oxygen gas C_p – C_v = b, the relation between a and b is given by:

1. a= 16b
2. 16b = a
3. a = 4b
4. a = b

Answer: 4. a = b

Since hydrogen and oxygen are diatomic gases and C_p – C_v = R is the same for all gases. Hence, a: b, assuming C_p and C_v are gram molar specific heats.

Question 34. For a certain gas, the ratio of specific heat is given to be y = 1.5, for this gas:

1. \(C_v=\frac{3 R}{J}\)
2. \(C_p=\frac{3 R}{J}\)
3. \(C_p=\frac{5 R}{J}\)
4. \(C_p=\frac{5 R}{J}\)

Answer: 2. \(C_p=\frac{3 R}{J}\)

We have,\(\gamma=\frac{C_P}{C_V}\)

Given,\(\gamma=1.5=\frac{3}{2}\)

⇒ \(C_V=\frac{2}{3} C_P\)

From Mayer’s formula, \(C_P-C_V =\frac{R}{J}\)

⇒ \(C_P-\frac{2}{3} C_P =\frac{R}{J}\)

⇒ \(\frac{C_P}{3} =\frac{R}{J}\)

∴ \(C_P =\frac{3 R}{J}\)

Question 35. At 27°C a gas is compressed suddenly such that its pressure becomes \(\left(\frac{1}{8}\right)\)of original pressure. Final temperature will be \(\left(\gamma=\frac{5}{3}\right)\)

1. 420 K
2. 300 K
3. -142° C
4. 327 K

Answer: 3. -142° C

In an adiabatic process, PVϒ = k(a constant)  →  Equation 1

where, P = pressure and V = volume and ϒ =atomicity of gas

Again from standard gas equation,\(P V^\gamma =n R T\)

V =\(\frac{R T}{P}\)

Putting the value of V in Eq. (1), we get

⇒ P \(\frac{R^\gamma T^\gamma}{p^\gamma}\)=k or

⇒ \(P^{1-\gamma} T^\gamma=\frac{k}{R^\gamma}\)= another constant or

⇒ \(P^{1-\gamma} T^\gamma\)= constant

For two different cases,

⇒ \(P_1{ }^{1-\gamma} T_1{ }^\gamma=P_2{ }^{1-\gamma} T_2{ }^\gamma\)

⇒ \(\left(\frac{T_2}{T_1}\right)^\gamma =\left(\frac{P_1}{P_2}\right)^{1-\gamma}\)

Here, \(P_2 =\left(\frac{1}{8}\right) P_I\)

⇒ \(T_1 =27^{\circ} \mathrm{C}=273+27=300 \mathrm{~K}\)

⇒ \(T_2 =?, \gamma=\frac{5}{3}\)

⇒ \(\left(\frac{T_2}{300}\right)^{5 / 3} =(8)^{1-5 / 3}=(8)^{-2 / 3}\)

⇒ \(T_2 =130.6 \mathrm{~K}\)

∴\(T_2 =-142^{\circ} \mathrm{C}\)

Question 36. The mean free path X for a gas, with molecular diameter d and number density n, can be expressed as:

1. \(\frac{1}{\sqrt{2} n \pi d^2}\)
2. \(\frac{1}{\sqrt{2} n^2 \pi d^2}\)
3. \(\frac{1}{\sqrt{2} n^2 \pi^2 d^2}\)
4. \(\frac{1}{\sqrt{2} n \pi d}\)

Answer: 1. \(\frac{1}{\sqrt{2} n \pi d^2}\)

The mean free path \(\lambda\) for gas, with molecular diameter d and number density n can be expressed on \(\frac{1}{\sqrt{2} n \pi d^2}\)

Question 37. The mean free path of a molecule of a gas (radius r) is inversely proportional to the:

1. \(r^3\)
2. \(r^2\)
3. r
4. \(\sqrt{r}\)

Answer: 2. \(r^2\)

Mean free path, \(\lambda=\frac{1}{\pi n r^2}\)

∴ \(\lambda \propto \frac{1}{r^2}\)

Question 38. At constant volume, temperature is increased, then:

1. collision on walls will be less.
2. the number of collisions per unit of time will increase.
3. collisions will be in straight lines.
4. collisions will not change.

Answer: 2. the number of collisions per unit of time will increase.

The average velocity of the gas molecules increases as the temperature rises. As a result, more molecules collide with the walls. Hence, the number of collisions per unit time will increase.

Question 39. A polyatomic gas with n degrees of freedom has a mean energy per molecule given by:

1. \(\frac{n k T}{N}\)
2. \(\frac{n k T}{2 N}\)
3. \(\frac{n k T}{2}\)
4. \(\frac{3 k T}{2}\)

Answer: 3. \(\frac{n k T}{2}\)

According to the law of energy equipartition, for any dynamical system in thermal equilibrium, the total energy is distributed equally across all degrees of freedom, and the energy associated with each molecule per degree of freedom equals 12kT. The mean energy per molecule for a polyatomic gas with n degrees of freedom is \(\frac{1}{2} n k T\).

Where,k = Boltzmann

constant n = degree of freedom,

and T- Temperature

NEET Physics For Thermodynamics Multiple Choice Questions

Question 1. A sample of 0.1 g of water at 100° C and normal pressure (1.013 x 10⁵ Nm^-2) requires 54 cal of heat energy to convert to steam at 100°C. If the volume of the steam produced is 167.1 cc, the change in internal energy of the sample is:

1. 42.2 J
2. 208.7 J
3. 104.3 J
4. 84.5 J

Answer: 2. 208.7 J

Given

A sample of 0.1 g of water at 100° C and normal pressure (1.013 x 10⁵ Nm^-2) requires 54 cal of heat energy to convert to steam at 100°C. If the volume of the steam produced is 167.1 cc,

From the question, Heat spent during the conversion of a sample of water at \(100^{\circ}\) to steam is,

⇒ \(\Delta \mathrm{Q} =54 \mathrm{cal}=54 \times 4.18 \mathrm{~J}=225.72 \mathrm{~J}\)

⇒ \(P =1.013 \times 10^5 \mathrm{Nm}^{-2}\)

Work done \(\Delta W=P \Delta V=P\left[V_{\text {steam }}-V_{\text {water }}\right]\)

Here, \(V_{\text {steam }}=|167| c c=1 \times 10^{-6} \mathrm{~m}^3\)

⇒ \(V_{\text {water }} =0.1 \mathrm{~g}=0.1 c c=0.1 \times 10^{-6} \mathrm{~m}\)

⇒ \(\Delta W =1.013 \times 10^5\left[(167.1-0.1) \times 10^{-6}\right]\)

=\(1.013 \times 167 \times 10^{-1}=(16.917)\)

We also know that,

⇒ \(\Delta Q =\Delta U+\Delta W\)

⇒ \(\Delta U =\Delta Q-\Delta W=2.25 .72-16.917\)

=208.75

Question 2. Liquid oxygen at 50 K is heated to 300 K at a constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?

Answer: 1.

The given graph in option (1) shows the variation of temperature with time.

Question 3. The internal energy change in a system that has absorbed 2 KCal of heat and done 500 J of work is:

1. 8900 J
2. 6400 J
3. 5400 J
4. 7900 J

Answer: 4. 7900 J

Using the first law of thermodynamics, \(\Delta U=\Delta Q-\Delta W\)

ΔU = ΔQ-ΔW

= 2 x 4.2 x 1000-500 = 8400 – 500 = 7900 J

Read and Learn More NEET Physics MCQs

Question 4. 110 J of heat is added to a gaseous system, whose internal energy is 40 J, then the amount of external work done is:

1. 150 J
2. 70 J
3. 110 J
4. 40 J

Answer: 2. 70 J

From the first law of thermodynamics,

⇒ \(\Delta Q=\Delta U+\Delta W\)

where, \(\Delta Q\)= heat given

⇒ \(\Delta U\)= change in internal energy

⇒ \(\Delta W\)= work done

Here,\(\Delta Q = 110 \mathrm{~J}\)

⇒ \(\Delta U =40 \mathrm{~J}\)

⇒ \(\Delta W =\Delta Q-\Delta U\)

=110-40=70 \(\mathrm{~J}\)

Question 5. The first law of thermodynamics is a consequence of the conservation of:

1. work
2. energy
3. heat
4. All of these

Answer: 2. energy

According to the first law of thermodynamics, when some amount of heat (dQ) is supplied to a system capable of doing external work, the amount of heat absorbed by the system (dQ) equals the sum of the increase in the internal energy of the system (dU) due to temperature rise and the external work done by the system (dW) in expansion.

dQ =dU + dW

This law is the law of conservation of energy that applies to every process in nature.

Question 6. One mode of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. The change in internal energy of the gas during the transition is:

1. 20 J
2. -12 kJ
3. 20 kJ
4. -20 kJ

Answer: 4. -20 kJ

We know, \(\Delta U=n C_V+\Delta T\)

= \(\mathrm{n}\left(\frac{5 \mathrm{R}}{2}\right)\left(\mathrm{T}_{\mathrm{B}}-\mathrm{T}_{\mathrm{A}}\right) \quad\left[\text { for diatomic, } \mathrm{CV}=\frac{5 \mathrm{R}}{2}\right]\)

= \( \frac{5 \mathrm{nR}}{2}\left(\frac{\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}}{\mathrm{nR}}-\frac{\mathrm{P}_{\mathrm{A}} \mathrm{V}_{\mathrm{A}}}{\mathrm{nR}}\right)\mathrm{PV}=\mathrm{nRT}]\)

= \(\frac{5}{2}\left(\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}-\mathrm{P}_{\mathrm{A}}-\mathrm{V}_{\mathrm{A}}\right)=\frac{5}{2}\left(2 \times 10^3 \times 6-5 \times 10^3 \times 4\right)\)

=\(\frac{5}{2}\left(-8 \times 10^3\right)=20 \mathrm{~kJ}\)

=\(n\left(\frac{5 R}{2}\right)\left(T_B-T_A\right)\) [for diatomic gas, \(\mathrm{Cv}\)=0

Question 7. If \(C_P\) and \(C_V\) denote the specific heats per unit mass of and ideal gas of molecular weight M, then

1. \(C_{P-} C_{V=R / M}{ }^2\)
2. \(C_P-C_{V=R}\)
3. \(C_{P-} C_{V=R / M}\)
4. \(C_{P-} C_{V=M R}\)

Where R is the molar gas constant.

Answer: 3. \(C_{P-} C_{V=R / M}\)

Let \(C_V\) and \(C_P \)be molar-specific heats of the ideal gas at constant volume and constant pressure, respectively, and then

⇒ \(\mathrm{C}_{\mathrm{P}}=\mathrm{MC}_{\mathrm{p}} \text { and } \mathrm{C}_{\mathrm{V}}=\mathrm{MC}_{\mathrm{V}}\)

⇒ \(\mathrm{C}_{\mathrm{P}}-\mathrm{C}_{\mathrm{V}}=\mathrm{R}\)

⇒ \(\mathrm{MC}_{\mathrm{P}}-\mathrm{MC}_{\mathrm{V}}=\mathrm{R}\)

∴ \(\mathrm{C}_{\mathrm{P}}-\mathrm{C}_{\mathrm{V}}=\mathrm{R} / \mathrm{M}\)

Question 8. If the ratio of the specific heat of a gas at constant pressure to that of the constant volume is y, the change in internal energy of a mass of gas when the volume changes from V to 2V at constant pressure P is:

1. \(\frac{R}{(\gamma-1)}\)
2. PV
3. \(\frac{P V}{(\gamma-1)}\)
4. \(\frac{\gamma P V}{(\gamma-1)}\)

Answer: 3. \(\frac{P V}{(\gamma-1)}\)

Change in internal energy of a gas having atomicity \(\gamma\) is given by,

⇒ \(\Delta U=\frac{1}{(\gamma-1)}\left(p_2 V_2-p_1 V_1\right)\)

Given,\(V_1=V, V_2=2 V\)

So,\(\Delta U =\frac{1}{\gamma-1}[p \times 2 V-p x V]\)

= \(\frac{1}{\gamma-1} p V=\frac{p V}{\gamma-1}\)

Question 9. One mole of an ideal gas requires 207 J heat to raise the temperature by 10 K when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same 1 K, the heat required is:

1. 198.7 J
2. 29 J
3. 215.3 J
4. 124 J

Answer: 4. 124 J

Using \(C_p-C_v=R,\)

⇒ \(\mathrm{C}_{\mathrm{p}}\) is heat needed for raising by 10 \(\mathrm{~K}\).

⇒ \(\mathrm{C}_{\mathrm{p}}=20.7 \mathrm{~J} / \mathrm{mole} \mathrm{K}\)

Given R = 8.3 J/mole K

For raising by 10 K = 124 J

Question 10. A cylinder contains hydrogen gas at a pressure of 249 kPa and temperature 27°C. Its density is (R = 8.3 J mol^-1 k^-1):

1. 0.5 kg / m³
2. 0.2 kg / m³
3. 0.1 kg / m³
4. 0.2 kg / m³

Answer: 2. 0.2 kg / m³

Given: \(\mathrm{P}=249 \mathrm{kPa} ; \mathrm{T}=27^{\circ} \mathrm{C}, \mathrm{M}=2 \times 10^{-3} \mathrm{~kg}\)

Equation of state,

P V=\(\eta R T or P M=\delta \mathrm{RT} \quad\left[\eta=\frac{m}{M}\right]\)

⇒ \(\delta =\frac{P M}{R T}\)

= \(\frac{\left(249 \times 10^3\right)\left(2 \times 10^{-3}\right)}{8.3 \times 300}=0.2 \mathrm{~kg} / \mathrm{m}^3\)

Question 11. Which of the following is not a thermodynamical function?

1. Enthalpy
2. Work done
3. Gibb’s energy
4. Internal energy

Answer: 2. Work done

• Certain specific thermodynamic variables, such as pressure p, volume V, temperature T, and entropy S, can be used to describe the thermodynamic state of a homogeneous system.
• Any two of these four variables are independent and once they’re known, the others can be calculated. As a result, there are just two independent variables, with the others working as functions.
• Certain relationships are essential for a thorough understanding of the system, and we introduce some thermodynamic functions, which are functions of variables p, V, T, and S. Thermodynamic functions are classified into four categories.

1. Internal energy (U)
2. Helmholtz tunction (F)
3. Enthalpy (H)
4. Gibb’s energy (G)

Hence, the work done is not a thermodynamic function

Question 12. An ideal gas undergoes four different processes at the same initial state as shown in the figure below. These processes are adiabatic, isothermal, isobaric, and isochoric. The curve which represents the adiabatic process among 1,2, 3, and 4 is:

1. 1
2. 2
3. 3
4. 4

Answer: 2. 2

Curve 4 is an isobaric process because the pressure is constant. Curve I is isochoric because the volume is constant. Curve 3 is smaller than curve 2.

Question 13. In which of the following processes, heat is neither absorbed nor released by a system?

1. Adiabatic
2. Isobaric
3. Isochoric
4. Isothermal

Answer: 1. Adiabatic

In an adiabatic process, there is no exchange of heat of the system with its surroundings. Thus in the adiabatic process P₁V₁ and T change but ΔQ = 0 or entropy remains a constant process, I – Isochoric, volume is constant\(\left(\Delta S=\frac{\Delta Q}{T}\right)\)

Question 14. Thermodynamic processes are indicated in the following diagram:

Match The Following:

1. P → A, Q → C, R → D, S → B
2. P → C, Q → A, R → D, S → B
3. P → C, Q → D, R → B, S → A
4. P → D ,Q → B, R → A, S → C

Answer: 1. P → A, Q → C, R → D, S→ B

Process, 1 – Isochoric, volume is constant.

2: Adiabatic, the slope of curve II is more than the slope of curve 3

3: Isothermal

4: Isobaric, Pressure is constant. repeat

Question 15. The volume (V) of a monatomic gas varies with its temperature (7), as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to state B, is:

1. \(\frac{2}{5}\)
2. \(\frac{2}{3}\)
3. \(\frac{1}{3}\)
4. \(\frac{2}{7}\)

Answer: 1. \(\frac{2}{5}\)

In the process 1, volume is constant.

Process 1 → Isochoric; P → C

As slope of curve 2 is more than the slope of curve III.

Process 2 → Adiabatic and

Process 3 -→ Isothermal

Q → A, R→D

In process 4, pressure is constant.

Process 4 → Isobaric; S → B

Question 16. A gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then:

1. compressing the gas through adiabatic.
2. compressing the gas isothermally or adiabatically will require the same amount of work.
3. which of the cases (whether compression through . isothermal or through an adiabatic process) requires more work will depend upon the atomicity of the gas.
4. compressing the gas isothermally will require more to be done.

Answer: 2. compressing the gas isothermally or adiabatically will require the same amount of work.

⇒ \(\mathrm{W}_{\text {ext }} =\text { negative of area with volume }- \text { axis }\)

∴ \(W(\text { adiabatic }) >W \text { (isothermal })\)

Question 17. The figure below shows two paths that may be taken by a gas to go from a state A to a state C. In process AB, 400 J of heat is added to the system, and in process, BC, 100 J of heat is added to the system. The heat absorbed by the system in process AC will be:

1. 380 J
2. 500 J
3. 460 J
4. 300 J

Answer: 3. 460 J

Given

The figure below shows two paths that may be taken by a gas to go from a state A to a state C. In process AB, 400 J of heat is added to the system, and in process, BC, 100 J of heat is added to the system.

From the diagram, We see that the initial and final points are the same.

Case 1 :

So, \(\Delta U_{A \rightarrow B \rightarrow C}=\Delta U_{A \rightarrow C}\) →  Equation 1

A \(\rightarrow B \)(Isochoric process)

⇒ \(d \mathrm{~W}_{\mathrm{A} \rightarrow \mathrm{B}}\)=0 and

⇒ \(d \mathrm{Q}=d \mathrm{U}=d \mathrm{~W}\)

∴ \(d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{B}}=d \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{B}}=400 \mathrm{~J}\)

Case 2 : \(\mathrm{B} \rightarrow \mathrm{C}\) is isobaric process

⇒ \(d \mathrm{Q}_{\mathrm{B} \rightarrow \mathrm{C}} =d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}+d \mathrm{~W}_{\mathrm{B} \rightarrow \mathrm{C}}\)

= \(d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}+\mathrm{P} \Delta \mathrm{V}_{\mathrm{B} \rightarrow \mathrm{C}}\)

⇒ \(100 =d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}+6 \times 10^4\left(2 \times 10^{-3}\right)\)

∴ \(d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}} =100-120=-20 \mathrm{~J}\)

Using eq. (1),

⇒ \(\Delta \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C}}=\Delta \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{C}}\)

⇒ \(\Delta \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{B}}+\Delta \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}\)

= \(d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{C}}-\mathrm{dW}_{\mathrm{A} \rightarrow \mathrm{C}}\)

⇒ \(400+(-20)=d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{C}}-\left(\mathrm{P} \Delta \mathrm{U}_{\mathrm{A}}+\text { Area } \Delta_{\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C}}\right)\)

⇒ \(d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{C}}=380[2 \times 10^4 \times 2 \times 10^{-3}+\).

⇒ \(\left.\frac{1}{2} \times 2 \times 10^{-3} \times 4 \times 10^4\right]\)

∴ \(d Q_{\mathrm{A} \rightarrow \mathrm{C}}=460 \mathrm{~J}\)

Question 18. A thermodynamic system undergoes the cyclic process ABCD as shown in the figure. The work done by the system in the cycle is:

1. \(p_0 V_0\)
2. \(2 p_0 V_0\)
3. \(\frac{p_0 V_0}{2}\)
4. zero

Answer: 4. zero

According to the question,

Work done in the cyclic process: Area bound by the closed configuration

Area of closed configuration \(\left\{2\left[\frac{1}{2}\left(\frac{\mathrm{V}_0}{2}\right) \times \mathrm{P}_0\right]+\left[-2\left\{\frac{1}{2}\left(\frac{\mathrm{V}_0}{2}\right) \times \mathrm{P}_0\right\}\right]\right\}=0\)

Question 19. An ideal gas is compressed to half its initial volume using several processes. Which of the processes results in the maximum work done on the gas?

1. Adiabatic
2. Isobaric
3. Isochoric
4. Isothermal

Answer: 1. Adiabatic

Work done = Area under P-V graph So large work is in adiabatic Here,

∴ \(W_{\text {adiabatic }}>W_{\text {isothermal }}>W_{\text {isobaric }}\)

Question 20. A Monoatomic gas at a pressure p, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is (take \(\lambda=\frac{5}{3}\)):

1. 64p
2. 32p
3. \(\frac{P}{64}\)
4. 16p

Answer: 3. \(\frac{P}{64}\)

Using Ideal Gas Equation, P =\(\frac{n R T}{V}\)

⇒ \(P_1 =\frac{n R T}{2 V}=\frac{P}{2}\)

For isothermal expansion, \(P V =P_1 \times 2 V \)

⇒ \(P_1 =\frac{P}{2}\)

For adiabatic expansion, \(P V^r\) = Constant

⇒ \(P_1 V_1^r= P_2 V_2^r\)

⇒ \(P_2 =[2 V]^{5 / 3}=P_2[16]^{5 / 3} \)

⇒ \(P^2 =\frac{P}{2}\left[\frac{2 V}{16 V}\right]^{\frac{5}{3}}=\frac{P}{2}\left[\frac{1}{8}\right]^{\frac{5}{3}}\)

= \(\frac{P}{2} \times 0.0312=0.0156 P\)

=  \(\frac{P}{64}\)

Question 21. A gas is taken through the cycle A →  B → C → A as shown. What is the net work done by the gas?

1. 200J
2. 1000J
3. Zero
4. -200J

Answer: 2. 1000J

Net work done = Area of triangle

= \(\frac{1}{2} \times\left[(7-2) \times 10^{-3}\right]\left[(6-2) \times 10^5\right] =1000 \mathrm{~J}\)

Question 22. During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its temperature.
The ratio of \(\frac{C_P}{C_V}\) for the gas is:

1. \(\frac{4}{3}\)
2. 2
3. \(\frac{5}{3}\)
4. \(\frac{3}{2}\)

Answer: 4. \(\frac{3}{2}\)

According to the question, \(P T^{-3}\)= Constant  →  Equation 1

For an adiabatic process, \(PT \|-r\)= constant  →   Equation 2

compare equation (1) and (2), we get

⇒ \(\frac{r}{1-r}=-3\)

r =\(-3+3 r \text { or } r=\frac{3}{2}\)

As, r =\(\frac{C_P}{C_V}\):

∴ \(\mathrm{C}_{\mathrm{P}} / \mathrm{C}_{\mathrm{V}} =\frac{3}{2}\)

Question 23. A system is taken from state a to state c by two paths act and abc as shown in the figure. The internal energy a is U₂ – 10 J. Along the path adc the amount of heat absorbed is δQ₁ = 50 J, and the work obtained δW₁ = 20 J whereas, along the path ABC, the heat absorbed δQ₂ = 36 J. The amount of work along the path ABC is:

1. 10 J
2. 12 J
3. 36 J
4. 6 J

Answer: 4. 6 J

Given

A system is taken from state a to state c by two paths act and abc as shown in the figure. The internal energy a is U₂ – 10 J. Along the path adc the amount of heat absorbed is δQ₁ = 50 J, and the work obtained δW₁ = 20 J whereas, along the path ABC, the heat absorbed δQ₂ = 36 J.

According to \(1^{\text {st }}\) law of thermodynamics

⇒ \(\delta Q=\delta V+\delta W\)

Along the path adc, \(\delta U_1=\delta Q_1-\delta W_1\)

=50-20

= 30 \(\mathrm{~J}\)

then path ABC , \(\delta U_2=36-\delta W_2\)

Since the change in Internal energy in path independence

So,\(\delta U_1 =\delta U_2\)

⇒ \(30 \mathrm{~J} =36 \mathrm{~J}-\delta W_2\)

⇒ \(\delta W_2 =36 \mathrm{~J}-30 \mathrm{~J} \)

=6 \(\mathrm{~J}\)

Question 24. Which of the following relations does not give the equation of an adiabatic process, where terms have their usual meaning?

1. \(P^{1-\gamma} T^\gamma\)= constant
2. \(P V^\gamma\)= constant
3. \(T V^{\gamma-1}\)= constant
4. \(P^\gamma T^{1-\gamma}\)= constant

Answer: 4. \(P^\gamma T^{1-\gamma}\)= constant

Adiabatic process \(\rightarrow \)Heat does not exchange between system surrounding

⇒ \(P V^\gamma\)= constant →  Equation 1

Ideal gas equation P V=n R T

P =\(\frac{n R T}{V}=\frac{n R T}{V} \quad V^\gamma\)= constant

⇒ \(T V^\gamma-1\) = constant  →  Equation 2

PV = nRT

V =\(\frac{n R T}{P}\) { Put in eq. (1) }

Again PV=n R T

⇒ \(P\left(\frac{n R T}{P}\right)^\gamma\) = constant

⇒ \(P^{1-\gamma} T^\gamma\) = constant

So, option (d) does not give the relation.

Question 25. A thermodynamic system is taken through the cycle ABCD as shown in the figure. Heat rejected by the gas during the cycle is:

1. 2 PV
2. 4 PV
3. \(\frac{1}{2} P V\)
4. PV

Answer: 1. 2 PV

From the question,

For a given cyclic process AV= 0

Q = W

W =- Area enclosed in the curve

= AB AD

= (2P-P) x (3V- V)

=-p x 2V

Heat rejected = 2 PV

Question 26. An ideal gas goes from state A to state B via three different processes as indicated in the p-V diagram. If Q₁, Q₂, Q₃ indicate the heat absorbed by the gas along the three processes and ΔU₁, ΔU₂, ΔU₂ indicate the change in internal energy along the three processes respectively, then:

1. Q₁ > Q₂ > Q₃ and ΔU₁ = ΔU₂ = ΔU₃
2. Q₃ > Q₂ > Q₁ and ΔU₁ = ΔU₂ = ΔU₃
3. Q₁ = Q₂ = Q₃ and ΔU₁ > ΔU₂ > ΔU₃
4. Q₃ > Q₂ > Q₁ and ΔU₁ > ΔU₂ > ΔU₃

Answer: 1. Q₁ > Q₂ > Q₃ and ΔU₁ = ΔU₂ = ΔU₃

Given

An ideal gas goes from state A to state B via three different processes as indicated in the p-V diagram. If Q₁, Q₂, Q₃ indicate the heat absorbed by the gas along the three processes and ΔU₁, ΔU₂, ΔU₂ indicate the change in internal energy along the three processes respectively,

According to the question,

⇒ \(\Delta U_1=\Delta U_2=\Delta U_3\)

⇒ \(Q_1>Q_2>Q_3\)

because, \(\Delta Q=\Delta W+d U\)

change in internal energy is independent of the path.

Question 27. One mole of an ideal gas goes from an initial state A to a final state B via two processes: It first undergoes isothermal expansion from volume V to 3 V and then its volume is reduced from 3V to V to constant pressure. The correct PL-V diagram representing the two processes is

Answer: 4.

Given that, gas A → B

firstly isothermal expansion = V to 3 V

then volume reduced from 3 V to V at constant pressure

(1) For isothermal expansion,

T= constant

PV= NRT = constant

PV= constant

Hence hyperbolic curve

(2) Now for isobaric compression,

P = constant

PV= nRT

∴ straight line. Hence option (D) is correct.

Question 28. During an isothermal expansion, a confined ideal gas does – 150 J of work against its surroundings. This implies that:

1. 150 J of heat has been removed from the gas.
2. 300 J of heat has been added to the gas
3. No heat is transferred because the process is isothermal.
4. 150 J of heat has been added to the gas.

Answer: 3. No heat is transferred because the process is isothermal

From the first law of thermodynamics

⇒ \(\Delta U=\Delta \mathrm{Q}+\Delta W\)

for isothermal process \(\Delta U\)=0

⇒ \(\Delta \mathrm{Q}=-\Delta W \)

⇒ \(\Delta Q\)=-(-150)=150

∴ Here \(\Delta\) Q is positive means heat is added to gas.

Question 29. A mass of diatomic gas (γ = 1.4) at a pressure of 2 atmospheres is compressed adiabatically so that its temperature rises from 27°C to 927°C. The pressure of the gas in the final state is:

1. 8 at
2. 28 atm
3. 68.7 atm
4. 256 atm

Answer: 4. 256 atm

For an adiabatic process, \(\frac{T^\gamma}{P^{\gamma-1}}\)= constant

⇒ \(\left(\frac{T_i}{T_f}\right)^\gamma=\left(\frac{P_i}{P_f}\right)^{\gamma-1}\)

Here,\( P_f=P_i\left(\frac{T_i}{T_f}\right)^{\frac{\gamma}{\gamma-1}}\)

⇒ \(\mathrm{~T}_{\mathrm{i}}=27^{\circ} \mathrm{C}=300 \mathrm{~K}\),

⇒ \(\mathrm{~T}_{\mathrm{f}}=927^{\circ} \mathrm{C}=1200 \mathrm{~K}\)

⇒ \(\mathrm{P}_{\mathrm{i}}=2 \mathrm{~atm}, \gamma\) = 1.4

Substituting these values in eqn (i), we get

⇒ \(P_f =(2)\left(\frac{1200}{300}\right)^{\frac{1.4}{1.4-1}}=(2)(4)^{1.4 / 0.4}\)

= \(2\left(2^2\right)^{7 / 2}=(2)(2)^7=2^8=256 \mathrm{~atm}\)

Question 30. If AU and AW represent the increase in internal energy and work done by the system respectively in a thermodynamical process, which of the following is true?

1. ΔU = – ΔW, in adiabatic process
2. ΔU= ΔW, in an isothermal process
3. ΔU = ΔW, in a adiabatic process
4. ΔU = -ΔW, in an isothermal process

Answer: 1. ΔU = – ΔW, in adiabatic process

From the first law of thermodynamics,

⇒ \(\Delta Q=\Delta U+\Delta W\)

for adiabatic process, \(\Delta \mathrm{Q}\)=0

∴ \(\Delta U=-\Delta W\)

Question 31. In a thermodynamic process which of the following statements is not true?

1. In an adiabatic process, the system is insulated from the surroundings
2. In an isochoric process, pressure remains constant
3. In an isothermal process, the temperature remains constant
4. In an adiabatic process PV₁ = constant

Answer: 2. In an isochoric process pressure remains constant

In an isochoric process, volume remains constant.

Question 32. If Q, E, and W denote respectively the heat added, change in internal energy, and the work done in a closed cycle process, then:

1. W= 0
2. Q=W=0
3. E = 0
4. g = 0

Answer: 3. E = 0

In the cyclic process, since initial and final states are of the same internal energy is a state function therefore initial and final internal energies are also the same. So, the charge in internal energy is the same, hence E = 0

Question 33. Two moles of an ideal gas are taken in a cyclic process abcda. During the process ab and cd temperatures are 500 K and 300 K respectively. Calculate heat absorbed by the system (in 2 = 0.69 and R = 8.3 J/mol-K).

1. 2290.3 J
2. 2209.3 J
3. 2029.3 J
4. 2293.3 J

Answer: 1. 2290.3 J

From the diagram, it is clear that:

⇒ \(Q_{a b c d a}=Q_{a b}+Q_{b c}+Q_{c d}+Q_{d a}\)

Here a b, b c, c d, and d a represent isothermal expansion, isochoric compression, isothermal compression, and isochoric expansion respectively,

⇒ \(Q_{b c} =Q_{d a}\)

⇒ \(Q_{a b c d a} =Q_{a b}+Q_{c d}\)

⇒ \(Q_{a b c d a} =Q_{a b}+Q_{c d}\)

= \(\eta R T_1 \log \left[\frac{2 V_0}{V_0}\right]+\mu R T_2 \log \left[\frac{V_0}{2 V_0}\right]\)

= \(2 \times 8.3 \times 0.09(500-300)\)

= 2290.3 J

Question 34. A sample of gas expands from volume V₁ to V₂. The amount of work done by the gas is greatest when the expansion is:

1. adiabatic
2. isobaric
3. isothermal
4. equal in all the above cases

Answer: 2. isobaric

The P-V diagram for the isobaric, isothermal, and adiabatic processes of an ideal gas is shown in the graph below,

In thermodynamics, for some volume change, the work done is maximum for the curve having maximum area enclosed with the volume axis.

The area enclosed by the curve,

⇒ (Slope of curve ) alpha

⇒ \((\text { slope })_{\text {isobaric }}<(\text { slope })_{\text {isothermal }}<(\text { slope })_{\text {adiabatic }}\)

⇒ \((\text { Area })_{\text {isobaric }}>(\text { Area })_{\text {isothermal }}>(\text { Area })_{\text {adiabatic }}\)

Hence, the work done is maximum in the isobaric process.

⇒ \((\text { Slope })_{\text {adiabatic }} =-\gamma\left(\frac{P}{V}\right)\)

⇒ \(\text { and }(\text { Slope })_{\text {isothermal }} =-\frac{P}{V} \)

⇒ \((\text { Slope })_{\text {adiabatic }} =\gamma \times(\text { slope })_{\text {isothermal }}\)

The slope of the adiabatic curve is always steeper than that of the isothermal curve

Question 35. An ideal gas A and a real gas B have their volumes increased from V to 2V under isothermal conditions. The increase in internal energy:

1. will be the same in both A and B
2. will be zero in both the gases
3. of B will be more than that of A
4. of A will be more than that of B

Answer: 2. will be zero in both the gases

An isothermal change occurs when the pressure and volume of a gas change without the temperature changing. There is a free exchange of heat between the gas and its surroundings during such a transition.

T= constant, \(\Delta\)= 0

∴ So, internal energy (U) remains constant.

Question 36. A thermodynamic system is taken from state A to B along ACB and is brought back to A along BDA as shown in the diagram. The net work done during the complete cycle is given by the area:

1. \(p_1 A C B p_2 p_1\)
2. \(A C B B^{\prime} A^{\prime} A\)
3. A C B D A
4. \(A D B B^{\prime} A^{\prime} A\)

Answer: 3. A C B D A

Work done during path ACB = area ACBB’ A’ A

Work done during going from ACB and then to BDA path is = area ACB B’A’A – area BDAA’ B’ B

= area ACBDA

Question 37. A thermodynamic process is shown in the figure. The pressure and volumes corresponding to some points in the figure are:

⇒ \(P_A=3 \times 10^4 \mathrm{~Pa} ; V_A=2 \times 10^{-3} \mathrm{~m}^3 \)

⇒ \(P_B=8 \times 10^4 \mathrm{~Pa} ; V_D=5 \times 10^{-3} \mathrm{~m}^3\)

In the process, AB, 600 J of heat is added to the system. The change in internal energy of the system is process AC would be

1. 560 J
2. 800 J
3. 600 J
4. 640 J

Answer: 1. 560 J

Since AB is an isochoric process. So no work is done. \mathrm{BC} is isobaric process

⇒ \(\mathrm{W}=\mathrm{P}_{\mathrm{B}} \times\left(\mathrm{V}_{\mathrm{D}}-\mathrm{V}_{\mathrm{A}}\right)=240 \mathrm{~J}\)

⇒ \(\Delta \mathrm{Q}=600+200=800 \mathrm{~J}\)

Using \(\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}\)

∴ \(\Delta \mathrm{U}=\Delta \mathrm{Q}-\Delta \mathrm{W}=800-240=560 \mathrm{~J}\)

Question 38. The efficiency of an ideal heat engine working between the freezing point and boiling point of water is :

1. 6.25%
2. 20%
3. 26.8%
4. 12.5%

Answer: 3. 26.8%

We know that the efficiency of an ideal heat engine \(\eta=\left(1-\frac{T_2}{T_1}\right)\)

Where, \(T_1=100+273=373 \mathrm{~K}\)

⇒ \(T_2=0.273=273 \mathrm{~K}\)

Putting the value of \(T_1 and T_2\) in eq. (1), We get,

⇒ \(\eta =1-\frac{273}{373}=\frac{373-273}{373}=\frac{100}{373}\)

=0.268

Now, % \(\eta\) =0.268 x 100=26.8 %

Question 39. A heat engine has a source at a temperature of 527°C and a sink at a temperature of 127°C. If the useful work is required to be done by the engine at the rate of 800 W, then find the amount of heat absorbed by the sink per second from the source in calories. Also, find the efficiency of the heat engine.

1. \(381 \mathrm{cal} \mathrm{s}^{-1}, 50 \%\)
2. \(318 \mathrm{cal} \mathrm{s}^{-1}, 50 \%\)
3. \(381 \mathrm{cal} \mathrm{s}^{-1}, 45 \%\)
4. \(318 \mathrm{cal} \mathrm{s}^{-1}, 45 \%\)

Answer: 1. \(381 \mathrm{cal} \mathrm{s}^{-1}, 50 \%\)

Given

A heat engine has a source at a temperature of 527°C and a sink at a temperature of 127°C. If the useful work is required to be done by the engine at the rate of 800 W, then find the amount of heat absorbed by the sink per second from the source in calories.

From question, \(T_1=800 \mathrm{~K}, T_2=400 \mathrm{~K}\) and \(W=a_1-a_2=800 \mathrm{~W}\)

Work done per unit amount of heat absorbed is:

⇒ \(\frac{W}{Q_1} =\frac{T_2-T_2}{T_1}=\frac{800-900}{800}=\frac{1}{2}\)

⇒ \(\frac{800}{Q_1} =\frac{1}{2}\)

⇒ \(Q_1=1600 \mathrm{~W}\)

⇒ \(Q_1=\frac{1600}{4.2}=381 \mathrm{cal} \mathrm{s}^{-1}\)

∴ Efficiency, \(\eta=\frac{T_1-T_2}{T_1}=\frac{800-400}{800}=\frac{1}{2}\)= 50%

Question 40. The temperatures of the source and sink of a heat engine are 127°C and 27°C respectively. An inventor claims its efficiency to be 26%, then:

1. it is impossible
2. it is possible with a high probability
3. it is possible with a low probability
4. Data is insufficient

Answer: 1. it is impossible

Efficiency of heat engine is, \(\eta =1-\frac{T_2}{T_1}\) { or } \(\eta=\frac{T_1-T_2}{T_1}\)

⇒ T₁ = temperature of sink

⇒  T₂=Temperature of source

Given, T₁=273+127=400 K

⇒ T₂=273+27=300 K

⇒ \(\eta =\frac{400-300}{400}=\frac{100}{400}\)

=0.25 = 25 %

Hence, 26% efficiency is impossible for a given heat engine

Question 41. A refrigerator works between 4°C and 30°C. It is required to remove 600 calories of heat every second to keep the temperature of the refrigerated space constant. The power required is (Take, 1 cal = 4.2 Joules):

1. 23.65 W
2. 236.5 W
3. 2365 W
4. 2.365 W

Answer: 2. 236.5 W

According to the question, Temperature of source, \(T_1=30^{\circ} \mathrm{C}=30+273\)

⇒ \(T_1=303 \mathrm{~K}\)

Temperature of sink, \(T_2=4^{\circ} \mathrm{C}=4+273\)

⇒ \(T_2=277 \mathrm{~K}\)

We know that \(\frac{Q_1}{Q_2} =\frac{T_1}{T_2}\)

⇒ \(\frac{Q_2+W}{Q_2} =\frac{T_1}{T_2}\left\{ W=\mathrm{Q}_1-\mathrm{Q}_2\right\}\)

⇒ \(W T_2+T_2 Q_2 =T_1 Q_2 \)

⇒ \(W T_2 =T_1 Q_2-T_2 Q=Q_2\left(T_1-T_2\right)\)

W =\(\frac{Q_2}{T_2}\left(T_1-T_2\right)=Q_2\left(\frac{T_1}{T_2}-1\right)\)

=600 \(\times 4.2\left(\frac{303}{277}-1\right)\)

=600 \(\times 4.2 \times \frac{26}{277} \)

=236.5 \(\mathrm{~J}=\text { Retain }\)

Power =\(\frac{\text { Work done }}{\text { time }}\)

= \(\frac{236.5}{1}=236.5 \mathrm{~W}\)

Question 42. The temperature inside a refrigerator is t₂°C and the room temperature is t₁°C. The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be:

1. \(\frac{t_1}{t_1-t_2}\)
2. \(\frac{t_1+273}{t_1-t_2}\)
3. \(\frac{t_2+273}{t_1-t_2}\)
4. \(\frac{t_1+t_2}{t_1+273}\)

Answer: 2. \(\frac{t_1+273}{t_1-t_2}\)

If \(Q_1\)= amount of heat delivered to the room

W = electrical energy consumed

⇒ \(T_1 \)= room temperature =\(t_1+273 \)

⇒ \(T_2 \)= temp. of sink =\(t_2+273\)

Then, for the refrigerator,

⇒ \(\frac{Q_1}{W} =\frac{Q_1}{Q_1-Q_2}=\frac{T_1}{T_1-T_2}\)

⇒ \(\frac{Q_1}{1} =\frac{t_1+273}{\left(t_1+273\right)-\left(t_2+273\right)}\)

∴ \(Q_1 =\frac{t_1+273}{\left(t_1-t_2\right)}\)

Question 43. The coefficient of performance of a refrigerator is 5. If the temperature inside the freezer is – 20°C, the temperature of the surroundings to which it rejects heat is:

1. 31°C
2. 41°C
3. 11°C
4. 21°C

Answer: 1. 31°C

Coefficient of performance of the refrigerator

C.O.P =\(\frac{T_L}{T_H-T_L}\)

Where\( T_L\)= Lower temperature

⇒ \(T_H\)= Higher temperature

5 =\(\frac{T_L}{T_H-T_L}\)

⇒  \(T_H =\frac{6}{5} T_L\)

= \(\frac{6}{5} \times 253=303.6 \mathrm{~K}\)

= 31 \(\dot{\mathrm{C}}\)

Question 44. Which of the following processes is reversible?

1. Transfer of heat by conduction.
2. Transfer of heat by radiation.
3. Isothermal compression.
4. Electrical heating of a nichrome wire.

Answer: 3. Isothermal compression.

Isothermal compression is reversible. for example; Carnot cycle, heat engine.

Question 45. The efficiency of a Carnot engine depends upon:

1. the temperature of the sink only
2. the temperature of the source and sink
3. the volume of the cylinder of the engine
4. the temperature of the source only.

Answer: 2. the temperature of the source and sink

The efficiency of a camot engine is given by :\(\eta=1-\frac{T_2}{T_1}\)

Where, \(T_1\) = Temperature of source

⇒ \(T_2=\)= temperature of sink

This confirms that the efficiency of the Carnot engine depends upon the temperature of the source and also the temperature of the sink

Question 46. A Carnot engine having the efficiency of a heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at a lower temperature is:

1. 1 J
2. 90 J
3. 99 J
4. 100 J

Answer: 2. 90 J

In case of carnot engine, efficiency =\(\frac{\text { Work }}{\text { heat absorbed }}\)=\(\frac{W}{q_1}\)

⇒ \(\frac{W}{q_1} =\frac{1}{10}\)

⇒ \(\frac{10 \mathrm{~J}}{q_1} =\frac{1}{10}\)

⇒ \(q_1 =100 \mathrm{~J}\)

When the engine is reversed then\( W+q_2 =q_1 \)

⇒ \(10+q_2 \)=100

∴ \(q_2 =90 \mathrm{~J}\)

Question 47. Two Carnot engines A and B are operated in series. Engine A receives heat from the source at temperature T₁ and rejects the heat to the sink at temperature T. The second engine B receives the heat at temperature T and rejects to its sink at temperature T₂. For what value of T the efficiencies of the two engines are equal:

1. \(\frac{T_2-T_2}{2}\)
2. \(T_1 T_2\)
3. \(\sqrt{T_1 T_2}\)
4. \(\frac{T_1+T_2}{2}\)

Answer: 3. \(\sqrt{T_1 T_2}\)

Given

Two Carnot engines A and B are operated in series. Engine A receives heat from the source at temperature T₁ and rejects the heat to the sink at temperature T. The second engine B receives the heat at temperature T and rejects to its sink at temperature T₂.

We know that the efficiency of the Carnot engine,

⇒ \(\eta=1-\frac{T_2}{T_1}\)

Where, \(T_1\)= temperature of source

⇒ \(T_2\)= temp of sink

For engine A, \(\eta_{\mathrm{A}}=1-\frac{T}{T_1}\)

engine B, \(\eta_{\mathrm{B}}=1-\frac{T_2}{T}\)

From question, \(\eta_A =\eta_B\)

⇒ \(1-\frac{T}{T_1} =1-\frac{T_2}{T}\)

⇒ \(\frac{T}{T_1}=\frac{T_2}{T} =T^2\)

⇒ \(T^2 =T_1 T_2 \)

T =\(\sqrt{T_1 T_2}\)

Question 48. An engine has an efficiency of 1/6. When the temperature of the sink is reduced by 62°C, its efficiency is doubled. Temperatures of the source are:

1. 37°C
2. 62°C
3. 99°C
4. 124°C

Answer: 3. 99°C

Using the formula for efficiency, \(\eta =1-\frac{T_2}{T_1} \)

⇒ \(\frac{1}{6} =1-\frac{T_2}{T_1}\)

⇒ \(\frac{T_2}{T_1} =\frac{5}{6}\)

Since the temp. of the source remains unchanged,

⇒ \(2 \times \frac{1}{6} =1-\frac{T_2-60}{T_1}\)

⇒ \(\frac{1}{3} =1-\frac{\left(T_2-62\right)}{T_1}\)

⇒ \(\frac{2}{3} =\left[\frac{5}{2}-2\right] T_1 \)

⇒ \(T_1 =3 T_2-186\)

⇒ \({\left[\frac{5}{2}-2\right] T_1}\) =186

∴ \(T_1 =372 \mathrm{~K}=99^{\circ} \mathrm{C}\)

Question 49. A Carnot engine whose sink is at 300 K has an efficiency of 40%. By how much should the temperature of the source be increased to increase its efficiency by 50% of the original efficiency?

1. 380 K
2. 275 K
3. 325 K
4. 250 K

Answer: 4. 250 K

Efficiency of Carnot engine,

⇒ \(\eta =1-\frac{T_2}{T_1}\)

⇒ \(\frac{T_2}{T_1} =1-\eta\)

⇒ \(\frac{300}{T_1} =1-\frac{40}{100}=\frac{3}{5}\)

⇒ \(\mathrm{~T}_1 =500 \mathrm{~K}\) or

New efficiency, \(\eta^{\prime}=\eta+\frac{50}{100} \eta=\frac{3}{2} \eta=60 \%\)

⇒ \(\frac{T_2}{T_1}=1-\frac{60}{100}=\frac{2}{5} \)

⇒ \(T_1^{\prime}=\frac{5}{2} \times T_2=\frac{5}{2} \times 300=750 \mathrm{~K}\)

Increase in temperature of the source,

⇒ \(\Delta \mathrm{T}=T_1^{\prime}-T_1 \)

∴ \(\Delta \mathrm{T}=750-500=250 \mathrm{~K}\) .

Question 50. An ideal gas heat engine operates in a Carnot cycle between 227°C and 127°C. It absorbs 6 x 10⁴ cal of heat at higher temperatures. The amount of heat converted into work is:

1. 4.8 x 10⁴cals
2. 6 x 10⁴cals
3. 2.4 x 10⁴cals
4. 1.2 x 10⁴cals

Answer: 4. 1.2 x 10⁴cals

For a Carnot engine efficiency, \(\eta =1-\frac{T_2}{T_1}\)

= \(1-\frac{127+273}{227+273}\)

= \(1-\frac{400}{500}=\frac{1}{5}\)

Now, \( \eta =\frac{\text { Work Output }}{\text { Heat Output }}\)

= \(\frac{\mathrm{W}}{6 \times 10^4}\)

∴ \(\mathrm{~W} =\eta \times 6 \times 10^4 \)

= \(\frac{1}{5} \times 6 \times 10^4\)

= \(1.2 \times 10^4 \mathrm{cal}\).

Question 51. The efficiency of the Camot engine is 50% and the temperature of the sink is 500 K. If the temperature of the source is kept constant and its efficiency raised to 60%, then the required temperature of the sink will be:

1. 100 K
2. 600 K
3. 400 K
4. 500 K

Answer : 3. 400 K

⇒ \(\% \eta=\left(1-\frac{T_2}{T_1}\right) \times 100\)

For 50 \(\%, \frac{50}{100}=1-\frac{50}{11}\)

⇒ \(T_1=1000 \mathrm{~K}\)

aim for 60 \(\%, \frac{60}{100}=1-\frac{T_2}{1000}\)

∴ \(T_2=400 \mathrm{~K}\)

Question 52. The (W/Q) of a Camot engine is 1/6, now the temperature of the sink is reduced by 62°C, then this ratio becomes twice, therefore the initial temperature of the sink and source are respectively:

1. 33°C, 67°C
2. 37°C, 99°C
3. 67°C, 33°C
4. 97 K, 37 K

Answer: 2. 37°C, 99°C

⇒ \(\frac{1}{6}=-\frac{T_2}{T_1}{ or }\frac{5}{6}=\frac{T_2}{T_1}\)

Now,\(\frac{1}{3}=1-\frac{T_2-62}{T_1}=1-\frac{5}{6}+\frac{62}{T_1}\)

⇒ \(\mathrm{~T}_1=62 \times 6=372 \mathrm{~K}=99^{\circ} \mathrm{C}\)

and \(\mathrm{T}_2=310 \mathrm{~K}=37^{\circ} \mathrm{C}\)

Question 53. The efficiency of a Carnot engine operating between temperatures of 100°C and-23°C will be

1. \(\frac{100-23}{273}\)
2. \(\frac{100+23}{373}\)
3. \(\frac{100+23}{100}\)
4. \(\frac{100-23}{100}\)

Answer: 2. \(\frac{100+23}{373}\)

The efficiency of the Carnot engine is given by, \(\eta=1-\frac{T_2}{T_1}=\frac{T_1-T_2}{T_1}\)

Given, \(T_1\) = temperature of reservoir

= \(100+273=273 \mathrm{~K}\)

⇒ \(T_2\) = temperature of sink

=\(-23+273=250 \mathrm{~K}\)

Substituting in Eq. (1), we get,

=\(\frac{100+23}{373}=\frac{123}{373}\)

NEET Physics For Thermal Properties Of Matter Multiple Choice Questions

Question 1. Mercury thermometer can be used to measure temperature up to:

1. 260°C
2. 100°C
3. 360°C
4. 500°C

Answer: 1. 260°C

A mercury thermometer is a liquid thermometer that uses the homogeneous variation in volume of a liquid as a temperature. Mercury is opaque and bright, making it easy to see in the glass tube, and it is a good heat conductor, soon reaching the temperature of the hot bath. A mercury thermometer can be used to measure temperatures up to 300°C or so because mercury begins to evaporate at 367°C.

Question 2. A Centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°. What is the fall in temperature as registered by the Centigrade thermometer?

1. 80°
2. 60°
3. 40°
4. 30°

Answer: 3. 40°

Given

A Centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°.

The relation between the Celsius scale and the Fahrenheit scale is \(\frac{C}{100}=\frac{F-32}{180}\)

Putting value of F=\(140^{\circ}\), we get

⇒ \(\frac{C}{100}=\frac{140-32}{180}\)=0.6

C = 60°

Hence, Fall in temperature = Temperature of boiling water – final temperature

100°C – 60°C = 40°C

Question 3. A copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in length independent of increase in temperature. The length of aluminium rod is:  \(\alpha_{\mathrm{Cu}}=1.7\times10^{-5}\mathrm{~K}^{-1},\alpha_{\mathrm{Al}}=2.2 \times 10^{-5} \mathrm{~K}^{-1}\)

1. 113.9 cm
2. 88 cm
3. 68 cm
4. 6.8 cm

Answer: 3. 68 cm

Given

A copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in length independent of increase in temperature.

According to the question,

⇒ \(L_w=l_w\left(1+\alpha_w \Delta T\right)\)    →  Equation 1

⇒ \(L_{\mathrm{cu}}=l_{\mathrm{cu}}\left(l+\alpha_{\mathrm{cu}} \Delta t\right)\)  →  Equation 2

⇒ \(L_{\mathrm{A} l}=l_{\mathrm{A} l}\left(A+\alpha_{\mathrm{A} l} \Delta T\right)\)    →  Equation 3

From equation. (1) and equation (3),

Read and Learn More NEET Physics MCQs

⇒ \(L_{\mathrm{A} l}-L_{\mathrm{C} u}=L_{\mathrm{A} l}-L_{\mathrm{C} u}+\left(l_{\mathrm{A} l} \alpha_{\mathrm{A} l}-l_{\mathrm{C} u} \alpha_{\mathrm{Cu}}\right) \Delta T\)

Since, \(l_{\mathrm{A} l} \alpha_{\mathrm{A} l}=l_{\mathrm{C} u} \alpha_{C u}\)

⇒ \(l_{\mathrm{A} l}=\frac{l_{C u} \alpha_{\mathrm{Cu}}}{\alpha_{\mathrm{A} l}}\)

= \(\frac{8.8 \times 1.7 \times 10^{-5}}{2.2 \times 10^{-5}}=68 \mathrm{~cm}\)

∴ \(l_{\mathrm{Al}}=68 \mathrm{~cm}\)

Question 4. Coefficient of linear expansion of brass and steel rods and \(\alpha_I \text { and } \alpha_2\). Length of brass and steel rods are \(\mathrm{l}_1\text { and } I_2\) respectively. If I₁-I₂ is maintained the same at all temperatures, which one of the following relations holds good?

1. \(\alpha_1 l_2^2=\alpha_1{ }^2 l_2^2\)
2. \(\alpha_1{ }^2 l_2=\alpha_2^2 l_1\)
3. \(\alpha_1 l_1=\alpha_2 l_2\)
4. \(\alpha_1 l_2=\alpha_2 l_1\)

Answer: 3. \(\alpha_1 l_1=\alpha_2 l_2\)

Given

Coefficient of linear expansion of brass and steel rods and \(\alpha_I \text { and } \alpha_2\). Length of brass and steel rods are \(\mathrm{l}_1\text { and } I_2\) respectively. If I₁-I₂ is maintained the same at all temperatures

The change in length for both rods should be the same,

⇒ \(\Delta l_1 =\Delta l_2\)

⇒ \(l_1 \alpha_1 \Delta T =l_2 \alpha_2 \Delta T\)

∴ \(l_1 \alpha_1 =l_2 \alpha_2\)

Question 5. The value of the coefficient of volume expansion of glycerin is \(5 \times 10^{-4} \mathrm{~K}^{-1}\). The fractional change in the density of glycerin for a rise of 40°C in its temperature is:

1. 0.015
2. 0.020
3. 0.025
4. 0.010

Answer: 2. 0.020

The value of coefficient of volume expansion of glycerin is =\(5 \times 10^{-4} \mathrm{~K}^{-1}\)

We know that, \(d_f=\frac{d_i}{(1+V \Delta \mathrm{T})}\)

Fractional change =\(\frac{d_i-d_f}{d_f}=1-\frac{d_f}{d_i}\)

= \(1-(1+V \Delta T)^{-1}=1-(1-V \Delta T)\)

⇒ \(\left\{\mathrm{Q}(1+x)^n \approx 1+n x\right\}\)

= V \(\Delta T=5 \times 10^{-4} \times 40\)=0.020

Question 6. The density of water at 20°C is 998 kg/m³ and at 40°C 992 kg/m³. The coefficient of volume expansion of water is:

1. 3 x 10^-4/°C
2. 2 x 10^-4/°C
3. 6 x 10^-4/°C
4. 10^-3/°C

Answer: 1. 3 x 10-4/°C

According to the question,

⇒ \(T_1=20^{\circ} \mathrm{C}, T_2=40^{\circ} \mathrm{C}\)

⇒ \(\rho_{20}=998 \mathrm{~kg} / \mathrm{m}^3 \rho_{40}=992 \mathrm{~kg} / \mathrm{m}^3\)

So, \(\rho_{\mathrm{T}_2}=\frac{\rho_{\mathrm{T}_1}}{(1+v \Delta T)}=\frac{\rho_{\mathrm{T}_1}}{1+v\left(T_2-T_1\right)}\)

Putting the values we get, 992=\(\frac{998}{1+\gamma(40-20)}\)

992=\(\frac{998}{1+20 \gamma}\)

⇒ \(992(1+20 \gamma)\) =998

1+20\( \gamma =\frac{998}{992} \)

⇒ \(20 \gamma =\frac{6}{992} \)

=\(\frac{6}{992} \times \frac{1}{20} =3 \times 10^{-1 \circ} \mathrm{C}\)

Question 7. (A)The weight of the sphere in the air is 50 g. Its weight is 40 g in a liquid, at a temperature of 20°C. When the temperature increases to 70°C, its weight becomes 45 g. Find: (1) the ratio of densities of liquid at given two temperatures is. (2) the coefficient of cubical expansion of liquid assuming that there is no expansion of the volume of a sphere.

Answer: 3.

Given

The weight of the sphere in the air is 50 g. Its weight is 40 g in a liquid, at a temperature of 20°C. When the temperature increases to 70°C, its weight becomes 45 g.

(1) \(W_{\text {apparent }}=W_{\text {air }}-\rho V g\)

Let \(\rho_1=\text { density of liquid at } 20^{\circ} \mathrm{C}\)

40= \(50-V \rho_1 g \)

10= \(V \rho_1 g\)

Again, Let,\(\rho_2\)=density of liquid at  \(70^{\circ} \mathrm{C}\)

45= \(50-V \rho_2 g \)

5= \(V \rho_2 g \)

From eq. (1) and (2)

∴ \(\frac{\rho_1}{\rho_2}=\frac{2}{1}\)

(2)  Because \(\rho_2=\frac{M}{V_1(1+\gamma \Delta \theta)}=\frac{\rho_1}{(1+\gamma \Delta \theta)}\)

⇒ \(\frac{\rho_1}{\rho_2}=1+\gamma \Delta \theta\)

Since, \(\frac{\rho_1}{\rho_2}=2 \)

⇒ \(2=1+\gamma \Delta \theta \)

⇒ \(\gamma \Delta \theta=1\)

⇒ \(\gamma=\frac{1}{\Delta \theta}\)

∴ \(\gamma=\frac{1}{70-20}=\frac{1}{50}\)=0.02

Question 8. The quantities of heat required to raise the temperature of two solid copper spheres of radii \(r_1 \)  and \(r_2\left(r_1=1.5 r_2\right)\) through 1 K are in the ratio of:

1. \(\frac{9}{4}\)
2. \(\frac{3}{2}\)
3. \(\frac{5}{3}\)
4. \(\frac{27}{8}\)

Answer: 4. \(\frac{27}{8}\)

Heat required

Q = \(m c \Delta \mathrm{T}\)

= \(\left(\frac{4}{3} \pi r^3 \cdot \rho\right) c \Delta \mathrm{T}\)

Since \(\pi, \rho, c, \Delta\) t are constant.

⇒ \(\mathrm{Q} \propto r^3 \).

or, \(\frac{\mathrm{Q}_1}{\mathrm{Q}_2} =\frac{r_1^3}{r_2{ }^3}=\left(\frac{r_1}{r_2}\right)^3=\left(\frac{1.5 r_2}{r_2}\right)^3 \)

=\(\frac{27}{8}\)

Question 9. The thermal capacity of 40 g of aluminium (s-0.2 cal/g-K) is:

1. 168 J/K
2. 672 J/K
3. 840 J/K
4. 33.6 J/K

Answer: 4. 33.6 J/K

The thermal capacity of a body is defined as the amount of heat required to raise the temperature of the (whole) body through 1°C or 1 K.

The amount of heat energy required (ΔQ) to raise the temperature of mass m of a body through temperature range (ΔT) is, ΔQ = ms (ΔT)

where, s is the specific heat of the body, when ΔT = 1K,

ΔQ = thermal capacity

Thermal capacity = s x m x 1 = ms

Here,m = 40 g, s = 0.2 cal/g K

Thermal capacity = 40 x 0.2 = 8 cal/K

= 4.2 x 8 J/K = 33.6 J/K

Question 10. Steam at 100°C is passed into 20 g of water at 10°C. When water acquires a temperature of 80°C, the mass of water present will be [Take specific heat of water = 1 cal g^-1 C^-1latent heat of steam = 540 cal g^-1]:

1. 24 g
2. 31.5 g
3. 42.5 g
4. 22.5 g

Answer: 4. 22.5 g

Heat gain by water = heal loss of steam

20 x 1 x (80 – 10) = m x 540 + m x 1 x (100 – 80) 1400 = 560 m

m = 2.5 g

Total mass of water = 20 + 2.5 = 22.5 g

Question 11. A piece of ice falls from a height h so that it melts completely. Only one quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall. The value of h is [Latent heat of ice is 3.4 x 10⁵ J/kg andg= 10 N/kg]:

1. 544 km
2. 136 km
3. 38 km
4. 34 km

Answer: 2. 136 km

Given that:

A piece of ice falls from a height h so that it melts completely. Only one quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall.

mgH = ml

H = \(\frac{4 L}{g}=\frac{4 \times 3.4 \times 10^5}{10}\)

=136 km

Question 12. If 1 g of steam is mixed with 1 g of ice, then the resultant temperature of the mixture is:

1. 270°C
2. 230°C
3. 100°C
4. 50°C

Answer: 3. 100°C

The heat required by 1 g of ice at 0°C to melt into 1g of water at 0°c,

⇒ \(Q_1 \)=m L (L =latent heat of fusion )

=\(1 \times 80=80 \mathrm{cal}(L=80 \mathrm{cal} / \mathrm{g})\)

Heat required by 1 g of water at 0°C to boil at 100°C,

⇒ \(Q_2 =m c \Delta \mathrm{T}\) (c = specific heat of water) =

= 1 x 1(100-0)

⇒ \((c \left.=1 \mathrm{cal} / \mathrm{g}^{\circ} \mathrm{C}\right)\)

=100 cal

Thus, the total heat required by 1 g of ice to reach a temperature of 100°C,

⇒ \(Q=Q_1+Q_2=80+100=180 \mathrm{cal}\)

Heat available with 1 g of steam to condense into 1 g of water at 100°C,

⇒ \(Q^{\prime}= m L^{\prime}\)

⇒ \(\left(L^{\prime}\)= latent heat of vaporisation

= 1 x 536 cal ( L’ =536 call/g)

= 536 cal

The whole steam will not be condensed and ice will attain a temperature of 100°C. Thus, the temperature of the mixture is 100°C.

Question 13. The energy that will be ideally radiated by a 100kw transmitter in 1 hour is:

1. 36 x 10⁷J
2. 36 x 10⁴J
3. 36 x 10³J
4. 36 x 10⁵J

Answer: 1. 36 x 10⁷J

Power, \(\mathrm{P}=100 \mathrm{kw}=100 \times 10^3 \mathrm{~W}\) ;

Time, t = 1 hour =\(3600 \mathrm{~s}\)

Energy, \(\mathrm{E}=\mathrm{P} \times \mathrm{t} =100 \times 10^3 \times 3600\)

= \(36 \times 10^7 \mathrm{~J}\)

Question 14. A deep rectangular pond of surface area A, containing water (density = p specific heat capacity = 5), is located in a region where the outside air temperature is steady value at – 26°C. The thickness of the ice layer in the pond, at a certain instant x. Taking the thermal conductivity of ice as K, and its specific latent heat of fusion is L, 1 the rate of increase of the thickness of the ice layer, at this instant would be given by:

1. \(\frac{26 K}{\rho \mathrm{x}(L-4 s)}\)
2. \(\frac{26 K}{\left(\rho x^2 L\right)}\)
3. \(\frac{26 K}{(\rho x L)}\)
4. \(\frac{26 K}{\rho \mathrm{x}(L+4 s)}\)

Answer: 3. \(\frac{26 K}{(\rho x L)}\)

Given

A deep rectangular pond of surface area A, containing water (density = p specific heat capacity = 5), is located in a region where the outside air temperature is steady value at – 26°C. The thickness of the ice layer in the pond, at a certain instant x. Taking the thermal conductivity of ice as K, and its specific latent heat of fusion is L,

If the area of the cross-section of a surface is not uniform or if the steady state condition is not reached the heat flow equation can be applied to a thin layer of material perpendicular to the direction of heat flow.

The rate of heat flow by conduction for the growth of ice is given by,\(\frac{d \theta}{d t}=\frac{K A\left(\theta_0-\theta_1\right)}{x}\)    → Equation 1

where,\(\mathrm{d} \theta=\rho \mathrm{A} d x L, \theta_0=0 \text { and } \theta_1=-\theta \)

⇒ \(\theta_0=0^{\circ} \mathrm{C} \Rightarrow \theta_1=-26^{\circ} \mathrm{C}\) .

Given that the rate of increase in thickness can be calculated from the equation. (1),

⇒ \(\frac{d \theta}{d t} =\frac{K A\left(\theta_0-\theta_1\right)}{x}\)

⇒ \(\frac{\rho A d x L}{d t} =\frac{K A\left(\theta_0-\theta_1\right)}{x}\)

⇒ \(\frac{d x}{d t} =\frac{K A\left(\theta_0-\theta_1\right)}{\rho A x L}\)

∴ \(\frac{K[0-(-26)]}{\rho x L} =\frac{26 K}{\rho x L}\)

Question 15. Two rods A and B of different materials are welded together as shown in the figure. Their thermal conductivities are K₁ and K₂. The thermal conductivity of the composite rod will be:

1. \(\frac{K_1+K_2}{2}\)
2. \(\frac{3\left(K_1+K_2\right)}{2}\)
3. \(K_1+K_2\)
4. \(2\left(K_1+K_2\right)\)

Answer: 1. \(\frac{K_1+K_2}{2}\)

Heat flow rate, \(H=H_1+H_2\)

H =\(\frac{K_1 A\left(T_1-T_2\right)}{d}+\frac{K_2 A\left(T_1-T_2\right)}{d}\)

⇒ \(\frac{K_{e g}\left(T_1-T_2\right)}{d} =\frac{A\left(T_1-T_2\right)}{d}\left[K_1+K_2\right]\)

∴ \(K_{\text {eg. }} =\left[\frac{K_1+K_2}{2}\right]\)

Question 16. A spherical black body with a radius of 12 cm radiates 450-watt power at 500 J. If the radius were halved and the temperature doubled, the power radiated in watts would be:

1. 225
2. 450
3. 1000
4. 1800

Answer: 4. 1800

From Stefan’s law, Here radiated power of the black body P=\(\sigma \mathrm{AT}^4\) becomes half then a new area

_⇒ \(A^{\prime}=\frac{A}{4}\)

Power radiation, \(\mathrm{P}^{\prime}=\sigma\left(\frac{A}{4}\right)(2 T)^4\)

Question 17. A black body is at a temperature of 5760 K. The energy of radiation emitted by the body at wavelength 250 nm is U₁, at wavelength 500 nm is U₂ and that at 1000 nm is u₃. Wein’s constant, b = 2.88 x 106 nm. Which of the following is correct?

1. U₃ = 0
2. U₁ > U₂
3. U₂ > U₁
4. U₁ = 0

Answer: 3. U₂ > U₁

Given

A black body is at a temperature of 5760 K. The energy of radiation emitted by the body at wavelength 250 nm is U₁, at wavelength 500 nm is U₂ and that at 1000 nm is u₃. Wein’s constant, b = 2.88 x 106 nm.

Temperature, T_\(1=5760 \mathrm{~K}\) (Given)

Using Wien’s law,

⇒ \(\lambda_m T=b\)  →  Equation 1

b= Wien’s constant =\(2.86 \times 10^6 \mathrm{nmK}\)

From (1) \(\lambda_m=\frac{b}{T}\)

⇒ \(\lambda_m=\frac{2.88 \times 10^6 \mathrm{nmK}}{5760 \mathrm{~K}}=500 \mathrm{~nm}\)

∴ \(U_2>U_1\)

Question 18. Two metal rods 1 and 2 of the same length have the same temperature difference between their ends. Their thermal conductivities are K₁ and K₂ and cross-sectional areas A₁ and A₂ respectively. If the rate of heat conduction in 1 is four times that in 2, then:

1. K₁A₁ = 4K₂A₂
2. K₁A₁ = 2K₂A₂
3. 4K₁A₁ = K₂A₂
4. K₁A₁ =  K₂A₂

Answer: 1. K₁A₁ = 4K₂A₂

Given

Two metal rods 1 and 2 of the same length have the same temperature difference between their ends. Their thermal conductivities are K₁ and K₂ and cross-sectional areas A₁ and A₂ respectively.

Let, L= length of each rod Temperature difference = \(\Delta T\)

The rate of flow of rod (1) is,

⇒ \(H_1=\frac{K_1 A_1 \Delta \mathrm{T}}{L}\)

and Rate of flow of rod (2) is, \(H_2=\frac{K_2 A_2 \Delta T}{L}\)

from the equation,  \(H_1 =4 H_2\)

⇒ \(\frac{K_1 A_1 \Delta \mathrm{T}}{L} =4 \frac{K_2 A_2 \Delta T}{L}\)

∴ \(K_1 A_1 =4 K_2 A_2\)

Question 19. If the radius of a star is R and it acts as a black body, what would be the temperature of the star, in which the rate of energy production is Q?

1. \(\frac{Q}{4 \pi R^2 \sigma}\)
2. \(\left(\frac{Q}{4 \pi R^2 \sigma}\right)^{-\frac{1}{2}}\)
3. \(\left(\frac{4 \pi R^2 Q}{\sigma}\right)^{\frac{1}{4}}\)
4. \(\left(\frac{Q}{4 \pi R^2 \sigma}\right)^{\frac{1}{4}}\)

Answer: 4. \(\left(\frac{Q}{4 \pi R^2 \sigma}\right)^{\frac{1}{4}}\)

From Stefan’s law, we can write,

E=\(\sigma T^4\)

and rate of energy production, Q =\(E \times A \)

= \(\sigma \mathrm{T}^4 A =\sigma T^{4 \pi} 4 \pi \mathrm{R}^2\)

T =\(\left(\frac{Q}{4 \pi \mathrm{R}^2 \sigma}\right)^{1 / 4}\)

Question 20. A slab of stone with an area of 0.36 m2 and thickness of 0.1 m is exposed on the lower surface to steam at 100°. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of the slab is:(Given latent heat of fusion of ice = 3.36 x 105 J kg^-1)

1. 1.24 J/m/s/°C
2. 1.29J/m/s/°C
3. 2.05 J/m/s/°C
4. 1.02J/m/s/°C

Answer: 1. 1.24 J/m/s/°C

Given

A slab of stone with an area of 0.36 m2 and thickness of 0.1 m is exposed on the lower surface to steam at 100°. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted.

We know that,

⇒ \(\frac{d Q}{d t} =\frac{K A}{L}\left(T_1-T_2\right)\)

Q =\(\frac{K A}{L}\left(T_1-T_2\right) t\)

Q = \( m L_f\)

⇒ \(\frac{K A}{L}\left(T_1-T_2\right) t =m L_f\)

K =\(\frac{m \mathrm{~L}_f(\mathrm{~L})}{\mathrm{A}\left(\mathrm{T}_1-\mathrm{T}_2\right) t}\)

= \(\frac{4.8 \times 3.36 \times 10^5 \times 0.1}{0.36 \times 100 \times 3600} \mathrm{~J} / \mathrm{m} / \mathrm{S} /{ }^{\circ} \mathrm{C}\)

= \(\frac{4.8 \times 3.36}{0.36 \times 36}=1.24 \mathrm{~J} / \mathrm{m} / \mathrm{S} /{ }^{\circ} \mathrm{C}\)

Question 21. A cylinder metallic rod is in thermal contact with two reservoirs of heat at its two ends and conducts an amount of heat Q in time t. The metallic rod is melted and the material is formed into a rod of half the radius of the original rod. What is the amount of heat conducted by the new rod when placed in thermal contact with the two reservoirs in time ft?

1. \(\frac{Q}{4}\)
2. \(\frac{Q}{16}\)
3. 2Q
4. \(\frac{Q}{2}\)

Answer: 2. \(\frac{Q}{16}\)

Given

A cylinder metallic rod is in thermal contact with two reservoirs of heat at its two ends and conducts an amount of heat Q in time t. The metallic rod is melted and the material is formed into a rod of half the radius of the original rod.

We know that, Amount of heat, Q=\(\frac{K A\left(\theta_1-\theta_2\right) t}{t}\)

Where, K= coefficient of thermal conduction

⇒ \(\frac{Q}{t} \propto \frac{A}{l} \propto \frac{r^2}{l}\)  →   Equation 1

As the metallic rod is melted and the material is formed into a rod of half the radius,

⇒ \(V_1 =V_2\)

⇒ \(\pi r_1^2 l_1 =\pi r_2^2 l_2 \)

⇒ \(l_1 =\frac{l_2}{4}\)  →  Equation 2

From eq. (1) and eq. (2),

⇒ \(\frac{Q_1}{Q_2}=\frac{r_1^2}{l_2} \times \frac{l_2}{r_2^2}=\frac{r_1^2}{l_2} \times \frac{4 l_1}{\left(r_2 / 2\right)^2}\)

∴ \(Q_1=16 Q_2 \)

Question 22. The total radiant energy per unit area, normal to the direction of incidence, received at a distance R from the centre of a star radius r, whose outer surface radiates as a black body at a temperature T K is given by:

1. \(\frac{\sigma r^2 T^4}{R^2}\)
2. \(\frac{\sigma r^2 T^4}{4 \pi r^2}\)
3. \(\frac{\sigma r^4 T^4}{r^4}\)
4. \(\frac{4 \pi \sigma r^4 T^4}{R^2}\)

Answer: 1. \(\frac{\sigma r^2 T^4}{R^2}\)

Using Stefan’s law A \(\sigma T^4=4 \pi r^2 \sigma T^4\)

∴ \(T_{\mathrm{K}}=\sigma r^2 T^4 / \mathrm{R}^2\)

Question 23. A black body is at 727°C. It emits energy at a rate which is proportional to:

1. (1000)⁴
2. (1000)²
3. (727)⁴
4. (727)²

Answer: 1. (1000)4

According to Stefan’s law,

Rate of radiated energy, \(E \propto T^4\)

where, T= absolute temperature of a black body.

⇒ \(E \propto(727+273)^4\)

or \(E \propto[1000]^4\)

Question 24. Assuming the sun to have a spherical outer surface of radius r, radiating like a black body at temperature fC, the power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is where σ is the Stefan’s constant:

1. \(\frac{r^2 \sigma(t+273)^4}{4 \pi R^2}\)
2. \(\frac{16 \pi^2 r^2 \sigma t^4}{R^2}\)
3. \(\frac{r^2 \sigma(t+273)^4}{R^2}\)
4. \(\frac{4 \pi r^2 \sigma t^4}{R^2}\)

Answer: 3. \(\frac{r^2 \sigma(t+273)^4}{R^2}\)

Solar constant =\(\frac{\sigma\left(4 \pi r^2\right) T^4}{\left(4 \pi R^2\right)}\)

= \(\frac{\sigma r^2(t+273)^4}{R^2}\)

Question 25. A black body at 1227°C emits radiations with maximum intensity at a wavelength of 5000 A. If the temperature of the body is increased by 1000°C, the maximum intensity will be observed at:

1. 3000 A
2. 4000 A
3. 5000 A
4. 6000 A

Answer: 1. 3000 A

By Wein’s displacement law, \(\lambda_m T \)= Constant

we have, \(\frac{\lambda_{m 1}}{\lambda_{m 2}}=\frac{T_2}{T_1}\)

or \(\lambda_{m 2}=\frac{\lambda_{m 1} \times T_1}{T_2}\)

∴ \(\lambda_{m 2}=\frac{5000 \times 1500}{2500}=3000\) .

Question 26. Which of the following rods, (given radius r and length l) each made of the same material and whose ends are maintained at the same temperature will conduct the most heat?

1. r=\(r_0, l=l_0\)
2. r=\(2 r_0, l=l_0\)
3. r=\(r_0, l=2 l_0\)
4. r=\(2 r_0, l=2 l_0\)

Answer: 2. r=\(2 r_0, l=l_0\)

Heat conducted =\(\frac{K A\left(T_1-T_2\right) t}{l}=\frac{K \pi r^2\left(T_1-T_2\right) t}{l}\)

The rod with a maximum ratio of \(\frac{A}{l}\) will conduct the most.

Here the rod r= \( 2 r_0 and l=l_0 \) will conduct most.

Question 27. If km denotes the wavelength at which the radioactive emission from a black body at a temperature TK is maximum, then:

1. \(\lambda_m \propto T^1\)
2. \(\lambda_m\) is independent of T
3. \(\lambda_m \propto T\)
4. \(\lambda_m \propto T^{-1}\)

Ans wer: 4. \(\lambda_m \propto T^{-1}\)

According to Wein’s displacement law

⇒ \(\lambda_m T\)= constant

∴ \(\lambda_m \propto T^{-1}\)

Question 28. Consider a compound slab consisting of two different materials having equal thickness and thermal conductivities K and 2K, respectively. The equivalent thermal conductivity of the slab is:

1. \(\frac{2}{3} K\)
2. \(\sqrt{2} K\)
3. 3 K
4. \(\frac{2}{3} K\)

Answer: 1. \(\frac{2}{3} K\)

The slabs are in series.

Total resistance, \(\mathrm{R}=\mathrm{R}_1+\mathrm{R}_2\)

⇒ \(\frac{l}{K_{e f f}(A)}=\frac{l}{2 K A}+\frac{l}{K A}\)

∴ \(K_{\text {eff }}=\frac{2}{3} K\)

Question 29. The Wein’s displacement law expresses the relation between:

1. wavelength corresponding to maximum energy and temperature.
2. relation energy and wavelength.
3. temperature and wavelength.
4. colour of light and temperature.

Answer: 1. relation energy and wavelength.

According to Wein’s displacement law, the wavelength corresponding to maximum energy is inversely proportional to the absolute temperature of the body \(\lambda_m \propto \frac{1}{T}\)

∴ \(\lambda_m T=\text { constant }\)

Question 30. Which of the following is best close to an ideal black body?

1. Black lamp.
2. Cavity maintained at a constant temperature.
3. Platinum black.
4. A lamp of charcoal heated to high temperature.

Answer: 2. Cavity maintained at a constant temperature.

A perfect black body absorbs all incident radiation without reflecting or transmitting any of it. A black-light absorbs around 96% of incoming radiation.

In reality, a perfect black body may be achieved via a tiny hole in the wall of a uniformly heated hollow body (as indicated in the image). Any radiation that enters the hollow body through the perforations is reflected several times before being absorbed. This can be aided by painting the inside surface with black, absorbing around 96% of the energy at each reflection. The section of the inner surface opposite the hole is conical to prevent the reflected beam from escaping after one reflection.

Question 31. For a black body at a temperature of 727°C, its radiating power is 60 W and the temperature of the surrounding is 227°C. If the temperature of the black body is changed to 1227°C, then its radiating power will be:

1. 304 W
2. 320 W
3. 240 W
4. 120 W

Answer: 2. 320 W

We can use the formula,

⇒ \(P\left(T_4-T_0{ }^4\right)\)

⇒ \(\frac{P_2}{P_1} =\frac{(1500)^4-(500)^4}{(1000)^4-(500)^4}\)

=\(\frac{500^4\left(3^4-1\right)}{500^4\left(2^4-1\right)}\)

⇒ \(\frac{P_2}{60} =\frac{80}{15}\)

∴ \(P_2 =320 \mathrm{~W}\)

Question 32. A cup of coffee cools from 90°C to 80°C in two minutes, when the room temperature is 20°C. The time taken by a similar cup of coffee to cool from 80°C to 60°C at a room temperature same at 20°C is:

1. \(\frac{13}{10} t\)
2. \(\frac{13}{5} t\)
3. \(\frac{10}{13} t\)
4. \(\frac{5}{13} t\)

Answer: 2. \(\frac{13}{5} t\)

Given, Initial temperature \(\left(\mathrm{T}_{\mathrm{i}}\right)=90^{\circ} \mathrm{C}\)

Final temperature \(\left(T_f\right)=80^{\circ} \mathrm{C}\)

Room temperature \(\left(\mathrm{T}_{\mathrm{o}}\right)=20^{\circ} \mathrm{C}\)

Let the time taken be t minutes

According to Newton’s law of cooling,

Rate of cooling,

⇒ \(\frac{d T}{d t} =K\left[\frac{\mathrm{T}_i+\mathrm{T}_f}{2}-\mathrm{T}_o\right]\)

∴ \(\left(\frac{\mathrm{T}_f-\mathrm{T}_i}{t}\right) =K\left[\frac{90+80}{2}-20\right]=K[65]\)

K =\(\frac{10}{65 t}\)  →  Equation 1

In \(2^{\text {nd }}\)condition,

Initial temperature \(\mathrm{T}_{\mathrm{i}}=80^{\circ} \mathrm{C}\)

Final temperature \(\mathrm{T}_{\mathrm{f}}=60^{\circ} \mathrm{C}\)

Let the time taken be t minutes

Then,\(\frac{(80-60)}{t^{\prime}} =\frac{10}{65 t}\left[\frac{(80+60)}{2}-20\right] \frac{20}{t^{\prime}} 10\)

=\(\frac{10}{65 t}(50)\)  →  Equation 2

From equation (1) and (2),

∴ \(\mathrm{t}^{\prime}=\frac{13}{5} t\)

Question 33. An object kept in a large room having an air temperature of 25° C takes 12 minutes to cool from 80° C to 70° C. The time taken to cool the same object from 70° C to 60° C would be nearly :

1. 10 min
2. 12 min
3. 20 min
4. 15 min

Answer: 4. 15 min

From Newton’s law of cooling the expression for the time taken by a body to cool from \(T_1 \text { to } T_2\) when placed in a medium of temperature to is given by :

⇒ \(\frac{T_1-T_2}{t}=\frac{1}{K}\left(\frac{T_1+T_2}{2}-T_0\right)\)

The first condition, When the object cools from \(80^{\circ} \mathrm{C} to 70^{\circ}\) in 12 minutes then from equation 1

⇒ \(\frac{80-70}{12}=\frac{1}{K}\left(\frac{80+70}{2}-25\right)\)

Since, \(T_0\) = 25°C is given

K = 60  →  Equation  2

Again when the object cools from \(70^{\circ} \mathrm{C} to 60^{\circ} \mathrm{C}\) we have

⇒ \(\frac{70-60}{t} =\frac{1}{K}\left(\frac{70+60}{2}-25\right)\)

=\(\frac{10}{t} =\frac{40}{\mathrm{~K}}\)

⇒ \(\frac{10}{t} =\frac{40}{60}\)  From Equation 2

t =15 min

Question 34. A body cools from a temperature of 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton’s law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be:

1. \(\frac{7}{4} T\)
2. \(\frac{3}{2} T\)
3. \(\frac{4}{3} T\)
4. T

Answer: 2. \(\frac{3}{2} T\)

According to the formula from Newton’s law of cooling

In \(\frac{3 T-T}{2 T^{\prime}-T}=K t\)

In(\(2)=K(10)\)

for the next 10 minutes

In \(\frac{2 \mathrm{~T}-\mathrm{T}}{\mathrm{T}^{\prime}-\mathrm{T}} =\mathrm{K}(10)\)

⇒ \(\frac{2 \mathrm{~T}-\mathrm{T}}{\mathrm{T}^{\prime}-\mathrm{T}}\) =2

∴ \(\mathrm{~T}^{\prime} =\frac{3}{2}\)

Question 35. A certain quantity of water cools from 70°C to 60°C in the first 5 min and to 54°C in the next 5 min. The temperature of the surroundings is:

1. 45°C
2. 20°C
3. 42°C
4. 10°C

Answer: 1. 45°C

The question is based on Newton’s law of cooling According to Wien displacement law,

⇒ \(\frac{\theta_1-\theta_2}{\Delta t}=K\left[\frac{\theta_1+\theta_2}{2}-\theta_0\right]\)

Where, \(\theta_0=q\)

⇒ \(\frac{70-60}{5} =K\left[\frac{70+60}{2}-\theta_0\right] \)

=\(K\left[65-\theta_0\right]\)  →  Equation 1

⇒ \(\frac{60-54}{5} =K\left[\frac{60+54}{2}-\theta_0\right]=\mathrm{K}\left[57-\theta_0\right]\) → Equation 2

From (1) and (2),

⇒ \(\frac{2 \times 5}{6} =\left(\frac{65-\theta_0}{57-\theta_0}\right)\)

⇒ \(\frac{5}{3} =\frac{65-\theta_0}{57-\theta_0}\)

2 \(\theta_0 =90 \)

∴ \(\theta_0 =45^{\circ} \mathrm{C}\) .

Question 36. A piece of iron is heated in a flame. If first becomes dull red then becomes reddish yellow and finally turns to white hot. The correct explanation for the above observation is possible by using:

1. Stefan’s law
2. Wein’s displacement law
3. KirchofFs law
4. Newton’s law of cooling

Answer: 2. Wein’s displacement law

We can explain this observation by using \(\lambda_m T=b\)

Which is Wien’s displacement law

Question 37. The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperatures T₁ and T2(T₁ > T₂). The rate of heat transfer, through the rod in a steady state is given by:

1. \(\frac{d \mathrm{Q}}{d t}=\frac{K L\left(T_1-T_2\right)}{A}\)
2. \(\frac{d \mathrm{Q}}{d t}=\frac{K\left(T_1-T_2\right)}{L A}\)
3. \(\frac{d \mathrm{Q}}{d t}=K L A\left(T_1-T_2\right)\)
4. \(\frac{d \mathrm{Q}}{d t}=\frac{K A\left(T_1-T_2\right)}{L}\)

Answer: 4. \(\frac{d \mathrm{Q}}{d t}=\frac{K A\left(T_1-T_2\right)}{L}\)

The rate of heat transfer \((\mathrm{dQ} / \mathrm{dt})\) is given by:

For a rod of length land area of cross-section A whose faces are maintained at temperature T₁ and T₂ respectively then in steady-state the rate of heat flowing from one face to the other in time T is given by Here temperature difference \((\Delta \mathrm{T})=\left(\mathrm{T}_1-\mathrm{T}_2\right)\)

The rate of heat transfer (dQ/dt) is given by

Also, \(\frac{d Q}{d t} =\frac{\Delta T}{R}\)

⇒ \(\mathrm{R} =\frac{L}{k A}\)

∴ \(\frac{d \mathrm{Q}}{d t} =\frac{K A\left(T_1-T_2\right)}{L}\)

NEET Physics For Mechanical Properties Of Solids Multiple Choice Questions

Question 1. The stress-strain curves are drawn for two different materials X and Y. It is observed that the ultimate strength point and the fracture point are close to each other for material X but are far apart for material Y. We can say that materials X and Y are likely to be (respectively):

1. ductile and brittle
2. brittle and ductile
3. brittle and plastic
4. plastic and ductile

Answer: 2. brittle and ductile

Given

The stress-strain curves are drawn for two different materials X and Y. It is observed that the ultimate strength point and the fracture point are close to each other for material X but are far apart for material Y.

As the given factors point and ultimate strength point are close for material X₁ X is brittle and both points are apart for material ϒ Hence Cl is ductile X is brittle and Y is ductile.

Question 2. Given below are two statements: One is labeled as
Assertion and the other is labeled as Reason (R).
Assertion (A): The stretching of a spring is determined by the shear modulus of the material of the spring.
Reason (R): A coil spring of copper has more tensile strength than a steel spring of the same dimensions.
In the light of the above statements, choose the most appropriate answer from the options given below:

1. Both (A) and (R) are true and (R) is not the correct explanation of (A).
2. (A) is true but (R) is false
3. (A) is false but (R) is true
4. Both (A) and (R) are true and (R) is the correct explanation of (A).

Answer: 2. (A) is true but (R) is false

From the concept of Hook’s law, we have,

Normal Stress, (CT) = Ee

where E = Young’s Modulus of Elasticity and e is a strain which gives linear deformation of the object.

Also, Shear Stress, (x) = Gy

where G = Shear Modulus of Elasticity of the material and y is a shear strain which gives angular deformation of the object.

When we stretch a spring, the length of the wire does not change but experiences an angular twist. Hence shear modulus is used to determine the stretching of a spring.

The Assertion is True. Also, we know that for a given dimension, Young’s Modulus of Elasticity of steel is more than the Copper hence from equation (1). We can say that the tensile strength of Steel is more than that of Cu.

∴ The Reason is False.

Read and Learn More NEET Physics MCQs

Question 3. A wire of length L, area of cross-section A is hanging from a field support. The length of the wire changes to L₁ when mass M is suspended from its free end. The expression for Young’s modulus is :

1. \(\frac{\mathrm{Mg}\left(\mathrm{L}_1-\mathrm{L}\right)}{A L}\)
2. \(\frac{\mathrm{Mg} \mathrm{L}}{A L_1}\)
3. \(\frac{\mathrm{MgL}}{A\left(L_1-L\right)}\)
4. \(\frac{\mathrm{Mg} \mathrm{L}}{A L}\)

Answer: 1. \(\frac{\mathrm{Mg}\left(\mathrm{L}_1-\mathrm{L}\right)}{A L}\)

Given

A wire of length L, area of cross-section A is hanging from a field support. The length of the wire changes to L₁ when mass M is suspended from its free end.

Change in length, \(\Delta L=L_1-L\), Area, =A, force,

F = mg

Younger modules,\(\gamma =\frac{\text { Normal Stress }}{\text { Longitudinal Strain }}\)

⇒ \(\gamma =\frac{\frac{\mathrm{F}}{\mathrm{A}}}{\frac{\Delta \mathrm{L}}{\mathrm{L}}}\)

∴ \(\gamma=\frac{\left(\frac{\mathrm{Mg}}{A}\right)}{\left(\frac{\mathrm{L}_1-\mathrm{L}}{L}\right)}=\frac{\mathrm{Mg}\left(\mathrm{L}_1-\mathrm{L}\right)}{A \mathrm{~L}}\)

Question 4. When a block of mass M is suspended by a long wire of length L, the length of the wire becomes (L + l). The elastic potential energy stored in the extended wire is :

1. MgL
2. \(\frac{1}{2} M g l\)
3. \(\frac{1}{2} M g L\)
4. Mgl

Answer: 2. \(\frac{1}{2} M g l\)

Cross-Sectional Area = A

Original length = L

Elongation = l

⇒ \(\frac{\text { Energy stored }}{\text { Volume }} =\frac{1}{2} \text { stress } \times \text { strain }\)

⇒ \(\frac{E}{V} =\frac{1}{2} \times \frac{F}{A} \times \frac{\text { elongation }}{\text { length }}\)

⇒ \(\frac{E}{A L} =\frac{1}{2} \times \frac{m g}{A^{\prime}} \times \frac{l}{L}\)

∴ \(\mathrm{E} =\frac{1}{2} m g l\)

Question 5. Two wires are made of the same material and have the same volume. The first wire has cross-sectional area A and the second wire has cross-sectional area 3A. If the length of the first wire is increased by At on applying a force F, how much force is needed to stretch the second wire by the same amount?

1. 4F
2. 6F
3. 9F
4. F

Answer: 3. 9F

Given

Two wires are made of the same material and have the same volume. The first wire has cross-sectional area A and the second wire has cross-sectional area 3A. If the length of the first wire is increased by At on applying a force F

For wire (1), \(\Delta l=\left(\frac{F}{A \gamma}\right) 3 l\)  → Equation 1

For wire (2), \(\frac{F^{\prime}}{3 A}=\gamma \frac{\Delta l}{l}\)

⇒ \(\Delta l=\left(\frac{F^{\prime}}{3 A Y}\right) l\)  →   Equation 2

From eq. (1) and eq. (2),

we get, \(\Delta l =\frac{F}{A \gamma} 3 l-\left(\frac{F^{\prime}}{3 A Y}\right) l\)

∴ \(F^{\prime}\) =9 F

Question 6. The bulk modulus of a spherical object is B. If it is subjected to uniform pressure P, the fractional decrease in radius is:

1. \(\frac{P}{B}\)
2. \(\frac{B}{3 P}\)
3. \(\frac{3 P}{B}\)
4. \(\frac{P}{3 B}\)

Answer: 4. \(\frac{P}{3 B}\)

Bulk modulus (B) is the ratio of normal stress to volumetric strain,

B=\(\frac{\text { Normal stress }}{\text { Volumetric strain }}\)

=\(\frac{F / A}{\Delta V / V}=\frac{P}{\Delta V / V} \)

⇒ \(\frac{\Delta V}{V}=\frac{P}{B}\) [ P –  pressure on the object]  → Equation 1

Now from the question of fractional decrease in volumes

⇒ \(\frac{\Delta V}{V}=3 \frac{\Delta R}{R}\)    →  Equation 2

⇒ \({\left[V=\frac{4}{3} \pi R^3\right]}\)

From eq. (1) and (2), we get

∴ \(\frac{\Delta V}{V}=\frac{3 \Delta R}{R} = \frac{P}{B}\)

Question 7. The Young’s modulus of steel is twice that of brass. Two wires of the same length and the same area of cross-section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of:

1. 1: 2
2. 2: 1
3. 4: 1
4. 1: 1

Answer: 2. 2: 1

Given

The Young’s modulus of steel is twice that of brass. Two wires of the same length and the same area of cross-section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level,

Young’s modulus, \(\gamma=\frac{W. I}{A \Delta l}\)

I, A and \(\Delta l\) are same for both the wires

⇒ \(\gamma \propto W\)

⇒ \(\frac{\gamma_s}{\gamma_b}=\frac{W_s}{W_b}=\frac{2}{1}\)

∴ \(\mathrm{W}_s: \mathrm{W}_b=\) 2: 1

Question 8. The approximate depth of an ocean is 2700 m. The compressibility of water is 45.4 x 10^-11 Pa^-1 and the density of water is 10³ kg/m³. What fractional compression of water will be obtained at the bottom of the ocean?

1. 1.2 x 10^-2
2. 1.4×10^-2
3. 0.8×10^-2
4. 1.0×10^-2

Answer: 1. 1.2 x 10^-2

Depth of ocean, d=2700 m

Density of water, \(\rho=10^3 \mathrm{~kg} \mathrm{~m}^{-3}\)

Compressibility of water, \(\mathrm{K}=45.4 \times 10^{-11} \mathrm{~Pa}^{-1}\)

⇒ \(\frac{\Delta V}{V}\)=?

Excess pressure at the bottom, \(\Delta \mathrm{P}=\rho g d\)

=\(10^3 \times 10 \times 2700=27 \times 10^6 \mathrm{~Pa}\)

We know, \(\mathrm{B} =\frac{\Delta P}{(\Delta V / V)} \)

⇒ \(\frac{\Delta V}{(V)} =\frac{\Delta P}{B}=\mathrm{K} . \Delta \mathrm{P}\)

⇒ \((K \left.=\frac{1}{B}\right)\)

=\(45.4 \times 10^{-11} \times 27 \times 10^6\)

=\(1.2 \times 10^{-2}\)

Question 9. The copper of fixed volume V is drawn into a wire of length l. When the wire is subjected to a constant force F, the extension produced in the wire is Δl. Which of the following graphs is a straight line?

1. \( \Delta l versus \frac{1}{l} \)
2. \( \Delta l versus l^2 \)
3. \( \Delta l versus \frac{1}{l^2} \)
4. \( \Delta l versus l \)

Answer: 2. \(\Delta l versus l^2\)

⇒ \({ Young’s modulus }=\frac{\text { Longitudinal Stress }}{\text { Longitudinal Strain }}\)

Where, F= force applied

A = Area of cross-section

⇒ \(\gamma=\frac{\frac{F}{A}}{\frac{\Delta l}{l}}\)  →  Equation 1

⇒ \(\Delta l=\text { Change in length }\)

l= Original length And

V=A \(\times l=\text { Constant }\)

A = \(\frac{V}{l}\)  →  Equation 2

From (1) and (2),

we get, \(\gamma =\frac{F \times l \times l}{\Delta l \times V}\)

⇒ \(\Delta l =\frac{F}{V \times Y} \times l^2\)

⇒ \(\Delta l \propto l^2\)

∴ Where \(\mathrm{F}, \mathrm{V}, \gamma\) are constant

Question 10. The following four wires are made of the same material. Which of these will have the largest extension when the same tension is applied?

1. Length = 50 cm, diameter = 0.5 mm
2. Length =100 cm, diameter = 1 mm
3. Length = 200 cm, diameter = 2 mm
4. Length = 300 cm, diameter = 3 mm

Answer: 1. Length = 50 cm, diameter = 0.5 mm

We know that, \(\Delta L=\frac{F L}{A Y}\)

⇒ \(\Delta L \propto \frac{L}{d^2}\) { Since A=\(\frac{\pi d^2}{4}\}\)

This confirms that \(\Delta\) L will be the maximum for the wire when tension \(\frac{L}{A}\) maximum.

Question 11. In the ratio of diameters, lengths, and Young’s modulus, of steel and copper wires shown in the figure, are p, q, and s respectively, then the corresponding ratio of increase in their length would be:

1. \(\frac{7 q}{\left(7 s p^2\right)}\)
2. \(\frac{7 q}{\left(5 s p^2\right)}\)
3. \(\frac{2 q}{(5 s p)}\)
4. \(\frac{7 q}{(5 s p)}\)

Answer: 2. \(\frac{7 q}{\left(5 s p^2\right)}\)

Given

In the ratio of diameters, lengths, and Young’s modulus, of steel and copper wires shown in the figure, are p, q, and s respectively,

We know that,

Young’s modulus,\(\gamma =\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}\)

=\(\frac{\Delta \mathrm{FL}}{\pi \mathrm{D}^2 \Delta \mathrm{L}}\)  →  Equation 1

⇒ According to the questions,

⇒ \(\frac{\Delta \mathrm{L}_{\mathrm{S}}}{\Delta \mathrm{L}_{\mathrm{C}}}=\frac{\mathrm{F}_{\mathrm{S}}}{\mathrm{F}_{\mathrm{C}}} \cdot \frac{\mathrm{L}_{\mathrm{S}}}{\mathrm{L}_{\mathrm{C}}} \cdot \frac{\mathrm{D}_{\mathrm{C}}{ }^2 \mathrm{~L}_{\mathrm{S}}}{\mathrm{D}_{\mathrm{S}}{ }^2 \mathrm{~L}_{\mathrm{C}}}\)  → Equation – 2

Here, \(F_S=(5 m+2 m)\) g=7 m g

⇒ \(\mathrm{F}_{\mathrm{C}}=5 \mathrm{mg},\)=?,

⇒ \(\frac{\mathrm{D}_{\mathrm{S}}}{\mathrm{D}_{\mathrm{C}}}\)=p,

⇒ \(\frac{\mathrm{L}_{\mathrm{S}}}{\mathrm{L}_{\mathrm{C}}}=\mathrm{s}\)

Putting in eq. (2), we get,

⇒ \(\frac{\Delta \mathrm{L}_{\mathrm{S}}}{\Delta \mathrm{L}_{\mathrm{C}}} =\frac{7 \mathrm{mg}}{5 \mathrm{mg}} \times q+\left(\frac{1}{\mathrm{P}}\right)^2\left(\frac{1}{\mathrm{~S}}\right)\)

=\(\frac{7 q}{5 p^2 \mathrm{~S}}\)

NEET Physics For Gravitation Multiple Choice Questions

Question 1. A mass falls from a height ‘h’ and its time of fall ‘t’ is recorded in terms of time T of a simple pendulum. On the surface of Earth, it is found that t = 2 T. The entire set-up is taken on the surface of another planet whose mass is half of Earth and whose radius the same. The same experiment is repeated and corresponding times as t’ and T’:

1. \(t^{\prime}=\sqrt{2} \mathrm{~T}^{\prime}\)
2. \(t^{\prime}>2 \mathrm{~T}^{\prime}\)
3. \(t^{\prime}<2 \mathrm{~T}^{\prime}\)
4. \(t^{\prime}=2 \mathrm{~T}\)

Answer: 1. \(t^{\prime}=\sqrt{2} \mathrm{~T}^{\prime}\)

Force surface of Earth time taken is falling h distance t=\(\sqrt{\frac{2 h}{g}} \text { and } T=2 \pi \sqrt{\frac{l}{g}}\)

Given,

A mass falls from a height ‘h’ and its time of fall ‘t’ is recorded in terms of time T of a simple pendulum. On the surface of Earth, it is found that t = 2 T. The entire set-up is taken on the surface of another planet whose mass is half of Earth and whose radius the same.

t=\(2 T\)

⇒ \(\frac{t}{T}\)=2

For surface of other planet, \(g^{\prime}=\frac{g}{2}\)

Time taken in falling h distance, \(t^{\prime}=\frac{2 h}{g}=\sqrt{2} t\)

and \(T=2 \pi \sqrt{\frac{1}{g^{\prime}}}=\sqrt{2} T\)

Here \(\frac{t^{\prime}}{T^{\prime}}=\frac{\sqrt{2} t}{\sqrt{12} T}\)=2

∴ \(t^{\prime}=2 T^{\prime}\)

Question 2. The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are D_A, K_B and K_C respectively, AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then

1. \(t^{\prime}=\sqrt{2} \mathrm{~T}^{\prime}\)
2. \(t^{\prime}>2 \mathrm{~T}^{\prime}\)
3. \(t^{\prime}<2 \mathrm{~T}^{\prime}\)
4. \(t^{\prime}=2 \mathrm{~T}\)

Answer: 2. \(t^{\prime}>2 \mathrm{~T}^{\prime}\)

Given

The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are D_A, K_B and K_C respectively, AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure.

Point A is perihelion and C is aphelion.

So,\( V_A>V_B>V_C\)

As kinetic energy \(\mathrm{K}=(1 / 2) m v^2\) or \(K \propto v^2\)

So, \(K_A>K_B>K_C\)

Read and Learn More NEET Physics MCQs

Question 3. A planet moving along an elliptical orbit is closest to the sun at a distance of r₁ and farthest away at a distance of r₂. If V₁ and V₂ are the liner velocities at these points respectively, then the ratio \(\frac{v_1}{v_2}\) is:

1. \(\frac{r_2}{r_1}\)
2. \(\left(\frac{r_2}{r_1}\right)^2\)
3. \(\frac{r_1}{r_2}\)
4. \(\left(\frac{r_1}{r_2}\right)^2\)

Answer: 1. \(\frac{r_2}{r_1}\)

Using the law of conservation of angular moments \(m_1 v_1 =m_2 v_2 \)

⇒ \(m r_1 v_1 =m r_2 v_2 \)

⇒ \(r_1 v_1 =r_2 v_2 \)

∴ \(\frac{v_1}{v_2} =\frac{r_2}{r_1}\)

Question 4. The figure shows the elliptical orbit of a plant m about the sun S. The shaded area SCD is twice the shaded area SAB, if t₁ is the time for the planet to move from C to D and t₂ is the time to move from A to B, then:

1. \(t_1>t_2\)
2. \(t_1=4 t_2\)
3. \(t_1=2 t_2\)
4. \(t_1=t_2\)

Answer: 3. \(t_1=2 t_2\)

Applying Kepler’s law of planetary motion. \(\frac{d A}{d t}\) = constant

⇒ \(\frac{A_1}{t_1} =\frac{A_2}{t_2} \)

⇒ \( t_1 =\frac{A_1}{A_2} t_2 \)

Since, \(A_1 =2 A_2\)

Hence, \(t_1 =2 t_2\)

Question 5. The period of revolution of the planet A around the sun is 8 times that of B. The distance of A from the sun is how many times greater than that of B from the sun?

1. 5
2. 4
3. 3
4. 2

Answer: 2. 4

According to Kelper’s third law,

⇒ \(T^2 \propto r^3\)

Where, T= period of revolution

r= Semi-major axis

⇒ \(\frac{T_A^2}{T_B^2} =\frac{r_A^3}{r_B^3}\)

⇒ \( \frac{r_A}{r_B} =\left(\frac{T_A}{T_B}\right)^{2 / 3} \)

=\( (8)^{\frac{2}{3}}\)

=\(2^{3 \times \frac{2}{3}}\) =4

or \(r_A =4 r_B\)

Question 6. The distances of the two planets from the sun are 10¹³ and 10¹² m respectively. The ratio of periods of these two planets is:

1. \(\frac{1}{\sqrt{10}}\)
2. 100
3. 10 \(\sqrt{10}\)
4. 1 \(\sqrt{10}\)

Answer: 3. 10 \(\sqrt{10}\)

According to Kepler’s third law (or the law of periods) \(T^2 \propto r^3\)

Here, \(r_1=10^{13} \mathrm{~m}, r_2=10^{12} \mathrm{~m}\)

⇒ \(\frac{T_1^3}{T_2^2}=\frac{r_1^3}{r_2^3}=\frac{\left(10^{13}\right)^3}{\left(10^{12}\right)^3}\)

or \(\frac{T_1^2}{T_2^2}=\frac{10^{39}}{10^{36}}=10^3 \)

or \(\frac{T_1}{T_2}=10 \sqrt{10}\)

Question 7. A planet is moving in an elliptical orbit around the Sun. If. T, V, E and L stand respectively for their kinetic energy, gravitational potential energy, total energy and magnitude of angular momentum about the centre of force, which of the following is correct?

1. T is conserved.
2. V is always positive.
3. E is always negative.
4. T is conserved but the direction of vector L changes continuously.

Answer: 3. E is always negative.

In a circular or elliptical orbital motion of a planet, angular momentum is conserved. In an attractive field, potential energy and total energy are negative. Kinetic energy increases with an increase in velocity. If the motion is in a plane, the direction of L does not change.

Question 8. The largest and the shortest distance of the Earth from the sun are r₁ and r₂. Its distance from the sun when it is perpendicular to the major axis of the orbit drawn from the sun is

1. \(\frac{r_1+r_2}{4}\)
2. \(\frac{r_1+r_2}{r_1-r_2}\)
3. \(\frac{2 r_1 r_2}{r_1+r_2}\)
4. \(\frac{r_1+r_2}{3}\)

Answer: 3. \(\frac{2 r_1 r_2}{r_1+r_2}\)

Applying the properties of ellipse,

we have, \(\frac{2}{R} =\frac{1}{r_1}+\frac{1}{r_2}\)

=\(\frac{r_1+r_2}{r_1 r_2}\)

∴ \(\mathrm{R} =\frac{2 r_1 r_2}{r_1+r_2}\)

Question 9. Two astronauts are floating in gravitation-free space after having lost contact with their spaceship. The two will:

1. keep floating at the same distance between them
2. move towards each other
3. move away from each other
4. will become stationary

Answer: 2. move towards each other

Both the astronauts are in the condition of weightless. The gravitational force between them pulls towards each other

Question 10. Kepler’s third law states that the square of the period of revolution (7) of a planet around the sun, is proportional to the third power of the average distance r between the sun and planet is T² = Kr³ here K is constant. If the masses of the sun and planet are M and m respectively, then as per Newton’s law of gravitation force of attraction between them is:\(\mathrm{F}=\frac{\mathrm{GM} m}{r^2}\), here G gravitational constant. The relation between G and K is described as:

1. \(\mathrm{GK}=4 \pi^2\)
2. \(\mathrm{GMK}=4 \pi^2\)
3. \(\mathrm{K}=\mathrm{G}\)
4. K=\(\frac{1}{G}\)

Answer: 2. \(\mathrm{GMK}=4 \pi^2\)

Given

Kepler’s third law states that the square of the period of revolution (7) of a planet around the sun, is proportional to the third power of the average distance r between the sun and planet is T² = Kr³ here K is constant. If the masses of the sun and planet are M and m respectively, then as per Newton’s law of gravitation force of attraction between them is:\(\mathrm{F}=\frac{\mathrm{GM} m}{r^2}\), here G gravitational constant.

Let the mass of the Sun = M

and mass of planet = m

Then the gravitational force between them, \(\mathrm{F}=\frac{\mathrm{GM} m}{r^2}\)

where, r= distance between sun and planet.

The above force provided the centripetal force,

⇒ \(\frac{\mathrm{GM} m}{r^2}=\frac{m v^2}{2}\)

⇒ \(\sqrt{\frac{\mathrm{GM}}{r}}\)=v

We know that the period of a planet is,

T =\(\frac{2 \pi r}{v}\)

T =\(\frac{2 \pi r}{\sqrt{\frac{\mathrm{GM}}{r}}}\)

⇒ \(T^2=\frac{4 \pi^2 r^2}{\frac{\mathrm{GM}}{r}}=\frac{4 \pi^2 r^3}{\mathrm{GM}}\) → Equation 1

According to Kepler’s third law, \(T^2 \propto r^3 \)  →  Equation 2

⇒ \(T^2=k r^3 \)

From eq. (1) and (2),

⇒ \(\frac{4 \pi^2 r^3}{\mathrm{GM}} =k r^3 \)

∴ \(\mathrm{GMK} =4 \pi^2\)

Question 11. The dependence of the intensity of gravitational field (E) of Earth distance (r) from the centre of Earth is correctly represented by:

Answer: 2.

Option (B) is the graph of dependence of the intensity of gravitational field (E) of Earth with distance (r) from the centre of Earth

Question 12. Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of radius R (r is measured from the centre of the spherical shell)?

Answer: 2.

Question 13. A body projected vertically from the Earth reaches a height equal to the Earth’s radius before returning to the Earth. The power exerted by the gravitational force is greatest:

1. at the instant just before the body hits the Earth
2. it remains constant all through
3. at the instant just after the body is projected
4. at the height position of the body

Answer: 1. at the instant just before the body hits the Earth

We know that, P=\(\vec{F} \cdot \vec{v}=F v \cos \theta\)

Power will be maximum when velocity and \(cos \theta\) will be maximum.

Question 14. Two spheres of masses m and M are situated in the air and the gravitational force between them is F. The space around the masses is now filled with a liquid of specific gravity 3. The gravitational force will now be:

1. 3F
2. F
3. \(\frac{F}{3}\)
4. \(\frac{F}{9}\)

Answer: 2. F

The gravitational force does not depend upon the medium in which objects are placed.

Question 15. Gravitational force is required for:

1. stirring of liquid
2. convection
3. conduction
4. radiation

Answer: 2. convection

Fluid sections become lighter and flow upward as temperature rises, while heavier and denser fluid portions migrate lower. As a result, particles move up and down depending on their weight and gravity. As a result, the existence of a gravitational field is essential in natural convection heat transfer

Question 16. A body of weight 72 N moves from the surface of Earth at a height half of the radius of Earth, then the gravitational force exerted on it will be:

1. 36 N
2. 32 N
3. 144 N
4. 50 N

Answer: 2. 32 N

⇒ \(\mathrm{F}_{\text {surface }} =F \frac{M m}{R_e^2}\)

⇒ \(\mathrm{~F}_{R_e / 2} =G \frac{M m}{\left(R_e+R_e / 2\right)^2}\)

=\(\frac{4}{9} \times F_{\text {surface }}\)

=\(\frac{4}{9} \times 72=32 \mathrm{~N}\)

Question 17. Two particles of equal mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is:

1. \(\frac{1}{2} \sqrt{\frac{G m}{R}}\)
2. \(\sqrt{\frac{4 G m}{R}}\)
3. \(\frac{1}{2 R} \sqrt{\frac{1}{G m}}\)
4. \(\sqrt{\frac{G m}{R}}\)

Answer: 1. \(\frac{1}{2} \sqrt{\frac{G m}{R}}\)

Force between the two masses, F = \(-G \frac{m m}{4 R^2}\)

This force will provide the necessary centripetal force for the masses to go around a circle, then,

⇒ \(\frac{G m m}{4 R^2} =\frac{m v^2}{R}\)

⇒ \(v^2 =\frac{G m}{4 R}\)

v =\(\frac{1}{2} \sqrt{\frac{G m}{R}}\)

Question 18. The Earth (mass = 6 x 1024 kg) revolves around the sun with an angular velocity of 2 x 10^-7 rad/s in a circular orbit of radius 1.5 x 10⁸ km. The force exerted by the sun on the Earth, in Newton is:

1. 36 x 10²¹
2. 27 x 10³⁹
3. zero
4. 18 x 10²³

Answer: 1. 36 x 10²¹

Give: mass(m) =\(6 \times 10^{24} \mathrm{~kg}\)

angular velocity \((\omega) =2 \times 10^{-7} \mathrm{rad} / \mathrm{s}\) and

radius(r) =\(1.5 \times 10^8 \mathrm{~km}\)

=\(1.5 \times 10^{11} \mathrm{~m}\)

Force exerted on the Earth =\(\mathrm{mRw}^2\)

=\(\left(6 \times 10^{24}\right) \times\left(1.5 \times 10^{11}\right) \times\left(2 \times 10^{-7}\right)^2\)

=\(36 \times 10^{21} \mathrm{~N}\)

Question 19. If the gravitational force between two objects were proportional to 1 /R (and not as I /R²), where R is the distance between them, then a particle in a circular path (under such a force) would have its orbital speed v, proportional to:

1. R
2. R° (independent of R)
3. 1/R²
4. 1/R

Answer: 2. R° (independent of R)

Centripetal force (F)=\(\frac{m v^2}{R}\) and the gravitational force \((\mathrm{F})=\frac{G M m}{R}=\frac{G M m}{R}, (where R^2 \rightarrow R )\).

Since \(\frac{m v^2}{R}=\frac{G M m}{R}\) therefore v=\(\sqrt{G M}\).

Thus velocity v is independent of R.

Question 20. If the mass of the Earth were ten times smaller and the universal gravitational constant were ten times larger in magnitude, which of the following is not correct?

1. The period of a simple pendulum on the Earth would decrease
2. Walking on the ground would become more difficult
3. Raindrops will fall faster
4. ‘g’ on the Earth will not change

Answer: 1. The Period of a simple pendulum on the Earth would decrease

Let \(M_e\) =riginal mass of Earth

G =Gravitational constant

Then from question, Mass of Earth \(M_E^{\prime}=\frac{M_E}{10}\)

New gravitational constant \(G^{\prime}\)=10 G

We know that, Acceleration due to gravity,

g=\(\frac{G M_E}{R^2}\)

⇒ \(M_E\) = mass of Earth

R = radius of Earth

New acceleration due to gravity u,

⇒ \(g^{\prime} =\frac{G^{\prime} M_E}{R^2}\)

=\(\frac{10 M_E G}{R L}\)

⇒ \(g^{\prime} =10 \mathrm{~g}\)

We also know that time pursued by a simple pendulum is,

T=\(2 \pi \sqrt{\frac{1}{g}}\)

⇒ \(T \propto \sqrt{\frac{1}{g}}\)

∴ This confirms that the period of the pendulum also decreases with the increase in g.

Question 21. A spherical planet has a mass of M_P and a diameter of D_P. A particle of mass m falling freely near the surface of this planet will experience acceleration due to gravity is

1. \(\frac{\Delta G M_P}{D_P^2}\)
2. \(\frac{G M_p m}{D_P^2}\)
3. \(\frac{G M_P m}{D_P^2}\)
4. \(\frac{4 G M_P m}{D_P^2}\)

Answer: 1. \(\frac{\Delta G M_P}{D_P^2}\)

We know that, Gravitational Force, F =\(\frac{G M_e m}{R^2}\)

F =\(\frac{G M_P m}{\left(D_P / 2\right)}\)

=\(\frac{4 G M_P m}{D_P^2}\)

And, F=m a

a =\(\frac{F}{m}\)

=\(\frac{\Delta G M_P m}{P^2}\)

=\(\frac{\Delta G M_P}{\Delta p^2}\)

Question 22. Imagine a new planet having the same density as that of Earth but it is 3 times bigger than the Earth in size. If the acceleration due to gravity on the surface of Earth is g and that on the surface of the new planet is g’ then:

1. \(g^{\prime}=\frac{g}{9}\)
2. \(g^{\prime}\)=27 g
3. \(g^{\prime}\)=9 g
4. \(g^{\prime}\)=3 g

Answer: 4. \(g^{\prime}\)=3 g

g =\(\frac{G M}{R^2}=\frac{G \frac{4}{3} \pi R^2 \rho}{R^2}\)

=\(\frac{4}{3} G \pi R \rho\)

∴ \(g^{\prime} =\frac{4}{3} G \pi(3 R) \rho\) =3 g

Question 23. The density of a newly discovered plant is twice that of Earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the Earth. If the radius of the Earth is R, the radius of the planet would be:

1. 2R
2. 4R
3. \(\frac{1}{4} R\)
4. \(\frac{1}{2} R\)

Answer: 4. \(\frac{1}{2} R\)

We know that, \(\frac{G M_p}{R_p^2} =\frac{G M_e}{R_e^2}\)

⇒ \(\frac{G \times \frac{4}{3} \pi R_p^3 \rho_p}{R_p^2} =\frac{G \times \frac{4}{3} \pi R_e^3 \rho_e}{R_e^2}\)

we get, Given,

⇒ \(R_p \rho_p =R_e \rho_e \)

⇒ \(\rho_p =2 \rho_e\)

then \(R_p \times 2 \rho_e =R_e \rho_e\)

∴ \(R_p =\frac{R_e}{2}=\frac{R}{2}\)

Question 24. The acceleration due to gravity on planet A is 9 times the acceleration due to gravity on planet B. A man jumps to a height of 2 m on the surface of A. What is the height of the jump by the same person on the plane B?

1. 2/9 m
2. 18 m
3. 6 m
4. 2/3 m

Answer: 2. 18 m

Height Of Jump on the planet B

= \(\frac{g_A}{g_B} \times\)Height Of Jump on the planet A

= 2 x 9 = 18m

Question 25. What will be the formula of mass of the Earth in terms of g, R And G?

1. \(G \frac{R}{g}\)
2. \(g \frac{R^2}{G}\)
3. \(g^2 \frac{R}{G}\)
4. \(G \frac{g}{R}\)

Answer: 2. \(g \frac{R^2}{G}\)

As We Know, F =\(\frac{G M m}{R^2}\)

mg =\(\frac{G M m}{R^2}\)

g =\(\frac{G M}{R^2}\)

M =\(\frac{g R^2}{G}\)

Where, M = mass of earth

g = Gravitational Acceleration

R = Radius of Earth

G = Gravitational constant

Question 26. The acceleration due to gravity and mean density of the Earth \(rho\) are related by which of the following relations? (where G is the gravitational constant and R is the radius of the Earth.)

1. \(\rho=\frac{3 g}{4 \pi G R}\)
2. \(\rho=\frac{3 g}{4 \pi G R^3}\)
3. \(\rho=\frac{4 \pi g R^2}{3 G}\)
4. \(\rho=\frac{4 \pi g R^3}{3 G}\)

Answer: 1. \(\rho=\frac{3 g}{4 \pi G R}\)

Acceleration Due to Gravity g =\(G \times \frac{M}{R^2}\)

=G \(\frac{(4 / 3) \pi R^3 \times \rho}{R^2}\)

=G \(\times \frac{4}{3} \pi R \times \rho\)

or \(\rho =\frac{3 g}{4 \pi G R}\)

Question 27. The radius of Earth is about 6400 km and that of Mars is 3200 km. The mass of the Earth is about 10 times the mass of Mars. An object weighs 200 N on the surface of the Earth. Its weight on the surface of Mars will be:

1. 20 N
2. 8 N
3. 80 N
4. 40 N

Answer: 3. 80 N

Given: radius of Earth \(\left(R_e\right)\)=6400 \(\mathrm{~km}\); the radius of Mars \(\left(R_m\right)=3200 \mathrm{~km}\); the mass of Earth \(\left(M_e\right)=10 M_m\) and weight of the object on Earth \(/left(W_e)=200 \mathrm{~N}\).

⇒ \(\frac{W_m}{W_e} =\frac{m g_m}{m g_e}\)

=\(\frac{M_m}{M_e} \times\left(\frac{R_e}{R_m}\right)^2\)

=\(\frac{1}{10} \times(2)^2=\frac{2}{5}\)

∴ \(W_m=W_e \times \frac{2}{5}=200 \times 0.4=80 \mathrm{~N}\)

Question 28. A particle of mass ‘w’ is projected with a velocity v = kV_e (k < 1) from the surface of the Earth. (v_e = Escape velocity) The maximum height above the surface reached by the particle is

1. \(\mathrm{R}\left(\frac{\mathrm{K}}{1-k}\right)^2\)
2. \(\mathrm{R}\left(\frac{\mathrm{K}}{1+k}\right)^2\)
3. \(\frac{\mathrm{R}^2 k}{1+k}\)
4. \(\frac{\mathrm{R} k^2}{1-k^2}\)

Answer: 4. \(\frac{\mathrm{R} k^2}{1-k^2}\)

Given, v=\(\mathrm{K} v_e\), H =?

At max height H \(\mathrm{KE} =\mathrm{PE}\)

⇒ \(\mathrm{KE} =\frac{1}{2} m v^2\)

=\(\frac{1}{2} m \mathrm{~K}^2 \mathrm{~V}_e{ }^2 \)

⇒ \(\mathrm{PE} =\frac{\mathrm{GM} m}{\mathrm{R}+\mathrm{H}}\)

⇒ \(\mathrm{v}_e{ }^2 =\frac{2 \mathrm{GM}}{\mathrm{R}}\)

⇒ \(\frac{\mathrm{K}^2}{\mathrm{R}} =\frac{1}{\mathrm{R}+\mathrm{H}}\)

⇒ \(\mathrm{R}+\mathrm{H} =\frac{\mathrm{R}}{\mathrm{K}^2}\)

H =\(R\left(\frac{1}{\mathrm{~K}^2}-1\right)\)

=\(R\left(\frac{1-\mathrm{K}^2}{\mathrm{~K}^2}\right)\)

Question 29. The dependence of acceleration due to gravity g on the distance f from the centre of Earth assumed to be a sphere of radius R of uniform density is as shown in the figure below:

Answer: 4.

g \(\propto r(\text { if } r<R)\)

And \(\mathrm{g} \propto \frac{1}{r^2}(\text { If } r>R)\)

The correct figure is D.

Question 30. What is the depth at which the value of acceleration due to gravity becomes 1/n times the value at the surface of Earth (Radius of Earth = R)?

1. \(\frac{\mathrm{R}}{n^2}\)
2. \(\frac{\mathrm{R}(n-1)}{n}\)
3. \(\frac{\mathrm{Rn}}{(n-1)}\)
4. R.n

Answer: 2. \(\frac{\mathrm{R}(n-1)}{n}\)

Radius of Earth = R

Let at depth d, gravitational acceleration become \(\frac{g}{n}\)

⇒ \(g_d =g_o\left(1-\frac{d}{R}\right)\)

⇒ \(\frac{g_o}{n} =g_o\left(1-\frac{d}{R}\right)\)

⇒ \(\frac{1}{n} =1-\frac{d}{R}\)

⇒ \(\frac{d}{R} =1-\frac{1}{n}\)

⇒ \(\frac{d}{R} =\left(\frac{n-1}{n}\right)\)

d =\(\left(\frac{n-1}{n}\right)\) R .

Question 31. A body weighs 72 N on the surface of the Earth. What is the gravitational force on it, at a height equal to half of the radius of the Earth?

1. 32N
2. 30N
3. 24N
4. 48N

Answer: 1. 32N

Given, W = mg = 72 N

On the surface of the Earth. At a height equal to half of the radius of Earth.h=\(\frac{\mathrm{R}}{2}\)

Acceleration due to gravity,

⇒ \(g^{\prime} =g\left(\frac{\mathrm{R}}{\mathrm{R}+h}\right)^2\)

= \(\mathrm{g}\left(\frac{\mathrm{R}}{\mathrm{R}+\frac{\mathrm{R}}{2}}\right)^2\)

= \(g\left(\frac{4 \mathrm{R}^2}{9 \mathrm{R}^2}\right)\)

⇒ \(g^{\prime} =g \times \frac{4}{9}\)

⇒ \(m g^{\prime} =m g \times \frac{4}{9}\)

= \(\frac{4}{9} \times 72 \)

∴ \(m g^{\prime} =32 \mathrm{~N}\)

Question 32. A body weighs 200 N on the surface of the Earth. How much will it weigh halfway down to the centre of the Earth?

1. 200N
2. 250N
3. 100N
4. 150N/kg

Answer: 3. 250N

Below the surface of Earth, acceleration due to gravity is: \(g^{\prime}=\left(1-\frac{d}{R}\right)\)   →   Equation 1

Where, d= depth, R: is the radius of Earth g = acceleration due to gravity Multiply m in both sides of the equations

⇒ \(Given, m g^{\prime}=m g\left(1-\frac{d}{R}\right)\)  →   Equation 2

Given, W=m g=200

d=\(\frac{R}{2}\)

Putting these values in eq. (2), we get

⇒ \(m g^{\prime} =200\left(1-\frac{R}{\frac{2}{R}}\right)=200\left(1-\frac{1}{2}\right)\)

=\(200 \times \frac{1}{2}\)

=100 N

∴ The body will weigh 100 N halfway down to the centre of Earth.

Question 33. The acceleration due to gravity at a height of 1 km above the Earth is the same as at a depth d below the surface of the Earth. Then:

1. d=\(\frac{1}{2} \mathrm{~km}\)
2. d=1 \(\mathrm{~km}\)
3. d=\(\frac{3}{2} \mathrm{~km}\)
4. d=2 \(\mathrm{~km}\)

Answer: 4. d=2 \(\mathrm{~km}\)

Given that acceleration due to gravity at depth d is,

⇒ \(g^{\prime}=g\left(1-\frac{d}{R}\right)\)  →  Equation 1

Where, R=radius of Earth

And Acceleration due to gravity at height h is,

⇒ \(g^{\prime \prime}=g\left(1-\frac{2 h}{R}\right)\)   →  Equation 2

According to question,\( g^{\prime} =g^{\prime \prime}\) and h=1 \(\mathrm{~km}\)

⇒ \(g\left(1-\frac{d}{R}\right) =g\left(1-\frac{2 h}{R}\right)\)

(putting h=1 )

⇒ \(g\left(1-\frac{d}{R}\right) =g\left(1-\frac{2}{R}\right)\)

⇒ \(\frac{d}{R} =\frac{2}{R}\)

d =2 km

Question 34. Starting from the centre of the Earth having radius R, the variation of due to gravity) is shown by:

Answer: 2.

We know that acceleration due to gravity below \(g_d=g\left(1-\frac{d}{R}\right)\)

and acceleration due to gravity at height h is \(g_h=g\left(\frac{R^2}{(R+h)^2}\right)\)

From the above equation, it is clear that the value of g increases from the centre of the maximum at the surface and then decreases

g=\(\left(\frac{G M_e}{R_e^3}\right) r, \text { for } 0<r \leq R_e\)

⇒ \(g \propto r \)

⇒ \(g=\frac{G M_e}{r^2}\), for \(r<R_e \)

∴ \(g \propto \frac{1}{r^2}\)

Question 35. The height at which the weight of a body becomes 1/16th its weight on the surface of Earth (radius R), is:

1. 5 R
2. 15 R
3. 3 R
4. 4 R

Answer: 3. 3 R

According to the question, \(\frac{G M \not m}{(R+h)^2}=\frac{1}{16} \frac{G M \not h}{R^2}\)

Where, R= Radius of Earth

⇒ \(\frac{1}{(\mathrm{R}+h)^2}=\frac{1}{16 R^2}\)

⇒ \(\frac{R}{R+h}=\frac{1}{4}\)

⇒ \(\frac{R+h}{R}\)=4

∴ h = 3R

Question 36. A body of mass 60 g experiences a gravitational force of 3.0 N when placed at a particular point. The magnitude of the gravitational field intensity at that point is:

1. 15 N/kg
2. 20N/kg
3. 150N/kg
4. 0.05 N/kg

Answer: 1. 15 N/kg

Given: Mass of the body, m= 60 g = 0.06 kg

Gravitational force, F =3.0 N

The gravitational field intensity is written as; \(I_g=\frac{F}{m}\) →  Equation 1

Now, On putting all the given values in equation (1) we have,

⇒ \(I_g=\frac{3.0}{0.06}\)

∴ \(I_g=50 \mathrm{~N} / \mathrm{kg}\)

Question 37. A particle of mass M is situated at the centre of a spherical shell of the same mass and radius a. ‘The magnitude of the gravitational potential at a point situated at \(\frac{a}{2}\) distance from the centre, will be:

1. \(\frac{2 G M}{a}\)
2. \(\frac{3 G M}{a}\)
3. \(\frac{4 G M}{a}\)
4. \(\frac{G M}{a}\)

Answer: 2. \(\frac{3 G M}{a}\)

⇒ \(v_P =v_{\text {sphere }}+v_{\text {particle }}\)

⇒ \(v_P =\frac{G Y}{a}+\frac{G Y}{a / 2} \)

=\(\frac{G Y}{a}+\frac{2 G y}{a}=\frac{3 G Y}{a}\)

Question 38. The work done to raise a mass m from the surface of the Earth to a height h, which is equal to the radius of the Earth, is:

1. \(\frac{3}{2} m g R\)
2. mgR
3. 2 \(\mathrm{mgR}\)
4. \(\frac{1}{2} m g R\)

Answer: 4. \(\frac{1}{2} m g R\)

Work done = Change in potential energy

=\(u_f-u_i=\frac{-G M m}{(R+h)}-\left(\frac{-G M m}{R}\right)\)

where, \(\mathrm{M}\) is the mass of Earth and \(\mathrm{R}\) is the radius of Earth.

⇒ \(\mathrm{W}=G M m\left[\frac{1}{R}-\frac{1}{(R+h)}\right]\)

Now, h=R

W=\(G M m\left[\frac{1}{R}-\frac{1}{2 R}\right]=\frac{G M m}{2 R}\)

W=\(\frac{m g R}{2} g=\frac{G M}{R^2}\)

Question 39. At what height from the surface of Earth are the gravitation potential and the value of g – 5.4 * 10⁷ J kg^-2 and 6.0 ms^-2 respectively? [Take, the radius of Earth as 6400 km.]

1. 1600 km
2. 1400 km
3. 2000 km
4. 2600 km

Answer: 4. 2600 km

We know that Gravitational potential at height h from the surface of Earth is v=\(-\frac{G M}{R+h}\)

Here, v=\(-\frac{G M}{R+h}=-5.4 \times 10^7\)  →  Equation 1

Given an acceleration due to gravity of height ft from the surface of Earth,

g=\(\frac{G M}{(R+h)^2}\)=6  →  Equation 2

Divide eq. (1) by eq. (2),

=\(\frac{5.4 \times 10^7}{(R+h)}\)=6

⇒ R+h=9000 km =9000-6400

h =2600 km

Question 40. An infinite number of bodies, each of mass 2 kg are situated on the x-axis at distances 1 m, 2 m, 4 m, and 8 m, respectively from the origin. The resulting gravitational potential due to this system at origin will be:

1. -G
2. \(-\frac{8}{3} G\)
3. \(-\frac{4}{3} G\)
4. -4 G

Answer: 4. -4 G

The resulting gravitational potential due to the system again is,

V =\(-2 G\left[1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots\right]\)

=\(-2 G\left[1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\ldots\right]\)

V =\(-2 G\left(1-\frac{1}{2}\right)^{-1} \)

V =\(\frac{-2 G}{\left(1-\frac{1}{2}\right)}\)

V =\(\frac{-2 G}{\frac{1}{2}}\)=-4 G

V =-4 G

Question 41. A body of mass ‘m’ is taken from the Earth’s surface to a height equal to twice the radius (R) of the Earth. The change in potential energy of the body will be:

1. 3 mgR
2. \(\frac{1}{3} m g R\)
3. mg 2R
4. \(\frac{2}{3} m g R\)

Answer: 4. \(\frac{2}{3} m g R\)

Gravitational potential energy at any point at a distance r from the centre of the Earth is, U=\(-\frac{G M m}{r}\)

where M and m are masses of the Earth and the body respectively.

At the surface of the Earth, r =R ;

⇒ \(U_i =-\frac{G M m}{R}\)

At a height of h from the surface,

r=R+h=R+2 R=3 R

h = 2R (Given)

⇒ \(U_f =-\frac{G M m}{3 R}\)

Change in potential energy,

⇒ \(\Delta U =U_f-U_i\)

=\(-\frac{G M m}{3 R}-\left(-\frac{G M m}{R}\right)\)

=\(\frac{G M m}{R}\left(1-\frac{1}{3}\right)\)

=\(\frac{2}{3} \frac{G M m}{R}=\frac{2}{3} m g R\)

∴ \((g=\frac{G M}{R^2}\)

Question 42. A body of mass m is placed on Earth’s surface which is taken from Earth’s surface to a height of h = 3R, then the change in the gravitational potential energy is:

1. \(\frac{m g R}{4}\)
2. \(\frac{2}{3} m g R\)
3. \(\frac{3}{4} m g R\)
4. \(\frac{m g R}{2}\)

Answer: 3. \(\frac{3}{4} m g R\)

change in Gravitational Potential energy

= final energy – initial energy

=\(-\frac{G M m}{4 R}+\frac{\mathrm{G} M m}{R}\)

=\(-\frac{G M m}{4 R}\left[1-\frac{1}{4}\right]\)

=\(\frac{3}{4} \frac{G M m}{4 R}\)

=\(\frac{3}{4} \frac{G M}{R^2} m R=\frac{3}{4} g m R\)

Question 43. A particle of mass m is thrown upwards from the surface of the Earth, with a velocity u. The mass and the radius of the Earth are, respectively, M and R. G is gravitational contact and g is acceleration due to gravity on the the surface of the Earth. The minimum value of u so that the particle does not return to Earth, is:

1. \(\sqrt{\frac{2 G M}{R}}\)
2. \(\sqrt{\frac{2 G M}{R^2}}\)
3. \(\sqrt{2 g R^2}\)
4. \(\sqrt{\frac{2 G M}{R^2}}\)

Answer: 1. \(\sqrt{\frac{2 G M}{R}}\)

Given

A particle of mass m is thrown upwards from the surface of the Earth, with a velocity u. The mass and the radius of the Earth are, respectively, M and R. G is gravitational contact and g is acceleration due to gravity on the the surface of the Earth.

We know that Escape velocity, \(v_e=\sqrt{2 g R}\)

since, GM =\(9 \mathrm{R}^2 \)

=\(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}^2} \times \mathrm{R}}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)

Question 44. The ratio of escape velocity on Earth (v_e) to the escape velocity at a planet (v_p) whose radius and mean density are twice that of Earth is:

1. 1: 2 \(\sqrt{2}\)
2. 1: 4
3. 1: \(\sqrt{2}\)
4. 1: 2

Answer: 1. 1: 2 \(\sqrt{2}\)

Since, escape velocity, \(v_e =\sqrt{\frac{2 G M}{R}}=\sqrt{\frac{2 G}{R}\left(\frac{4}{3} \pi R^3 \rho\right)}\)

⇒ \(v_e =R \sqrt{\rho}\)

∴ Ratio =\(1: 2 \sqrt{2}\)

Question 45. A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would Earth (mass = 5.98 x 10²⁴ kg) have to be compressed to be a black hole?

1. 10^-9 m
2. 10^-6 m
3. 10^-2 m
4. 100 m

Answer: 3. 10^-2 m

In this question compare escape relatives with the velocity of light c.

Escape velocity \(v_e=\sqrt{\frac{2 G M}{R}}\)

R= New radius of the Earth

Since,\( v_e=c\)

c=\(\sqrt{\frac{2 G M}{R}}\)

⇒ \(c^2=2 \frac{G M}{R}\)

R =\(\frac{2 G M}{c^2}\)

=\(\frac{2 \times 6.07 \times 10^{-11} \times 6 \times 10^{24}}{\left(3 \times 10^8\right)^2}\)

=\(\frac{2 \times 6.07 \times 10^{-11} \times 6 \times 10^{24}}{9 \times 10^{16}}\)

=\(\frac{4 \times 6.07}{3} \times 10^{-3}\)

=0.889 \(\times 10^{-2}\)

⇒ \(10^{-2} \mathrm{~m}\)

Here, gravitational constant G=\(6.07 \times 10^{-11}\)

Mass of Earth M=\(6 \times 10^{14} \mathrm{~kg}\)

Question 46. The radius of the planet is twice the radius of Earth. Both have almost equal average mass densities v_p and v_E are escape velocities of the planet and the Earth respectively, then:

1. v_p = 1.5 v_E
2. v_p = 2 v_E
3. v_E= 3 v_p
4. v_E= 1.5 v_p

Answer: 2. v_p = 2 v_E

According to the question,

⇒ \(R_P=2 R_E, \rho_E=\rho_P\)

Escape velocity of Earth, \(v_E =\sqrt{\frac{2 G M_E}{R_E}}\)

=\(\sqrt{\frac{2 G}{R_E}\left(\frac{4}{3} \pi R_E{ }^3 \rho_E\right)}\)

=\(R_E \sqrt{\frac{8}{3} \pi G \rho_E}\)  → Equation 1

Similarly, the Escape velocity of the planet

⇒ \(v_P=\sqrt{\frac{2 G M_P}{R_P}}\)

⇒ \(v_P=\sqrt{\frac{2 G}{R_P}\left(\frac{4}{3} \pi R_p^3 \rho_p\right)}\)

⇒ \(v_P=R_P \sqrt{\frac{8}{3} \pi G \rho_p}\)  →  Equation 2

from eq. (1) and eq. (2), we get,

⇒ \(\frac{v_E}{v_P} =\frac{R_E}{R_P} \sqrt{\frac{\rho_E}{\rho_P}}\)

=\(\frac{R_E}{2 R_E} \sqrt{\frac{\rho_Q}{\rho_E}}=\frac{1}{2}\)

∴ \(v_p =2 v_E\)

Question 47. A particle of mass W is kept at rest at a height 3R from the surface of Earth, where ‘R’ is the radius of Earth and ‘M is the mass of Earth. The minimum speed with which it should be projected, so that it does not return, is (g is the acceleration due to gravity on the surface of Earth):

1. \(\left(\frac{G M}{2 R}\right)^{\frac{1}{2}}\)
2. \(\left(\frac{g R}{4}\right)^{\frac{1}{2}}\)
3. \(\left(\frac{2 g}{R}\right)^{\frac{1}{2}}\)
4. \(\left(\frac{G M}{R}\right)^{\frac{1}{2}}\)

Answer: 1. \(\left(\frac{G M}{2 R}\right)^{\frac{1}{2}}\)

Escape velocity \(v_e=\sqrt{\frac{2 \mathrm{GM}}{(\mathrm{R}+h)}}\)

From the question h=3 R

⇒ \(v_e^{\prime} =\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}+3 \mathrm{R}}}\)

=\(\sqrt{\frac{2 G M}{4 R}}\)

=\(\sqrt{\frac{G M}{2 R}}=\sqrt{\frac{g R}{2}}\)

∴ where, g =\(\frac{G M}{R^2}\)

Question 48. The Earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of the Earth. The escape velocity of a body from this platform is fv, where v is its escape velocity from the surface of the Earth. The value of f is:

1. \(\frac{1}{2}\)
2. \(\sqrt{2}\)
3. \(\frac{1}{\sqrt{2}}\)
4. \(\frac{1}{3}\)

Answer: 3. \(\frac{1}{\sqrt{2}}\)

We know that Escape velocity,

⇒ \(v_e=\sqrt{2 g R}\)

Escape velocity of the body from the platform,

⇒ \(\mathrm{P} \cdot \mathrm{E}+\mathrm{K} \cdot \mathrm{E}\) =0

⇒ \(-\frac{G M m}{2 R}+\frac{1}{2} m v^2\) =0

v =\(\sqrt{\frac{G M}{R^2}+R}=\sqrt{g R}\)

This confirms that:

fv =\(\frac{v}{\sqrt{2}}\)

f =\(\frac{1}{\sqrt{2}}\)

Question 49. Which velocity should a particle be projected so that its height becomes equal to the radius of Earth?

1. \(\left(\frac{G M}{R}\right)^{1 / 2}\)
2. \(\left(\frac{8 G M}{R}\right)^{1 / 2}\)
3. \(\left(\frac{2 G M}{R}\right)^{1 / 2}\)
4. \(\left(\frac{4 G M}{R}\right)^{1 / 2}\)

Answer: 1. \(\left(\frac{G M}{R}\right)^{1 / 2}\)

Use , \(v^2=\frac{2 g n}{1+\frac{h}{R}}\) given h= R

v=\(\sqrt{g R}=\sqrt{\frac{G M}{R}}\)

Question 50. For a planet having mass equal to the mass of the Earth the radius is one-fourth of the radius of the Earth. The escape velocity for this planet will be :

1. 11.2 km/s
2. 22.4 km/s
3. 5.6 km/s
4. 44.8 km/s

Answer: 2. 22.4 km/s

⇒ \(v_e =\sqrt{2 g R_e}=\sqrt{\frac{2 G M}{R_e}}\)

⇒ \(R_p =\frac{1}{4} R_e\)

∴ \(v_p =2 v_e=2 \times 11.2=22.4 \mathrm{~km} / \mathrm{s}\)

Question 51. The escape velocity of a sphere of mass m is given by (G = Universal gravitational constant; M_e = Mass of the earth and R_e = Radius of the earth)₁

1. \(\sqrt{\frac{2 G M_e m}{R_e}}\)
2. \(\sqrt{\frac{2 G M_e}{R_e}}\)
3. \(\sqrt{\frac{G M_e}{R_e}}\)
4. \(\sqrt{\frac{2 G M_e+R_e}{R_e}}\)

Answer: 2. \(\sqrt{\frac{2 G M_e}{R_e}}\)

To escape Earth’s gravitational pull and reach infinity, the starting kinetic energy must be somewhat more than the gravitational potential energy of the body on the surface.

The total energy of the body just after projecting is: \(\mathrm{E}=\frac{1}{2} m v^2-\frac{G M_e m}{R_e}\)

This total energy must now be slightly greater than zero for the minimum speed to be achieved when kinetic energy equals gravitational potential energy.

⇒ \(\frac{1}{2} m v^2 =\frac{G M_e m}{R_e}\)

⇒ \(\frac{1}{2} v^2 =\frac{G M_e}{R_e}\)

v =\(\sqrt{\frac{2 G M_e}{R_e}}\)

Question 52. The escape velocity of a body on the surface of the Earth is 11.2 km/s. If the Earth’s mass increases to twice its present value and the radius of the Earth becomes half, the escape velocity becomes:

1. 22.4 km/s
2. 44.8 km/s
3. 5.6 km/s
4. 11.2 km/s

Answer: 1. 22.4 km/s

Escape velocity of a body \(\left(v_e\right)=11.2 \mathrm{~km} / \mathrm{s}\);

New mass of the Earth \(M_e^{\prime}=2 M_e \) and the new radius of the Earth \(R_e^{\prime}=0.5 R_e\)

Escape velocity \(\left(v_e\right)=\sqrt{\frac{2 G M_e}{R_e}} \propto \sqrt{\frac{M_e}{R_e}}\)

⇒ \(\frac{v_e}{v_e^{\prime}} =\sqrt{\frac{M_e}{R_e} \times \frac{0.5 R_e}{2 M_e}}\)=\(\sqrt{\frac{1}{4}}=\frac{1}{2}\)

∴ \(v_e^{\prime} =2 v_e=22.4 \mathrm{~km} / \mathrm{s}\)

Question 53. The escape velocity from the Earth is 11.2 km/s. If a body is to be projected in a direction making an angle of 45° to the vertical, then the escape velocity is :

1. 11.2×2 km/s
2. 11.2 km/s
3. \(\frac{11.2}{\sqrt{2}} \mathrm{~km} / \mathrm{s}\)
4. \(11.2 \sqrt{2} \mathrm{~km} / \mathrm{s}\)

Answer: 2. 11.2 km/s

As, \(v_e=\sqrt{2 g R}=\sqrt{\frac{2 G M}{R}}\)

Hence, escape velocity does not depend on the angle of projection. Escape velocity will remain the same.

Hence, the escape velocity is 11.2 Km/s.

Question 54. For a satellite escape velocity is 11 km/s. If the satellite is launched at an angle of 60° with the vertical, then the escape velocity will be

1. \(11 \mathrm{~km} / \mathrm{s}\)
2. \(11 \sqrt{3} \mathrm{~km} / \mathrm{s}\)
3. \(\frac{11}{\sqrt{3}} \mathrm{~km} / \mathrm{s}\)
4. \(33 \mathrm{~km} / \mathrm{s}\)

Answer: 3. \(\frac{11}{\sqrt{3}} \mathrm{~km} / \mathrm{s}\)

Escape velocity on Earth is the minimum velocity with which the body has to be projected vertically upwards from the surface of the Earth. So, that it just crosses the gravitational field of Earth and never returns on its own. The escape velocity of the Earth is given by

⇒ \(v_e =\sqrt{\frac{2 G M}{R}}=\sqrt{2 g R}\)

=\(\sqrt{\frac{8 \pi \rho G R^2}{3}}\)

It is clear from the above equation that the value of a body’s escape velocity is independent of its mass (m) and angle of projection from the planet’s surface. As a result, the escape velocity remains unchanged. Hence, v = 11 km/s Projected velocity.

Question 55. The escape velocity from the Earth’s surface is v. The escape velocity from the surface of another planet having a radius, four times that of Earth and the same mass density is:

1. v
2. 2v
3. 3v
4. 4v

Answer: 2. 2v

Given the escape velocity of Earth = v

Radius of other planet = \(4 \mathrm{R}_e\)

Mass density is same = d

Mass of other planet =\(\frac{4}{3} \pi\left(4 \mathrm{R}_{\mathrm{e}}\right)^3 \cdot d \)

Mass of Earth =\(\frac{4}{3} \pi \mathrm{R}_{\mathrm{e}}^3 \cdot d \)

⇒ \(\mathrm{M}=\frac{\mathrm{M}_{\mathrm{P}}}{\mathrm{M}_e}=\frac{64 \mathrm{R}_e^3}{\mathrm{R}_e^3}\)=64

⇒ \(\mathrm{M}_P=64 \mathrm{M}_{\mathrm{e}}\)

We know, \(v_e=\sqrt{\frac{2 \mathrm{GM}_e}{\mathrm{R}_e}}\)

⇒ \(v_P=\sqrt{\frac{2 \mathrm{G}\left(64 \mathrm{M}_e\right)}{4 \mathrm{R}_e}}\)

=\(4 \sqrt{\frac{2 \mathrm{GM}_e}{\mathrm{R}_e}}\)

⇒ \(\frac{v_P}{v_e}\)=4

∴ \(v_P=4 v_e \)

Question 56. The period of a geostationary satellite is 24 h, at a height of 6RE (R_E is the radius of Earth) from the surface of Earth. The period of another satellite whose height is 2.5 R_E from the surface will be:

1. \(6 \sqrt{2} h\)
2. \(12 \sqrt{2} h\)
3. \(\frac{24}{2.5} h\)
4. \(\frac{12}{2.5} h\)

Answer: 1. \(6 \sqrt{2} h\)

From Kepler’s third law we know that period:

⇒ \(\mathrm{T}^2 \propto r^3\)

⇒ \(\mathrm{~T} =\sqrt[2]{r^3}\)  →  Equation 1

Where, r= radius of satellite’s orbit

Now from question, \(r_1=6 \mathrm{R}_{\mathrm{E}}+\mathrm{R}_{\mathrm{E}}, \mathrm{T}_1=24 \mathrm{~h}\)

⇒ \(r_2=2.5 \mathrm{R}_{\mathrm{E}}+\mathrm{R}_{\mathrm{E}}, \mathrm{T}_2\)=?

From eq. (1) we can write,

⇒ \(\left(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right)=\left(\frac{r_1}{r_2}\right)^{3 / 2}\)

Putting the given values,

⇒ \(\frac{24}{\mathrm{~T}_2} =\left(\frac{6 \mathrm{R}_{\mathrm{E}} 7 \mathrm{R}_{\mathrm{E}}}{2.5 \mathrm{R}_{\mathrm{E}} 7 \mathrm{R}_{\mathrm{E}}}\right)^{3 / 2}=\left(\frac{7 \mathrm{R}_{\mathrm{E}}}{3.5 \mathrm{R}_{\mathrm{E}}}\right)^{3 / 2}\)

=\(\left(\frac{7}{3.5}\right)^{3 / 2}=(2)^{3 / 2}\)

⇒ \(\mathrm{T}_2 =\frac{24}{(2)^{3 / 2}}\)

=\(\frac{24}{2 \sqrt{2}}=6 \sqrt{2} h\)

Question 57. A remote sensing satellite of Earth revolves in a circular orbit at a height of 0.25 x 10⁶ m above the surface of Earth. If Earth’s radius is 6.38 x 10⁶ m and g = 9.8 ms^-2, then the orbital speed of the satellite is:

1. 7.76 km^-1
2. 8.56 km^-1
3. 9.13 km^-1
4. 6.67 km^-1

Answer: 1. 7.76 km^-1

According to question, Height of a satellite, h=\(0.25 \times 10^6 \mathrm{~m}\)

Radius of Earth, \(R_E=6.38 \times 10^6 \mathrm{~m}\)

For the satellite revolving around the Earth

⇒ \(v_0=\sqrt{\frac{G M_E}{R_E}}=\sqrt{\frac{G M_E}{R_E\left[1+\frac{h}{R_E}\right]}}\)

=\(\sqrt{\frac{g R_E}{1+\frac{h}{R_E}}}\)

Putting value, \(v_0 =\sqrt{\frac{9.8 \times 6.38 \times 10^6}{1+\frac{0.25 \times 10^6}{6.38 \times 10^6}}}=\sqrt{60 \times 10^6}\)

=\(7.76 \times 10^3 \mathrm{~ms}^{-1}=7.76 \mathrm{~km} / \mathrm{s}\)

Question 58. A satellite S is moving in an elliptical orbit around the Earth. The mass of the satellite is very small compared to the mass of the Earth. Then:

1. the angular momentum of S about the centre of the Earth changes in direction, but its magnitude remains constant
2. the total mechanical energy of S varies periodically with time
3. the linear momentum of S remains constant in magnitude
4. the acceleration of S is always directed towards the centre of the Earth

Answer: 4. the acceleration of S is always directed towards the centre of the Earth

The mass of satellites is very small. The Centre of mass of the system coincides with the centre of the Earth

Question 59. A geostationary satellite is orbiting the Earth at a height of 5R above the surface of the Earth, R being the radius of the Earth. The period of another satellite in hours at a height of 2R from the surface of the Earth is:

1. 5
2. 10
3. \(6 \sqrt{2}\)
4. \(\frac{6}{\sqrt{2}}\)

Answer: 3. \(6 \sqrt{2}\)

Using Kepler’s third law as \(\mathrm{T}^2 \propto r^3\)

⇒ \(T_1^2 \propto r_1^3 \) and \( T_2^2 \propto r_2^3\)

⇒ \(\frac{T_2^2}{T_1^2}=\frac{r_2^3}{r_1^3}=\frac{(3 R)^3}{(6 R)^3}=\frac{1}{8}\)

⇒ \(T_2^2=\frac{1}{8} T_1^2\)

∴ \(T_S=\frac{24}{2 \sqrt{2}}=6 \sqrt{2} h\)

Question 60. If \(v_e\) is escaping velocity and \(v_0\) is the orbital velocity of a satellite for orbit close to Each surface, then these are related by:

1. \(v_0=\sqrt{2} v_e\)
2. \(v_0=v_e\)
3. \(v_e=\sqrt{2} v_0\)
4. \(v_e=\sqrt{2} v_0\)

Answer: 3. \(v_e=\sqrt{2} v_0\)

From the question, \(v_{\text {escape }}=\sqrt{\frac{2 G M}{R}}=v_e\)

⇒ \(v_{\text {orbital }}=\sqrt{\frac{G M}{R}}=v_0\)

From the above equations,

∴ \(v_e=\sqrt{2} v_0\)

Question 61. The radii of the circular orbits of two satellites A and B of the Earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be:

1. 3v/4
2. 6 v
3. 12v
4. 3v/2

Answer: 2. 6 v

According to the question,

Radius of satellite A = 4R

and radius of satellite B = R

Speed of satellite A = 3v

Speed of satellite B =?

We know that orbital velocity of satellite is, v =\(\sqrt{\frac{G M}{r}}\)

⇒ \(\frac{v_A}{v_B} =\sqrt{\frac{r_{\mathrm{B}}}{r_{\mathrm{A}}}}\)

=\(\sqrt{\frac{R}{4 R}}=\frac{1}{2}=\frac{3 v}{v_B}\)

∴ \(v_B =6 v\)

Question 62. A ball is dropped from a spacecraft revolving around the Earth at a height of 120 km. What will happen to the ball?

1. it will fall to the Earth gradually
2. it will go very far in the space
3. it will continue to move with the same speed along the original orbit of the spacecraft
4. it will move with the same speed, tangentially to the spacecraft

Answer: 3. it will continue to move with the same speed along the original orbit of the spacecraft

Since no external torque is applied therefore according to the law of conservation of angular momentum, the ball will continue to move with the same angular velocity along the original orbit of the spacecraft.

Question 63. The escape velocity from the surface of the Earth is \(v_e\). The escape velocity from the surface of a planet whose mass and radius are three times those of the Earth will be:

1. \(v_e\)
2. \(3 v_e\)
3. \(9 v_e\)
4. \(\frac{1}{3 v_{\mathrm{e}}}\)

Answer: 1. \(v_e\)

Escape velocity on the surface of the Earth is given by

⇒ \(v_e =\sqrt{2 g R_{\mathrm{e}}}\)

=\(\sqrt{\frac{2 G M_{\mathrm{e}}}{R_{\mathrm{e}}}}  g=\frac{G M_{\mathrm{e}}}{R_e^2}\)

where, \(M_e\)= mass of Earth

⇒\(R_{\mathrm{e}}\)= radius of the Earth

G= gravitational constant

⇒ \(v_{\mathrm{e}} \propto \sqrt{\frac{M_{\mathrm{e}}}{R_{\mathrm{e}}}}\)

If \(v_p\) is escape velocity from the surface of the planet, then,

⇒ \(\frac{v_e}{v_p}=\sqrt{\frac{M_e}{R_e}} \times \sqrt{\frac{R_P}{M_P}}\)

where, \(M_p\) is mass of the planet and \(R_p\) is radius of the planet.

but \(R_p=3 R_e\) { (given) }

and \(M_p=3 M_e\)

⇒ \(\frac{v_e}{v_p} =\sqrt{\frac{M_e}{R_e}} \times \sqrt{\frac{3 R_e}{3 M_e}}\)

=\(\frac{1}{1}\)

or \(v_p=v_e\)

Question 64. A satellite I of mass m is at a distance r from the surface of the Earth. Another satellite B of mass 2 z is at a distance of 2 r from the Earth’s surface. Their periods are in the ratio of

1. 1:2
2. 1:16
3. 1:32
4. \(1: 2 \sqrt{2}\)

Answer: 4. \(1: 2 \sqrt{2}\)

According to Kepler’s third law, the square of the period of revolution of a planet around the sun is directly proportional to the cube of the major- axis of its elliptical orbit i.e. \( T^2 \alpha r^3\)

where T= time taken by the planet to go once around the sun.

r= semi-major axis of the elliptical orbit

⇒ \(\frac{T_1^2}{T_2^2}=\frac{(r)^3}{(2 r)^3}=\frac{1}{8}\)

∴ \(\frac{T_1}{T_2}=\frac{1}{2 \sqrt{2}}\)

Question 65. The additional kinetic energy to be provided to a satellite of mass ia revolving around a planet of mass M, to transfer it from a circular orbit of radius \(R_1\) to another of radius \(R_2\left(R_2>R_1\right)\) is:

1. \(G m M\left(\frac{1}{R_1^2}-\frac{1}{R_2^2}\right)\)
2. \(G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
3. \(2 G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
4. \(\frac{1}{2} G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

Answer: 4. \(\frac{1}{2} G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

The kinetic energy of the orbit of the satellite,

K E =\(\frac{\mathrm{GM} m}{2 \mathrm{R}_1}+\left(-\frac{\mathrm{GMm}}{2 \mathrm{R}_2}\right)\)

=\(\frac{\mathrm{GM} m}{2}\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right]\)

Question 66. Assuming that the gravitational potential energy of an object at infinity is zero, the change in potential energy (final-initial) of an object of mass ru when taken to a height ft from the surface of Earth (of radius R) is given by:

1. \(\frac{G M m}{R+h}\)
2. \(\frac{G M m h}{R(R+h)}\)
3. mg
4. \(\frac{G M m}{R+h}\)

Answer: 2. \(\frac{G M m h}{R(R+h)}\)

⇒ \({ P.E. })_{\mathrm{A}} =-\frac{G M m}{R}\)

⇒ \({ P.E. })_{\mathrm{B}} =-\frac{G M m}{R+h}\)

⇒ \(\Delta U =(\mathrm{P} . \mathrm{E})_{\mathrm{B}}-(\mathrm{P} . \mathrm{E})_{\mathrm{A}}\)

=\(\frac{G M m}{R+h}+\frac{G M m}{R}\)

=\(\frac{G M m h}{R(R+h)}\)

Question 67. A satellite of mass z is orbiting the Earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of g₀, the value of acceleration due to gravity at the Earth’s surface is:

1. \(\frac{m g_0 \mathrm{R}^2}{2(\mathrm{R}+h)}\)
2. \(-\frac{m g_0 \mathrm{R}^2}{2(\mathrm{R}+h)}\)
3. \(\frac{2 m g_0 \mathrm{R}^2}{\mathrm{R}+h}\)
4. \(-\frac{2 m g_0 \mathrm{R}^2}{\mathrm{R}+h}\)

Answer: 2. \(-\frac{m g_0 \mathrm{R}^2}{2(\mathrm{R}+h)}\)

Total energy =K.E +P.K.

=\(\frac{G M m}{2(R+h)}-\frac{G M m}{(R+h)}\)

=\(\frac{-G M m}{2(R+h)}-\frac{G M m}{(R+h)}\)

=\(\frac{-m g^{\prime} R^2}{2(R+h)}\)

∴ \(\left(\text { where, } g^{\prime}\right.\left.=\frac{G M}{R^2}\right)\)

Question 68. Two satellites of Earth, S₁ and S₂ are moving in the same orbit. The mass of S₁ of four times the mass of S₂. Which one of the following statements is true?

1. The potential energies of Earth and satellite in the two cases are equal.
2. S₁ and S₂ are moving at the same speed
3. The kinetic energies of the two satellites are equal
4. The period of S₁ is four times that of S₂.

Answer: 2. S₁ and S₂ are moving at the same speed

⇒ \({K.E.}=\frac{G M m}{2 r}\)

Kinetic energies are unequal,

⇒ \(\mathrm{T}=\frac{2 \pi r^{3 / 2}}{\sqrt{G M}}\)

Periods are equal,

⇒ \({ P.E. }=-\frac{G M m}{r}\)

Potential energies are unequal,

V=\(\sqrt{\frac{G M}{r}}\)

orbital speeds are equal.

Question 69. For a satellite in an orbit around the Earth, the ratio of kinetic, energy to potential energy is:

1. \(\frac{1}{2}\)
2. \(\frac{1}{\sqrt{2}}\)
3. 2
4. \(\sqrt{2}\)

Answer: 1. \(\frac{1}{2}\)

⇒ \(-\frac{\mathrm{GMm}}{R^2}+m \omega^2 R \)=0

⇒ \(\frac{\mathrm{GMm}}{R^2} =m \omega^2 R\)

K.E. \( =\frac{1}{2} I \omega^2\)

=\(\frac{1}{2} m R^2 \omega^2\)

=\(\frac{\mathrm{GMm}}{2 R}\)

P.E =\(-\frac{\mathrm{GMm}}{R}\)

K.E =\(\frac{|P \cdot E|}{2}\)

∴ \(\frac{K . E}{P. E} =\frac{1}{2}\)

Question 70. The satellite of mass m is orbiting around the Earth in a circular orbit with a velocity v. What will be its total energy?

1. \((3 / 4) m v^2\)
2. \((1 / 2) m v^2\)
3. \(m v^2\)
4. \(-(1 / 2) m v^2\)

Answer: 4. \(-(1 / 2) m v^2\)

⇒ \({ K.E. of sattelite }=\frac{1}{2} m v^2\)

⇒ \({ (where, } v=\sqrt{\frac{G M}{r^2}}\)

P.E. of sattelite =\(\frac{G M m}{r}=-m v^2 \)

Total Energy = K. E. + P. E.

=\(\frac{1}{2} m v^2-m v^2=-\frac{1}{2} m v^2\)

Question 71. The mean radius of Earth is R, its angular speed on its axis is o and the acceleration due to gravity at Earth’s surface is g. What will be the radius of the orbit of a geostationary satellite?

1. \(\left(R^2 g / \omega^2\right)^{1 / 3}\)
2. \(\left(R g / \omega^2\right)^{1 / 3}\)
3. \(\left(R^2 \omega^2 / g\right)^{1 / 3}\)
4. \(\left(R^2 g / \omega\right)^{1 / 3}\)

Answer: 1. \(\left(R^2 g / \omega^2\right)^{1 / 3}\)

⇒ \(\frac{G M m}{r^2} =m \omega^2 r\)

r =\(\left(g R^2 / \omega^2\right)^{1 / 3}\)

NEET Physics For System Of Particles And Rotational Motion Multiple Choice Questions

Question 1. Three identical spheres, each of mass M, are placed at the comers of a right-angled triangle with mutually perpendicular sides equal to 2 m (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, the position vector of the centre of mass is

1. \(2(\hat{i}+\hat{j})\)
2. \((\hat{i}+\hat{j})\)
3. \(\frac{2}{3}(\hat{i}+\hat{j})\)
4. \(\frac{4}{3}(\hat{i}+\hat{j})\)

Answer: 2. \((\hat{i}+\hat{j})\)

See The Figure,

Given

Three identical spheres, each of mass M, are placed at the comers of a right-angled triangle with mutually perpendicular sides equal to 2 m (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin,

⇒ \(\mathrm{OA}=2 \hat{i}\)

⇒ \(\mathrm{OB}=2 \hat{j}\)

Position vector of centre of mass, \(\mathrm{R}_{\mathrm{CM}} =\frac{m_1 r_1+m_2 r_2}{m_1+m_2}\)

=\(\frac{M \cdot \mathrm{OA}+M \cdot \mathrm{OB}}{M+M}\)

=\(\frac{M \times 2 \hat{i}+M \times 2 \hat{j}}{2 M}=\hat{i}+\hat{j}\)

Question 2. Two particles of mass 5 kg and 10 kg respectively are attached to the two ends of a rigid rod of length 1 m with negligible mass. The centre of mass of the system from the 5 kg particle is nearly at a distance of:

1. 50 cm
2. 67 cm
3. 80 cm
4. 33 cm

Answer: 2. 67 cm

Given That,

Two particles of mass 5 kg and 10 kg respectively are attached to the two ends of a rigid rod of length 1 m with negligible mass.

⇒ \(\frac{m_1 r_1-m_2 r_2}{m_1+m_2}\) =0

⇒ \(5 r_1-10 r_2\) =0

⇒ \(r_2 =\frac{r_1}{2}\)

⇒ \(r_1+r_2\) =100

⇒ \(r_1+\frac{r_1}{2}\) =100

⇒ \(3 r_1\) =200

∴ \(r_1 =\frac{200}{3}=67 \mathrm{~cm}\)

Read and Learn More NEET Physics MCQs

Question 3. Three masses are placed on the x-axis: 300 g at origin, 500 g at x = 40 cm and 400 g at x = 70 cm. The distance of the centre of mass of the origin is:

1. 40 cm
2. 45 cm
3. 50 cm
4. 30 cm

Answer: 1. 40 cm

⇒ Centre of mass\(r_{\mathrm{cm}} =\frac{m_1 x_1+m_2 x_2+m_3 x_3}{m_1+m_2+m_3}\)

=\(\frac{300 \times 0+500 \times 40+400 \times 70}{300+500+400}\)

=40 cm

Question 4. Two bodies of mass 1 kg and 3 kg have position vectors \(\hat{i}+2 \hat{j}+\hat{k}\) and \(-3 \hat{i}+2 \hat{j}+\hat{k}\) respectively. The centre of mass of this system has a position vector:

1. \(-2 \hat{i}+2 \hat{k}\)
2. \(-2 \hat{i}-\hat{j}+\hat{k}\)
3. \(2 \hat{i}-\hat{j}-2 \hat{k}\)
4. \(-\hat{i}-\hat{j}+\hat{k}\)

Answer: 2. \(-2 \hat{i}-\hat{j}+\hat{k}\)

According to the question,

Position Vector\(\vec{r} =\frac{m_1 \vec{r}_1+m_2 \vec{r}_2}{m_1+m_2}\)

⇒ \(\vec{r} =\frac{1(\hat{i}+2 \hat{j}+k)+3(-3 \hat{i}-2 \hat{j}+\hat{k})}{1+3}\)

⇒ \(\vec{r} =\frac{1}{4}(-8 \hat{i}-2 \hat{j}+4 \hat{k})\)

⇒ \(\vec{r} =-2 \hat{i}-2 \hat{j}+\hat{k}\)

Question 5. A uniform rod of length l and mass m is free to rotate in a vertical plane about A. The rod initially in a horizontal position is released. The initial angular acceleration of the rod is (moment of inertia of the rod about A is \(\frac{m l^2}{3}\):

1. \(m g \frac{l}{2}\)
2. \(\frac{3 g}{2 l}\)
3. \(\frac{2 l}{3 g}\)
4. \(\frac{3 g}{2 l^2}\)

Answer: 2. \(\frac{3 g}{2 l}\)

Here torque,

The moment of Inertia of the rod about A is:

I=\(\frac{m l^2}{3}\)

Angular acceleration of the rod is \(\alpha=\frac{\tau}{I}\)

∴ \(\alpha=\frac{m g\left(\frac{1}{2}\right)}{\frac{m l^2}{3}}=\frac{3 g}{2 l}\)

Question 6. Consider a system of two particles having masses m₁ and m₂. If the particle of mass m₁ is pushed towards the mass centre of a particle through a distance d, by what distance would the particle of mass m₂ move to keep the mass centre of particles at the original position?

1. \(\frac{m_1}{m_1+m_2} d\)
2. \(\frac{m_1}{m_2} d\)
3. \(\frac{d\left(m_1+m_2\right)}{m_1}\)
4. \(\frac{m_2}{m_1}\)

Answer: 2. \(\frac{m_1}{m_2} d\)

We know that, \(\mathrm{CM}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)

After changing the position of m₁ and keeping the position of C.M. the same.

C.M. =\(\frac{m_1\left(x_1 d\right)+m_2\left(\mathrm{x}_2-d_2\right)}{m_1+m_2}\)

0 =\(\frac{m_1 d-m_2 d_2}{m_1+m_2}\)

⇒ \(d_2  =\frac{m_1}{m_2} d\)

∴ C.M. =\(\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)

Question 7. Consider a system of two particles having masses m₁ and m₂. If the particle of mass m1 is pushed towards the centre of mass of the particles through a distance d, by what distance would be particle of mass m₂ move to keep the centre of mass of the particles at the original position?

1. \(\frac{m_1}{m_1+m_2} d\)
2. \(\frac{m_1}{m_2} d\)
3. d
4. \(\frac{m_2}{m_1} d\)

Answer: 2. \(\frac{m_1}{m_2} d\)

After changing the position of m₁ and keeping the position of C.M. same

C.M.=\(\frac{m_1\left(x_1-d\right)+m_2\left(x_2+d_2\right)}{m_1+m_2}\)

0 =\(\frac{-m_1 d+m_2 d_2}{m_1+m_2}\)

[Substituting value of C.M. from (1)

∴ \(d_2=\frac{m_1}{m_2} d\)

Question 8. Three identical metal balls, each of radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed when the centres of the three balls are joined. The centre of the mass of the system is located at:

1. line joining centres of my two balls
2. centre of one of the balls
3. horizontal surface
4. point of intersection of the medians

Answer: 4. point of intersection of the medians

Centre of mass of each ball lies on the centre

The Centre of mass of the combined body will be at the centroid of an equilateral triangle.

Question 9. Two objects of mass 10 kg and 20 kg respectively are connected to the two ends of a rigid rod of length 10 m with negligible mass. The distance of the centre of mass of the system from the 10 kg mass is :

1. \(\frac{20}{3} m\)
2. \(10 \mathrm{~m}\)
3. \(5 \mathrm{~m}\)
4. \(\frac{10}{3} m\)

Answer: 1. \(\frac{20}{3} m\)

Given, M₁ = 10kg, M₂ = 20kg,

Length of rod = 10 m

Let M₁ be at the origin, and then X₁ and X₂ are 0 and 10 m respectively.

Centre of mass, X=\(\frac{M_1 X_1+M_2 X_2}{M_1+M_2}\)

Putting the values in above equation we get, X=\(\frac{10 \times 0+20 \times 10}{10+20}=\frac{200}{30}=\frac{20}{3}\)

The distance of the centre of mass of the system from the 10 kg mass is: 20/3 m

Question 10. Two persons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat. The length of the boat is 3.0 m and weighs 100 kg. The 55 kg man walks up to the 65 kg man and sits with him. If the boat is in still water. The centre of mass of the system shifts by:

1. 3.0 m
2. 2.3 m
3. zero
4. 0.75 m

Answer: 3. zero

Since no external force is applied to the system. And centre of mass (CM) be at rest. So our answer is option (C) zero

Question 11. The resultant of \(\vec{A}\) x 0 will be equal to:

1. zero
2. A
3. zero vector
4. unit vector

Answer: 3. zero vector

∴ \(\vec{A} \times 0\) is a zero vector

Question 12. Vectors, \(\vec{A}, \vec{B} \text { and } \vec{C}\) are such that \(\vec{A} \cdot \vec{B}\) = 0 and \(\vec{A} \cdot \vec{C}\)= 0. Then the vector parallel to A is:

1. \(\vec{A} \times \vec{B}\)
2. \(\vec{B}+\vec{C}\)
3. \(\vec{B} \times \vec{C}\)
4. \(\vec{B}and \vec{C}\)

Answer: 3. \(\vec{B} \times \vec{C}\)

Vector triple product of three vectors \(\vec{A}, \vec{B}\) and \(\vec{C}\) is:

Given : \(\vec{A} \times(\vec{B} \times \vec{C})=(\vec{A} \cdot \vec{C}) \vec{B}-(\vec{A} \cdot \vec{B}) \vec{C}\)

⇒ \(\vec{A} \cdot \vec{B}=0, \vec{A} \cdot \vec{C}\)=0

⇒ \(\vec{A} \times(\vec{B} \times \vec{C})\)=0

∴ Thus the vector \(\vec{A}\) is parallel to vector \(\vec{B} \times \vec{C}\).

Question 13.\(\vec{A} \text { and } \vec{B}\) are two vectors and θ is the angle between them, if \(|\vec{A} \times \vec{B}|=\sqrt{3}(\vec{A} \cdot \vec{B})\), the value of θ is:

1. 45°
2. 30°
3. 90°
4. 60°

Answer: 4. 60°

⇒ \(|\vec{A} \times \vec{B}| \) = \(\sqrt{3}(\vec{A} \cdot \vec{B})\)

⇒ \(A B \sin \theta =\sqrt{3} A B \cos \theta\)

or \(\tan \theta =\sqrt{3}\)

or \(\theta =\tan ^{-1} \sqrt{3}=60^{\circ}\)

Question 14. If the angle between the vectors\(\vec{A} \text { and } \vec{B}\) is θ, the value of the product \((\vec{B} \times \vec{A}) \cdot \vec{A}\) A is equal to:

1. \(B A^2 \sin \theta\)
2. \(B A^2 \cos \theta\)
3. \(B A^2 \sin \theta \cos \theta\)
4. zero

Answer: 4. zero

Let, \(|\vec{A} \times \vec{B}|=\vec{C}\)

The cross product of ,\(\vec{B}\) and \(\vec{A}\) is perpendicular to the plane containing \(\vec{A} \)and \(\vec{B}\) i.e. perpendicular to \(\vec{A}\)

Therefore Product Of \((\vec{B} \times \vec{A}) \cdot \vec{A}\)=0

Question 15.If \(|\vec{A} \times \vec{B}|=\sqrt{3} \vec{A} \cdot \vec{B}\) then the value of \(|\vec{A}+\vec{B}|\) is:

1. \(\left(A^2+B^2+A B\right)^{1 / 2}\)
2. \(\left(A^2+B^2+\frac{A B}{\sqrt{3}}\right)^{1 / 2}\)
3. A+B
4. \(\left(A^2+B^2+\sqrt{3} A B\right)^{1 / 2}\)

Answer: 1. \(\left(A^2+B^2+A B\right)^{1 / 2}\)

⇒ \(|\vec{A} \times \vec{B}| =\sqrt{3} \vec{A} \cdot \vec{B}\)

⇒ \(|\vec{A} \| \vec{B}| \sin \theta =\sqrt{3}|\vec{A} \| \vec{B}| \cos \theta\)

⇒ \(\tan \theta =\sqrt{3}\)

⇒ \(\theta =60^{\circ}\)

⇒ \(|\vec{A}+\vec{B}| =\sqrt{|\vec{A}|^2+|\vec{B}|^2+2|\vec{A} \| \vec{B}| \cos \theta}\)

=\(\left(A^2+B^2+A B\right)^{1 / 2}\)

Question 16. A disc is rotating with angular velocity about its axis (without any translation push) on a smooth surface: Find the direction and magnitude of velocity at points B and A

1. \( -\omega {R} \) towards left
2. \(-\omega {R} \) towards right
3. \( +\omega {R} \) towards left
4. \( +\omega R \) towards left

Answer: 1. \( -\omega \mathrm{R} towards left \)

In the given question

Velocity at A, \( v_A=\omega\left(\frac{\mathrm{R}}{2}\right)\) towards right

∴ Velocity at B, \(v_B=-\omega\) R towards left

Question 17. What is the value of linear velocity, \(\vec{r}=3 \hat{i}-4 \hat{j}+\hat{k}\) and \(\vec{\omega}=5 \hat{i}-6 \hat{j}+6 \hat{k}\)?

1. \(4 \hat{i}-13 \hat{j}+6 \hat{k}\)
2. \(18 \hat{i}+13 \hat{j}-2 \hat{k}\)
3. \(6 \hat{i}+2 \hat{j}-3 \hat{k}\)
4. \(6 \hat{i}-2 \hat{j}+8 \hat{k}\)

Answer: 2. \(18 \hat{i}+13 \hat{j}-2 \hat{k}\)

Question 18. A uniform rod of length 200 cm and mass 500 g is balanced on a wedge placed at the 40 cm mark. A mass of 2 kg is suspended from the rod at 20 cm and another unknown mass ‘m’ is suspended from the rod at the 160 cm mark as shown in the figure. Find the value of ‘m’ such that the rod is in equilibrium, (g = 10 m/s²):

1. \(\frac{1}{2} \mathrm{~kg}\)
2. \(\frac{1}{3} \mathrm{~kg}\)
3. \(\frac{1}{6} \mathrm{~kg}\)
4. \(\frac{1}{12} \mathrm{~kg}\)

Answer: 4. \(\frac{1}{12} \mathrm{~kg}\)

Applying the principle of momentums, LHM = 2 x 20

RHM = 0.5 x 60 + m x 120

2 x 20=30+ 120m

10= 120m

∴ \(m=\frac{10}{120}=\frac{1}{12} \mathrm{~kg}\)

Question 19. Find the torque about the origin, when a force of 3\(\hat{\boldsymbol{j}}\)N acts on the particle whose position vector is \(\hat{k}\)

1. \(6 \hat{j} \mathrm{~N}-\mathrm{m}\)
2. \(-6 \hat{i} \mathrm{~N}-\mathrm{m}\)
3. \(-6 \hat{k} \mathrm{~N}-\mathrm{m}\)
4. \(6 \hat{i} \mathrm{~N}-\mathrm{m}\)

Answer: 2. \(-6 \hat{i} \mathrm{~N}-\mathrm{m}\)

According to question, Position vector \(\hat{r} =2 \hat{k} m\)

Force, \({\mathrm{F}} =3 \hat{j} \mathrm{~N}\)

Torque, \(\vec{\tau} =\vec{r} \times \overrightarrow{\mathrm{F}}=2 \hat{k} \times 3 \hat{j}\)

= \(-6 \hat{i}\)

= \(-6 \hat{i} \mathrm{~N}-\mathrm{m}\)

Question 20. A force F = \(\vec{F}=\alpha \hat{i}+3 \hat{j}+6 \hat{k}\) is acting at a point r = \(\vec{r}=2 \hat{i}-6 \hat{j}-12 \hat{k}\). The value of a for which angular momentum about the origin is conserved is:

1. – 1
2. 2
3. zero
4. 1

Answer: 1. – 1

From the question, Force, \(\vec{F} =\alpha \hat{i}+3 \hat{j}+6 \hat{k}\)

and Position, \(\vec{r}  =2 \hat{i}-6 \hat{j}-12 \hat{k}\)

Using the law of conservation of angular moments \(\tau\) =constant

Question 21. When a mass is rotating in a plane about a fixed point, its angular momentum is directed along :

1. a line perpendicular to the plane of rotation
2. the line at an angle of 45° to the plane of rotation
3. the radius
4. the tangent to the orbit

Answer: 1. a line perpendicular to the plane of rotation

The formula is L = m (r x v). This shows that when a mass is rotating in a plane about a fixed point, its angular momentum is directed along a line perpendicular to the plane of rotation

Question 22. A magnetic needle suspended parallel to a magnetic field requires \(\sqrt{3} \mathrm{~J}\) J of work to turn it through 60°. The torque needed to maintain the needle in the position will be:

1. \(2 \sqrt{3} \mathrm{~J}\)
2. \(3 \mathrm{~J}\)
3. \(\sqrt{3} \mathrm{~J}\)
4. \(\frac{3}{2} \mathrm{~J}\)

Answer: 2. \(3 \mathrm{~J}\)

Work done, W = \(M B \left(\cos \theta_1-\cos \theta_2\right)\)

⇒ \(\sqrt{3} =M B\left(\cos 0^{\circ}-\cos 60^{\circ}\right)\)

⇒ \(\sqrt{3}  =\frac{M B}{2}\)

And Torque, \(\tau =M B \sin \theta\)

⇒ \(\tau =M B \sin 60^{\circ}=\sqrt{3} \frac{M B}{2}\)

From Equations 1 And 2

∴ \(\tau=(\sqrt{3})(\sqrt{3})=3 \mathrm{~J}\)

Question 23. If \(\vec{F}\) is the force acting on a particle having position  vector \(\vec{r} \text { and } \vec{\tau}\) be the torque of this force about the origin, then:

1. \(\vec{r} \cdot \vec{\tau} \neq 0\) and \(\vec{F} \cdot \vec{\tau}\)=0
2. \(\vec{r} \cdot \vec{\tau}>0\) and \(\vec{F} \cdot \vec{\tau}<0\)
3. \(\vec{r} \cdot \vec{\tau}=0\) and \(\vec{F} \cdot \vec{\tau}\)=0
4. \(\vec{r} \cdot \vec{\tau}=0\) and \(\vec{F} \cdot \vec{\tau} \neq 0\)

Answer: 3. \(\vec{r} \cdot \vec{\tau}=0\) and \(\vec{F} \cdot \vec{\tau}\)=0

Torque is an axial vector i.e., its direction is always perpendicular to the plane containing vectors \(\vec{r}\) and \(\vec{F}\).

Therefore, \(\vec{\tau}=\vec{r} \times \vec{F}\)

Torque is perpendicular to both \(\vec{r}\) and \(\vec{F}\).

⇒ \(\vec{\tau} \cdot \vec{r}\)=0

∴ \(\vec{F} \cdot \vec{r}\)=0

Question 24. A particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle concerning origin O is L_A, when it is at A and L_B when it is at B, then:

1. L_A = L_B
2. the relationship between L_A and L_B depends upon the slope of the line AB
3. L_A<L_B
4. L_A>L_B

Answer: 1. L_A = L_B

The moment of Momentum is angular momentum. OP is the same whether the mass is at A or B

⇒ \(L_A=L_B\)

Question 25. Which of the following statements is correct?

1. The centre of mass of a body always coincides with the centre of gravity of the body.

2. The centre of mass of a body is the point at which the total gravitational torque of the body is zero.

3. A couple on a body produces both translation and rotational motion in a body.

4. Mechanical advantage greater than one means that a small effort can be used to lift a large load.

1. (2) and (4)
2. (1) and (2)
3. (2) and (3)
4. (3) and (4)

Answer: 1. (2) and (4)

The Centre of mass may or may not coincide with the centre of gravity.

Question 26. A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is:

1. \(\frac{w x}{d}\)
2. \(\frac{w d}{x}\)
3. \(\frac{w(d-x)}{x}\)
4. \(\frac{w(d-x)}{d}\)

Answer: 4. \(\frac{w(d-x)}{d}\)

So, W=\(N_1+N_2\)  →  Equation  1

For equilibrium, \(N_1 x=N_2(d-\boldsymbol{x})\)

From 1 \(N_1 x =\left(W-N_1\right)(d-x)\)

⇒ \(N_1 x =W_d-W_x-N_1 d+N_1 x\)

⇒ \(N_1 d =W(d-x)\)

∴ \(N_1 =\frac{W(d-x)}{d}\)

Question 27. ABC is an equilateral triangle with O as its centre. F₁, F₂ and F₃ represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of FT is:

1. \(F_1+F_2\)
2. \(F_1-F_2\)
3. \(\frac{F_1+F_2}{2}\)
4. \(2\left(F_1+F_2\right)\)

Answer: 1. \(F_1+F_2\)

Using Torque, \(\tau=F r\)

Clockwise torque, \(\tau =\tau F_1+\tau F_2+\tau F_3\)

0 =\(F_1 r+F_2 r+F_3 r\)

∴ \(F_3  =F_1+F_2\)

Question 28.

1. The centre of gravity (CG) of a body is the point at which the weight of the body acts.
2. The centre of mass coincides with the centre of gravity if the earth is assumed to have an infinitely large radius.
3. To evaluate the gravitational field intensity due to anybody at an external point, the entire mass of the body can be considered to be concentrated at its CG.
4. The radius of gyration of anybody rotating about an axis is the length of the perpendicular dropped from the CG of the body to the axis.

Which one of the following pairs of statements is correct?

1. (4) and (1)
2. (1) and (2)
3. (2) and (3)
4. (3) and (4)

Answer: 1. (4) and (1)

The CG of a body is the point at which the weight of the body acts.

The radius of gyration of anybody rotating about an axis is the length of the perpendicular dropped from the CG of the body to the axis

Question 29. The ratio of the radius of gyration of a thin uniform disc about an axis passing through its centre and normal to its plane to the radius of gyration of the die about its diameter is ;

1. \(\sqrt{2}: 1\)
2. 4: 1
3. \(1: \sqrt{2}\)
4. 2:1

Answer: 1. \(\sqrt{2}: 1\)

The figure of a thin uniform disc and disc is shown below :

The radius of gyration of a thin uniform disc, k=\(\sqrt{\frac{I}{m}}\)  →   Equation  1

and moment of inertia of the disc, I=\(\frac{m R^2}{4}\)

Here we have R as the radius, and m as the mass Now, on putting the value in equation (1) we have The radius of gyration of the uniform disc;

⇒ \(k_1=\sqrt{\frac{\frac{m R^2}{2}}{m}}\)

⇒ \(k_1=\sqrt{\frac{R^2}{2}}\)  →   Equation  2

and the radius of gyration of the uniform disc;

⇒ \(k_2=\sqrt{\frac{m R^2}{4}}\)

⇒ \(k_2=\sqrt{\frac{R^2}{4}}\)  →  Equation  3

Now, on dividing equation (2) by equation (3) we have;

⇒ \(\frac{k_1}{k_2}  =\frac{\sqrt{\frac{R^2}{2}}}{\sqrt{\frac{R^2}{4}}}\)

∴ \(k_1: k_2 =\sqrt{2}: 1\)

Question 30. From a circular ring of mass ‘M’ and radius ‘R’, an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR₂’. Then the value of  K is:

1. \(\frac{3}{4}\)
2. \(\frac{7}{8}\)
3. \(\frac{1}{4}\)
4. \(\frac{1}{8}\)

Answer: 1. \(\frac{3}{4}\)

Given,

Mass = M

Radius = R

⇒ \(\text { arc } \theta  =90^{\circ}\)

⇒ \(\mathrm{I}_{\text {remaining }} =\mathrm{KMR}^2\)

⇒ \(\mathrm{~K}\) =?

⇒ \(\mathrm{I}  =r^2 \int d m\)

⇒ \(\frac{d m}{d r} =\frac{\mathrm{M}}{2 \pi \mathrm{R}} d r \)

d m =\(\frac{\mathrm{M}}{2 \pi \mathrm{R}} d r\)

⇒ \(\mathrm{I} =r^2 \int_0^{\frac{3}{2} \pi \mathrm{R}} \frac{M}{2 \pi \mathrm{R}} d r\)

⇒ \(\mathrm{I} =\frac{\mathrm{MR}^2}{2 \pi \mathrm{R}} \cdot \frac{3}{2} \pi \mathrm{R}\)

=\(\frac{3}{4} \mathrm{MR}^2\)

∴ \(\mathrm{~K} =\frac{3}{4}\)

Question 31. A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation (E_sphere/E_Cylinder) will be:

1. 2 : 3
2. 1: 5
3. 1: 4
4. 3: 1

Answer: 2. 1: 5

Given

A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and radius is also rotating about its geometrical axis with an angular speed twice that of the sphere.

We know That,KE=\(\frac{1}{2} I \omega^2\)

KE of sphere,\(K_S =\frac{1}{2} I_s \omega^2\)  Equation  1

= \(\frac{1}{2} \times \frac{2}{5} M R^2 \times \omega^2\)

In KE of cylinder,\(\mathrm{K}_{\mathrm{C}} =\frac{1}{2} I_e \omega^2\)   Equation  2

= \(\frac{1}{2} \times \frac{M R^2}{2} \times 4 \omega^2 \).

From (1) and (2),

∴ \(\frac{K_S}{K_C}=\frac{1}{5}\)

Question 32. A light rod of length / has two masses m₁ and m₂ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is:

1. \(\frac{m_1 m_2}{m_1+m_2} l^2\)
2. \(\frac{m_1+m_2}{m_1 m_2} l^2\)
3. \(\left(m_1+m_2\right)^2\)
4. \(\sqrt{m_1 m_2 l^2}\)

Answer: 1. \(\frac{m_1 m_2}{m_1+m_2} l^2\)

centre of mass of \(m_1 and m_2\) lies at

r =\(\frac{m_1 r_1+m_2 r_2}{m_1+m_2}\)

⇒ \(r_1 =\frac{m_2 l}{m_1+m_2}, r_2=\frac{m_1 l}{m_1+m_2}\)

=\(m_1\left[\frac{m_2 l}{m_1+m_2}\right]^2+m_2\left[\frac{m_1 l}{m_1+m_2}\right]^2\)

=\(\frac{m_1 m_2 l^2}{\left(m_1+m_2\right)^2}\left(m_1+m_2\right)\)

=\(\frac{m_1 m_2 l^2}{m_1+m_2}\)

Question 33. Two spherical bodies of masses M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body before the collision is:

1. 2.5 R
2. 4.5 R
3. 7.5/2
4. 1.5 R

Answer: 3. 7.5/2

Given

Two spherical bodies of masses M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only,

Mass of one spherical body = M its radii = R

Mass of second body = 5M,

Its radii = 2R

Then we have, M x =5 M(9 R-x)

x =45 R-5 x

x =\(\frac{45 R}{6}=7.5 \mathrm{R}\)

Question 34. From a circular disc of radius R and mass 9m, a small disc of mass M and radius \(\frac{R}{3}\)is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is:

1. \(\frac{40}{9} M R^2\)
2. \(M R^2\)
3. \(4 M R^2\)
4. \(\frac{4}{9} M R^2\)

Answer: 1. \(\frac{40}{9} M R^2\)

The Moment of Inertia of a disc about an axis perpendicular to the plane and passing through the centre,

I=\(I_1-I_2 \)

I=\(\frac{9 M R^2}{2}-\frac{M R^2}{18}\)

I=\(\frac{81 M R^2-M R^2}{18}\)

I=\(\frac{40 M R^2}{9}\)

Question 35. Three identical rings of mass m and radius r are placed as shown in the figure. Find the moment of inertia of the system about axis XX’.

1. \(\frac{7}{2} m r^2\)
2. \(\frac{5}{2} m r^2\)
3. \(\frac{3}{2} m r^2\)
4. \(\frac{1}{2} m r^2\)

Answer: 1. \(\frac{7}{2} m r^2\)

Moment of Inertia Of System About XX’

I=\(I_1+I_2+I_3\)

Here, \(I_1\)= M.I. of ring about its diameter \({1}{2} m r^2 \)

⇒ \(I_2=\frac{1}{2} m r^2+m r^2=\frac{3}{2} m r^2\)

Similarly, \(I_3=\frac{3}{2} m r^2\)

I =\(\frac{1}{2} m r^2+\frac{3}{2} m r^2+\frac{3}{2} m r^2\)

=\({7}{2} m r^2\)

Question 36. The ratio of the radii of gyration of a circular disc to that of a circular ring, each of the same mass and radius around their respective axes is:

1. \(\sqrt{3}: \sqrt{2}\)
2. \(1: \sqrt{2}\)
3. \(\sqrt{2}: 1\)
4. \(\sqrt{2}: \sqrt{3}\)

Answer: 2. \(1: \sqrt{2}\)

We know that, Radius of gyration is K=\(\sqrt{\frac{I}{M}}\)

Using This Formula We Have, \(M K_1 =M R^2\)

⇒ \(K_1\) =R

And \( M K_2^2 =\frac{M R^2}{2}\)

⇒ \( K_2  =\frac{R}{\sqrt{2}}\)

∴ \(\frac{K_2}{K_1}  =\frac{R}{\sqrt{2} R}=\frac{1}{\sqrt{2}}\)

Question 37. Two bodies have their moments of inertia 1 and 2  respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio:

1. 2: 1
2. 1: 2
3. \(\sqrt{2}: 1\)
4. \(1: \sqrt{2}\)

Answer: 4. \(1: \sqrt{2}\)

K.E. rotation,K=\(\frac{1}{2} I \omega^2\)

Angular momenta, L=100

K=\(\frac{L^2}{2}\)

Here, \(K_1=K_2, I_1=I_1, I_2=2 \mathrm{I}\)

⇒ \(\frac{L_1}{L_2}=\sqrt{\frac{2 I_1 K_1}{2 I_2 K_2}}\)

=\(\sqrt{\frac{I_1}{I_2}}=\sqrt{\frac{I}{2 I}}\)

=\(\frac{1}{\sqrt{2}}\)

Question 38. Three particles, each of mass m gram, are situated at the vertices of an equilateral triangle ABC side/cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram cm² units will be:

1. \(\frac{3}{4} m l^2\)
2. \(2 m l^2\)
3. \(\frac{5}{4} m l^2\)
4. \(\frac{3}{2} m l^2\)

Answer: 3. \(\frac{5}{4} m l^2\)

According to the question

⇒ \(I_{A X} =m l^2+m\left(\frac{l}{2}\right)^2\)

=\(m l^2+\frac{m l^2}{4}\)

=\(\frac{5}{4} m l^2\)

Question 39. A circular disc is to be made by using iron and aluminium so that it acquires a moment of inertia about the geometrical axis. It is possible with:

1. aluminium at the interior and iron surrounding it
2. iron at the interior and aluminium surrounding it
3. using iron and aluminium lives in an alternate order
4. sheet of iron is used at the external surface and aluminium sheet as internal layers

Answer: 1. aluminium in the interior and iron surrounding it

The density of Iron is more than Aluminum.

Question 40. The moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is :

1. \(\frac{2}{3} M R^2\)
2. \(\frac{3}{2} M R^2\)
3. \(\frac{4}{5} M R^2\)
4. \(\frac{5}{4} M R^2\)

Answer: 4. \(\frac{5}{4} M R^2\)

Moment of inertia of a disc about its diameter

Now, according to the perpendicular axis theorem, a moment of inertia of a disc about a tangent passing through rim in the plane of the disc,

I= \(I_d+M R^2\)

I= \(\frac{1}{4} M R^2+M R^2\)

I= \(\frac{5}{4} M R^2\)

Question 41. From a disc of radius R and mass M, a circular hose of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the Centre?

1. \(\frac{13 \mathrm{MR}^2}{32}\)
2. \(\frac{11 \mathrm{MR}^2}{32}\)
3. \(\frac{9 \mathrm{MR}^2}{32}\)
4. \(\frac{15 \mathrm{MR}^2}{32}\)

Answer: 1. \(\frac{13 \mathrm{MR}^2}{32}\)

This Diagram is

Moment of Inertia of disc,

I =\(I_1+I_2+I_3\)

⇒ \(I_1 =\frac{2}{3} m r_2\)

⇒ \(I_2 =I_3=\frac{2}{3} m r^2+m r^2\)

(using parallel axis theorem)

⇒ \(I_3=I_2 =\frac{5}{3} m r^2\)

I =\(\frac{2}{3} m r^2+2 \times \frac{5}{3} m r^2\)

= \(m r^2\left(\frac{2}{3}+\frac{10}{3}\right)=4 m r^2\)

Question 42. Three identical spherical shells, each of mass m and radius r are placed as shown in the figure. Consider an axis XX, which is touching two shells and passing through the diameter of the third shell: The moment of inertia of the system consisting of these three spherical shells about XX’s axis is:

1. \(\frac{11}{5} m r^2\)
2. \(3 m r^2\)
3. \(\frac{16}{5} m r^2\)
4. \(4 m r^2\)

Answer: 4. \(4 m r^2\)

Let I₁, I₂ and I₃ be the Movement of Inertia of three spheres

So, the Moment of Inertia of the spheres about the axis passing through xx’ is,

I=\(I_1+I_2+I_3\)   Equation 1

⇒ \(I_1=\frac{2}{3} m r_2\)

⇒ \(I_2=I_3=\frac{2}{3} m r^2+m r^2\) (using parallel axis theorem)

⇒ \(I_3=I_2 =\frac{5}{3} m r^2\)

⇒ \(I =\frac{2}{3} m r^2+2 \times \frac{5}{3} m r^2\)

=\(m r^2\left(\frac{2}{3}+\frac{10}{3}\right)=4 m r^2\)

Question 43. The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:

1. 2
2. 3
3. 4
4. 1

Answer: 1. 2

According to the parallel axis theorem,\(\mathrm{I}=\mathrm{I}_{\mathrm{cm}}+m d^2\) d is maximum to B

Question 44. The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid¬point and perpendicular to its length is \(l_0\)– Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is:

1. \(l_0+M L^2 / 4\)
2. \(l_0+2 M L^2\)
3. \(l_0+M L^2\)
4. \(l_0+M L^2 / 2\)

Answer: 1. \(l_0+M L^2 / 4\)

Moment of inertia about an axis passing t}rough one end

⇒ \(\mathrm{I}=I_{C M}+m d^2 \)

∴ \(\mathrm{I}=I_0+M\left(\frac{L}{2}\right)^2=I_0+\frac{M L^2}{4}\)

Question 45. Four identical thin rods each of mass M and length l, form a square frame. The moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is:

1. \(\frac{4}{3} \mathrm{Ml}^2\)
2. \(\frac{2}{3} \mathrm{Ml}^2\)
3. \(\frac{13}{3} \mathrm{Ml}^2\)
4. \(\frac{1}{3} \mathrm{Ml}^2\)

Answer: 1. \(\frac{4}{3} \mathrm{Ml}^2\)

From the parallel axis theorem,

Moment of Inertia =\(\frac{M l^2}{2}+M\left(\frac{1}{2}\right)^2=\frac{M l^2}{3}\)

Moment of Inertia of the system =\(\frac{M l^2}{3} \times 4\)

= \(\frac{4}{3} M l^2\)

Question 46. A thin rod of length L and mass M is bent at its midpoint into two halves so that the angle between them is 90°. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is:

1. \(\frac{M L^2}{24}\)
2. \(\frac{M L^2}{12}\)
3. \(\frac{M L^2}{6}\)
4. \(\frac{\sqrt{2} M L^2}{26}\)

Answer: 3. \(\frac{M L^2}{6}\)

Moment of Inertia of the system, I =\(\frac{M(L / 2)^2}{3}+\frac{M(L / 2)^2}{3}\)

=\(\frac{M L^2}{12}+\frac{M L^2}{12}\)

=\(\frac{M L^2}{6}\)

Question 47. The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is:

1. \(M R^2\)
2. \(\frac{1}{2} M R^2\)
3. \(\frac{3}{2} M R^2\)
4. \(\frac{7}{2} M R^2\)

Answer: 3. \(\frac{3}{2} M R^2\)

Moment of Inertia disc about its normal =\(\frac{1}{2} M R^2\)

Moment of Inertia about its one edge =\(M R^2+\frac{M R^2}{2}\)

Moment of Inertia = \(\frac{3}{2} M R^2\)

Question 48. The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is:

1. 2: 3
2. 2: 1
3. \(\sqrt{5}: \sqrt{6}\)
4. \(1: \sqrt{2}\)

Answer: 3. \(\sqrt{5}: \sqrt{6}\)

The radius of gyration of the disc about a tangential axis in the plane of the disc is \(k_1\),

⇒ \(k_1=\frac{5}{4} M R^2=\frac{\sqrt{5}}{2} R\)

(From parallel Axis Theorem) And radius of gyration of a circular ring of the same radius about a tangential axis is given by:

⇒ \(k_2=\frac{3}{2} M R^2=\frac{\sqrt{3}}{\sqrt{2}} R\)

(From parallel Axis Theorem)

⇒ \(\frac{k_1}{k_2} =\frac{\sqrt{5}}{2} R / \frac{\sqrt{3}}{\sqrt{2}} R\)

=\(\frac{\sqrt{5}}{2} \times \frac{\sqrt{2}}{\sqrt{3}}\)

=\(\frac{\sqrt{5}}{\sqrt{6}}\)

Question 49. The angular speed of the wheel of a vehicle is increased from 360 rpm to 1200 rpm in 14 s. Its angular acceleration is :

1. \(2 \pi \mathrm{rad} / \mathrm{s}^2\)
2. \(28 \pi \mathrm{rad} / \mathrm{s}^2\)
3. \(120 \pi \mathrm{rad} / \mathrm{s}^2\)
4. \(1 \mathrm{rad} / \mathrm{s}^2\)

Answer: 1. \(2 \pi \mathrm{rad} / \mathrm{s}^2\)

Initial angular velocity of the wheel,

⇒ \(\omega_i =2 \pi f_o=2 \pi \times \frac{360}{60} \mathrm{rad} / \mathrm{s}\)

=\(12 \pi \mathrm{rad} / \mathrm{s}\)

final angular velocity of wheel, \(\omega_f  =2 \pi f=2 \pi \times \frac{1200}{60} \mathrm{rad} / \mathrm{s}\)

=\(40 \pi \mathrm{rad} / \mathrm{s}\)

⇒ \(\Delta t=14 \mathrm{~s}\)

From the equation of rotational motion

⇒ \(\omega_f  =\omega_i+\alpha \Delta t\)

⇒ \(\alpha  =\frac{\omega_f-\omega_i}{\Delta t}\)

=\( 2 \pi \mathrm{rad} / \mathrm{s}\)

Question 50. A wheel has an angular acceleration of 3.0 rad/sec² and an initial angular speed of 2.00 rad sec. In a time of 2 seconds it has rotated through an angle (in radians) of:

1. 10
2. 12
3. 4
4. 6

Answer: 1. 10

⇒ \(\theta =\omega_0 t+\frac{1}{2} \alpha^2\)

=\((2)(2)+\frac{1}{2}(3)(2)^2\)

=4+6=10

Question 51. A solid cylinder of mass 2 kg and radius 4 cm is rotating about its axis at the rate of 3 rpm. The torque required to stop after the 2π revolution is :

1. \(2 \times 10^{-3} \mathrm{~N}-\mathrm{m}\)
2. \(2 \times 10^{-4} \mathrm{~N}-\mathrm{m}\)
3. \(2 \times 10^{-6} \mathrm{~N}-\mathrm{m}\)
4. \(2 \times 10^{-6} \mathrm{~N}-\mathrm{m}\)

Answer: 4. \(2 \times 10^{-3} \mathrm{~N}-\mathrm{m}\)

Mass, M=2 kg, Radius R=4 cm

Initial angular speed, \(\omega_0=3 \times \frac{2 \pi}{60} \mathrm{rad} / \mathrm{s}\)

=\(\frac{\pi}{10} \mathrm{rad} / \mathrm{s}\)

We know that, \(\omega_2  =\omega_0^2+2 \alpha \theta\)

0 =\(\left(\frac{\pi}{10}\right)^2+2 \cdot \alpha \times 2 \pi \times 2 \pi\)

⇒ \(\alpha  =-\frac{1}{800} \mathrm{rad} / \mathrm{s}^2\)

Now moment of inertia of a solid cylinder,

I=\(\frac{M R^2}{2}=\frac{2 \times\left(\frac{4}{100}\right)^2}{2}=\frac{16}{10^4}\)

Now we know that, Torque,

⇒ \(\tau =\mathrm{I} \times \alpha=\frac{16}{10^4} \times\left(-\frac{1}{800}\right)\)

=\(-2 \times 10^{-6}(\mathrm{Nm})\) .

Question 52. Three objects, A : (a solid sphere), B : (a thin circular disk) and C : (a circular ring), each have the same mass M and radius R. They all spin with the same angular speed co about their symmetry axis. The amount of work (W) required to bring them to rest, would satisfy the relation :

1. \(W_B>W_A>W_C\)
2. \(W_A>W_B>W_C\)
3. \(W_C>W_B>W_A\)
4. \(W_A>W_C>W_B\)

Answer: 3. \(W_C>W_B>W_A\)

Work done required to bring them rest,

⇒ \(\Delta W  =\Delta K E\)

⇒ \(W_A  : W_B: W_C \)

=\(\frac{2}{5} M R^2: \frac{1}{2} M R^2: M R^2 \)

=\(\frac{2}{5}: \frac{1}{2}: 1\)

=4: 5: 10

∴ \(W_C >W_B>W_A\)

Question 53. A rope is around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 30 N?

1. 25 m/s²
2. 0.25 rad/s²
3. 25 rad/s²
4. 5 m/s²

Answer: 3. 25 rad/s²

Torque on the cylinder due to force F  \(\tau=F R\)

and we know that, \(\tau=\mathrm{I} \alpha\)

Where, I= Moment of Inertia of cylinder about axis = \(M R^2\)

and \(\alpha\)= angular acceleration on comparing both the equations,

⇒ \(\alpha=\frac{\tau}{I}=\frac{F R}{M R^2}=\frac{F}{M R}\)

∴ \(\alpha=\frac{30}{3 \times 40 \times 10^{-2}}=25 \mathrm{rad} / \mathrm{s}^2\)

Question 54. A uniform circular disc of radius 50 cm is at rest and is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad s^-2. Its net acceleration in ms^-2 at the end of 2.0 is approximately:

1. 7.0
2. 6.0
3. 3.0
4. 8.0

Answer: 4. 8.0

According to the question,

A uniform circular disc of radius 50 cm is at rest and is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad s^-2.

Angular acceleration, \(\alpha=2 \mathrm{rad} \mathrm{s}^{-2}\)

Angular speed, \(\omega=\alpha t=4 \mathrm{rad} \mathrm{s}^{-1}\)

because centripetal acceleration at the end of 2.0

⇒ \(a_t=\alpha r=2 \times 0.5=1 \mathrm{~m} / \mathrm{s}^2\)

Net acceleration,\(\alpha=\sqrt{a_c^2+a_t^2}\)

=\(\sqrt{(8)^2+(1)^1}\)

=\(\sqrt{65} \approx 8 \mathrm{~m} / \mathrm{s}^2\)

Question 55. Point masses m₁ and m₂ are placed at the opposite ends of a rigid rod of length L and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass, so that the work required to set the rod rotating with angular velocity COQ is minimum, is given by:

1. \(x=\frac{m_1 \mathrm{~L}}{m_1+m_2}\)
2. \(x=\frac{m_1}{m_2} \mathrm{~L}\)
3. \(x=\frac{m_2}{m_1} \mathrm{~L}\)
4. \(x=\frac{m_2 \mathrm{~L}}{m_1+m_2}\)

Answer: 4. \(x=\frac{m_2 \mathrm{~L}}{m_1+m_2}\)

Given

Point masses m₁ and m₂ are placed at the opposite ends of a rigid rod of length L and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass,

Here m₁ and m₂ masses are placed at opposite ends of the rigid rod whose length is L

Moment of Inertia of rod, \(\mathrm{I}=m_1 x^2+m_2(L-x)^2\)

=\(m_1 x^2+m_2 L^2+m_2 x^2-2 m_2 L^2\)

⇒ \(\mathrm{I}_a is\) minima then,

⇒ \(\frac{d \mathrm{I}}{d x}=2 m_1 x+0+2 x m_2-m_2 L\) =0

⇒ \(x\left(2 m_1+2 m_2\right)=2 m_2 L\)

x=\(\frac{m_2 L}{m_1+m_2}\)

Minimum work = Minimum rotational K.E.

Maximum angular moments = Minimum moment of inertia its rotation should be about CM

∴ x=\(\frac{m_2 L}{m_1+m_2}\)

Question 56. An automobile moves on a road with a speed of 50 km hr^-2. The radius of its wheels is 0.45 m and the moment of inertia of the wheel about its axis of rotation is 3 kg m². If the vehicle is brought to rest in 15 s, the magnitude to average torque transmitted by its breaks to the wheel is:

1. 6.66 kg m2 s^-2
2. 8.58 kg m2 s^-2
3. 10.86 kg m2s^-2
4. 2.86 kg m2s^-2

Answer: 1. 6.66 kg m2 s^-2

Given

An automobile moves on a road with a speed of 50 km hr^-2. The radius of its wheels is 0.45 m and the moment of inertia of the wheel about its axis of rotation is 3 kg m². If the vehicle is brought to rest in 15 s

According to question ,Velocity of automobile vehicle is v=\(54 \mathrm{~km} / \mathrm{h}=54 \times \frac{5}{18}\)

And angular velocity, v=\(\omega_0 r\)

⇒ \(\omega_0=\frac{v}{R}=\frac{15}{0.45}=\frac{100}{3} \mathrm{rad} / \mathrm{s}\)