UP Board Class 11 Chemistry Solutions For Chemical Thermodynamics Question And Answers
Question 1. For a process at a particular temperature and pressure G = ΔH- TΔS. It can be written as: – What does the quantity within the bracket indicate?
Answer:
For a process at a particular temperature and pressure G = ΔH- TΔS.
In a process at a given pressure and a temperature of T K, the change in Gibbs free energy (AG) and the change in entropy ofthe universe is expressed by the relation
⇒ \(\begin{aligned}
& \Delta G=-T \Delta S_{\text {univ }} \text { or, }-\Delta G=T \Delta S_{\text {univ }} \\
& \text { Given equation: }-\Delta G=T\left[-\frac{\Delta H}{T}+\Delta S\right]
\end{aligned}\)
Comparing equations [1] and [2] we get that the quantity within the bracket in equation [2] is ΔSuniv.
Question 2. At a particular temperature and pressure, when will the changes in the entropy of the system (ΔSsys) and the surroundings soundings (ΔSsurr) be equal but the opposite in sign in a chemical reaction? In this condition, what will the value of AG be? Will the reaction be spontaneous in this condition?
Answer:
At a particular temperature and pressure, a reaction will be at equilibrium in the reaction ASuniv = 0. Now, ΔSuniv = ΔSsys + ΔSsurr or, ΔSsys + ΔSsurr = 0 or, ΔSsurr =
So, at equilibrium ΔSsys = -ΔSsurr
We know, ΔG = -TΔSuniv
At equilibrium, ΔSuniv = 0, So, ΔG = 0.
Since the reaction is at equilibrium, neither the forward process nor the reverse process is spontaneous.
Question 3. At a given temperature and pressure, for a chemical reaction AH < 0 & AS <0. Is the spontaneity of this reaction dependent upon temperature? If it depends and if the reaction reaches equilibrium at a temperature of Tg, then will the reaction be spontaneous below or above Te?
Answer:
At a given temperature and pressure, a process will be spontaneous in this process ΔG < 0. Again, ΔG = ΔH- TΔS. So, at a given temperature and pressure, ΔH -TΔS < 0 for a spontaneous process. For the given physical change, ΔH < 0 and ΔS < 0. Therefore, for this process. ΔH- TΔS will be less than zero only when |ΔH| is greater than |7ΔS|. Now the value of |TΔS| depends on temperature.
Therefore, the spontaneity of this process will depend on temperature. Ifthe equilibrium temperature ofthe process is Tg, then at equilibrium ΔG = 0 = ΔH- TgΔS or, ΔH = Tg x AS A process occurs spontaneously ΔG < 0 . or, ΔH- TΔS < 0 [ v ΔG = ΔH- TΔS ] Therefore, ΔH- TΔS < 0 or, TgΔS- TΔS <0 or, (Te- T)ΔS < 0 For the given process, AS < 0. So, Tg-T> 0 or, Tg> T Therefore, the given process will be spontaneous at a temperature below the equilibrium temperature.
Question 4. A physical change at a fixed pressure attains equilibrium at 353 K. In this process, ΔH > 0 and AS > 0. What will be the direction (from left to right or right to left) of this process at 350 K and 355 K?
Answer:
For a spontaneous process at constant temperature and pressure, AG = AH- TAS and AG < 0. At equilibrium, ΔG = 0 or, ΔH- TΔS = 0 or, ΔH = TΔS [T’ = equilibrium temperature = 353 K]
ΔH = 353 x ΔS and ΔG = ΔH- TΔS = (353- DΔS For this physical change, ΔS > 0. Hence, AG will be negative if 353- T < 0 or, T > 353K. This indicates that the process will be spontaneous above 353K and it will be non-spontaneous when T < 353K (as at this condition ΔG > 0 ). Therefore, at 355K the direction ofthe process will be left to right and at 350 K the direction ofthe process will be from right to left.
Question 5. At a given temperature and pressure, for a chemical reaction AH > 0 and AS < 0. The reaction is non-spontaneous at all temperatures. But the reverse reaction is spontaneous at all temperatures—Give reason.
Answer:
At constant temperature and pressure, a process will be spontaneous if ΔG < 0 for the process Again, ΔG = ΔH- TΔS
For the given reaction, ΔH > 0 and ΔS < 0.
Hence, from equation [1] we get, AG is positive for this process. So it is non-spontaneous. But for the same temperature and pressure, the AG value of the reverse reaction must be negative. Therefore, the reverse reaction is spontaneous.
Question 6. The results obtained by applying the mathematical form of the first law of thermodynamics for different processes are given below. Identify the processes (m = P-V work only):ΔU = 0, q + w = 0, q = 0, ΔU < 0. w < 0 q= O,ΔV>O , ΔU =w=0
Answer:
Given
The results obtained by applying the mathematical form of the first law of thermodynamics for different processes are given below.
According to the first law of thermodynamics, ΔU=q +w…..[1]
In the process, ΔU = 0. U is a state function. So, in a cyclic process, Its change is zero. So, from equation (1], q + w = 0. Thus, the given conditions indicate a cyclic process.
Again in the isothermal process, the change in internal energy for an ideal gas is zero. Thus according to equation [1], for isothermal change of an ideal gas, q + w = 0. Thus, the given conditions indicate an isothermal change.
In the process, q = 0. So, Δ = w or -ΔU = -w (from equation [1]).
As q = 0 , the process is adiabatic. In such a process, the work done by the system (Δv < 0) is equal to a decrease in internal energy (Δt< 0). So, the given conditions indicate that the process is adiabatic and work is done by the system.
As q = 0 and if (P-V work) = 0, from equation [1], At)1 also becomes zero, q = 0 indicates that the process is adiabatic. Since w =’ 0 and ΔV> 0, the volume of the system increases in process but no work is done by the system. This happens in case of an expansion against zero pressure. Thus, the given conditions indicate the adiabatic expansion against zero pressure
Question 7. The entropy of the system decreases on condensation of a vapour though it occurs spontaneously. Explain.
Answer:
The entropy of the system decreases on condensation of a vapour though it occurs spontaneously.
On condensation of vapour, the entropy change of the system is, ΔS = Sliquid-Svapour. ΔS= Sliquid– Svapour, the entropy of the system decreases in the process. Condensation of a vapor is an exothermic process. Hence, the entropy of the surroundings increases. However, the increase in entropy of the surroundings is greater than the decrease in entropy of the system. So, Δ Stoatal is always positive in this process.
ΔStotal = ΔSsytem +ΔSsurroundings
So, condensation of a vapor is a spontaneous process.
Question 8. The formation of ice from water is exothermic, but water does not convert into ice spontaneously at ordinary temperature and pressure. Why?
Answer:
The formation of ice from water is exothermic, but water does not convert into ice spontaneously at ordinary temperature and pressure.
At a given temperature and pressure, a process will be spontaneous if it occurs with a decrease in free energy.
Again, at a fixed temperature and pressure, the free energy change of a system in a process is, ΔG = ΔH- TΔS; where ΔH and ΔS are enthalpy and entropy change of the system respectively.
During the conversion of water Into Ice, the entropy of the system decreases because the entropy of a liquid Is greater than that of a solid. So, for the conversion of water Into Ice, AS Is -ve.
Again, All Is also- ve as It Is an exothermic process. Thus, both ΔH and TΔS are -ve. But at ordinary temperature and pressure, |TΔS| Is greater than|TΔS]. Hence, the value of ΔG becomes |ΔH|. So, the conversion of water Into Ice at ordinary temperature and pressure Is not spontaneous.
Question 9. For the reaction \(\mathrm{CH}_4(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CH}_3 \mathrm{OH}(\mathrm{g}) ;\) AH0 = negative at 25°C. If the standard enthalpies of combustion of CH4(g) and CH3OH(g) at 25°C are -x kj mol-1 & -y kl.mol-1 respectively, then will the value of x be less than, greater than, or equal to the value of y?
Answer:
Given
For the reaction \(\mathrm{CH}_4(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CH}_3 \mathrm{OH}(\mathrm{g}) ;\) AH0 = negative at 25°C. If the standard enthalpies of combustion of CH4(g) and CH3OH(g) at 25°C are -x kj mol-1 & -y kl.mol-1 respectively,
⇒ \(\begin{array}{r}
\mathrm{CH}_4(\mathrm{~g})+2 \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(l) ; \Delta H^0=-x \mathrm{~kJ} \\
\mathrm{CH}_3 \mathrm{OH}(\mathrm{g})+\frac{3}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+2 \mathrm{H}_2 \mathrm{O}(l) ; \\
\Delta H^0=-y \mathrm{~kJ}
\end{array}\)
Subtracting equation [2] from equation [l], we obtain
\(\mathrm{CH}_4(g)+\frac{1}{2} \mathrm{O}_2(g) \rightarrow \mathrm{CH}_3 \mathrm{OH}(g) ; \Delta H^0=(y-x) \mathrm{kJ}\)
According to the question, (y-x) = negative. Thus, x > y.
Question 10. At a certain temperature and pressure, ΔH = 0 for the reaction: X + X = X2. Show that the reaction is non-spontaneous at this temperature and pressure.
Answer:
At a certain temperature and pressure, for a chemical reaction, ΔG = AH- TAS.
Now, AH = 0 for given the reaction. So, AG = -TAS In the given reaction, X2 is produced from two atoms of X. So, the entropy of the system decreases. So, AS < 0.
AG =-T x (negative quantity) = positive quantity The positive value of AG indicates that the reaction is non-spontaneous.
Question 11. The magnitude of work done by a gas in a reversible expansion is greater than that in an irreversible expansion provided the initial and final states are identical in both processes —explain
Answer:
The magnitude of work done by a gas in a reversible expansion is greater than that in an irreversible expansion provided the initial and final states are identical in both processes
Suppose, an ideal gas expands isothermally from its initial state P1 V1 to its final state P2 V2.
A reversible process consists of an infinite number of small steps, and at each step, the driving force, is infinitesimally greater than die opposing force. Suppose, in a reversible expansion of an ideal gas, die external pressure of the gas at a step of the process is decreased by a very small amount of dP, causing the increase in volume of the gas by dV. The work done by the gas will be, dw = ~{Pex~dP)dV = -PdV [v Pv- dP = P (pressure of the gas) and dP x dV is very small as in the P-V diagram the points, m, and n are very close and pressure in these two points are not much different]. In the above diagram, PdV is given by the area of the strip, mnqp. The total work done in the reversible process will be equal to the sum of the die areas of all such strips. Thus, in such a process, work is done.
Absolute value of work done,|w| = area ABNM Now, in isothermal irreversible expansion, suppose, the gas is expanded from volume to V2 against an external pressure which is equal to the final pressure of the gas. In this process work done,
⇒ \(w=\int_{V_1}^{V_2} P_2 d V=-P_2 \int_{V_1}^{V_2} d V\left[P_2=\text { constant during expansion }\right]\)
The absolute value of work done,|w|=P2(V2– V1) =area ABM:
From the graphs, it is clear that work done in reversible isothermal expansion is greater than that in irreversible isothermal expansion since the area of ABNM is greater than that of ABNE. This also indicates that the work involved in a process depends upon the path (or nature) of the process.
Question 12. A gas cools down during adiabatic expansion and it becomes hot during adiabatic compression —explain
Answer:
A gas cools down during adiabatic expansion and it becomes hot during adiabatic compression
In an adiabatic process, heat is not exchanged between the system and its surroundings. In this process, if the gas is expanded, then the gas does work at the expense of its internal energy. As a result, the internal energy as well as the temperature of the gas decreases due to the adiabatic expansion of an ideal gas.
As no heat is exchanged between the system and its surroundings in an adiabatic process, any work done on the gas during adiabatic compression increases the internal energy of the gas. As a result, the temperature of the gas increases.
Question 13. Given: A(s) + B2(g)→AB2(g);ΔHº = -x kJ \(\mathrm{A}(\mathrm{s})+\frac{3}{2} \mathrm{~B}_2(\mathrm{~g}) \rightarrow \mathrm{AB}_3(\mathrm{~g}) ; \Delta H^0=-y \mathrm{~kJ}\)
Answer: Multiplying the equation by 2, we get,
2A(s) + 2B2(g) 2AB2(g); ΔH0 = -2xkJ………[3]
Writing the equation in a reverse manner and multiplying both sides by 2, we get,2AB3(g) 2A(s) + 3B2(g); AH0 = +2y kJ Adding equations [3] and [4], we get,
A(5) + 2B2(g) + 2AB3(g-2A(s) + 2AB2(g) + 3B2(g); AH0 = (2y-2jc)kJ
2AB3(g)→2AB2(g) + B2(g); AH0 = +2ykJ
Therefore, the standard reaction enthalpy for the given reaction = 2(y- x) kJ.
Question 14. At 25°C the standard enthalpy of formation of freon gas (CHC1F2) is -480.0 kj.mol-1. Write down the thermochemical equation representing the formation reaction of the compound.
Answer:
Given
At 25°C the standard enthalpy of formation of freon gas (CHC1F2) is -480.0 kj.mol-1.
The constituent elements of the compound, are CHC1F2 carbon, hydrogen, chlorine, and fluorine. The standard states of these elements are C(graphites), H2(g), Cl2(g), and F2(g). Thus, the thermochemical equation for the formation reaction-
⇒ \(\mathrm{C}(\text { graphite, } s)+\frac{1}{2} \mathrm{H}_2(g)+\frac{1}{2} \mathrm{Cl}_2(g)+\mathrm{F}_2(g) \rightarrow \mathrm{CHClF}_2(g) ;\)
⇒ \(\Delta H_f^0\left[\mathrm{CHClF}_2(g)\right]=-480.0 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)
Question 15. For each of the given changes, state whether the final enthalpy Is greater or less than the initial enthalpy: H2Q(r)→ H2O(l), H2O(g) H2O(l)
Answer:
Change is a melting process. So, it is an endothermic process. Hence, in this process, ΔH = +ve.
ΔH=H[H20(l)]- H[H20(s)]. As ΔH > 0, H[H2O(l)] > H[H2O(S)], indicating greater enthalpy for the final state than the initial state.
Change is a condensation process and so, it is an exothermic process. Hence in this process AH = -ve. AH = H[H20(/)]-H[H20(g)] Since AH < 0, H[H20(/)] < H[H20(g)]. Thus enthalpy of the final state is less than that of the initial state.
Question 16. There occurs no exchange of heat between a system and its surroundings in an adiabatic process. So, the change in entropy of the system is zero in this process. Justify the statement.
Answer:
There occurs no exchange of heat between a system and its surroundings in an adiabatic process. So, the change in entropy of the system is zero in this process.
The statement is incorrect. It is applicable only for a reversible adiabatic change.
We know, the change in entropy of a system in a reversible process \(d S=\frac{\delta q_{r e V}}{T}\) (where 6qrev is heat lost or gained by the system in the process at 7’K). Now, for the reversible adiabatic process, our = 0.
Therefore, dS – 0. So, the entropy change Is zero in a reversible adiabatic process. In the case of an irreversible process, there is no relation between the entropy change and the heat lost or gained by the system in the process.
However, it can be shown that the entropy change in an irreversible process is \(d S>\frac{\delta q_{l r}}{T}\) (where oq[rr is the heat lost or gained by the system in the process at T K). Now, in an irreversible adiabatic process 6q(rr = 0. So, dS (or AS) > 0. Tilus the entropy of the system increases in an irreversible adiabatic process.
Question 17. Mg) + A(g)→A2(g); these types of reactions are generally exothermic. Explain.
Answer:
Mg) + A(g)→A2(g); these types of reactions are generally exothermic.
In the reaction, one molecule A2(g) is formed from two atoms of A(g). Thus, the entropy of the system decreases. For any chemical reaction at fixed temperature and pressure, ΔG =ΔH- TΔS. For the given reaction, ΔS<0. The reaction will be spontaneous if ΔG < 0.
So, negative quantity = ΔH- (T X negative quantity) = ΔH + positive quantity
∴ ΔH = (-ve) quantity- (+ye) quantity ; So, ΔH < 0
∴ The given reaction is exothermic.
Question 18. At ordinary temperature and pressure, solid NH4C1 dissolves in water to form NH4(aq) and Cl(aq) ions. The process is endothermic. Indicate the signs (+ or-) of ΔSsys, ΔSsurr, ΔH And ΔG
Answer:
As the process is endothermic, AH > 0.
At ordinary temperature and pressure, the dissolution of solid NH4C1 occurs spontaneously, so AG < 0.
NH+4 and Cl- ions in the crystal lattice of NH4C1 are held at fixed positions and consequently, they are not able to move. But in an aqueous solution of NH4C1, NH, and Cl- ions are distributed throughout the solution. Naturally, the randomness of the ions in aqueous solution of NH4C1 is greater than that in solid NH4C1. Hence, in the dissolution process of NH4CI, ΔSsys > 0.
As the process is endothermic, the system absorbs heat from the surroundings. Consequently, the surroundings lose heat. As a result, the entropy of the surroundings decreases (ASsurr < 0).
However, the increase in the entropy system is greater than the decrease in the entropy of the surroundings. So, the net entropy change of the system and its surroundings is always positive, and the process occurs spontaneously.
Question 19. Classify as an open, closed, or isolated system:
- A cup of coffee placed on a table
- Water in a beaker is boiled by heating
- Lead nitrate is heated in a test tube
- Solid NH4Cl is heated in a closed vessel
- Substances present in a soda-water bottle
- Mercury enclosed in the thermometer
Answer:
- Open system
- Open system
- Open system
- Closed system
- Closed system
- Closed system
Question 20. Assuming experimental conditions are the same, compare (ΔH-ΔU) values for the given reactions
- \(\mathrm{H}_2(g)+\frac{1}{2} \mathrm{O}_2(g) \rightarrow \mathrm{H}_2 \mathrm{O}(l)\)
- \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)
Answer: In case of reaction (1) \(\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{g})\)
Therefore , \(\Delta H-\Delta U=\Delta n R T=-\frac{3}{2} R T\)
In case of reaction \(\Delta n=1-\left(1+\frac{1}{2}\right)=-\frac{1}{2}\)
Therefore, \(\Delta H-\Delta U=\Delta n R T=-\frac{1}{2} R T\)
Hence, the magnitude of H-U is greater in the case of 2
In case of reaction \(\Delta n=1-\left(1+\frac{1}{2}\right)=-\frac{1}{2}\)
Hence, the magnitude of (AH- AU) is greater in the case of 2
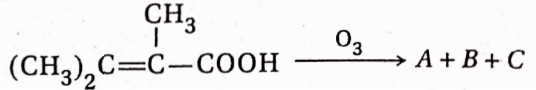, A, B, C in the above reaction are respectively—
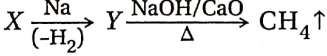In this reaction, X and Y are-