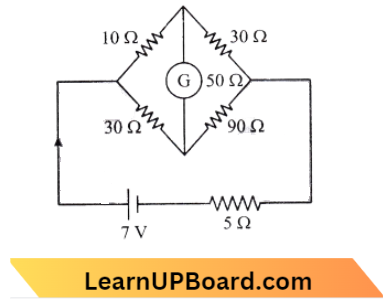
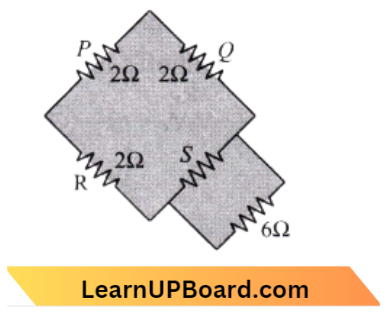
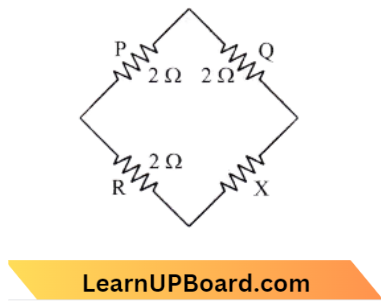
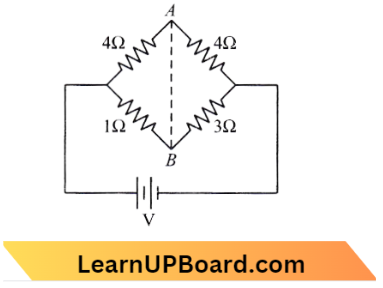
NEET Physics

Moving Charges And Magnetism

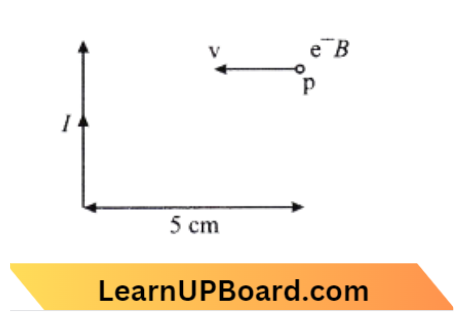
Question 1. An infinitely long straight conductor carries a current of 5 A as shown. An electron is moving with a speed of 10⁵ m/s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant: (Electron, v = 10⁵ m/s)

1. 4 x 10^-20N
2. 8π X 10^-20N
3. 4π x 10^-20N
4. 8 x 10^-20N

Answer: 4. 8π x 10^-20N

Given, I =5 \(\mathrm{~A}\)

⇒ \(V_e =10^5 \mathrm{~m} / \mathrm{s}\)

r =\(20 \mathrm{~cm}=0.2 \mathrm{~m}\)

We know that due to the magnetic field generated by the wire, the electron will experience a force,

F= \(q v \times B\)

Since the angle is \(90^{\circ}\) hence,

F =\(q v_e B\)  →  Equation 1

⇒ \(\mathrm{~B}=\frac{\mu_0 I}{2 \pi r} =2 \frac{\mu_0}{4 \pi} \frac{I}{r}\)

=2 \(\times 10^{-7} \times \frac{5}{0.2}\)

B =\(\frac{2 \times 50}{2} \times 10^{-7}\)

=5 \(\times 10^{-6}\) →  Equation 2

From eqn (1),

F =1.6 \(\times 10^{-19} \times 10^5 \times 5 \times 10^{-6}\)

=8 \(\times 10^{-20} \mathrm{~N}\)

Question 2. A metallic rod of mass per unit length 0.5 kg m^-1 is lying horizontally on a smooth inclined plane which makes an angle of 30° with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of induction 0.25 T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is:

1. 14.76 A
2. 5.98 A
3. 7.14A
4. 11.32 A

Answer: 4. 11.32 A

According to the question, For equilibrium,

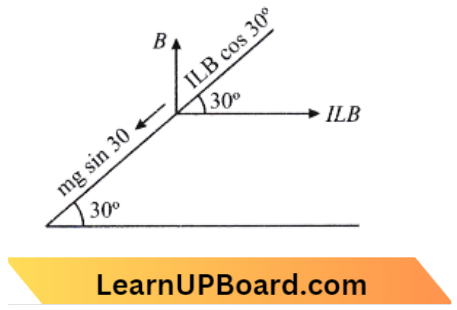
m g \(\sin 30^{\circ} =I l B \cos 30^{\circ}\)

I =\(\frac{m g}{l B} \tan 30^{\circ} \)

= \(\frac{0.5 \times 9.8}{0.25 \times \sqrt{3}}\)

⇒ \(\left.=1  \sin \theta=30^{\circ} B=0.25 \mathrm{~T}\right\}\)

= 11.32 \(\mathrm{~A}\)

Read and Learn More NEET Physics MCQs

Question 3. When a proton is released from rest in a room, it starts with an initial acceleration a₀ towards the west. When it is projected towards the north with a speed v₀ it moves with an initial acceleration 3a₀ towards the west. The electric and magnetic fields in the room are:

1. \(\frac{m a_0}{e}\) west, \(\frac{2 m a_0}{e v_0}\) up
2. \(\frac{m a_0}{e}\) west, \(\frac{2 m a_0}{e v_0}\) down
3. \(\frac{m a_0}{e}\) east, \(\frac{3 m a_0}{e v_0}\) up
4. \(\frac{m a_0}{e}\) east, \(\frac{3 m a_0}{e v_0}\) down

Answer: 2. \(\frac{m a_0}{e}\) west, \(\frac{2 m a_0}{e v_0}\) down

Acceleration of charge particle,\(\vec{a}=\frac{q}{m}(\vec{E}+\vec{V} \times \vec{B})\)

Released from rest

a= \(\frac{q E}{m} \text { (west) } \)

E= \(\frac{m a_0}{e} \text { (west) }\)

When it is projected towards the north, acceleration due to magnetic force =2 \(a_0\)

Magnetic field =\(\frac{2 \cdot m a_0}{e v_0}( down )\)

Question 4. A long straight wire carries a certain current and produces a magnetic field \(2 \times 10^{-4} \frac{\text { Weber }}{\mathrm{m}^2}\) at a perpendicular distance of 5 cm from the wire. An electron situated at 5 cm from the wire moves with a velocity of 107 m/s towards the wire perpendicular to it. The force experienced by the electron will be (change on electron 1.6 x 10^-19C):

1. 3.2 N
2. 3.2 x10^-16N
3. 1.6 x 10^-16N
4. Zero

Answer: 2. 3.2 x10^-16N

From the question, Velocity of electron \(\mathrm{v}=10^7 \mathrm{~m} / \mathrm{s}\)

Magnetic field, B=2 \(\times 10^{-4} \mathrm{~Wb} / \mathrm{m}^2\)

Then magnitude of force experienced by the electron, i.e.

F=\(e v B \sin \theta\)

V and B are perpendicular to each other

= \(e v B \sin 90^{\circ}\)

=1.6 \(\times 10^{-19} \times 10^7 \times 2 \times 10^{-4} \times 1 \)

=3.2 \(\times 10^{-16} \mathrm{~N}\)

Question 5. A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected in the region such that its velocity is pointed along the direction of fields, then the electron:

1. speed with decreased
2. speed with increase
3. will turn towards the left of the direction of motion
4. with a turn towards the right direction motion

Answer: 1. speed with decreased

According to the question, it is clear that field B does not apply force. Field E will apply a force opposite to the velocity of the electron this speed will decrease.

Question 6. The magnetic force acting on a charged particle of charge \(-2 \mu \mathrm{C}\) in a magnetic field of 2T acting in y direction, when the particle velocity is (\((2 \hat{i}+2 \hat{j}) \times 10^6 \mathrm{~ms}^{-1}\) is:

1. 8 N in z-direction
2. 4 N in z-direction
3. 8 N in y-direction
4. 4 N in z-direction

Answer: 1. 8 N in z-direction

Magnetic Lorentz force, \(\vec{F}=q(\vec{V} \times \vec{B})\)

⇒ \(\vec{F}=-2 \times 10^{-6}(2 \hat{i}+3 \hat{j})+2 \hat{j} \times 10^6\)

⇒ \(\vec{F}=-2 \times 10^{-6}(2 \hat{i}+2 \hat{j}) \times 10^6\)

∴ \(\vec{F}=-8 \hat{k} \mathrm{~N}\)

Question 7. When a charged particle moving with velocity \(\vec{v}\) is subjected to a magnetic field of induction \(\vec{B}\), the force on it is non-zero. This implies that:

1. the angle between is either zero or 180°.
2. the angle between is necessarily 90°.
3. the angle between can have any value other than 90°.
4. angle between can have any value other than zero and 180°.

Answer: 4. the angle between can have any value other than zero and 180°.

⇒ \(\vec{F} =q(\vec{V} \times \vec{B})\)

=\(q v B \sin \theta\)

Therefore, when \(\theta=0^{\circ}\) or \(\theta=180^{\circ}\)

F=0

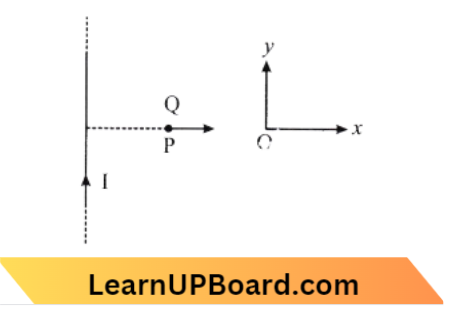
Question 8. A very long straight wire carries a current I. At the instant when a charge + Q at point P has velocity v, as shown, the force on the charge is:

1. along y
2. opposite y
3. along x
4. opposite x

Answer: 1. along y

According to Fleming’s left-hand rule direction of force is along the axis when is perpendicular to the wire,

⇒ \(\vec{F}=Q(\vec{v} \times \vec{B})\)

B due to I is acting inwards is into the paper, \(\mathrm{v}\) is along or:

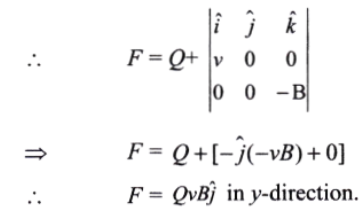
Question 9. A charge ‘q’ moves in a region where the electric field and the magnetic field both exist, then the force on it is:

1. \(q(\vec{v} \times \vec{B})\)
2. q \(\vec{E}+q(\vec{v} \times \vec{B})\)
3. q \(\vec{E}+q(\vec{B} \times \vec{v})\)
4. q \(\vec{E}+q(\vec{B} \times \vec{v})\)

Answer: 2. q \(\vec{E}+q(\vec{v} \times \vec{B})\)

Lorentz force, \(\vec{F}_v =\vec{F}_e+\vec{F}_m \)

= q \(\vec{E}+q(\vec{V} \times \vec{B})\)

Question 10. Tesla is the unit of:

1. magnetic flux
2. magnetic field
3. magnetic induction
4. magnetic moment

Answer: 3. magnetic field

SI unit of magnetic induction is tesla (T). If a charged particle of one coulomb moving at a right angle to a magnetic field with a velocity of lms^-1 experiences a force of 1 N at that point, the magnetic field induction is said to be one tesla.

∴ \( 1 \mathrm{~T}=1 \mathrm{NA}^{-1} \mathrm{~m}^{-1}\)

Question 11. Ionized hydrogen atoms and a-particles with the same momenta enter perpendicular to a constant magnetic field, B. The ratio of the radii of their paths r_H: r_a will be:

1. 1:2
2. 4: 1
3. 1: 4
4. 2: 1

Answer: 4. 2: 1

From equation: \(q_{\mathrm{H}}=e \text { and } q_\alpha\)=2 e

For circular motion, \(\frac{m v^2}{r}\) =B q v

r =\(\frac{m v}{B q}\)

⇒ \(m_1 v_1\) and B are constant

r \(\propto \frac{1}{q} \)

∴ \(\frac{r_{\mathrm{H}}}{r_\alpha}=\frac{q_\alpha}{q_{\mathrm{H}}}=\frac{2 e}{e}=\frac{2}{1}\)=2: 1

Question 12. An electron is moving in a circular path under the influence of a transverse magnetic field of 3.57 x 10^-2 T. If the value of E/M is 1.76 x 10¹¹ C/kg, the frequency of revolution of the electron is:

1. 1 GHz
2. 100 MHz
3. 62.8 MHz
4. 6.28

Answer: 1. 1 GHz

The radius of a charged particle in a magnetic field is, \(r=\frac{m v}{q \mathrm{~B}}\)

And time taken to complete the circle, \(T=\frac{2 \pi r}{V}\)

⇒ \(\frac{T}{2 \pi}=\frac{m}{q B}\)

⇒  \(\omega=\frac{2 \pi}{T}=\frac{q B}{m}\)

Here, q=e, \(\frac{e}{m}=1.76 \times 10^{11} \mathrm{C} / \mathrm{kg}\)

and \(\frac{2 \pi}{T}=\frac{e B}{m}\)

⇒  \(\boldsymbol{f}=\frac{1}{2 \pi} \frac{e}{m} \mathrm{~B}\)

= \(\frac{1}{2 \pi} \times 1.76 \times 10^{11} \times 3.57 \times 10^{-2}\)

= \(1.0 \times 10^9 \mathrm{~Hz}\)

= 1GHz

Question 13. An electron moving in a circular orbit of radius r makes n rotations per second. The magnetic field produced at the center has magnitude:

1. \(\frac{\mu_0 n e}{2 \pi r}\)
2. zero
3. \(\frac{\mu_0 n^2 e}{t}\)
4. \(\frac{\mu_0 n e}{2 r}\)

Answer: 4. \(\frac{\mu_0 n e}{2 r}\)

We know that,

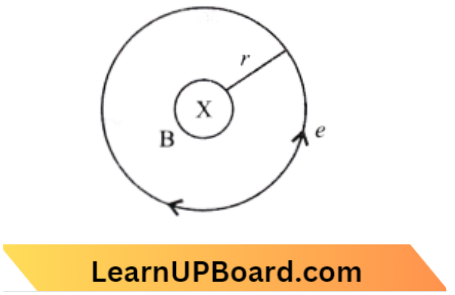
I=\(\frac{q}{t}\)

If an electron is moving in a circular orbit of radius r then,

q=e a\( \omega t\)=T

I =\(\frac{e}{T}=\frac{e}{\frac{2 \pi}{\omega}}\)

= \(\frac{\omega e}{2 \pi}=\frac{2 \pi n e}{2 \pi}\)=n e

∴ magnetic field produced at the centre is B=\(\frac{\mu_0 I}{2 R}=\frac{\mu_0 n e}{2 r}\)

Question 14. A proton and an alpha particle both enter a region of uniform magnetic field B, moving at right angles to the field B. If the radius of circular orbits for both the particles is equal and the kinetic energy acquired by the proton is 1 MeV, the energy acquired by the alpha particle will be:

1. 4 MeV
2. 0.5 MeV
3. 1.5 MeV
4. 1 MeV

Answer: 4.

We know that radius in magnetic fields of a circular orbit is R \(\mathrm{R}=\frac{m V}{q B}=\sqrt{\frac{2 m E}{q B}}\)

In a circular orbit, the total energy of a moving particle.

E= \(\frac{q^2 B^2 R^2}{2 m}\)

When a proton enters the region of the magnetic field then,

⇒  \(E_P =\frac{e^2 B^2 R^2}{2 m_{\mathrm{p}}}\)  →  Equation 1

⇒  \(M_P\)  = mass of proton

Again when \alpha-particle enters the region of the magnetic field then,

⇒  \(E_\alpha=\frac{(2 e)^2 B^2 R^2}{2\left(4 m_{\mathrm{p}}\right)}\) →  Equation 2

since \(m_\alpha=\Delta m_p \text { given }\}\)

Now from eq. (1) and (2)

⇒  \(\frac{E_\alpha}{E_p}=\frac{(2 e)^2 \times B^2 \times R^2}{2 \times 4 m_{\mathrm{p}}} \times \frac{2 \times m_{\mathrm{p}}}{e^2 \times B^2 \times P^2} \)

⇒  \(\frac{E_\alpha}{\dot{E}_p}\)=1

∴ \(E_\alpha=E_P=1 \mathrm{MeV} \)

Question 15. Under the influence of a uniform magnetic field, a charged particle moves with constant speed v in a circle of radius R. The period of rotation of the particle:

1. depends on v and not on R
2. depends on R and not on v
3. is independent of both v and R
4. depends on both v and R

Answer: 3. is independent of both v and R

The time period of the circular motion of the charged particles is

T=\(\frac{2 \pi r}{v}=\frac{2 \pi}{v} \times \frac{m v}{B q}\)

T=\(\frac{2 \pi m}{B q}\)

which is independent of both v and R

Question 16. A particle mass m, charge Q, and kinetic energy T enter a transverse uniform magnetic field of induction \(\vec{B}\)After 3 s the kinetic energy of the particle will be:

1. 3 T
2. 2T
3. T
4. AT

Answer: 3. T

After passing through a magnetic field, the magnitude of its mass and velocity of the particle remain the same, So its energy does not change i.e. K.E. will remain T.

Question 17. A charged particle moves through a magnetic field in a direction perpendicular to it. Then the:

1. speed of the particle remains unchanged
2. the direction of the particle remains unchanged
3. acceleration remains unchanged
4. velocity remains unchanged

Answer: 1. The speed of the particle remains unchanged

A charged particle moves through a magnetic field in a direction perpendicular to it. Then the speed of the particle remains unchanged

Question 18. A charged particle of charge q and mass m enters perpendicularly in a magnetic field B. The Kinetic energy of the particle is E, and the frequency of rotation is:

1. \(\frac{q B}{m \pi}\)
2. \(\frac{q B}{2 \pi m}\)
3. \(\frac{q B E}{2 \pi m}\)
4. \(\frac{q B}{2 \pi E}\)

Answer: 2. \(\frac{q B}{2 \pi m}\)

We have, Magnetic force = centripetal force

qvB =\(\frac{m v^2}{r}\)

qvB =\(m r \omega^2 \)

⇒  \(\omega^2 =\frac{q v B}{m r}=\frac{q(r \omega) B}{m r}\)

Angular frequency, \(\omega=\frac{q B}{m}\)

If v is the frequency of rotation, then \omega=2 \pi v

v=\(\frac{\omega}{2 \pi}\)

⇒  \(\mathrm{v}=\frac{q B}{2 \pi m}\)

Since the resultant expression\(\frac{q}{m}\) is known as a specific charge. It is sometimes denoted by \(\alpha\)

So, \(\omega=B \alpha \text { and } v=v=\frac{B \alpha}{2 \pi}\)

Question 19. Current is flowing in a coil of area A and number of turns N, then magnetic moment of the coil, M is equal to:

1. NiA
2. \(\frac{N i}{A}\)
3. \(\frac{N i}{\sqrt{A}}\)
4. \(N^2 A i\)

Answer: 1. NiA

If a coil contains N turns, I is the current running through it, and A is the coil’s area, then the magnetic dipole moment, or simply the magnetic moment of the coil, M = NiA

When a charged particle enters a magnetic field region at a velocity perpendicular to B, it takes a circular path

Question 20. A 10 eV electron is circulating in a plane at a right angle to a uniform field of magnetic induction 10^-4 Wb/m² (= 1.0 gauss). The orbital radius of the electron is:

1. 12 cm
2. 16 cm
3. 11cm
4. 18 cm

Answer: 3. 11cm

A maximum force acting perpendicular to the direction of B, as well as v, is experienced by a charged particle moving perpendicular to the direction of B. As a result of this force, the charged particle will travel a circular path in the magnetic field of radius r, which is given by,

⇒ \(\frac{m v^2}{r}=q v B\)

Now, \(\mathrm{KE} of electron =10 \mathrm{eV}\)

⇒ \(\frac{1}{2} m v^2 =10 \mathrm{eV} \)

⇒ \(\frac{1}{2} \times\left(9.1 \times 10^{-31}\right) v^2 =10 \times 1.6 \times 1.6 \times 10^{-19}\)

⇒ \(v^2 =\frac{2 \times 10 \times 1.6 \times 10^{-19}}{9.1 \times 10^{-31}}\)

⇒ \(v^2 =3.52 \times 10^{12}\)

v =1.88 \(\times 10^6 \mathrm{~m}\)

or Now the radius of the circular path,

r=\(\frac{m v}{q b}=\frac{9.1 \times 10^{-31} \times 1.88 \times 10^6}{1.6 \times 10^{-19} \times 1^{-4}}=11 \mathrm{~cm}\)

Question 21. A uniform magnetic field acts right angles to the direction of motion of an electron. As a result, the electron moves in a circular path of radius 2 cm. If the speed of electrons is doubled, then the radius of the circular path will be:

1. 2.0 cm
2. 0.5 cm
3. 4.0 cm
4. 1.0 cm

Answer: 3. 4.0 cm

The centripetal force (= \(\mathrm{mv}^2 / \mathrm{r})\) required for motion along a circular path of radius r is generated by the external magnetic field’s force F on the charged particle.

⇒ \(q v B =\frac{m v^2}{r} \text { or } r=\frac{m v}{q B} \)

r \(\propto \mathrm{V}[\frac{m}{q B}=\text { constant }]\)

∴ When v is doubled, the radius is also doubled, Hence, radius r = 2 x 2 = 4 cm.

Question 22. An alternating electric field of frequency v is applied across the dees (radius = R) of a cyclotron that is being used to accelerate protons (mass = m). The operating magnetic field used in the cyclotron and the kinetic energy (K) of the proton beam, produced by it, are given by:

1. B=\(\frac{m v}{e} and K=2 m \pi^2 R^2\)
2. B=\(\frac{2 \pi m v}{e} and K=m^2 \pi v R^2\)
3. B=\(\frac{2 \pi m v}{e} and K=2 m \pi^2 v^2 R^2\)
4. B=\(\frac{m v}{e} and K=m^2 \pi v R^2\)

Answer: 3. B=\(\frac{2 \pi m v}{e} and K=2 m \pi^2 v^2 R^2\)

We Know That

Frequency,v =\(\frac{e \mathrm{~B}}{2 \pi m}\),

⇒ \(\mathrm{KE} =\frac{1}{2} m v^2 a w\)

R =\(\frac{m v}{e B}\)

Radius,R=\(\frac{m v}{e B}\)

Velocity, v=\(\frac{\pi R}{T / 2}=\frac{2 \pi R}{T}=2 \pi R v\)

Radius, R=\(\frac{m(2 \pi R v)}{e B}\)

Magnetic field, B =\(\frac{2 \pi m v}{e} \)

⇒ \(\mathrm{KE} =\frac{1}{2} m v^2=\frac{1}{2} m(2 \pi \mathrm{R} v)^2\)

= \(2 m \pi^2 v^2 R^2\)

Question 23. A beam of cathode rays is subjected to crossed Electric field (E) and Magnetic field (B). The fields are adjusted such that the beam is not deflected. The specific charge of the cathode rays is given by:

1. \(\frac{B^2}{2 V E^2}\)
2. \(\frac{2 V B^2}{E^2}\)
3. \(\frac{2 V E^2}{B}\)
4. \(\frac{E^2}{2 V B^2}\)

Answer: 4. \(\frac{E^2}{2 V B^2}\)

According to the law of conservation of energy,

e V =\(\frac{1}{2} m v^2 \)

V = \(\sqrt{\frac{2 \mathrm{e} V}{m}}\)  →  Equation 1

The condition is, that the electron beam is not deflected then

⇒ \(F_m =F_e \)

⇒ \(B_e v =E_e \)

v =\(\frac{E}{B}\)  → Equation 2

From eq. (1) and (2),

⇒ \(\frac{E}{B} =\sqrt{\frac{2 \mathrm{eV}}{m}} \)

⇒ \(\frac{E^2}{B^2} =\frac{2 \mathrm{eV}}{m}\)

∴ \(\frac{e}{m} =\frac{E^2}{2 V B^2}\)

Question 24. A particle having a mass of \(10^{-2}\) kg carries a charge of 5 x \(10^{-8}\) C. The particle is given an initial horizontal velocity of \(10^5 \mathrm{~ms}^{-1}\) in the presence of an electrical field \(\vec{E}\) and magnetic field \(\vec{B}\). To keep the particle moving in a horizontal direction, it is necessary that:

1. \(\vec{B}\) should be perpendicular to the direction of velocity \(\vec{E}\) should be along the direction of velocity.

2. Both \(\vec{B}\) and \(\vec{E}\) should be along the direction of velocity.

3. Both \(\vec{B}\) and \(\vec{E}\) are mutually perpendicular and perpendicular to the direction of velocity.

4. \(\vec{B}\) should be along the direction of velocity and \(\vec{E}\) should be perpendicular to the direction of velocity.

Which one of the following pairs of statements is possible?

1. (A)(1) and (3)
2. (B)(3) and (4)
3. (2) and (3)
4. (2) and (4)

Answer: 3. (2) and (4)

Both \(\vec{B}\) and \(\vec{E}\) should be along the direction of velocity.

Both \(\vec{B}\) and \(\vec{E}\) are mutually perpendicular and perpendicular to the direction of velocity.

Question 25. A beam of electrons passes undeflected through mutually perpendicular electric and magnetic fields. If the electric field is switched off, and the same magnetic field is maintained, the electrons move:

1. in a circular orbit
2. along a parabolic path
3. along a straight line
4. in an elliptical orbit.

Answer: 1. in a circular orbit

In the magnetic field a charged particle moves in a circular orbit.

Question 26. In a mass spectrometer for measuring the masses of ions, the ions are initially accelerated by an electric potential V and then made to describe semicircular paths of radius R using a magnetic field B. If V and B are kept constant, the \(\left(\frac{\text { charge on the ion }}{\text { mass of the ion }}\right)\) will be proportional to:

1. \(\frac{1}{R^2}\)
2. \(R^2\)
3. R
4. \(\frac{1}{R}\)

Answer: 1. \(\frac{1}{R^2}\)

The radius of the semicircular path

R=\(\frac{m v}{q B}=\frac{\sqrt{2 m q V}}{q B}\)

As V and B are constant so,

R \(\propto \frac{\sqrt{m q}}{q}\)

∴ \(\frac{q}{m} \propto \frac{1}{R^2}\)

Question 27. Below are two statements:

Statement 1: Biot-Savart’s law gives us the expression for the magnetic field strength of an infinitesimal current element (M) of a current-carrying conductor only.

Statement 2: Biot-Savart’s law is analogous to Coulomb’s inverse square law of charge q, with the former being related to the field produced by a scalar source, Idl while the latter being produced by a vector source, q. In light of the above statements choose the most appropriate answer from the options given below:

1. Both Statement 1 and Statement 2 are correct.
2. Both Statement 1 and Statement 2 are incorrect.
3. Statement 1 is correct and Statement 2 is incorrect.
4. Statement 1 is incorrect and Statement 2 is correct

Answer: 3. Statement 1 is correct and Statement 2 is incorrect.

According to Biot – Savart’s law, dB=\(\frac{\mu_0(I d l \times r)}{4 \pi r^3}\)

Here, the current element Idl is a vector quantity and the coulomb’s force is produced by scalar source q. Hence statement – 1 is correct, but statement – 2 is incorrect.

Question 28. An electron is moving in a circular path under the influence of a transverse magnetic field of 3.57 x 10^-2 T. If the value of e/m is 1.76 x 10¹¹ C/kg, the frequency of revolution of the electron is:

1. 1 GHz
2. 100 MHz
3. 62.8 MHz
4. 6.28 MHz

Answer: 1. 1 GHz

Radius of charged particle in magnetic field is, r=\(\frac{m v}{q B}\)

and time taken to complete the circle

⇒ \(\mathrm{T} =\frac{2 \pi r}{V}\)

⇒ \(\frac{T}{2 \pi} =\frac{m}{q B}\)

⇒ \(\omega =\frac{2 \pi}{T}-\frac{q B}{m}\)

Here \(\mathrm{q}= e. \frac{e}{m}=1.76 \times 10^{11} \mathrm{C} / \mathrm{kg}\)

Here \(\mathrm{q}=\text { e. } \frac{e}{m}=1.76 \times 10^{11} \mathrm{C} / \mathrm{kg} \)

and \(\frac{T}{2 \pi} =\frac{e B}{m}\)

= \(\frac{1}{2 \pi} \frac{e}{m} \mathrm{~B} \)

= \(\frac{1}{2 \pi} \times 1.76 \times 10^{11} \times 3.57 \times 10^{-2} \)

= \(1.0 \times 10^9 \mathrm{~Hz}\)

= 1 \(\mathrm{GHz}\)

Question 29. A long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the center of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the center of the coil of n turns will be:

1. nB
2. n²B
3. 2nB
4. 2n²B

Answer: 2. n²B

Since, l=2\( \pi R=n(2 \pi r)\)

r=\(\frac{R}{n}\)

for one turn B=\(\frac{\mu_0 I}{2 R}\)

for n turn \(B^{\prime}=\frac{\mu_0 n I}{2 r}\)

⇒ \(B^{\prime} =\frac{\mu_0 n^2 I}{2 R}=n^2\left(\frac{\mu_0 I}{2 R}\right)\)

∴ \(B^{\prime} =n^2 B\)

Question 30. A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to the X-axis while a semicircular portion of radius R lies in the Y-Z plane. The magnetic field at point O is:

1. B=\(\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}+2 \hat{k})\)
2. B=\(\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}-2 \hat{k})\)
3. B=\(\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}+2 \hat{k})\)
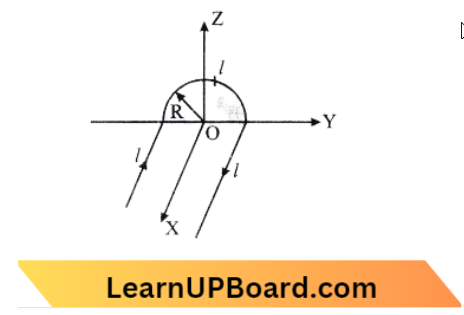
4. B=\(\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}-2 \hat{k})\)

Answer: 4. B=\(\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}-2 \hat{k})\)

Magnetic field due to wire parallel to the x-axis is, \(B_I=\frac{\mu_0}{4 \pi} \frac{I}{R}(-\hat{k})\)

Magnetic field due to another wire parallel to the x-axis is, \(B_{I I I}=\frac{\mu_0}{4 \pi} \frac{I}{R}(-\hat{k})\)

Magnetic field due to half semi-circular wire is, \(B_{I I}=\frac{\mu_0 I}{4 R}(\hat{i})\)

Magnetic field at the centre of wire is, B =\(B_I+B_{I I}+B_{I I I}\)

= \(\frac{\mu_0 I}{4 \pi R}(-2 \hat{k}+\pi \hat{i})\)

Question 31. A current loop consists of two identical semicircular parts each of radius R, one lying in the x-y plane and the other in the x-z plane. If the current in the loop is i. The resultant magnetic field due to the two semicircular parts at their common center is

1. \(\frac{\mu_0 i}{2 \sqrt{2} R}\)
2. \(\frac{\mu_0 i}{2 R}\)
3. \(\frac{\mu_0 i}{4 R}\)
4. \(\frac{\mu_0 i}{\sqrt{2 R}}\)

Answer: 1. \(\frac{\mu_0 i}{2 \sqrt{2} R}\)

The radius of the semi-circular part = R then the magnetic field

⇒ \(B_1=B_2 \frac{\mu_0 l}{4 \mathrm{R}}\)

Then magnetic field at their common center will be:

⇒ \(\vec{B} =\vec{B}_1+\vec{B}_2\)

⇒ \(|\vec{B}| =\sqrt{\left(\frac{\mu_0 i}{4 R}\right)^2+\left(\frac{\mu_0 i}{4 R}\right)^2}\)

B =\(\frac{\mu_0 i}{2 \sqrt{2} R}\)

Question 32. Two circular coils 1 and 2 are made from the same wire but the radius of the 1st coil is twice that of the 2nd coil. What potential difference in volts should be applied across them so that the magnetic field at their centers is the same?

1. 2
2. 3
3. 4
4. 6

Answer: 3. 4

Let \(r_1\) and \(r_2\) be the radius of coil 1 and coil 2. If \(B_1\) and \(B_2\) are magnetic induction at their centre then,

⇒ \(B_1=\frac{\mu_0 I_1}{2 r_1}\) and \(B_2=\frac{\mu_0 I_2}{2 r_2}\)

⇒ \(B_1=B_2\) and  \(r_1=2 r_2\) there  \(I_1=2 I_2\)

Again if \(R_1\) and \(R_2\) are resistance of the coil 2 then \(R_1=2 R_2 \)(as R \(\propto\) length =\(2 \pi r\)) and if \(V_1 and V_2\) are the potential difference across them respectively then,

⇒ \(\frac{V_1}{V_2}=\frac{I_1 R_1}{I_2 R_2} \)

= \(\frac{\left(2 I_2\right)\left(2 R_2\right)}{I_2 R_2}\)=4

Question 33. An electron moves in a circular orbit with a uniform speed v. It produces a magnetic field B at the center of the circle. The radius of the circle is proportional to

1. \(\sqrt{\frac{B}{v}}\)
2. \(\frac{B}{v}\)
3. \(\sqrt{\frac{v}{B}}\)
4. \(\frac{v}{B}\)

Answer: 3. \(\sqrt{\frac{v}{B}}\)

The magnetic field is produced by moving electrons in a circular path,

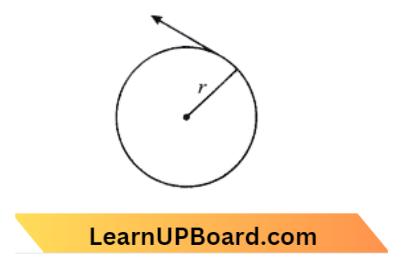
B=\(\frac{\mu_0 I}{2 r} \)

where, I=\(\frac{\rho}{t}=\frac{\rho}{2 \pi r} \times v\)

B=\(\frac{\mu_0 \rho v}{4 \pi r^2}\)

r \(\propto \sqrt{\frac{\nu}{B}} \)

Question 34. The magnetic field of a given length of wire for a single turn coil at the center is ‘B’ then, its value for two turns coil for the same wire is:

1. \(\frac{B}{4}\)
2. \(\frac{B}{2}\)
3. 4B
4. 2B

Answer: 3. 4B

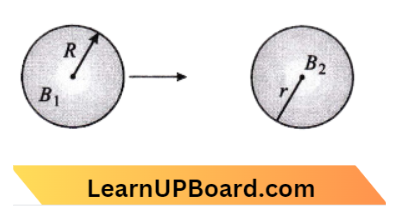
Here \(B_1 =B=\frac{\mu_0 I}{2 R}\)

⇒ \(B_2 =\frac{\mu_0(2 \mathrm{I})}{2 r}\)

2 \(\times 2 \pi r =2 \pi R \)

r =\(R / 2\)

Question 35. From Ampere’s circuital law for a long straight wire of circular cross-section carrying a steady current, the variation of the magnetic field in the inside and outside region of the wire is:

1. uniform and remains constant for both the regions
2. a linearly increasing function of distance up to the boundary of the wire and then linearly decreasing for the outside region
3. a linearly increasing function of distance r up to the boundary of the wire and then decreasing one with Hr dependence for the outside region
4. a linearly decreasing function of distance up to the boundary of the wire and then a linearly increasing one for the outside region.

Answer: 3. a linearly increasing function of distance r up to the boundary of the wire and then decreasing one with Hr dependence for the outside region

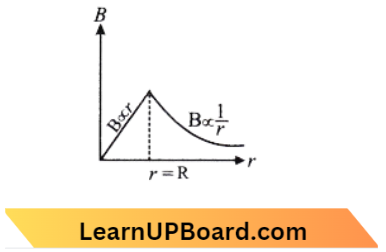
According to ampere’s circuital label, \(\mathrm{B}_{\text {in }} =\frac{\mu_0 I r}{2 \pi a^2} \text { or } \mathrm{B}_{\text {in }} \propto r\)

∴ \(\mathrm{~B}_{\text {out }} =\frac{\mu_0 I}{2 \pi r} \text { or } \mathrm{B}_{\text {out }} \propto \frac{1}{r}\)

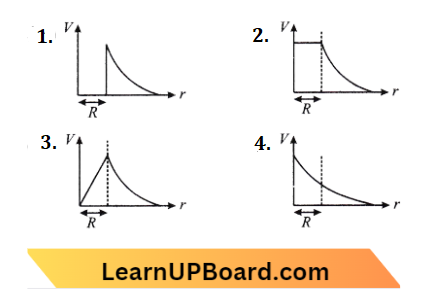
Question 36. A thick current-carrying cable of radius R’ carries current I uniformly distributed across its cross-section. The variation of magnetic field B(r) due to the cable with the distance V from the axis of the cable is represented by

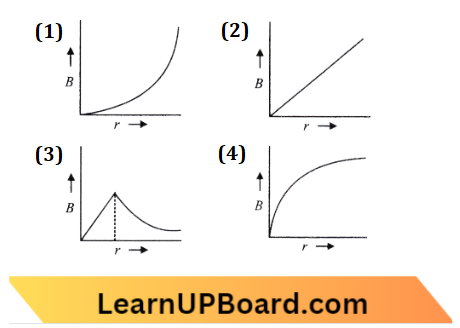
Answer: 3.

Inside the field drops linearly while outside it drops as a power of two.

Question 37. A cylindrical conductor of radius R is carrying a constant current. The plot of the magnitude of the magnetic field B with the distance d from the center of the conductor is correctly represented by the figure:

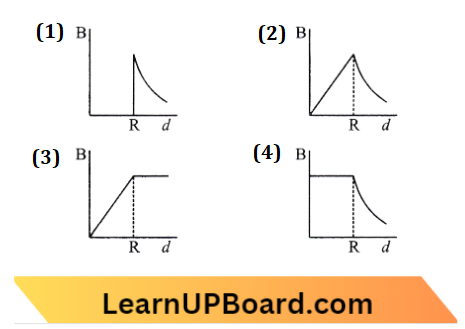
Answer: 2.

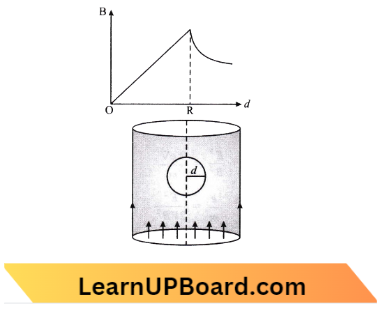
Inside \((d<R)\)

Magnetic field inside conductor,

B=\(\frac{\mu_0}{2 \pi R^2} I d\)

Or B=k d  →  Equation 1

A straight line passing through the origin, At surface (d=R)

B=\(\frac{\mu_0}{2 \pi} \frac{I}{R}\)  →  Equation 2

Maximum at surface, Outside \((d>\mathrm{R})\)

B =\(\frac{\mu_0}{2 \pi} \frac{I}{d}\)

B \(\propto \frac{I}{d} \text { (Hyperbolic) }\)

Question 38. A long straight wire of radius a carries a steady current L. The current is uniformly distributed over its cross-section. The ratio of the magnetic field B and B’ at a radial distance\(\frac{a}{2}\)and 2a respectively, from the axis of the wire is:

1. \(\frac{1}{2}\)
2. 1
3. 4
4. \(\frac{1}{4}\)

Answer: 2. 1

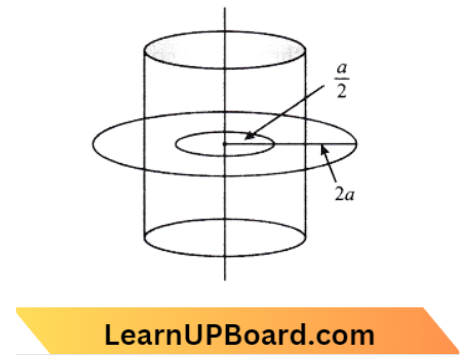
Here two Amperian loops of radius \(\ \frac {a}{2}\) and 2 a are shown from Ampere’s Circuital law

⇒ \(\oint B \cdot d L=\mu_0 I_{\text {enclosed }}\)

∴ for small loops,

\(\mathrm{B} \times 2 \pi \frac{a}{2} =\mu_0 \times \frac{\mathrm{I}}{\pi a^2} \times \pi\left(\frac{a}{2}\right)^2\)

= \(\frac{\mu_0 I}{4}\)

B =\(\frac{\mu_0 I}{4}\)  → Equation 1

Similarly for bigger loops,

⇒ \(B^{\prime} \times 2 \pi(2 a) =\mu_0 I\)

⇒ \(B^{\prime} =\frac{\mu_0 I}{4 \pi a}\)  → Equation 2

∴ \(B^{\prime} =\frac{\mu_0 I}{4 \pi a} \times \frac{4 \pi a}{\mu_0 I}\)=1

Question 39. Two identical long conducting AOB and COD are placed at right angle wires to each other with one above the other such that O is their common point for the two. The wires carry I₁ and I₂ currents respectively. Point P is lying at distance d from O along a direction perpendicular to the plane containing the wires. The magnetic field at the point P will be :

1. \(\frac{\mu_0}{2 \pi d}\left(\frac{I_1}{I_2}\right)\)
2. \(\frac{\mu_0}{2 \pi d}\left(I_1+I_2\right)\)
3. \(\frac{\mu_0}{2 \pi d}\left(I_1^2-I_2^2\right)\)
4. \(\frac{\mu_0}{2 \pi d}\left(I_1^2+I_2^2\right)\)

Answer: 4. \(\frac{\mu_0}{2 \pi d}\left(I_1^2+I_2^2\right)\)

According to the questions.

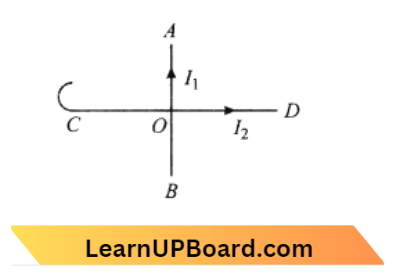
Two wires AOB and COD are placed at a right angle. O is the common point.

⇒ \(I_1\) and \(I_2\) are current flowing in the wires.

Point P is lying at distance d along the 2 -axis So

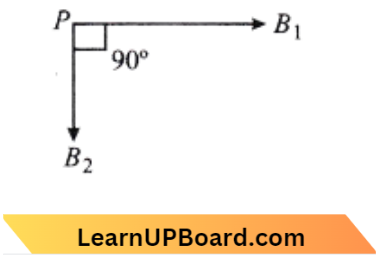
⇒ \(\left|B_1\right|=\frac{\mu_0}{2 \pi} \frac{I_1}{d} \)

⇒ \(\left|B_2\right|=\frac{\mu_0}{2 \pi} \frac{I_2}{d}\)

⇒ \(B_net =\sqrt{B_1^2+B_2^2}\)

=\(\sqrt{\left(\frac{\mu_0}{2 \pi} \times \frac{I_1}{d}\right)^2+\left(\frac{\mu_0}{2 \pi} \times \frac{I_2}{d}\right)^2}\)

=\(\frac{\mu_0}{2 \pi} \frac{\left(I_1^2+I_2^2\right)}{d}\)

Question 40. If a long hollow copper pipe carries a current, then a magnetic field is produced:

1. inside the pipe only
2. outside the pipe only
3. both inside and outside the pipe
4. nowhere

Answer: 2. outside the pipe only

According to Ampere’s circuital law,

⇒  \(\int B \cdot d I =\mu_0 I_enclosed\)

so, B\((2 \pi r) =\mu_0 \times 0 \quad\left[I_{\text {enclosed }}=0\right] \)

B =0

Since there is no current inside the Ampere’s surface

in a hollow metallic (copper) pipe, hence, the magnetic field is zero.

For external points, however, the entire current behaves as if it were concentrated along the axis.

So outside \(\tilde{B}_0=\frac{\mu_0 I}{2 \pi r}\)

Thus, the magnetic field is only created outside the pipe.

Question 41. A coil of one turn is made of a wire of a certain length and then from the same length a coil of two turns is made. If the same current is passed in both cases, then the ratio of the magnetic induction at their centers will be:

1. 2:1
2. 1:4
3. 4:1
4. 1:2

Answer: 2. 1:4

Magnetic induction at the center of a current-carrying coil with \(\mathrm{N}\) turns is equal to

⇒  \(\mathrm{B}=\frac{\mu_0 N I}{2 r}\)

Suppose the length of the wire is L.

Case 1: For coil of one turn, let radius be \(r_1\).

L =2 \(\pi r_1 \times N \)

or \(r_1=\frac{L}{2 \pi \times N}=\frac{L}{2 \pi}\) (N=1)

Case 2: For a coil of two turns, let the radius be \(r_2\).

L=2 \(\pi r_2 \times N \)

or \(r_2=\frac{L}{2 \pi \times N}=\frac{L}{2 \pi \times 2}\)( N=2)

or \(r_2=\frac{r_1}{2}\)

By comparing two different cases from Eq. (1), we get,

or \(\frac{B_1}{B_2}=\frac{N_1}{r_1} \times \frac{r_2}{N_2}\)

∴ \(\frac{B_1}{B_2}=\frac{1}{4}\)

Question 42. Two equal electric currents are flowing perpendicular to each other as shown in the figure. AB and CD are perpendicular to each other and symmetrically placed w.r.t the currents, where do we expect the resultant magnetic field to be zero?

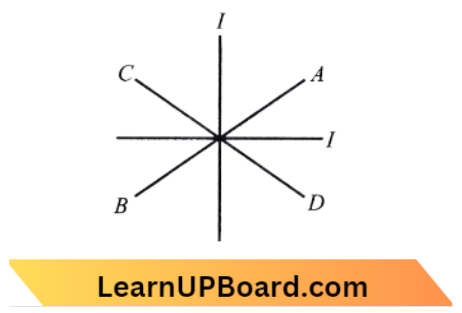
1. On AB
2. On CD
3. On both AB and CD
4. On both OD and BO

Answer: 1. On AB

Using the right-hand grip rule and considering AB, the magnetic field corresponding to one current is upwards and the magnetic field due to the other is downwards. Both magnetic fields cancel each other out, and the resultant magnetic field is zero. When considering CD and applying the right-hand grip rule to the two currents, the magnetic field direction is the same in both cases, resulting in a non-zero resultant.

Question 43. A straight wire of diameter 0.5 mm carrying a current of 1 A is replaced by another wire of 1mm diameter carrying the same current. The strength of the magnetic field far away is:

1. twice the earlier value
2. same as the earlier value
3. one-half of the earlier value
4. one-quarter of the earlier value

Answer: 2. same as the earlier value

Magnetic field due to straight wire, B=\(\frac{\mu_0}{4 \pi} \frac{2 i}{r}\)

The magnetic field due to a current-carrying conductor does not depend on the diameter of the wire; it only depends on the distance of the wire from the point and the current in the wire, therefore the magnetic field for both wires remains the same.

Question 44. A long solenoid of radius 1 mm has 100 turns per mm. If 1 A current flower in the solenoid, the magnetic field strength at the center of the solenoid is:

1. 6.28 x 10^-2 T
2. 12.56 x 10^-2 T
3. 12.56 x 10^-4 T
4. 6.28 x 10^-4 T

Answer:  2. 12.56 x 10^-2 T

Given: \(\mathrm{I}=1 A, n=\frac{100}{1 \mathrm{~mm}}=100 \times 10^3 \mathrm{~m}\)

The magnetic field strength at the center of the solenoid,

⇒ \(\mathrm{B} =\mu_0 n I\)

=4 \(\pi \times 10^{-7} \times 10^5 \times 1\)

=12.56 \(\times 10^{-2} \mathrm{~T}\)

Question 45. A long solenoid of 50 cm in length having 100 turns carries a current of 2.5 A. The magnetic field at the center of the solenoid is (Take, μ₀ = 4π  x 10^-7 T m A^-1):

1. 3.14 x 10^-4T
2. 6.28 x 10^-5T
3. 3.14 x 10^-5T
4. 6.28 x 10^-4T

Answer: 4. 6.28 x 10^-4T

From the question, l=50 \(\mathrm{~cm}=0.5 \mathrm{~m}\), N=100 turns and I=2.5 \(\mathrm{~A}\)

Magnetic field at the centre of solenoid is M =\(\mu_{\mathrm{o}} n I=\mu_{\mathrm{o}}\left(\frac{\mathrm{N}}{t}\right) I\)

= 4 \(\pi \times 10^{-7} \times \frac{100}{0.5} \times 2.5 \)

= 6.28 \(\times 10^{-4} \mathrm{~T}\)

Question 46. Two toroids 1 and 2 have a total number of turns 200 and 100 respectively with average radii of 40 cm and 20 cm respectively. If they cany’ the same current I, the ratio of the magnetic field along the two loops is :

1. 1:1
2. 4: 1
3. 2: 1
4. 1: 2

Answer: 1. 1:1

We know that the magnetic field within the turns of the toroid is :

⇒ \(\mathrm{B} =\mu_0 n I \)

=\(\mu_0\left(\frac{N}{l}\right) I=\frac{\mu_0 N I}{2 \pi R}\)

Where, N= No. of turns

I= Current in loop

R= radius of each turn

⇒ \(\frac{B_1}{B_2}=\frac{\frac{N_1}{R_1}}{\frac{N_2}{R_2}}\)

Because is same =\(\frac{\frac{200}{40}}{\frac{100}{20}}=\frac{5}{5}\)=1: 1

Question 47. A long solenoid of diameter 0.1 m has 2 x 10⁴turns per meter. At the center of the solenoid, a coil of 100 turns and a radius of 0.01 m is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate of 0 A from 4 A in 0.5 s. If the resistance of the coil is 10 μ²Ω, the total charge flowing through the coil during this time is:

1. 32π μC
2. 16 μC
3. 32 μC
4. 16π μC

Answer: 3. 32 pC

From the question, Resistance of the solenoid R=10 \(\pi^2 \Omega\)

Radius of second coil \(\boldsymbol{r}=10^{-2}\)

⇒ \(\Delta t=0.05 \mathrm{~s}, \Delta i=4-0=4 \mathrm{~s}\)

Then we know that the charge flowing through the coil is,

⇒ \(\Delta q= (\frac{\Delta \phi}{\Delta t}) \frac{1}{R} \times(\Delta t)\)

= \(\mu_0 N_1 N_2 \pi r^2\left(\frac{\Delta 1}{\Delta t}\right) \frac{1}{R} \Delta t\)

= 4 \(\pi \times 10^{-7} \times 2 \times 10^4 \times 100 \times \pi\)

⇒ \(\times\left(10^{-2}\right)^2 \times\left(\frac{4}{0.05}\right) \times \frac{1}{10 \pi^2} \times 0.05 \)

= 32 \(\times 10^{-6} \mathrm{C}=32 \mu \mathrm{C}\)

Question 48. An arrangement of three parallel straight wires placed perpendicular to the plane of paper carrying the same current I along the same direction is shown in the figure. The magnitude of force unit length on the middle wire B is given by:

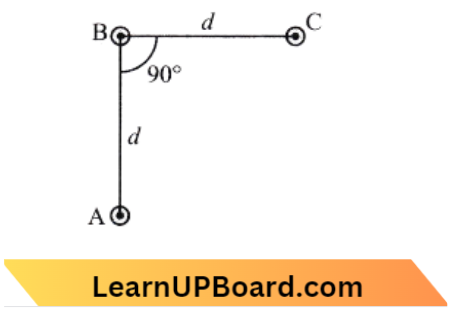
1. \(\frac{\mu_0 I^2}{2 \pi d}\)
2. \(\frac{2 \mu_0 I^2}{\pi d}\)
3. \(\frac{\sqrt{2} \mu_0 I^2}{\pi d}\)
4. \(\frac{\mu_0 I^2}{\sqrt{2} \pi d}\)

Answer: 4. \(\frac{\mu_0 I^2}{\sqrt{2} \pi d}\)

The force between BC and AC will be the same in magnitude,

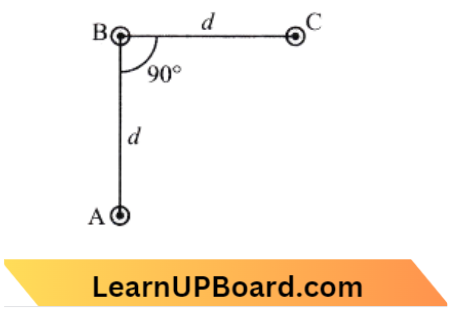
⇒ \(F_{B C}=F_{B A}=\frac{\mu_0 I^2}{2 \pi d}\)

and Resultant force on B,

F=\(\sqrt{F_1^2+F_2^2}\)

F=\(\sqrt{2} F_{B C}=\sqrt{2} \frac{\mu_0 I^2}{2 \pi d}\)

F=\(\frac{\mu_0 I^2}{\sqrt{2} \pi d}\)

Question 49. A square loop ABCD carrying a current I, is placed near and coplanar with a straight conductor XY carrying a current I, the net force on the loop will be:

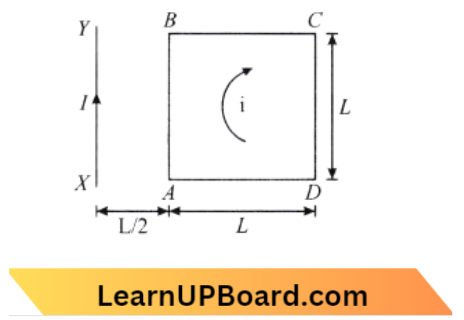
1. \(\frac{\mu_0 I i}{2 \pi}\)
2. \(\frac{2 \mu_0 I i \mathrm{~L}}{3 \pi}\)
3. \(\frac{\mu_0 I i \mathrm{~L}}{2 \pi}\)
4. \(\frac{2 \mu_0 I i}{3 \pi}\)

Answer: 4. \(\frac{2 \mu_0 I i}{3 \pi}\)

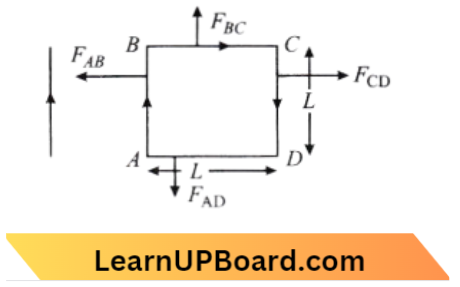
⇒ \(F_{A B}=I l B\) (attraction)

⇒ \(F_{A B}=\frac{\mu_0 l i(L)}{2 \pi(L / 2)}=\frac{\mu_0 l i}{\pi}\)

⇒ \(F_{B C}=(\uparrow) and F_{A D}(\downarrow)\)

Cancels each other, \(F_{C D}=I l B\) (Repulsion)

⇒ \(\mathrm{F}_{\mathrm{CD}} =\frac{\mu_0 I i(L)}{2 \pi(3 L / 2)}=\frac{\mu_0 l i}{3 \pi}\)

∴ \(F_{\text {net }} =\frac{\mu_0 I i}{\pi}\left(1-\frac{1}{3}\right)=\frac{2 \mu_0 l i}{3 \pi}\)

Question 50. A square loop carrying a steady I is placed in a horizontal plane near a long straight conductor carrying a steady current I₁ at a distance cl from the conductor as shown in the figure, the loop will experience:

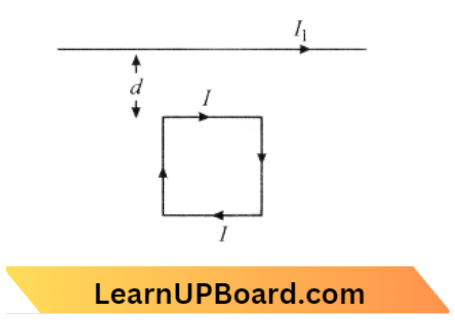
1. a net repulsive force away from the conductor
2. a net torque acting upward perpendicular to the horizontal plane
3. a net torque acting downward normal to the horizontal plane
4. a net attractive force toward the conductor

Answer: 4. a net attractive force toward the conductor

The situation is shown in the diagram,

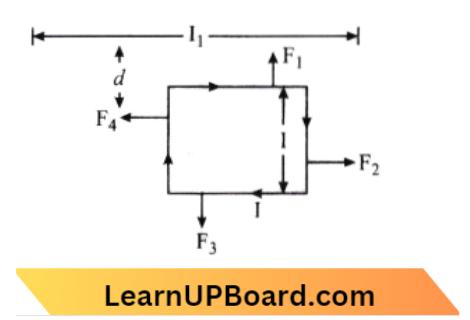
The relation between\( F_2\) and\( F_4\) is,

⇒ \(F_2 =-F_4\)

⇒ \(F_1 =\frac{\mu_0 \mathrm{I}_1 l}{2 \pi d}\)

⇒ \(F_2 =\frac{\mu_0 \mathrm{I}_1 l}{2 \pi(d+1)}\)

⇒ \(F_1 >F_3\)

⇒ \(F_net =F_1-F_3\)

So the wire attracts a loop.

Question 51. A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of the magnetic field is:

1. \(\frac{B}{2}\)
2. B
3. 2 B
4. 4 B

Answer: 2. B

Magnetic field induction at point insides the solenoid of length l, having n turns per unit length carrying current i. is given by B=\(\mu_0 n I\)

If 1 is double and n is halved then B remains the same.

Question 52. A uniform conducting wire of length 12a and resistance ‘R’ is wound up as a current-carrying coil in the shape of:

(1) an equilateral triangle of side ‘a’

(2) a square of side ‘a’

The magnetic dipole moments of the coil in each case respectively are:

1. \(\sqrt{3} \mathrm{I} a^2\) and 3 \(\mathrm{I}^2\)
2. 3\( \mathrm{I} a^2\) and \(\mathrm{I} a^2\)
3. 3 \(\mathrm{I} a^2\) and 4 \(\mathrm{I} a^2\)
4. 4 \(\mathrm{I}^2\) and 3 \(\mathrm{I} a^2\)

Answer: 1. \(\sqrt{3} \mathrm{I} a^2\) and 3 \(\mathrm{I}^2\)

Given the length of wire l=12 a

Resistance =\(\mathrm{R} \)

Current =\(\mathrm{I}\)

(1) Equilateral triangle of side a

m= ?

(2) Square of side ‘as we know, m=\(\mathrm{NI} A\)

Triangle, \(\mathrm{A}=\frac{\sqrt{3}}{4} a^2\)

Perimeter =3 \(\mathrm{a}\)

⇒ \(\mathrm{N}\) =4

m =4. I.\(\frac{\sqrt{3}}{4} a^2 \)

= \(\sqrt{3} \mathrm{I} a^2\)

Square \(\mathrm{A} =a^2\)

Perimeter =4 \(\mathrm{a} \)

⇒ \(\mathrm{N}\) =3

m= 3 \(\mathrm{I} a^2 \)

∴ \(\sqrt{3} I a^2, 3 I a^2\)

Question 53. A wire of length L carrying a current of I ampere is bent in the form of a circle. Its magnetic moment is:

1. \(\frac{\mathrm{IL}^2}{4}\)
2. \(\frac{\mathrm{I} \pi \mathrm{L}^2}{4}\)
3. \(\frac{2 \mathrm{IL}^2}{\pi}\)
4. \(\frac{\mathrm{IL}^2}{4 \pi}\)

Answer: 4. \(\frac{\mathrm{IL}^2}{4 \pi}\)

When a wire of length L is bent in the form of a circle of radius \(R_1\) then,

L=\(2 \pi R\)

R=\(\frac{L}{2 \pi} \)

Magnetic moment, \(\mu=1 \mathrm{~A}\)

= I\(\left(\pi R^2\right) \)

= I \(\cdot \pi \cdot\left(\frac{L}{2 \pi}\right)^2\)

= \(\frac{I \pi L^2}{4 \pi^2}=\frac{I L^2}{4 \pi}\)

Question 54. A 250-turn rectangular coil of length 2.1 cm and width 1.25 cm carries a current of 85 μA and is subjected to a magnetic field of strength 0.85T. Work done for rotating the coil by 180° against the torque is:

1. 9.5 μ
2. 4.55 μ
3. 2.3 μ
4. 1.5μ

Answer: 1. 9.5 μ

Work done for rotating the coil

W =M B\(\left(\cos \theta_1-\cos \theta_2\right)\)

W =M B\(\left(\cos 0^{\circ}-\cos 180^{\circ}\right)\)

= 2 M B=\(2 \times N I A \times B \)

= 2 \(\times 250 \times 85 \times 10^{-6} \times 2.1\)

= 9.48 \(\times 10^{-6} \mathrm{~J}\)

= 9.5 \(\mu \mathrm{J}\)

Question 55. A rectangular coil of length 0.12 m and width 0.1 m having 50 turns of wire is suspended vertically in a uniform magnetic field of strength 0.2 Wb/m². The coil carries a current of 2 A. If the plane of the coil is. inclined at an angle of 30° with the direction of the field, the torque required to keep the coil in stable equilibrium will be:

1. 0.15 Nm
2. 0.20 Nm
3. 0.24 Nm
4. 0.12 Nm

Answer: 2. 0.20 Nm

According to the question,

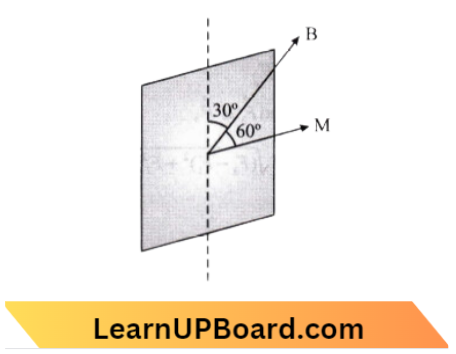
Magnetic field strength, B=0.2 \(\mathrm{~Wb} / \mathrm{m}^2\)

Number of turns, N=50, \(\theta=60^{\circ}\)

A=0.12\( \times 0.1=0.012 \mathrm{~m}^2\)

Then Torque, \(\tau =N l A B \sin \theta\)

= 50 \(\times 2 \times 0.012 \times 0.2 \times \sin 60^{\circ} \)

= 50 \(\times 2 \times 0.12 \times 0.2 \times \frac{\sqrt{3}}{2} \)

= 0.20 \(\mathrm{Nm}\)

Question 56. A current loop in a magnetic field:

1. experiences a torque whether the field is uniform or non-uniform in all orientation
2. can be in equilibrium in one orientation
3. can be equilibrium in two orientations
4. can be in equilibrium in two orientations are stable  while the other is unstable

Answer: 4. can be in equilibrium in two orientations are stable  while the other is unstable

For parallel is stable and for antiparallel is unstable.

Question 57. A circular Coil ABCD carrying a current i is placed in a uniform magnetic field, if the magnetic force on the segment AB is \(\vec{F}\), the force on the remaining segment BCDA is:

1. \(-\vec{F}\)
2. 3 \(\vec{F}\)
3. \(-3 \vec{F}\)
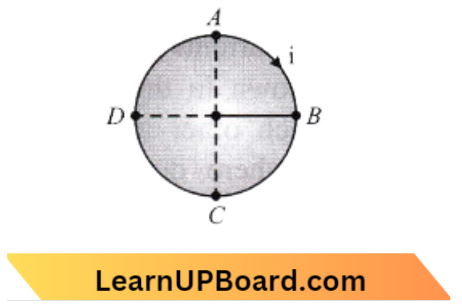
4. \(\vec{F}\)

Answer: 1. \(-\vec{F}\)

The net magnetic force on a current loop in a uniform magnetic field is always zero.

⇒ \({\mathrm{F}}_{\mathrm{AB}}+\overrightarrow{\mathrm{F}}_{\mathrm{BCAD}}\) =0

∴ \(\overrightarrow{\mathrm{F}}_{\mathrm{BCAD}}+-\overrightarrow{\mathrm{F}}_{\mathrm{AB}} =-\overrightarrow{\mathrm{F}}\)

Question 58. A square current-carrying loop is suspended in a uniform magnetic field acting in the plane of the loop. If the force on one arm of the loop is \(\vec{F}\) :

1. \(3 \vec{F}\)
2. –\(\vec{F}\)
3. –\(\overrightarrow{3 F}\)
4. \(\vec{F}\)

Answer: 2. –\(\vec{F}\)

If magnetic field B is uniform then force on closed path = 0

One force is l⁷ then we want to give the total force as zero.

This confirms that, \(\vec{F}=-\vec{F}\) for zero net force

Question 59. A closely wound solenoid of 2000 turns and area of cross-section 1.5 x \(10^{-4} \mathrm{~m}^2\) carries a current of 2.0 A. It is suspended through its center and perpendicular to its length, allowing it to turn in a horizontal plane in a uniform magnetic field \(5 \times 10^{-2}\) T making an angle of 30° with the axis of the solenoid, the torque on the solenoid will be:

1. \(3 \times 10^{-3} \mathrm{~N}-\mathrm{m}\)
2. 1.5 \(\times 10^{-3} \mathrm{~N}-\mathrm{m}\)
3. 1.5 \(\times 10^{-2} \mathrm{~N}-\mathrm{m}\)
4. 3 \(\times 10^{-2} \mathrm{~N}-\mathrm{m}\)

Answer: 3. 1.5 \(\times 10^{-2} \mathrm{~N}-\mathrm{m}\)

From the question, N=2000 \(\mathrm{~A}, A=1.5 \times 10^{-4} \mathrm{~m}^2\)

I=2 \(\mathrm{~A}, B=5 \times 10^{-2} \mathrm{~T}, \theta=30^{\circ} \)

Torque, \(\tau =N I B A \sin \theta\)

=2000 \(\times 2 \times 5 \times 10^{-2} \times 1.5 \times 10^{-4} \times \sin 30^{\circ}\)

=2000 \(\times 50 \times 10^{-6} \times \frac{1}{2}\)

=1.5 \(\times 10^{-2} \mathrm{Nm}\)

Question 60. A closed-loop PQRS carrying a current is placed in a uniform magnetic field. If the magnetic forces on segments PS, SR, and RQ are \(F_1, F_2\) and \(F_3\) respectively, and are in the plane of the paper and along the directions shown, the force on the segment QP is:

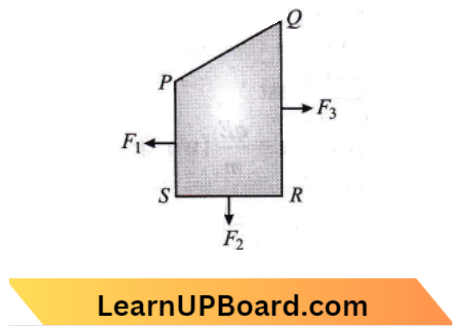
1. \(F_3-F_1-F_2\)
2. \(\sqrt{\left(F_3-F_1\right)^2+F_2^2}\)
3. \(\sqrt{\left(F_3-F_1\right)^2-F_2^2}\)
4. \(F_3-F_1+F_2\)

Answer: 2. \(\sqrt{\left(F_3-F_1\right)^2+F_2^2}\)

The total force on the current carrying closed loop should be zero. If placed in a uniform magnetic field.

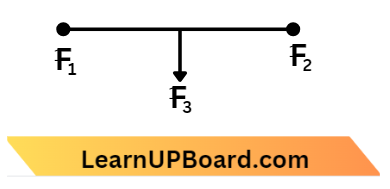
⇒ \(F_{\text {horizontal }} =F_3-F_1\)

⇒ \(\mathrm{~F}_{\text {vertical }} =F_2\)

Resultant of \(\vec{F}_1, \vec{F}_2 and \vec{F}_3 is \vec{F},\)

Where, \(\vec{F}=\sqrt{\left(F_3-F_1\right)^2+F_2^2}\)

since total force =0,

Hence force on QP is equal to \(\vec{F}\) in magnitude but opposite direction

∴ \(F_{\mathrm{QP}}=\sqrt{\left(F_3-F_1\right)^2+F_2^2}\)

Question 61. A charged particle (charge q) is moving in a circle of radius R with uniform speed v. The associated magnetic moment p is given by:

1. \(q v R^2\)
2. \(q v R^2 / 2\)
3. qvR
4. qvR / 2.

Answer: 4. \(q v R^2\)

Magnetic moment \(\mu\)=I A

Since, T=\(\frac{2 \pi R}{v}\)

also, I=\(\frac{q}{T}=\frac{q v}{2 \pi R}\)

⇒ \(\mu =\left(\frac{q v}{2 \pi R}\right)\left(\pi R^2\right)\)

= \(\frac{q v R}{2}\)

Question 62. A current-carrying coil is subjected to a uniform magnetic field. The coil will orient so that its plane becomes:

1. inclined at 45° to the magnetic field
2. inclined at any arbitrary angle to the magnetic field
3. parallel to the magnetic field
4. perpendicular to the magnetic field

Answer: 3. parallel to the magnetic field

The coil must be oriented in such a way that its magnetic moment coincides with the field. so that the coil’s magnetic force is zero.

Question 63. The current sensitivity of a moving coil galvanometer is 5 div/mA and its voltage sensitivity (angular deflection per unit voltage applied) is 20 div/V. The resistance of the galvanometer is:

1. 250 Ω
2. 25 Ω
3. 40 Ω
4. 500 Ω

Answer: 1. 250 Ω

Current sensitivity \(\left(\mathrm{I}_{\mathrm{S}}\right)\) for moving coil galvanometer is:

⇒ \(I_S=\frac{\theta}{I}=\frac{N A B}{C}\) →   Equation 1

Where, N = Number of turns in the coil

A = Area of each turn of the coil

B = Magnetic field

C = Restoring torque per unit twist of the stip

Again, voltage sensitivity \((V_S)\) is given by,

⇒ \(V_S =\frac{\theta}{V}=\frac{N A B}{C R_G}\)  → Equation 2

⇒ \(R_G\) = resistance of galvanometer

Resistance of galvanometer is, \(R_G=\frac{I_S}{V_s}=\frac{5 \times 1}{20 \times 10^{-3}}=\frac{5000}{20}=250 \Omega\)

∴ \(R_G=250 \Omega\)

Question 64. In the ammeter, 0.2% of the main current passes through the galvanometer. If the resistance of the galvanometer is G, the resistance of the ammeter will be:

1. \(\frac{1}{499}\) G
2. \(\frac{499}{500}\) G
3. \(\frac{1}{500}\) G
4. \(\frac{500}{499}\) G

Answer: 1. \(\frac{1}{499}\) G

The situation of the question is given below,

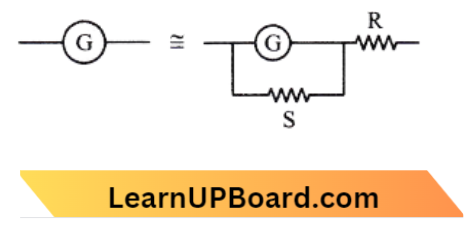
For ammeter, \(\mathrm{G} \times 0.002 l =0.998 l \times r_g\)

∴ –\(\ r_g =\frac{0.002}{0.998} \mathrm{G}=\frac{1}{499} \mathrm{G}\)

Question 65. A millivoltmeter of 25 mV range is to be converted into an ammeter of 25 A range. The value (in ohm) of the necessary shunt will be:

1. 0.001
2. 0.01
3. 1
4. 0.05

Answer: 1. 0.001

Deflection current \(\mathrm{I}_g=\frac{25 m v}{G} ampere\)

Where, \(\mathrm{G}\)= resistance of meter

The value of the shunt will be,

S= \(\frac{I_g G}{I-I_g}=\frac{25 M V}{25}=0.001 \Omega\)

Question 66. A galvanometer of resistance, G is shunted by a resistance S ohm. To keep the main current in the circuit unchanged, the resistance to be put in series with the galvanometer is:

1. \(\frac{S^2}{(S+G)}\)
2. \(\frac{S G}{(S+G)}\)
3. \(\frac{G^2}{(\mathrm{~S}+G)}\)
4. \(\frac{G}{(S+G)}\)

Answer: 3. \(\frac{G^2}{(\mathrm{~S}+G)}\)

According to the question,

If resistance is the same then the current is unchanged

G = \(\frac{G S}{G+S}+R \)

R = \(G-\frac{G-S}{G+S}\)

= \(\frac{G^2}{G+S}\)

Question 67. A galvanometer has a coil of resistance 100 Ω and gives a full-scale deflection for 30 mA current. If it is to work as a voltmeter in the 30 V range, the resistance required to be added will be:

1. 900 Ω
2. 1800 Ω
3. 500 Ω
4. 1000 Q

Answer: 1. 900 Ω

Required resistance, R =\(\frac{V}{i_g}-G=900 \mathrm{~W}\)

=\(\frac{30}{30 \times 10^{-3}}-100=900 \Omega\)

Question 68. A galvanometer having a coil resistance of 60 Ω shows full-scale deflection when a current of 1.0 A passes through it. It can be converted into an ammeter to read currents up to 5.0 A by:

1. putting in parallel a resistance of 240 Ω
2. putting in series a resistance of 15 Ω
3. putting in series a resistance of 240 Ω
4. putting in parallel a resistance of 15 Ω

Answer: 4. putting in parallel a resistance of 15 Ω

From the question,

Given, \(G_1=60 \Omega, \mathrm{I}_{\mathrm{g}}=1.0 \mathrm{~A}, \mathrm{I}=5 \mathrm{~A}\)

⇒ \(\mathrm{I}_{\mathrm{g}} G=\left(I-I_{\mathrm{g}}\right) S\)

S=\(\frac{I_g G}{I-I_{\mathrm{g}}}=\frac{1}{5-1} \times 60=15 \Omega\)

Question 69. A galvanometer of resistance 50 Ω connected to a battery of 3 V along with a resistance of 2950 Ω. in series. A full-scale deflection of 30 divisions is obtained in the galvanometer. To reduce this deflection is 20 divisions order to reduce this deflection to 20 divisions, the resistance series should be:

1. 5050 Ω
2. 5550 Ω
3. 6050 Ω
4. 4450 Ω

Answer: 4. 4450 Ω

Current through a galvanometer,

I=\(\frac{3 V}{50 \Omega+2950 \Omega}=10^{-3} \mathrm{~A}\)

Current for 30 division =\(10^{-3} \mathrm{~A}\)

= \(\frac{20}{30} \times 10^{-3}\)

= \(\frac{2}{3} \times 10^{-3} \mathrm{~A}\)

= \(\frac{3}{50+R}\)

R=4450 \(\Omega\)

Question 70. The resistance of an ammeter is 13 Ω and its scale is graduated for a current up to 100 amps. After an additional shunt has been connected to this ammeter it becomes possible to measure currents up to 750 amperes by this meter. The value of shunt-resistance is:

1. 2 Ω
2. 0.2 Ω
3. 2 k Ω
4. 20 Ω

Answer: 1. 2 Ω

Let S= shunt resistance

Given that, I=750 \(\mathrm{~A}\)

⇒ \(I_g=100 \mathrm{~A}, R_G=13 \Omega\)

from the figure, \(I_g R_G =\left(I-I_g\right) S \)

100 \(\times 13 =[750-100] S\)

S =2 \(\Omega\)

Question 71. A galvanometer acting as a voltmeter will have:

1. a high resistance in parallel with its coil
2. a high resistance in series with its coil
3. low resistance in parallel with its coil
4. a coil resistance in series with its coil

Answer: 2. a high resistance in series with its coil

A galvanometer acting as a voltmeter will have a high resistance in series with its coil.

Question 72. A galvanometer of 50 ohm resistance has 25 divisions. A current 4 x 10^-4 ampere gives a deflection of one division. To convert this galvanometer into a voltmeter having a range of 25 volts, it should be connected with a resistance of:

1. 2500 Ω as a shunt
2. 2450 Ω as a shunt
3. 2550 Ω in series
4. 2450 Ω in series

Answer: 4. 2450 Ω in series

Total current in the galvanometer,

⇒ \(I_g=25 \times 4 \times 10^{-4} \mathrm{~A}\)

⇒ \(I_g=10^{-2} \mathrm{~A}\)

The value of resistance connected in series to convert a galvanometer into a voltmeter of 25 \(\mathrm{~V}\) is

R =\(\frac{V}{I_g}-G \)

= \(\frac{25}{10^{-2}}-50 \)

= 2450 \(\Omega\)

Question 73. To convert a galvanometer into a voltmeter one should connect a:

1. high resistance in series with the galvanometer
2. low resistance in series with the galvanometer
3. high resistance in parallel with the galvanometer
4. low resistance in parallel with the galvanometer

Answer: 1. High resistance in series with the galvanometer

To convert a galvanometer into a voltmeter one should connect a high resistance in series with galvanometer.

Current Electricity

Question 1. A steady current of 1.5 amp flows through a copper voltameter for 10 minutes. If the electrochemical equivalent of copper is 30 x 10⁵ g coulomb^-1, the mass of copper deposited on the electrode will be:

1. 0.50 g
2. 0.67 g
3. 0.27 g
4. 0.40 g.

Answer: 4. 0.40 g

Given that, I = 1.5A, t= 10 min = 600 sec

and z=30 \(\times 10^{-5} \mathrm{~g} \) coulomb \( ^{-1}\)

According to faraday first law of electrolysis, m=Z I T=30 \(\times 10^{-5} \times 1.5 \times 600=0.27 \mathrm{~g}\)

Question 2. Two have solid same conductor length and are the same made resistance. up of sameOnematerialof them and has 1 volt a circular cross-section of the area \(A_1\) and the other one has a square cross-section of area \(A_2\). The ratio \(\frac{A_1}{A_2}\)is :

1. 1.5
2. 1
3. 0.8
4. 2

Answer: 2. 1

From question, \(R_1=R_2\) and \(l_1=l_2\) Hence, Resistance, R=\(\rho \frac{l}{A}\)

⇒ \(\frac{R_1}{R_2}=\frac{l_1}{l_2} \cdot \frac{A_2}{A_1}\)

⇒ \(\frac{R_1}{R_2}=\frac{l_1}{l_2} \cdot \frac{A_2}{A_1}\)

∴ \({A_2}/{A_1}\)=1 .

Question 3. The resistance of a wire is R ohm. If it is melted and stretched to n times its original length, its new resistance will be:

1. nR
2. \(\frac{R}{n}\)
3. \(n^2 R\)
4.  \(v\frac{R}{n^2}\)

Answer: 1. nR

In both cases the volume of material is the same, \(A_1 l_1=A_2 l_2\)

It is also given, \(l_2=n l_1\)

⇒ \(A_1 l_1=A_2 n l_1\)

⇒ \(A_2 =\frac{A_1}{n}\)

Now when the wire is stretched the resistance

⇒ \(R_1=\rho \frac{l_1}{A_2}=\rho \cdot \frac{n l_1}{\frac{A_1}{n}}\)

∴ \( R_1=R \boldsymbol{n}^2 [\text { Since } R=(\rho \frac{l_1}{A_2})]\)

Read and Learn More NEET Physics MCQs

Question 4. A wire of resistance 4 Ω is selected to twice its original length. The resistance of a stretched wire would be:

1. 2 Ω
2. 4 Ω
3. 8 Ω
4. 16 Ω

Answer: 4. 16 Ω

R=\(\frac{\rho l}{A}=4 \Omega\)

New length i’= 2i

on stretching volume remains constant

Resistance of stretched wire is,

⇒ \(\mathrm{R}^{\prime} =\frac{\rho l^{\prime}}{A^{\prime}}=f \frac{(2 l)}{(A / 2)}=\frac{4 \rho l}{A}\)

= 4 \(\times 4=16 \Omega\)

Question 5. A wire of a certain material is stretched slowly by ten percent. It’s new resistance and specific resistance become respectively:

1. 1.2 times, 1.1 times
2. 1.21 times, same
3. both remain the same
4. 1.1 time, 1.1 times

Answer: 2. 1.21 times, same

After stretching, specific resistance (\( \rho \)) will remain the same.

Original resistance of the wire

or \(\mathrm{R}=\rho \frac{l}{A}\)

or \(\mathrm{R} \propto \frac{l}{A}\)

and \(\mathrm{R} \propto \frac{l^2}{V} (as V=Al) \)

⇒ \(\frac{R^{\prime}}{R}=\frac{\left(l+\frac{10}{100} l\right)^2}{l^2}\)

⇒ \(\frac{R^{\prime}}{R} =\frac{\left(\frac{11}{10} l\right)^2}{l^2}=\frac{121}{100}\)

∴ \(R^{\prime}\) =1.21 R

Question 6. The electric resistance of a certain wire of iron is R. If its length and radius are both doubled, then:

1. the resistance will be doubled and the specific resistance will be halved
2. the resistance will be halved and the specific resistance will remain unchanged
3. the resistance will be halved and the specific resistance will be doubled
4. the resistance and the specific resistance, both will remain unchanged

Answer: 2. the resistance will be halved and the specific resistance will remain unchanged

Resistance of wire R=\(\rho \frac{l}{A}\)

Means R \(\propto \frac{l}{A}=\frac{l}{\pi r^2}\)

According to the question when l and R are doubled

⇒ \(R_1 \propto \frac{2 l}{\pi(2 r)^2}\)

⇒ \(R_1 \propto \frac{1}{2} R\)

Here specific resistance of the wire is independent of the geometry wire so it depends on the material of the wire.

Question 7. A 6-volt battery is connected to the terminal of a three-metre-long wire of uniform thickness and resistance of 100 ohms. The difference of potential between two points on the wire separated by a distance of 50 cm will be:

1. 2 volt
2. 3 volt
3. 1 volt
4. 1.5 volt

Answer: 3. 1 volt

Voltage on 50 cm =\(\frac{6}{300} \times 50\)

=1 volt

Question 8. There are three copper wires of length and cross-sectional area (2 L, A/2) (1/2, 2 A). In which case is the resistance minimum?

1. It is the same in all three cases
2. Wire of cross-sectional area 2 A
3. Wire of cross-sectional area A
4. Wire of cross-sectional area A

Answer: 2. Wire of cross-sectional area 2 A

The relation between the length and cross-section area of a wire is given by, \(\mathrm{R}=\frac{\rho I}{A}\)  → Equation 1

where, \(\rho\) specific resistance. It is the proportionality constant and depends on the nature of the material.

(1) Length =\(\frac{L}{2}\),

cross-sectional area =2 \(\mathrm{~A}\)

Putting in Eq. (1), we get

∴ \(\mathrm{R}=\frac{\rho(\mathrm{L} / 2)}{2 A}=\frac{\rho L}{4 A}\)

(2)Length =L, cross-sectional area =A

Putting in (1), we get

∴ \(\mathrm{R}=\frac{\rho L}{A}\)

(3)Length =2 L, cross-sectional area =\(\frac{A}{2}\)

Putting in (1), we get

⇒ \(\mathrm{R}=\rho \frac{2 L}{A / 2}=\frac{4 \rho L}{A}\)

It is clear from above, that resistance is minimum only in option(B).

Question 9. If a negligibly small current is passed through a wire of length 15 m and of resistance \(5 \Omega\) having the uniform cross-section of \(6 \times 10^{-7} \mathrm{~m}^2\), then coefficient of resistivity of the material, is

1. 1 \(\times 10^{-7} \Omega-\mathrm{m}\)
2. 2 \(\times 10^{-7} \Omega-\mathrm{m}\)
3. 3 \(\times 10^{-7} \Omega-\mathrm{m}\)
4. 4 \(\times 10^{-7} \Omega-\mathrm{m}\)

Answer: 2. 2 \(\times 10^{-7} \Omega-\mathrm{m}\)

Given, l =15 \(\mathrm{~m}\)

A = 6 \(\times 10^{-7} \mathrm{~m}^2\)

R = 5 \(\Omega, \rho\)=?

We have, \(\rho =\frac{R A}{l} \)

= \(\frac{5 \times 6 \times 10^{-7}}{15} \)

= 2 \(\times 10^{-7} \Omega-\mathrm{m}\)

Question 10. A copper wire of length 10m and radius \(\left(\frac{10^{-2}}{\sqrt{\pi}}\right) m\) has an electrical resistance of \(10 \pi\). The current density in the wire for an electric field strength of 10 (v/m) is:

1. \(104 \mathrm{~A} / \mathrm{m}^2\)
2. 106 \(\mathrm{~A} / \mathrm{m}^2\)
3. 10-5 \(\mathrm{~A} / \mathrm{m}^2\)
4. 105 \(\mathrm{~A} / \mathrm{m}^2\)

Answer: 4. 105 \(\mathrm{~A} / \mathrm{m}^2\)

Given, R=10 \(\Omega, E=10 \mathrm{v} / \mathrm{m}, l=10 \mathrm{~m}\)

Radius, r=\(\frac{10^{-2}}{\sqrt{\pi}} m\)

We know, \(\rho =\frac{R A}{l}=\frac{10 \times \pi \times \frac{10^{-4}}{\sqrt{\pi}}}{10}\)

= \(10^{-4} \pi \mathrm{m}\)

Current density, J=E \(\sigma=\frac{E}{\rho}=\frac{10}{10^{-4}}=10^5 \mathrm{~A} / \mathrm{m}^2\)

Question 11. Column 1 gives certain physical terms associated with the flow of current through a metallic conductor.
Column 2 gives some mathematical relations involving electrical quantities. Match Column-1 and Column-2 with appropriate relating

1. (A)-(3), (B)-(4), (C)-(1), (D)-(5)
2. (A)-(3), (B)-(4), (C)-(2), (D)-(4)
3. (A)-(3), (B)-(1), (C)-(4), (D)-(2)
4. (A)-(3), (B)-(2), (C)-(4), (D)-(1)

Answer: 1. (A)-(3), (B)-(4), (C)-(1), (D)-(5)

Drift velocity, \(\mathrm{v}_d=\frac{e E}{m} \tau\)

Current density, \(\mathrm{J}=\frac{I}{A}=\frac{n e A v_d}{A}=n e v_d\)

Resistivity, \(\rho=\frac{m}{n e^2 \tau}\)

⇒ \(\tau=\frac{m}{n e^2 \rho}\)

Resistance, \(\mathrm{R}=\mathrm{V} / \mathrm{I}\)

⇒ \(\rho \frac{l}{\mathrm{~A}}=\frac{\mathrm{E} l}{\mathrm{I}}\)

∴ \(\rho=\frac{\mathrm{E}}{\mathrm{I}}\)

Question 12. In a potentiometer circuit, a cell of EMF 1.5V gives a balance point at 36 cm length of wire. If another cell of EMF 2.5 V replaces the first cell, then at what length of the wire, the balance point occur?

1. 60 cm
2. 21.6 cm
3. 64 cm
4. 62 cm

Answer: 1. 60 cm

Given,\(\varepsilon_1=1.5 \mathrm{~V}\)

Balance length, \( l_1 =36 \mathrm{~cm}\)

⇒  \(\varepsilon_2 =2.5 \mathrm{~V}\)

⇒  \(l_2\) =?

We know, \(\varepsilon=\phi l\)

⇒ \(\frac{\varepsilon_1}{\varepsilon_2}=\frac{l_1}{l_2} \)

⇒ \(l_2=\frac{\varepsilon_2 l_1}{\varepsilon_1}=\frac{2.5 \times 36}{1.5}\)

∴ \(-l_2=36 \times \frac{5}{3}=60 \mathrm{~cm}\)

Question 13. Across a metallic conductor of a non-uniform cross-section, a constant potential difference is applied. The quantity which remains constant along the conductor is:

1. current density
2. current
3. drift velocity
4. electric field

Answer: 2. current

We know that, Current density, j=\(\frac{I}{A}\)  → Equation 1

Drift velocity \(v_d=\frac{I}{n A_e}=\frac{j}{n e}\) →  Equation 2

Electric field, E=\(\rho j\) →  Equation 3

From eq. (1), (2) and (3) we confirm that current density, drift velocity, and electric field depend on the area of the conductor.

Even if the area of the cross-section of the conductor is nonuniform, the number of electrons flowing

Question 14. The resistance of a discharge tube is:

1. zero
2. ohmic
3. non-ohmic
4. infinity

Answer: 3. non-ohmic

In a discharge tube, the flow of positive ions and electrons causes the current. Moreover, secondary electron emission is possible. As a result of the nonlinearity of the V-I curve, its resistance will be nonohmic.

Question 15. From the graph between current I and voltage V shown in the figure, identify the portion corresponding to negative resistance.

1. DE
2. BC
3. CD
4. AB

Answer: 2. BC

From Ohm’s law,R=\(\frac{\Delta V}{\Delta I}\)

If current decreases as voltage or temperature rises, then resistance is said to be negative.

In the V-I graph, The current drops with rising voltage in graph segment CD.

Thus, The negative resistance is represented by portion CD.

Question 16. The color code of resistance is given below: The values of resistance and tolerance respectively, are:

1. \(47 \mathrm{k} \Omega, 10 \%\)
2. 4.7 \(\mathrm{k} \Omega, 5 \%\)
3. 470 \(\mathrm{k} \Omega, 5 \%\)
4. 470 \(\mathrm{k} \Omega, 10 \%\)

Answer: 3. 470 \(\mathrm{k} \Omega, 5 \%\)

From the color code of carbon resistors

Code of yellow = 4

Code of violet = 7

Code of brown =\(10^1(multiples)\)

Code of gold = \(\pm 5 \% (tolerance)\)

Hence resistance of resistor =47 \(\times 10^1 \Omega \pm 5 \%\)

=470 \(\Omega \pm 5 \%\)

Question 17. A carbon resistor of (47 ± 4.7) k\(\Omega\). is to be marked with rings of different colors for its identification. The color code sequence will be:

1. Yellow – Green – Violet – Gold
2. Yellow – Violet – Orange – Silver
3. Violet – Yellow – Orange – Silver
4. – Green – Orange – Violet – Gold

Answer: 2. Yellow – Violet – Orange – Silver

Seeing the table we confirm the color assigned to a number

4 → Yellow

7 → Violet

3 → Orange

and 10% accuracy says about the color of silver.

Hence the color code sequence will be yellow, violet, orange, and silver.

Question 18. As the temperature increases, the electrical resistance:

1. increase for both conductors and semiconductors.
2. decrease for both conductors and semiconductors.
3. increase for conductors but a decrease for semiconductors
4. decrease for conductors but increase for semiconductors

Answer: 3. increase for conductors but a decrease for semiconductors

Increase for conductors but decrease for semiconductors.

As the temperature increases, the resistance of the conductor increases, and for semiconductors decreases, because the temperature coefficient of resistance \((\propto)\) is positive for conductors and negative for insulators.

Question 19. The solids which have the negative temperature coefficient of resistance are:

1. insulator only
2. semiconductor only
3. insulators and semiconductors
4. metals

Answer: 3. insulators and semiconductors

The negative temperature coefficient of the resistance is only present in the insulators or the semiconductors. In, these, the resistance decreases with an increase in temperature.

Question 20. Which of the following graphs represents the variation of resistivity (p) with temperature (7) for copper?

Answer: 2.

For copper at 0 \(\mathrm{~K} \), the value of resistivity is 1.7 \(\times 10^{-8} \Omega \mathrm{m}\).

Question 21. The specific resistance of a conductor increases with the:

1. increase in the temperature
2. increase in the cross-section area
3. increase in the cross-section and decrease in the length
4. increase in the cross-section area

Answer: 1. increase in the temperature

The specific resistance of conduction increases with increases in the temperature.

Question 22. Two resistors of resistance, 100 Ω, and 200Ω, are connected in parallel in an electrical circuit. The ratio of the thermal energy developed in 100 Ω to that in 200Ω in a given time is:

1. 1: 2
2. 2: 1
3. 1: 4
4. 4: 1

Answer: 2. 2: 1

We know, \(\mathrm{H}=\frac{V^2}{R} t\)

so,\(\mathrm{H}_1=\frac{V^2}{100} t\)

⇒ \(\mathrm{H}_2=\frac{V^2}{200} t\)

so,\(\frac{\mathrm{H}_1}{\mathrm{H}_2}=\frac{200}{100}\)=2: 1

Question 23. Which of the following acts as a circuit protection device?

1. Inductor
2. Switch
3. Fuse
4. Conductor

Answer: 3. Fuse

Equipment, machinery components, and devices in electrical and electronic circuits against short circuits, over-currents, and earth faults are called protective devices.

Protective devices are necessary to protect electrical appliances or equipment.

From the given devices fuse is used in electric circuits as a protective device, it helps prevent excessive amounts of current from flowing in the circuit or from short-circuiting.

Question 24. A filament bulb (500 W, 100 V) is to be used in a 230 V main supply. When a resistance R is connected in series, it works perfectly and the bulb consumes 500 W. The value of R is:

1. 230 Ω
2. 46 Ω
3. 26 Ω
4. 13 Ω.

Answer: 3. 26 Ω

Current through bulb, \(\mathrm{I}=\frac{P}{V}=\frac{500 \mathrm{~W}}{100 \mathrm{~V}}\)

R =\(\frac{130 \mathrm{~V}}{5 \mathrm{~V}}=26 \Omega\)

Question 25. The two cities are 150 km apart. Electric power is sent from one city to another city through copper wires. The fall of potential per km is 8 V and the average resistance per km is 0.5 Q. The power loss in the wire is:

1. 19.2 W
2. 19.2 kW
3. 19.2 J
4. 12.2 kW

Answer: 2. 19.2 kW

Given the potential difference between the two cities

V =8 \(\times 150=1200 \mathrm{~V}\)

Average resistance =0.5 \(\times 150=75 \Omega\)

Power loss, \(\mathrm{P} =\frac{V^2}{R}=\frac{1200 \times 1200}{75}\)

=19200 W

=192 kW

Question 26. If the voltage across a bulb rated 220 V, 100 W drops by 2.5% to its rated value the percentage at the rated value by which the power would decrease is its:

1. 20%
2. 2.5%
3. 5%
4. 10%

Answer: 3. 5%

We know power, \(\mathrm{P}=\frac{V^2}{R}\)

⇒ \(\frac{\Delta P}{P} \times 100 \% =\frac{2 \Delta P}{V} \times 100 \%\)

=2.25=5 %

Question 27. In producing chlorine by electrolysis 100 kW power at 125 V is being consumed. How much chlorine per minute is liberated (ECE of chlorine is 0.367 x 10^-6 kgC^-1).

1. 1.76 x 10-3 kg
2. 9.67 x 10-3 kg
3. 17.61 x 10-3 kg
4. 3.67 x 10-3 kg

Answer: 1. 1.76 x 10-3 kg

According to the question, Mass of the substance deposited at the cathode, m = ZIt

= Z\(\left(\frac{P}{V}\right)\) t

= 0.367 \(\times 10^{-6} \times \frac{100 \times 10^3}{125} \times 60\)

= 17.6 \(\times 10^{-3} \mathrm{~kg}\)

Question 28. A cell can be balanced against 110 cm and 100 cm of potentiometer wire, respectively with and without being short-circuited through a resistance of 10 Ω. Its internal resistance is:

1. 1.0Ω
2. 0.5Ω
3. 2.0 Ω
4. zero

Answer: 1. 1.0 Ω

In a potentiometer experiment, when we find the internal resistance of a cell. Let E be the emf of the cell and V the potential difference. Then

⇒ \(\frac{E}{V}=\frac{l_1}{l_2}[l_1 and l_2 \) are length of wire ]Since \(\frac{E}{V}=\frac{R+r}{R}[E=I(R+r) an V=\mathrm{I} R]\)

⇒ \(\frac{R+r}{R} =\frac{l_1}{l_2}\)

⇒ \(1+\frac{r}{R} =\frac{110}{100} \)

⇒ \(\frac{r}{R} =\frac{10}{100}\)

r=\(\frac{1}{10} \times 10=1 \Omega\)

Question 29. The total power dissipated in watts in the circuit shown here is:

1. 40
2. 54
3. 4
4. 16

Answer: 2. 54

Total power dissipated, \(\mathrm{P}=\frac{V^2}{R}\)

= \(\frac{18 \times 18}{6}=54 \mathrm{~W}\)

Question 30. In producing chlorine through electrolysis 100 watt power at 125 V is being consumed. How much chlorine per minute is liberated? E. C. E. of chlorine is 0.367 x 10^-6kg/coulomb:

1. 13.6 mg
2. 17.6 mg
3. 21.3 mg
4. 24.3 mg

Answer: 2. 17.6 mg

P=100 \(\mathrm{~W}, V=125 \mathrm{~V}\)

P=V I

-I=\(\frac{P}{V}=\frac{100}{125} \mathrm{~A}\)

Mass of chlorine liberated =2 \(\mathrm{It}\)

= 0.367 \(\times 10^{-6} \times \frac{100}{125} \times 60 \)

= 0.0176 \(\times 10^{-3} \mathrm{~kg}\)

=17.6 \(\mathrm{mg}\)

Question 31. A 5-ampere fuse wire can withstand a maximum power of 1 watt in the circuit. The resistance of the fuse wire is:

1. 0.04 ohm
2. 0.2 ohm
3. 5 ohm
4. 0.4 ohm

Answer: 1. 0.04 ohm

P =\(I^2 R \)

I =\(25 \times R\)

R =\(\frac{1}{25}=0.04 \Omega\)

Question 32. When three identical bulbs of 60-watt, 200-volt rating are connected in series to a 200-volt supply, the power drawn by them will be:

1. 60 watt
2. 180 watt
3. 10 watt
4. 20 watt

Answer: 4. 20 watt

The resistance of each bulb is \(\frac{V^2}{P}=\frac{(200)^2}{60} \Omega\) when three bulbs are connected in series then equivalent resistance is, \(\frac{3 \times(200)^2}{60}\).

Power,P=\(\frac{V^2}{R_{e q}}=20 \mathrm{~W}\).

Question 33. In India electricity is supplied for domestic use at 220 V. It is supplied at 110 V in the USA. If the resistance of a 60 W bulb for use in India is R, the resistance of a 60 W bulb for use in the USA will be:

1. \(\mathrm{R}\)
2. 2 \(\mathrm{R}\)
3. \(\frac{R}{4}\)
4. \(\frac{R}{2}\)

Answer: 3. \(\frac{R}{4}\)

In India, \(P_1=\frac{(220)^2}{R}\)

In USA \(P_V=\frac{(110)^2}{R_0}\)

As \(P_1=P_V\)

⇒ \(\frac{(220)^2}{R}=\frac{(110)^2}{R_V}\)

⇒ \(R_v=\frac{110 \times 110}{220 \times 220}\)

∴ \(R_v=\frac{R}{4}\)

Question 34. A fuse wire is a wire of:

1. high resistance and high melting point
2. high resistance and low melting point
3. low resistance and low melting point
4. low resistance and high melting point

Answer: 2. high resistance and low melting point

Fuse wire must have high resistance (per unit length) and low melting point.

Question 35. Two bulbs 25 W, 22 V, and 100 W, 220 V are given. Which has higher resistance?

1. 25 W bulb
2. 100 W bulb
3. Both bulbs have equal resistance
4. The resistance of bulbs cannot be compared

Answer: 1. 25 W bulb

We have, power of electric bulb, P=\(\frac{V^2}{R}\)

R=\(\frac{V^2}{P}\)

For the same potential difference V,

R \(\propto \frac{1}{P}\)

As a result, we can see that when power is low, resistance is high, and vice versa.

Given,\(P_1=25 \mathrm{~W}, P_2=100 \mathrm{~W}\),

⇒ \(V_1=V_2=220 \mathrm{~V}\)

∴ Hence, the resistance of 25 \(\mathrm{~W}\) bulb is maximum and 100 \mathrm{W} bulb is minimum.

Question 36. A current of 2 A, passing through a conductor produces 80 J of heat in 10 s. The resistance of the conductor in the ohm is:

1. 0.5
2. 2
3. 4
4. 20

Answer: 2. c

The work done in carrying a charge q from one end to the other end of a conductor with the potential difference V equals the amount of heat created in that conductor.

⇒ \(H=W=V q=V i t=i^2 R t\) [Since, V=I R ]

H=\(i^2 R t J \)

R=\(\frac{H}{\left(i^2 t\right)}\)

Given, H=80 \(\mathrm{~J}, i=2 \mathrm{~A}, t=10 \mathrm{~s}\),

So,R=\(\frac{80}{(2)^2 \times 10}=2 \Omega\)

Question 37. The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section, and the same material is 0.25 \(\Omega\). What will be the effective resistance if they are connected in series?

1. \(0.25 \Omega\)
2. 0.5 \(\Omega \)
3. 1 \(\Omega \)
4. 4 \(\Omega\)

Answer: 4. 4 \(\Omega\)

Given, Parallel connection,

No. of wires =4

Length =l

Area = A is the same

Material =f is the same

⇒ \(\mathrm{R}_{\text {eff }} =0.25 \Omega\)

⇒ \(\mathrm{R}_{\mathrm{S}}\) =?

⇒ \(\mathrm{R}_{\mathrm{P}} =\frac{\mathrm{R}}{n}=\frac{\mathrm{R}}{4}\)

= 0.25

⇒ \(\mathrm{R}=1 \Omega\)

∴ \(\mathrm{R}_{\mathrm{S}}=n \mathrm{R}=4 \mathrm{R}=4 \Omega\)

Question 38. Three resistors having resistances \(r_1, r_2, r_3\) are connected as shown in the given circuit. The ratio \(\frac{i_3}{i_1}\) of currents in terms of resistances used in the circuit is:

1. \(\frac{r_1}{r_2+r_3}\)
2. \(\frac{r_2}{r_2+r_3}\)
3. \(\frac{r_1}{r_1+r_2}\)
4. \(\frac{r_2}{r_1+r_3}\)

Answer: 2. \(\frac{r_2}{r_2+r_3}\)

Given, \(\frac{l_3}{i_1}\)= ?

we know,\( i_1=i_2+i_3\)

and \(i_2 r_2 =i_3 r_3 \)

⇒ \(i_2 =i_1-i_3\)

⇒ \(\left(i_1-i_3\right) r_2 =i_3 r_3 \)

⇒ \(i_1 r_2 =i_3\left(r_2+r_3\right) \)

∴ \(\frac{i_3}{i_1} =\frac{r_2}{r_2+r_3}\)

Question 39. The equivalent resistance between A and B for the mesh shown in the figure is:

1. 72 W
2. 16 W
3. 30 W
4. 4.8 W

Answer: 2. 16 W

Now 4 \(\Omega, 4 \Omega and 8 \Omega\) are in series.

So, \(R_5=4 \Omega+4 \Omega+8 \Omega=16 \Omega\)

Question 40. In the circuit shown below, the reading of voltmeters and the ammeters will be:

1. \(V_1=V_2\) and \(i_1>i_2\)
2. \(\mathrm{V}_1=\mathrm{V}_2\) and \(\mathrm{i}_1=\mathrm{i}_2\)
3. \(\mathrm{V}_2=\mathrm{V}_1\) and \(\mathrm{i}_1>\mathrm{i}_2\)
4. \(\mathrm{V}_1=\mathrm{V}_2\) and \(\mathrm{i}_1=\mathrm{i}_2\)

Answer: 2. \(\mathrm{V}_1=\mathrm{V}_2\) and \(\mathrm{i}_1=\mathrm{i}_2\)

For an ideal voltmeter, resistance is infinite and for the ideal ammeter, resistance is zero.

⇒ \(V_1=i_1 \times 10=\frac{10}{10} \times 10=10 \text { volt }\)

⇒ \(V_2=i_2 \times 10=\frac{10}{10} \times 10=10 \text { volt }\)

⇒ \(V_1=V_2\)

∴ \(i_1=i_2=\frac{10 \mathrm{~V}}{10 \Omega}=1 \mathrm{~A}\)

Question 41. The reading of an ideal voltmeter in the circuit shown is

1. 0.6 V
2. 0 V
3. 0.5 V
4. 0.4 V

Answer: 4. 0.4 V

Current in A P B=\(\frac{2}{50} \mathrm{~A}\)

Current in A Q B=\(\frac{2}{50} \mathrm{~A}\)

⇒ \(\Delta \mathrm{V}\) from A to P,

⇒ \(V_{\mathrm{A}}=\frac{2}{50} \times 200=V_{\mathrm{P}}\)

⇒ \(\Delta\) V from A to Q,

⇒ \(V_{\mathrm{A}} =\frac{2}{50} \times 30=V_{\mathrm{Q}}\)

⇒ \(V_{\mathrm{P}}+\frac{2}{50} \times 20 =V_{\mathrm{Q}}+\frac{2}{50} \times 30\)

∴ \(V_{\mathrm{P}}-V_{\mathrm{Q}} =0.4 \mathrm{~V}\)

Question 42. A, B, and C are voltmeters of resistance R, 1.5 R, and 3 R respectively as shown in the figure. When some potential difference is applied between X and Y, the voltmeter readings are \(V_A, V_B, and V_C \) respectively.

1. \(V_A=V_B=V_C\)
2. \(V_A \neq V_B+V_C\)
3. \(\mathrm{V}_{\mathrm{A}}=\mathrm{V}_{\mathrm{B}} \neq \mathrm{V}_{\mathrm{C}}\)
4. \(\mathrm{V}_{\mathrm{A}} \neq \mathrm{V}_{\mathrm{B}} \neq \mathrm{V}_{\mathrm{C}}\)

Answer: 1. \(V_A=V_B=V_C\)

As in the figure, resistance \(R_B\) and \(R_C\) of the voltmeter are in parallel. So their equivalent resistance \(R^{\prime} \) is,

⇒ \(\frac{1}{R^{\prime}} =\frac{1}{R_B}+\frac{1}{R_C}\)

⇒ \(\frac{1}{R^{\prime}} =\frac{1}{1.5 R}+\frac{1}{3 R} \)

⇒ \(\frac{1}{R^{\prime}} =\frac{2+1}{3 R}\)

⇒ \(R^{\prime}\) =R

So the voltage across \(X P is V_{X P}\),

= \(V_A=I R\)

Voltage across P Q is \(V_{P Q}\),

= \(V_B=V_C=I R \)

∴ \(V_A =V_B=V_C\)

Question 43. Two metal wires of identical dimensions are connected in series. If \(\sigma_1\) and \(\sigma_2\) are the conductivities of the metal wires respectively, the effective conductivity of the combination is:

1. \(\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}\)
2. \(\frac{\sigma_1+\sigma_2}{2 \sigma_1 \sigma_2}\)
3. \(\frac{\sigma_1+\sigma_2}{\sigma_1 \sigma_2}\)
4. \(\frac{\sigma_1 \sigma_2}{\sigma_1+\sigma_2}\)

Answer: 1. \(\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}\)

From question, \(\rho =\text { resistivity }\)

A =\(\text { Area of cross-section }\)

⇒ \(R_1 =\rho_1 \frac{l}{A} \)

⇒ \(R_2 =\rho_2 \frac{l}{A}\)

and \(R_2=\rho_2 \frac{l}{A}\)

Net effective resistance, \(R_{e q} =R_1+R_2 \)

⇒ \(\rho \frac{2 l}{A} =\rho_1 \frac{l}{A}+\rho_2 \frac{l}{A}\)

∴ \(2 \rho =\rho_1+\rho_2\)

Now conductivity =\(\frac{1}{\text { resistivity }}=\frac{1}{\rho}\)

⇒ \(\frac{2}{\sigma} =\frac{1}{\sigma_1}+\frac{1}{\sigma_2}\)

⇒ \(\frac{2}{\sigma} =\frac{\sigma_1+\sigma_2}{\sigma_1 \sigma_2} \)

⇒ \(\sigma =\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}\)

The net effective conductivity of combined wire is,

∴ \(\sigma=\frac{2 \sigma_1 \sigma_2}{\sigma_1+\sigma_2}\)

Question 44. A circuit contains an ammeter, a battery of 30 V, and a resistance of 40.8 Ω all connected in series. If the ammeter has a coil of resistance 480 Ω and a shunt of 20 Ω, then the reading in the ammeter will be:

1. 0.5 A
2. 0.25 A
3. 2 A
4. 1A

Answer: 1. 0.5 A

The situation is shown in the diagram. Now effective resistance of the circuit is,

⇒ \(R_{e f f}=40.8+\frac{480 \times 20}{480+20}\)

Current, I=\(\frac{V}{R}=\frac{30}{60}=\frac{1}{2}=0.5 \mathrm{~A}\)

Reading of ampere =0.5 \(\mathrm{~A}\)

Question 45. Two rods are joined to the end, as shown. Both have a cross-sectional area of 0.01 cm2. Each is 1 meter long. One rod is of copper with a resistivity of 17 x 10^-6 ohm- centimeter, the other is of iron with a resistivity of 10⁵ ohm centimeter. How much voltage is required to produce a current of 1 ampere in the rods?

1. 0.00145 V
2. 0.0145 V
3. 1.7 x 10^-6 V
4. 0.117 V

Answer: 4. 0.117 V

According to the question, the length of each rod, l = 1 m

Area of cross-section of each rod , \(\mathrm{A}=0.01 \mathrm{~cm}^2=0.01 \times 10^{-4} \mathrm{~m}^2\)

If \(\rho_{c u}\)= resistivity of copper and \(\rho_{c u}\) is resistivity of iron then,

⇒ \(\rho_{c u}=1.7 \times 10^{-6} \Omega \mathrm{cm}=1.7 \times 10^{-8} \Omega \)

⇒ \(\rho_{f e}=10^{-5} \Omega \mathrm{cm}=10^{-7} \Omega\)

New Resistance of \(\mathrm{Cu}\) rod,

⇒ \(\mathrm{R}_{c u}=\rho_{c u} \frac{l}{A}\)

and Resistance of iron rod, \(\rho_{f e}=\rho_{f e} \frac{l}{A}\)

Both are connected in series the equivalent resistance is,

⇒ \(R_{e s} =R_{c e}+R_{F e}\)

= \(\rho_{c u} \frac{l}{\mathrm{~A}}+\rho_{f e} \frac{l}{\mathrm{~A}}=\frac{l}{\mathrm{~A}} t(\rho_{c u}+\rho_{f e}) \)

V = I R { where } I=1 \(\mathrm{~A}\} \)

= I \(\left(R_{c u}+R_{f e}\right)\)

= \(1\left(\rho_{c u}+\rho_{f e}\right) l \)

= \(\left(\rho_{c u}+\rho_{f e}\right)\left(\frac{l}{\mathrm{~A}}\right) \)

= \(\left(1.7 \times 10^8+10^{-7}\right) \times\left(\frac{1}{0.01 \times 10^{-4}}\right)\)

= \(10^{-7}(0.17+1)\left(10^6\right) \)

= 1.17 \(\times 10^{-1} \mathrm{~V} \)

= 0.117 \(\mathrm{~V}\)

Question 46. A 12 cm wire is given the shape of a right-angled triangle ABC having sides 3 cm, 4 cm, and 5 cm as shown in the figure. The resistance between two ends (AB, BC, CA) of the respective sides is measured one by one by a multi¬meter. The resistance will be in the ratio:

1. 9 : 16: 25
2. 27 :32: 35
3. 21 : 24: 25
4. 3 : 4: 5

Answer: 2. 27:32: 35

Resistance of side A B=\(R_1=\frac{3 \rho}{\mathrm{A}}\)

Resistance of side B C=\(R_2=\frac{4 \rho}{\mathrm{A}}\)

Resistance of side A C=\(R_3=\frac{5 \rho}{\mathrm{A}}\)

(Where A= Area of cross-section and \(\rho\)= resistivity of wire)

The resistance between A and B is, \(\mathrm{R}_{\mathrm{AB}} =\frac{R_1\left(R_2+R_3\right)}{R_1+R_2+R_3}\)

= \(\frac{\frac{3 \rho}{A}\left(\frac{4 \rho}{A}+\frac{5 \rho}{A}\right)}{\frac{3 \rho}{A}+\frac{4 \rho}{A}+\frac{5 \rho}{A}}=\frac{27 \rho}{12 A}\)

Similarly \(R_{B C}=\frac{R_2\left(R_1+R_3\right)}{R_1+R_2+R_3}\)

= \(\frac{\frac{4 \rho}{A}\left(\frac{3 \rho}{A}+\frac{5 \rho}{A}\right)}{\frac{3 \rho}{A}+\frac{4 \rho}{A}+\frac{5 \rho}{A}}=\frac{32}{12} \frac{\rho}{A}\)

And \(R_{A C}=\frac{R_3\left(R_1+R_2\right)}{R_1+R_2+R_3}\)

= \(\frac{\frac{5 \rho}{A}\left(\frac{3 \rho}{A}+\frac{3 \rho}{A}\right)}{\frac{5 \rho}{A}+\frac{3 \rho}{A}+\frac{4 \rho}{A}}=\frac{35}{12} \frac{\rho}{A}\)

⇒ \(R_{A B}: R_{B C}: R_{A C} =\frac{27}{12}: \frac{32}{12}: \frac{35}{12}\)

=27: 32: 35

Question 47. The power dissipated in the circuit shown in the figure is 30 watts. The value of R is

1. 20 Ω.
2. 15 Ω
3. 10 Ω.
4. 30 Ω

Answer: 3. 10 Ω.

According to the question, R_1=R

⇒ \(R_2=5 \Omega, V=10 \mathrm{~V}, P=30 \mathrm{~W}\)

P=\(\frac{V_2}{R_1}+\frac{V_2}{R_2} \)

⇒ \(\frac{10^2}{\mathrm{R}}=30-\frac{10^2}{5}\)

⇒ \(\frac{100}{R}\)=30-20

∴ \(\mathrm{R}=10 \Omega\)

Question 48. If power dissipated in the 9Ω resistor in the circuit shown is 36 W, the potential difference across the 2 Ω resistor is:

1. 8 V
2. 10 V
3. 2 V
4. 4 V

Answer: 2. 10 V

We know that power, P=\(I^2 R\)

I=\(\sqrt{\frac{P}{R}}\)

for resistance of 9 \(\Omega\),

⇒ \(I_1 =\sqrt{\frac{36}{9}} \)

= \(\sqrt{4}=2 \mathrm{~A}\)

⇒ \(I_2 =\frac{I_1 \times R}{6}=\frac{2 \times 9}{6}=3 \mathrm{~A}\)

⇒ \(I_1 =I_1+I_2=2 \mathrm{~A}+3 \mathrm{~A}=5 \mathrm{~A}\)

∴ \(V_2 =I R_2=5 \times 2=10 \mathrm{~V}\)

Question 49. A current of 3 A flows through the 2Ω resistor shown in the circuit. The power dissipated in the 5 Ω is:

1. 4 W
2. 2W
3. 1W
4. 5W

Answer: 4. 5W

Voltage across all three branches are same.

Voltage across 2 \(\Omega\) resistance,

V=2 \(\times 3=6 \mathrm{~V}\)

So voltage across lowest arm, \(V_1=6 \mathrm{~V}\) Current across\(5 \Omega\) is,

I=\(\frac{6}{1+5}=1 \mathrm{~A}\)

Power across 5 \(\Omega\) is,

P=\(I^2 R=(1)^2 \times 5=5 \mathrm{~W}\)

Question 50. In the circuit shown, the current through the 4 Ω resistor is 1 A when the point P and M are connected to a DC voltage source. The potential difference the points M and A is:

1. 1.5V
2. 1.0 V
3. 1.0V
4. 3.2 V

Answer: 4. 3.2 V

⇒ \(i_1=1 \mathrm{amp}\)= current through 4 \(\Omega\)

⇒ \(i_2\)=current through 3 \(\Omega\)

⇒ \(\frac{i_2}{i_2}=\frac{3}{4}\)

⇒ \(i_2=\frac{4}{3} \)

⇒ \(i_3=i_1+i_2=1+\frac{4}{3}=\frac{7}{3} \text { amp }\)

and \( \frac{i_3}{i_4}=\frac{3 / 4}{12 / 7} \)

⇒ \(\frac{7}{3} \times \frac{12}{7}=i_4 \times \frac{5}{4}\)

⇒ \(i_4 =\frac{16}{5}=3.2 \mathrm{amp}\)

⇒ \(\mathrm{V}_{\mathrm{NM}} \)={ P.D. across } M and N

= \(i_4 \times 1 \mathrm{~W}\)

= \(3.2 \times 1=3.2 \mathrm{Volt}\)

Question 51. Power dissipated across the 8 Ω, resistor in the circuit shown here is 2 watt. The power dissipated in watt units across the 3 Ω resistor is:

1. 3.0 W
2. 2.0 W
3. 1.0W
4. 0.5 W

Answer: 1. 3.0 W

1 \(\Omega\) and 3 \(\Omega\) are in, series so,

⇒ \(R_s=R_1+R_2\)

⇒ \(R_s=3+1=4 \Omega\)

and \(R_2=8 \Omega\)

i= current in the circuit

Current through \(R_1\) is,

⇒ \(i_1=\frac{i \times R_2}{R_1+R_2}=\frac{i \times 8}{12}=\frac{21}{3}\)

Current through \(R_2\) is,

⇒ \(i_2=\frac{1 \times R_1}{R_1+R_2}=\frac{i \times 4}{12}=\frac{i \times 8}{12}\)

Power dissipated in 3 \(\Omega\) resistance is,

⇒ \(P_1=i_1^2 \times 3\)  → Equation 1

Power dissipated in 8 \(\Omega\) resistance is:

\(P_2=i_2{ }^2 \times 8\) → Equation 2

For (1) and (2)

⇒ \(\frac{P_1}{P_2}=\frac{i_1^2 \times 3}{i_2^2 \times 8} \)

⇒ \(\frac{P_1}{P_2}=\frac{\left(\frac{2 i}{3}\right)^2 \times 3}{\left(\frac{i}{3}\right)^2 \times 8}=\frac{3}{2}\)

∴ \(P_1=\frac{3}{2} \times P_2=\frac{3}{2} \times 2=3 \mathrm{~W}\)

Question 52. When a wire of uniform cross-section a, length l, and resistance R is into a complete circle, the resistance between any two diametrically opposite points will be:

1. \(\frac{R}{4}\)
2. 4 \(\mathrm{R}\)
3. \(\frac{R}{8}\)
4. \(\frac{R}{2}\)

Answer: 1. \(\frac{R}{4}\)

\(\frac{1}{R} =\frac{2}{R}+\frac{2}{R}=\frac{4}{R}\)

∴ \(R^{\prime} =\frac{R}{4}\)

Question 53. Five equal resistance each of resistance R are connected as shown in the figure. A battery of V volts is connected between A and B. The current flowing in AFCEF will be:

1. \(\frac{3 V}{R}\)
2. \(\frac{V}{R}\)
3. \(\frac{V}{2 R}\)
4. \(\frac{2 V}{R}\)

Answer: 3. \(\frac{V}{2 R}\)

Given circuit can be reduced to,

Required current, I=\(\frac{V}{2 R}\)

Question 54. Two 220-volt, 100-watt bulbs are connected first in series and then in parallel. Each time combination is connected to a 220-volt a.c. supply line. The power drawn by the combination in each case respectively will be:

1. 50 watt, 10 watt
2. 100 watt, 50 watt
3. 200 watt, 150 watt
4. 50 watt, 200 watt

Answer: 4. 50 watt, 200 watt

R=\(\frac{V^2}{P}=\frac{220 \times 220}{100}=484 \Omega\)

In series, \(\mathrm{R}_{e q} =484+484=968 \Omega\)

∴ \(\mathrm{R}_{e q} =\frac{\mathrm{V}^2}{968}=\frac{220 \times 220}{968}=200 \Omega\)

Question 55. The current (1) in the given circuit is:

1. 1.6 A
2. 2 A
3. 0.32 A
4. 3.2 A

Answer: 2. 2 A

Since, the resistances \(R_{\mathrm{B}}\) and \(R_{\mathrm{C}}\) are connected in series in the given circuit, then their effective resistance will be the same.

⇒ \(R^{\prime} =R_{\mathrm{B}}+R_{\mathrm{C}}\)

=6+6=12 \(\Omega\)

Now, \(R_A\) and \(R^{\prime}\) are in parallel order, hence, the net resistance of the circuit will be,

R=\(\frac{R^{\prime} \times R_{\mathrm{A}}}{R^{\prime}+R_{\mathrm{A}}}=\frac{12 \times 3}{12+3}=\frac{36}{15} \Omega\)

Now, the current flow in the circuit,

i=\(\frac{V}{R}=4.8 \times \frac{15}{36}=2 \mathrm{~A}\)

Question 56. A heating coil is labeled 100 W, 220 V. The coil is cut into two halves and the two pieces are joined in paraded to the same source. The energy now liberated per second is:

1. 25 J
2. 50 J
3. 200 J
4. 400 J

Answer: 4. 400 J

When a heating coil is cut into two halves and then joined in parallel, the coil’s resistance is decreased to one-fourth of its prior value.

As, \(\left(H \alpha \frac{1}{R}\right)\), for constant voltage, the energy liberated per second becomes 4 times, i.e.

4 \(\times 100=400 \mathrm{~J}\)

Question 57. Three resistances each of 4\(\Omega\) are connected to form a triangle. The resistance between any two terminals is:

1. 12 \(\Omega\)
2. \(\frac{2}{1} \Omega\)
3. 6 \(\Omega\)
4. \(\frac{8}{3} \Omega\)

Answer: 4. \(\frac{8}{3} \Omega\)

Here, the two resistances are connected in series and the resultant is connected in parallel with the third resistance.

Therefore, equivalent resistance will be, \(\frac{1}{\mathrm{R}_{\mathrm{BC}}}=\frac{1}{4}+\frac{1}{8}\)

⇒ \(\frac{1}{\mathrm{R}_{\mathrm{BC}}}=\frac{2+1}{8}\)

∴ \(R_{B C}=\frac{8}{3} \Omega\)

Question 58. Six similar bulbs are connected as shown in the figure with a DC source of emf E and zero internal resistance. The ratio of power consumption by the bulbs when (1) all are glowing and (2) in the situation when two from section A and one from section B are glowing will be:

1. 9: 4
2. 1: 2
3. 2: 1
4. 4: 9

Answer: 1. 9: 4

1. When all bulbs are glowing then,

Here, \(R_{e q}=\frac{R}{3}+\frac{R}{3}=\frac{2 R}{3}\)

Power, \(P_i=\frac{E^2}{R_{\text {eq }}}+\frac{3 E^2}{2 R}\)

(2) Two from section A and one from section B are glowing,

Then \(R_{e q}=\frac{R}{2}+R=\frac{3 R}{2}\)

Power, \(P_f=\frac{2 E^2}{3 R}\)

From (1) and (2),

∴ \(\frac{P_i}{P_f}=\frac{3 E^2 3 R}{2 R \cdot 2 E^2}\)=9: 4

Question 59. The internal resistance of 2.1 V cell which gives a current of 0.2 A through a resistance of 10\(\Omega\) is:

1. 0.2\(\Omega\)
2. 0.5\(\Omega\)
3. 0.8\(\Omega\)
4. 1.0\(\Omega\)

Answer: 2. 0.5\(\Omega\)

⇒ \(\mathrm{I} =\frac{E}{r+R}\)

0.2 =\(\frac{2.1}{r+10}\)

r =0.5 \(\Omega\)

Question 60. A cell having an EMF 8 and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by:

Answer: 3.

E=\(I(R+r)=I R+I r\)

and E=\(V+I r \)

E=\(V+\frac{E n}{R+r}\)

V=\(E-\frac{E n}{R+r} \times r\)

Question 61. A student measures the terminal potential difference (V) of a cell of (of emf e and internal resistance r) as a function of the current (l) flowing through it. The slope and intercept of the graph between V and l, then respectively, equal:

1. e and – r
2. – r and e
3. r and – e
4. – e and r

Answer: 2. – r and e

Using ohm’s law, \(\frac{d V}{d \mathrm{I}}\) =-r

and V = E,

if I =0

slope of graph =-r

And Intercept=E

Question 62. For a cell, a terminal potential difference is 2.2 V when the circuit is open. If it reduces to 1.8 V when the cell is connected to a resistance of 5\(\Omega\). The internal resistance of cell (r) is then

1. \(\frac{10}{9} \Omega\)
2. \(\frac{9}{10} \Omega\)
3. \(\frac{11}{9} \Omega\)
4. \(\frac{5}{9} \Omega\)

Answer: 1. \(\frac{10}{9} \Omega\)

The terminal potential difference, V=E-I r

V=\(E-\left[\frac{E}{R-r}\right] r=\frac{E R}{R+r}\)

From given condition =E=2.2 and where R=5

then potential, V=1.8 \(\mathrm{~V}\)

Therefore, 1.8=\(\frac{2.2 \times 5}{5+r}\)

= \(\frac{10}{9} \Omega\)

Question 63. A set of ‘n equal resistors, of value ‘R’ each, are connected in series to a battery of emf ‘E and internal resistance The current drawn is I. Now, the ‘n resistors are connected in parallel to the same battery. Then, the current drawn from the battery becomes 10I. The value of ‘n is :

1. 20
2. 11
3. 10
4. 9

Answer: 3. 10

According to the question,

When n equal resistors of resistance R connected in series then Current, I=\(\frac{E}{n R+r}\) → Equation 1

Where, r= internal resistance of the battery

nr= equivalent resistance of n resistors in series

In question,r=R

I=\(\frac{E}{R(n+1)}\)  → Equation 2

Similarly when n equal resistors of resistance R are connected in parallel then,

Current, \(I^{\prime}=\frac{E}{\frac{R}{n}+R}\)

Where, \(\frac{R}{n}={ }^n\) equivalent resistance of n resistors in parallel

It is given that, \(\Gamma\)=10 I

10 I=\(\frac{E}{\frac{R}{n}+R}=\frac{n E}{(n+1) R}\) Equation 2

From (1) and (2),

10\(\left(\frac{E}{R(n+1)}\right) =\frac{n E}{R(n+1)}\)

n =10

10 I=\(\frac{R}{\frac{R}{n}+R}\)

Divide (2) by (1)

10 =\(\frac{(n+1) R}{\left(\frac{1}{n}+1\right) R}\)

n =10

Question 64. A battery consists of a variable number ‘n of identical cells (having internal resistance V each) which are connected in series. The terminals of the battery are short-circuited and the current I is measured. Which of the graphs shows the correct relationship between I and n?

Answer: 3.

Since, I=\(\frac{n E}{n r}=\frac{E}{r}\)

So, I am independent of n and i is constant.

Question 65. Two cells, having the same e.m.f. are connected in series through an external resistance R. Cells have internal resistances \(r_1\) and \(r_2\left(r_1>r_2\right)\) respectively. When the circuit is closed, the potential difference across the first cell is zero. The value of l is:

1. \(r_1+r_2\)
2. \(r_1-r_2\)
3. \(\frac{r_1+r_2}{2}\)
4. \(\frac{r_1-r_2}{2}\)

Answer: 2. \(r_1-r_2\)

According to the question, \(E-I r_1=0 and \mathrm{I} =\frac{E+E}{r_1+r_2+R} \)

\(\frac{E}{r_1} =\frac{2 E}{r_1+r_2+R} \) \(r_1+r_2+R =2 r_1-r_2\)

R =\(r_1-r_2\)

Question 66. Two batteries, one of EMF 18 volts and internal resistance 2 Ω and the other of EMF 12 volts and internal resistance 1 Ω, are connected as shown. The voltmeter V will record a reading of:

1. 30 volt
2. 18 volt
3. 15 volt
4. 14 volt

Answer: 4. 14 volt

Reading of voltmeter =\(\frac{\frac{E_1}{r_1}+\frac{E_2}{r_2}}{\frac{1}{r_1}+\frac{1}{r_2}}=\frac{E_1 r_2+E_2 r_1}{r_1+r_2}\)

Putting value we get 14 volts.

Question 67. For the circuit shown in the figure, the current I will be: 

1. 0.75 A
2. 1 A
3. 1.5 A
4. 0.5 A

Answer: 2. 1 A

By \(\mathrm{KVL}\) in a closed loop \(\mathrm{ABCDA}\),

⇒ \(V_{\mathrm{A}}-I \times 4-I \times 1+4-I \times 1+2 =V_{\mathrm{A}} \)

⇒ \(-6 \mathrm{I}+6\) =0

I =1 \(\mathrm{~A}\)

Question 68. For the circuit given below, the Kirchhoffs loop rule for the loop BCDEB is given by the equation:

1. \(-\mathrm{i}_2 \mathrm{R}_2+\mathrm{E}_2-\mathrm{E}_3+\mathrm{i}_3 \mathrm{R}_1\)=0
2. \(\mathrm{i}_2 \mathrm{R}_2+\mathrm{E}_2-\mathrm{E}_3-\mathrm{i}_3 \mathrm{R}_1\)=0
3. \(\mathrm{i}_2 \mathrm{R}_2+\mathrm{E}_2-\mathrm{E}_3+\mathrm{i}_3 \mathrm{R}_1\)=0
4. –\(\mathrm{i}_2 \mathrm{R}_2+\mathrm{E}_2+\mathrm{E}_3+\mathrm{i}_3 \mathrm{R}_1\)=0

Answer: 2. \(\mathrm{i}_2 \mathrm{R}_2+\mathrm{E}_2-\mathrm{E}_3-\mathrm{i}_3 \mathrm{R}_1\)=0

The circuit diagram is given by,

Applying the KVL rule to Loop BCDEB.

Question 69. The potential difference \(\left(V_A-V_B\right)\) between the points A and B in the given figure is:

1. – 3 V
2. + 3 V
3. + 6 V
4. + 9 V

Answer: + 9 V

Applying Kirchoff’s law

⇒ \(\mathrm{V}_{\mathrm{B}} =\mathrm{V}_{\mathrm{A}}-(2 \times 2)-3-3(2 \times 1)\)

∴ \(\mathrm{V}_{\mathrm{A}}-\mathrm{V}_{\mathrm{A}} =9 \mathrm{~V}\)

Question 70. In the circuit shown cells A and B have negligible resistances. For V_A =12 V, R₁= 500 Ω, and R = 100 Ω the galvanometer (G) shows no deflection. The value of V_B is:

1. 4 V
2. 2V
3. 12 V
4. 6V

Answer: 2. 2V

The situation is shown in the given figure. then we use Kirchhofl’s law

500 I+100 I =12

I =\(\frac{12 \times 10^{-2}}{6}=2 \times 10^{-2} \mathrm{~A} \)

∴ \(V_B =100\left(2 \times 10^{-2}\right)=2 \mathrm{~V}\)

Question 71. In the circuit shown in the figure, if the potential at point A is taken to be zero, the potential at point B is:

1. – 1 V
2. + 2 V
3. -2 V
4. + 1 V

Answer: 4. + 1 V

Using kirchhoff’s law in loop A C D B

⇒ \(V_A+1+(1)(2)-2 =V_B\)

0+1 =\(V_B\)

∴ \(V_B \)=1 volt

Question 72. Consider the following two statements;

(1) Kirchhoff’s junction law follows from the conservation of charge

(2) Kirchhoff’s loop law follows from the conservation of energy.

Which of the following is correct?

1. Both (1) and (2) are wrong.
2. (1) is correct and (2) is wrong.
3. (1) is wrong and (2) is correct.
4. Both (1) and (2) are correct.

Answer: 4. Both (1) and (2) are correct.

Kirchhoff’s second law follows from the conservation of energy.

Question 73. See the electrical circuit shown in the figure which of the following equations is a correct equation for it?

1. \(e_1-\left(i_1+i_2\right) R-i_1 r_1\)=0
2. \(e_2-i_1 r_2-e_1-i_1 r_1\)=0
3. \(-e_2-\left(i_1+i_2\right) R+i_2 r_2\)=0
4. \(e_1-\left(i_1+i_2\right) R+i_1 r_1\)=0

Answer: 1. \(e_1-\left(i_1+i_2\right) R-i_1 r_1\)=0

Applying Kirchhoff’s law, \(\Sigma \)V=0

Here \(\epsilon_1-\left(i_1+i_2\right) R-i_1 r_1\)=0

Question 74. KirchhofFs first and second laws of electrical circuits are consequences of:

1. conservation of energy and electric charge respectively
2. conservation of energy
3. conservation of electric charge and energy respectively
4. conservation of electric charge

Answer: 3. conservation of electric charge and energy respectively

Kirchhoffs first and second laws of electrical circuits are consequences of the conservation of energy.

Question 75. Kirchhoff’s first law of electricity follows:

1. the only law of conservation of energy
2. the only law of conservation of charge
3. law of conservation of both energy and charge
4. sometimes law of conservation of energy and some other times law of conservation of charge

Answer: 2. only the law of conservation of charge

Kirchhoff’s first law applies to currents at a junction in a circuit. It states that at a junction in an electrical circuit, the sum of currents flowing into the junction is equal to the sum of currents flowing out of the junction. Kirchhoff’s first law is in favor of the law of charge conservation. This is because a point in a circuit cannot be both a source as well as a sink of charge.

Question 76. The resistance of the four. RMS P, Q, R, and S in a Wheatstone’s bridge are 10 Ω. 30 Ω, 30 Ω, and 90 Ω, respectively. The emf and internal resistance of the cell are 7 V and 5 Ω respectively. If the galvanometer resistance is 50Ω, the current drawn from the cell will be:

1. 1.0 A
2. 0.2 A
3. 0.1A
4. 2.0 A

Answer: 2. 0.2 A

Total resistance of Wheatstone Bridge,

=\(\frac{(40)(120)}{40+120}=30 \Omega\)

Current through the coil,

= \(\frac{7 \mathrm{~V}}{(5+30) \Omega}=\frac{1}{5} \mathrm{~A}\)

= 0.2 \(\mathrm{~A}\)

Question 77. Three resistances P, Q, and R each of 2 Ω, and an unknown resistance S form the four arms of a Wheatstone bridge circuit. When a resistance of 6Ω is connected in parallel to S the bridge gets balanced. What is the value of S’?

1. 3 Ω
2. 6 Ω
3. 1 Ω
4. 2 Ω

Answer: 1. 3 Ω

Let X be the equivalent resistance between S and 6 \(\Omega\)

The equivalent circuit is,

Now for the balanced Wheatstone bridge, we have

⇒ \(\frac{R}{X}=\frac{R}{X}=\frac{1}{2}\)

X=2 \(\Omega\)

Now for the balanced Wheatstone bridge, we have

⇒ \(\frac{R}{X}=\frac{R}{X}=\frac{1}{2}\)

X=2 \(\Omega\)

from equation (1) we have

⇒ \(\frac{1}{2}=\frac{1}{S}+\frac{1}{6}\)

⇒ \(\frac{1}{S}=\frac{1}{2}-\frac{1}{6}=\frac{2}{6}\)

S=3 \(\Omega\)

Question 78. In the circuit shown, if a conducting wire is connected between points A and B, the current in this wire will:

1. flow from B to A
2. flow from A to B
3. flow in the direction which will be decided by the value of V
4. be zero.

Answer: 1. flow from B to A

According to the diagram,

⇒ \(V_A-V_B =\left[V-\left(\frac{V}{8} \times 4\right)\right]-\left[V-\left(\frac{V}{4} \times 1\right)\right]\)

=\(-\frac{V}{2}+\frac{V}{4}=-\frac{V}{4}\)

∴ \(V_B >V_A\) .

Question 79. For the network shown in the figure the value of the current i is:

1. \(\frac{9 \mathrm{~V}}{35}\)
2. \(\frac{18 \mathrm{~V}}{5}\)
3. \(\frac{5 \mathrm{~V}}{9}\)
4. \(\frac{5 \mathrm{~V}}{18}\)

Answer: 4. \(\frac{5 \mathrm{~V}}{18}\)

Since the network is balanced, it is Wheatstone’s bridge. Therefore, no current flows through the arm AC,

Here \( R_1\) and \(R_2\) are in series,

⇒ \(R_1{ }^{\prime}=R_1+R_2=4+2=6 \Omega\)

⇒ \(R_3\) and \(R_4\) are in series

⇒ \(R^{\prime \prime}=R_3+R_4=6+3=9 \Omega\)

Now \(R^{\prime} and R^{\prime \prime}\) are in parallel,

⇒ \({1}{R_{e q}} =\frac{1}{R^{\prime}}+\frac{1}{R^{\prime \prime}}\)

= \(\frac{1}{6}+\frac{1}{9}=\frac{5}{18}\)

⇒ \(R_{e q} =\frac{16}{5}\)

Now from V =\(I R_{e q}\)

I = \(\frac{V}{R_{e q}}=\frac{5}{18} \mathrm{~V}\)

Question 80. In a Wheatstone’s bridge, all four arms have equal resistance R. If the resistance of the galvanometer arm is also R, the equivalent resistance of the combination as seen by the battery is:

1. \(\frac{R}{4}\)
2. \(\frac{R}{2}\)
3. R
4. 2 R

Answer: 3. R

Resistance seen by the battery = Equivalent resistance between A and B is R.

Question 81. A Wheatstone bridge is used to determine the value of unknown resistance X by adjusting the variable resistance Y as shown in the figure. For the most precise measurement of X, the resistances P and Q.

1. should be approximately equal to 2X
2. should be approximately equal and small
3. should be very large and unequal
4. do not play any significant role

Answer: 2. should be approximately equal and are small

For a balanced Wheatstone bridge, the current through a galvanometer is zero.\(\frac{P}{Q}=\frac{X}{Y}\)

So, resistance P and Q should be approximately equal and small.

Question 82. A resistance wire connected in the left gap of the meter bridge balances a 10 Ω resistance in the right gap at a point that divides the bridge wire in the ratio 3: 2. If the length of the resistance wire is 1.5 m, then the length of 1Ω of the resistance wire is :

1. 1.0 x 10-1 m
2. 1.5 x 10-1 m
3. 1.5 x 10-2 m
4. 1.0 x 10-2 m

Answer: 1. 1.0 x 10-1 m

The meter bridge is,

Ratio of bridge wire, \(\frac{x_1}{x_2}=\frac{3}{2}\)  → Equation 1

For balance condition of meter bridge, \(\frac{R}{10}=\frac{x_1}{x_2}\) →  Equation 2

From eq. (1) and (2),

⇒ \(\frac{R}{10} =\frac{3}{2}\)

⇒ \(\mathrm{R} =\frac{3}{2} \times 10=15 \Omega\)

So the length of wire whose resistance is 10 \Omega is 1.5 \(\mathrm{~m}\).

Length of 1 \(\Omega\) resistance is,\(\frac{1.5}{15}=0.1=1 \times 10^{-1} \mathrm{~m}\) .

Question 83. The meter bridge is shown in the balance position with \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l_1}{l_2}\). If we now interchange the positions of the galvanometer and cell, will the bridge work? If yes, that will be balanced conduction?

1. \(yes \frac{\mathrm{P}}{\mathrm{Q}}=\frac{l_2-l_1}{l_2+l_1}\)
2. don’t all no null point
3. yes \(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l_2}{l_1}\)
4. yes,\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l_1}{l_2}\)

Answer: 4. yes,\(\frac{\mathrm{P}}{\mathrm{Q}}=\frac{l_1}{l_2}\)

The meter bridge is based on a balanced Wheatstone bridge.

If we interchange the position of the Galvanometer and cell then there is no effect because is in balance Condition, So \(\frac{P}{Q}=\frac{l_1}{l_2}\)

Question 84. The resistance in the two arms of the meter bridge is 5 \(\Omega\) and R \(\Omega\), respectively. When the resistance R is shunted with an equal resistance the new balance point is at 1.6 l₁. The resistance R is:

1. 10 \(\Omega\)
2. 15 \(\Omega\)
3. 20 \(\Omega\)
4. 25 \(\Omega\)

Answer: 2. 15 \(\Omega\)

In the First case,

At balance point,\(\frac{5}{R}=\frac{l_1}{100-l_1}\) →  Equation 1

In the second case,

At balance point,\(\frac{5}{\left(\frac{R}{2}\right)}=\frac{1.6 l_1}{100-1.6 l_1}\)  → Equation 2

Divide eq. (1) by eq (2), We get,

⇒ \(\frac{1}{2} =\frac{100-1.6 l_1}{1.6\left(100-l_1\right)}\)

⇒ \(160-1.6 l_1 =200-3.2 l_1\)

⇒ \(1.6 l_1 =40 or l_1=\frac{40}{1.6}=25 \mathrm{~cm}\)

Substituting this value in eq (1), we get,

⇒ \(\frac{5}{R} =\frac{25}{75}\)

∴ \(\mathrm{R} =\frac{375}{25} \Omega=15 \Omega\) .

Question 85. In a potentiometer circuit, a cell of EMF 1.5 V gives a balance point at 36 cm length of wire. If another cell of EMF 2.5 V replaces the first cell, then at what length of the wire, the balance point occur?

1. 60 cm
2. 21.6 cm
3. 64 cm
4. 62 cm

Answer: 1. 60 cm

Given, \(\varepsilon_1=1.5 \mathrm{~V}\)

Balance length,

We know, \(l_1 =36 \mathrm{~cm}\)

⇒ \(\varepsilon_2 =2.5 \mathrm{~V}\)

⇒ \(l_2 =?\)

⇒ \(\frac{\varepsilon_1}{\varepsilon_2}=\frac{l_1}{l_2}\)

⇒ \(l_2=\frac{\varepsilon_2 l_1}{\varepsilon_1}=\frac{2.5 \times 36}{1.5}\)

⇒ \(l_2=36 \times \frac{5}{3}\)

∴ \(l_2=60 \mathrm{~cm}\)

Question 86. A potentiometer is an accurate and versatile device to make electrical measurements of EMF because the method involves:

1. cells
2. potential gradients
3. a condition of no current flow through the galvanometer
4. a combination of cells, galvanometer, and resistance

Answer: 3. a condition of no current flow through the galvanometer

Reading of potentiometers is accurate because while taking reading it does not draw any current from the circuit.

Question 87. A potentiometer wire is 100 cm long and a constant potential difference is maintained across it. Two cells are connected in series in opposite directions. The balance points are obtained at 50 cm and 10 cm from the positive end of the wire in the two cases. The ratio of emf is:

1. 5: 4
2. 3: 4
3. 3: 2
4. 5: 1

Answer: 3. 3: 2

The emf of the cell is directly proportional to the balancing length, \(E \propto l\)

In the question, two cases are given. In the first case cells are connected in series, \(\varepsilon_1=E_1+E_2\)=50  → Equation 1

In \(II ^{\text {nd }}\) case cells are connected in series but in opposite direction

⇒ \(\varepsilon_2=E_1-E_2\)=10  → Equation 2

From eq. (1) \(\div \)(2)

we get,\(\frac{E_1+E_2}{E_1-E_2} =\frac{50}{10}\)

⇒ \(\frac{E_1}{E_2} =\frac{5+1}{5-1} \)

= \(\frac{6}{4}=\frac{3}{2}\)=3: 2

Question 88. A potentiometer wire has a length of 4 m and resistance of 8 \(\Omega\). The resistance that must be connected in series with the wire and an accumulator of emf 2 V, so as they get a potential gradient of 1 m V per cm on the wire is:

1. 32 \(\Omega\)
2. 40 \(\Omega\)
3. 44 \(\Omega\)
4. 48 \(\Omega\)

Answer: 1. 32 \(\Omega\)

Given resistance of potentiometer, R=8 \(\Omega\) emf of accumulator, E=2 \(\mathrm{~V}\)

Potential gradient, \(\frac{d v}{d r}=1 \mathrm{mV} / \mathrm{cm}\)

Potential due to wire of length, =1 \times 400

= \(400 \mathrm{mV}=0.4 \mathrm{~V}\)

Let a resistor \(R_s\) is connected in series, then

⇒ \(\Delta V =\frac{V}{R+R_5} \times R\)

0.4 =\(\frac{2}{8+R} \times 8\)

8+R =\(\frac{16}{0.4}\)=40

40-8 =32 \(\Omega\)

Question 89. A potentiometer wire of length L and a resistance r are connected in series with a battery of e.m.f. E0 and a resistance r₁. An unknown e.m.f. E is balanced at a length l of the potentiometer wire. The e.m.f E will be given by:

1. \(\frac{L E_0 r}{l r_1}\)
2. \(\frac{E_0 r}{\left(r+r_1\right)} \cdot \frac{l}{L}\)
3. \(\frac{E_0 l}{L}\)
4. \(\frac{L E_0 r}{\left(r+r_1\right) l}\)

Answer: 2. \(\frac{E_0 r}{\left(r+r_1\right)} \cdot \frac{l}{L}\)

Current in potentiometer wire is, I=\(\frac{E_0}{r+r_1}\)

The voltage drop across potentiometer wires,

⇒ \(V_0=\frac{E_0 r}{r+r_1}\)

So, E=\(K I=\frac{V_0 I}{L}\)

E=\(\frac{E_0 r l}{\left(r+r_1\right) L}\)

Question 90. A potentiometer circuit has been set up for finding the internal resistance of a given cell. The main battery, used across the potentiometer wire, has an EMF of 2.0 V and a negligible internal resistance. The potentiometer wire itself is 4 m long. When the resistance R, connected across the given cell, has a value of (1) infinity (2) 9.5 Ω The ‘balancing lengths’, on the potentiometer wire are found to be 3 m and 2.85 m, respectively. The value of the internal resistance of the cell is:

1. 0.25 Ω
2. 0.95Ω
3. 0.5 Ω
4. 0.75 Ω

Answer: 3. 0.5 Ω

According to the question, emf , \(\epsilon=2 \mathrm{~V}\)

and Potentiometer wire length, l=4 \(\mathrm{~m}\)

Potential drop per unit length is :

⇒ \(\phi=\frac{\epsilon}{l}=\frac{2}{4}=0.5 \mathrm{~V} / \mathrm{m}\)

In \(1^{\text {st }} case, \epsilon=\phi l_1\)  → Equation 1

In \(2^{\text {nd }} case, \quad V=\phi l_2\)  → Equation 2

From eq. (1) and (2)

⇒ \(\frac{\epsilon}{V}=\frac{l_1}{l_2}\)

Now for \(2^{\text {nd }}\) case

and \(\epsilon^{\prime} =l(r+R)\)

V =I R

r =\(R\left(\frac{l_1}{l_2}-1\right)=9.5\left(\frac{3}{2.85}-1\right)\)

= \(\frac{0.15}{2.85} \times 9.5 \Omega=0.5 \Omega\)

Question 91. A potentiometer circuit is set up as shown. The potential gradient across the potentiometer wire is k volt/cm, and the ammeter, present in the circuit, reads 1.0 A when the two-way key is switched off. The balance points when the key between the terminals (1) 1 and 2 (2) 1 and 3, is plugged in, are found to be at lengths f cm l2 cm respectively, the magnitude of the resistors R and X, in ohm, are then, equal respectively, to:

1. \(\mathrm{k}\left(\mathrm{l}_2-\mathrm{l}_1\right)\) and \(\mathrm{kl}_2\)
2. \(\mathrm{kl}_2 \)and \(\mathrm{k}\left(\mathrm{l}_2-\mathrm{l}_1\right)\)
3. \(\mathrm{k}\left(\mathrm{l}_2-\mathrm{l}_1\right)\) and \(\mathrm{kl}_1\)
4. \(\mathrm{kl}_1\) and \(\mathrm{kl}_2\)

Answer: 2. \(\mathrm{kl}_2 \)and \(\mathrm{k}\left(\mathrm{l}_2-\mathrm{l}_1\right)\)

Let the balancing length for R be \(l_1\) and balancing length for (R+X) is \(l_2\)

Then, i R=k \(l_1\)

and i(R+X)=\(k l_2\)

It is given that, i=1 \(\mathrm{~A}\)

R=k \(l_1 \)  → Equation 1

R+X=k\( l_2\) →  Equation 2

From (1) and (2)

X=k\(\left(l_2-l_1\right)\)

Question 92. A cell can be balanced against 110 cm and 100 cm of potentiometer wire, respectively with and without being short-circuited through a resistance of 10Ω. Its internal resistance is:

1. 1.0 Ω
2. 0.5 Ω
3. 2.0 Ω
4. zero

Answer: 1. 1.0 Ω

In a potentiometer experiment when we find the internal resistance of a cell. Let E be the emf of the cell and V the potential difference.

Then, \(\frac{E}{V}=\frac{l_1}{l_2}\) [\(l_1\). and \(l_2\) are length of wire]

Since, \(\frac{E}{V}=\frac{R+r}{R}[E=I(R+r) an V=1 R]\)

⇒ \(\frac{R+r}{R} =\frac{l_1}{l_2} 1+\frac{r}{R} =\frac{110}{100}\)

⇒ \(\frac{r}{R}=\frac{10}{100}\)

r=\(\frac{1}{10} \times 10=1 \Omega\)

Question 93. The resistivity of the potentiometer wire is 10^-7 Ω-m and its area of cross-section is 10^-6m². When a current i = 0.1 A flows through the wire, its potential gradient is:

1. 10^-2V/m
2. 10^-4 V/m
3. 0.1^-2 V/m
4. 10^-2V/m

Answer: 1. 10^-2V/m

(A) Potential gradient

= Potential fall per unit length =\(\frac{V}{l}\)

= current \(\times\) resistance per unit length

=i \(\times \frac{R}{l}\) .

but, \(\mathrm{R}=\frac{\rho I}{A}\)

\(\frac{R}{I}=\frac{\rho}{A}\)

Potential gradient =i \(\times \frac{\rho}{A}\)

Given, \(\rho=10^{-7} \Omega-\mathrm{m}, i=0.1 \mathrm{~A} and \mathrm{A}=10^{-6} \mathrm{~m}^2\)

Therefore, potential gradient \(\phi=0.1 \times\left(\frac{10^{-7}}{10^{-6}}\right)=0.1 \times \frac{1}{10}\)

∴ \(\phi=0.01=10^{-2} \frac{\mathrm{V}}{\mathrm{m}}\)

Question 94. A potentiometer measures the potential difference more accurately than a voltmeter, because:

1. it has a wire of high-resistance
2. it has a wire of low resistance
3. it does not draw current from the external circuit
4. it draws a heavy current from the external circuit

Answer: 3. it does not draw current from the external circuit

When we use a potentiometer to measure the emf of a cell, no current is pulled from the external circuit. As a result, the actual value of a cell is found in this condition. In this way, a potentiometer is equivalent to an infinite-resistance ideal voltmeter

Question 95. A potentiometer consists of a wire of length 4 m and resistance 10 \(/omega\). It is connected to a cell of emf 2 V. The potential gradient of the wire is

1. 0.5 V/m
2. 2 V/m
3. 5 V/m
4. 10 V/m

Answer: 1. 0.5 V/m

We have, Potential gradient }=\(\frac{\text { Potential applied }}{\text { Length of wire }}\)

⇒ \(\phi=\frac{V}{I}\)

Given, V=2 \(\mathrm{~V}, l=4 \mathrm{~m}\)

∴ \(\phi=\frac{2}{4}=0.5 \mathrm{~V} / \mathrm{m}\)

• Units and Measurements Multiple Choice Questions
• Motion in a Straight Line Multiple Choice Questions
• Motion in a Plane Multiple Choice Questions
• Laws of Motion Multiple Choice Questions
• Work, Energy and Power Multiple Choice Questions
• System of Particles and Rotational Motion Multiple Choice Questions
• Gravitation Multiple Choice Questions
• Mechanical Properties of Solids Multiple Choice Questions
• Mechanical Properties of Fluids Multiple Choice Questions

• Thermal Properties of Matter Multiple Choice Questions
• Thermodynamics Multiple Choice Questions
• Kinetic Theory Multiple Choice Questions
• Oscillations Multiple Choice Questions
• Waves Multiple Choice Questions
• Electric Charges and Fields Multiple Choice Questions
• Electrostatic Potential and Capacitance Multiple Choice Questions
• Current Electricity Multiple Choice Questions
• Moving Charges and Magnetism Multiple Choice Questions
• Magnetism and Matter Multiple Choice Questions
• Electromagnetic Induction Multiple Choice Questions
• Alternating Current Multiple Choice Questions
• Electromagnetic Waves Multiple Choice Questions
• Ray Optics and Optical Instruments Multiple Choice Questions
• Wave Optics Multiple Choice Questions
• Dual Nature of Radiation and Matter Multiple Choice Questions
• Atoms Multiple Choice Questions
• Nuclei Multiple Choice Questions
• Semiconductor Electronics: Materials, Devices and Simple Circuits Multiple Choice Questions

Electrostatic Potential And Capacitance

Question 1. In a certain region of space with a volume of 0.2 m³, the electric potential is found to be 5 V throughout. The magnitude of the electric field in this region is:

1. 0.5 N/C
2. 1 N/C
3. 5 N/C
4. zero

Answer: 1. 0.5 N/C

Given Volume, V=0.2 \(\mathrm{~m}^3\)

Electric potential =5 \(\mathrm{~V}\) (constant)

Electric field =?

Here Electric field, E=\(-\frac{d v}{d r}\)

Here V=5\(\mathrm{~V}\) and constant

E=\(-\frac{d(5)}{d t}\)

= \(\frac{d(\text { constant })}{d t}\)=0

Question 2. A bullet of mass 2 g is having 2 μc. Through what potential difference must it be accelerated, starting from rest, to acquire a speed of 10 m/s?

1. 5 kV
2. 50 kV
3. 5 V
4. 50 V

Answer: 2. 50 kV

Here we apply, \(\frac{1}{2} m v^2\)=q V

V =\(\frac{1}{2} \times \frac{2 \times 10^{-3} \times 10 \times 10}{2 \times 10^{-6}}\)

=50 kV

Question 3. The variation of electrostatic potential with radial distance r from the centre of a positively charged metallic thin shell of radius R is given by the graph:

Answer: 3.

Since electric potential remains constant inside the metallic spherical shell which is the same as at the surface of a spherical shell. Outside the spherical shell V \(\propto \frac{1}{r}\). So, (b) is the r variation of potential (V) with distance r

Question 4. The electric potential at a point in free space due to charge Q coulomb is Q x 10¹¹ V. The electric field at that point is:

1. 4 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)
2. 12 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{20} \mathrm{~V} / \mathrm{m}\)
3. 4 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)
4. 12 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)

Answer: 1. 4 \(\pi \varepsilon_0 \mathrm{Q} \times 10^{22} \mathrm{~V} / \mathrm{m}\)

Since, V =\(\frac{Q}{4 \pi \varepsilon_0 r}\)

Given, V =\(Q \times 10^{11}\)

r =\(\frac{1}{4 \pi \varepsilon_0 \times 10^{11}}\)

Now \(\mathrm{E} =\frac{V}{r}\)

E = \(Q \times 10^{11} \times 4 \pi \varepsilon_0 \times 10^{11}\)

= 4 \(\pi \varepsilon_0 \times 10^{22} \mathrm{~V} / m\)

Read and Learn More NEET Physics MCQs

Question 5. As per the diagram a point charge + q is placed at the origin O. Work done in taking another point charge – Q from the point A [coordinate (0, a)] to another point B [coordinates (a, 0)] along the straight path AB is:

1. zero
2. \(\left(\frac{q Q}{4 \pi \varepsilon_0} \frac{1}{a^2}\right) \cdot \sqrt{2}\) a
3. \(\left(\frac{-q Q}{4 \pi \varepsilon_0} \frac{1}{a^2}\right) \cdot \sqrt{2}\) a
4. \(\left(\frac{q Q}{4 \pi \varepsilon_0} \frac{1}{a^2}\right) \cdot \frac{a}{\sqrt{2}}\)

Answer: 1. zero

Work done is equal to zero because the potential of A and B are the same \(\frac{1}{4 \pi \epsilon_0} \frac{q}{a}\)

No work is done if a particle does not change its potential energy.

The initial potential energy = final potential energy.

Question 6. A short electric dipole has a dipole moment of 16 x 10^-9 cm. The electric potential due to the dipole at a point at a distance of 0.6 m from the centre of the dipole, situated on a line making an angle of 60° with the dipole axis is:\(\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\)

1. 200 V
2. 400 V
3. zero
4. 50 V

Answer: 1. 200 V

Given the electric dipole moment,

P= \(16 \times 10^{-9} \mathrm{~cm}\)

Distance, r=0.6 \(\mathrm{~m}, Angle \theta=60^{\circ}\)

⇒ \(\cos 60^{\circ}=\frac{1}{2}\)

The Electric potential at a point at a distance k at some angle \(\theta\) from electric dipole is V and

V =\(\frac{P \cos \theta}{4 \pi \varepsilon_0 r^2}\)

= 9 \(\times 10^9 \times \frac{16 \times 10^{-9} \times \frac{1}{2}}{(0.6)^2}\)

= 2 \(\times 10^2=200 \mathrm{~V}\)

Question 7. Two hollow conducting spheres of radii R₁ and R₀ (R₁>>R₂) have equal charges. The potential would be:

1. more on the bigger sphere
2. more on the smaller sphere
3. equal on both the spheres
4. dependent on the material property of the sphere

Answer: 2. more on the smaller sphere

For a hollow sphere, an electric potential is \(\mathrm{V}=\frac{\mathrm{kq}}{\mathrm{R}}\)

For sphere 1, \(V_1=\frac{k q}{R_1}\)

For sphere 1, \(V_2=\frac{k q}{R_2}\)

As \(\mathrm{R}_1 \gg \mathrm{R}_2\),

⇒ \(\mathrm{V}_1 \ll \mathrm{V}_2\).

So, the potential is more on the smaller sphere.

Question 8. Two charged spherical conductors of radius R₁ and R₂ are connected by a wire. Then the ratio of surface charge densities of the spheres \((\sigma_1 / \sigma_2)\) is:

1. \(\frac{R_1}{R_2}\)
2. \(\frac{R_2}{R_1}\)
3. \(\sqrt{\left(\frac{R_1}{R_2}\right)}\)
4. \(\frac{R_1^2}{R_2^2}\)

Answer: 2. \(\frac{R_2}{R_1}\)

Given,Radius =\(R_1 \text { and } R_2 \)

Surface density =\(\sqrt{\sigma_1} \text { and } \sqrt{\sigma_2}\)

⇒ \(\mathrm{~V}_1=\mathrm{V}_2\)

⇒ \(\frac{k q_1}{\mathrm{R}_1}=\frac{k q_2}{\mathrm{R}_2} \)

⇒ \(\frac{q_1}{q_2}=\frac{R_1}{R_2}\)  → Equation 1

Since the spheres are connected by wire. Hence, the charge on them will be equal.

⇒ \(q_1 =q_2\)

⇒ \(q_1 =\sigma_1 \mathrm{~A}_1, q_2=\sigma_2 \mathrm{~A}_2\)

⇒ \(q_1 =\sigma_1 4 \pi \mathrm{R}_1^2\)

⇒ \(q_2 =\sigma_2 4 \pi \mathrm{R}_2^2\)

⇒ \(\frac{\sigma_1}{\sigma_2} =\frac{\frac{q_1}{4 \pi \mathrm{R}_1^2}}{\frac{q_2}{4 \pi \mathrm{R}_2^2}}\)

∴ \(\frac{\sigma_1}{\sigma_2} =\frac{\mathrm{R}_2^2}{\mathrm{R}_1^2} \times \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{\mathrm{R}_2}{\mathrm{R}_1}\)

Question 9. Twenty-seven drops of the same size are charged at 220 V each. They combine to form a bigger drop. The potential for a bigger drop is:

1. 660 V
2. 1320 V
3. 1520 V
4. 1980 V

Answer: 4. 1980 V

Given, the No. of drops = 27

Radius = r

Voltage (F)= 220 V

Its total Radius = R

V=?

Bigger sphere volume \(V_B=\frac{4}{3} \pi \mathrm{R}^3\)

Smaller sphere volume \(V_{\mathrm{s}}=\frac{4}{3} \pi r^3\)

⇒ \(27 \frac{4}{3} \pi r^3 =\frac{4}{3} \pi \mathrm{R}^3 \)

⇒ \(27 r^3 =\mathrm{R}^3\)

⇒ \(\mathrm{R} \) =3 r

Charge \(q_1\) on smaller sphere,

⇒ \(\mathrm{V}_0=\frac{q}{4 \pi \varepsilon_0 r}\)

⇒ \(q_1=\mathrm{V}_0 4 \pi \varepsilon_0 r\)

Charge \(q_2\) on bigger sphere,

⇒ \(q_2 =27 q_1\)

∴ \(\mathrm{V} =\frac{q_2}{4 \pi \varepsilon_0 \mathrm{R}}\)

Question 10. Two metal spheres, one of radius R and the other of radius 2R respectively have the same surface charge density \(\sigma\). They are brought in contact and separated. The new charge densities on them will be:

1. \(\sigma_1=\frac{5}{6} \sigma, \sigma_2=\frac{5}{2} \sigma\)
2. \(\sigma_1=\frac{5}{2} \sigma, \sigma_2=\frac{5}{6} \sigma\)
3. \(\sigma_1=\frac{5}{2} \sigma, \sigma_2=\frac{5}{3} \sigma\)
4. \(\sigma_1=\frac{5}{3} \sigma, \sigma_2=\frac{5}{6} \sigma\)

Answer: 4. \(\sigma_1=\frac{5}{3} \sigma, \sigma_2=\frac{5}{6} \sigma\)

⇒ \(\sigma_1=\frac{5}{3} \sigma, \sigma_2=\frac{5}{6} \sigma\)

We know that surface charge density

⇒ \(\sigma=\frac{q}{A}=\frac{q}{4 \pi R^2}\)

q= \(\sigma .4 \pi R^2\)

Before contact of both the spheres X and Y.

For X, \(q_1 =\sigma .4 \pi R^2 \)

⇒ \(q_2 =4 q_1\)

After Contact, \(q_2=\sigma .4 \pi(2 R)^2\)

Here \(\sigma_1=\frac{q_1^{\prime}}{4 \pi R^2}\) and

⇒ \(\sigma_2=\frac{q_2^{\prime}}{4 \pi R\left(2 R^2\right)}\)

Again we know that, V=\(\frac{k q}{\mathrm{R}}\)

So, \(\frac{k q_1^{\prime}}{\mathrm{R}}=\mathrm{K}\)

So, after contact, we can say, \(q_1^{\prime}+q_2^{\prime}=q_1+q_2=5 q_1 \)

⇒ \(q_1{ }^{\prime}+q_2{ }^{\prime}=5 \times \sigma 4 \pi \mathrm{R}^2\)

3 \(q_1^{\prime}=5 \times 6 \times 4 \pi \mathrm{R}^2 \)

3 \(q_1^{\prime}=5 \times 6 \times 4 \pi \mathrm{R}^2 \)

and \(q_2^{\prime}=2 q_1^{\prime}=\frac{10}{3} \times \sigma 4 \pi \mathrm{R}^2\)

Putting the value of \(q_1{ }^{\prime} and q_2\)

∴ \(\sigma_1=\frac{5}{3} \sigma \text { and } \sigma_2=\frac{5}{6} \sigma\)

Question 11. Four point charges -Q, – q, 2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero, is:

1. Q=-q
2. Q=\(-\frac{1}{q}\)
3. Q=q
4. Q=\(\frac{1}{q}\)

Answer: 1. Q=-q

According to the question when the potential at the centre is zero,

⇒ \(V_1+V_2+V_3+V_4\)=0

⇒ \(\frac{\mathrm{KQ}}{r}-\frac{\mathrm{K} q}{r}+\frac{\mathrm{K}(2 \mathrm{Q})}{r}+\frac{\mathrm{K} 2 q}{r}\) =0

⇒ \(-Q-q+2 q+2 Q \)=0

Q =\(-\mathrm{q}\)

Question 12. Four electric charges + q, + q, – q and – q are placed at the comers of a square of side 2L (see figure). The electric potential at point A mid-way between the two charges + q and q, is:

1. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1+\frac{1}{\sqrt{5}}\right)\)
2. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)
3. zero
4. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}(1+\sqrt{5})\)

Answer: 2. \(\frac{1}{4 \pi \varepsilon_0} \frac{2 q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)

⇒ \(V_A =\frac{k q}{L}+\frac{k q}{L}-\frac{k q}{\sqrt{5} L}-\frac{k q}{\sqrt{5} L}\)

= \(\frac{2 k q}{L}\left(1-\frac{1}{\sqrt{5}}\right)\)

= \(\frac{2 q}{L} \times \frac{1}{4 \pi \varepsilon_0}\left(1-\frac{1}{\sqrt{5}}\right)\)

Question 13. Three charges, each + q, are placed at the comers of an isosceles triangle ABC of sides BC and AC, 2a. D and E are the mid j oint of BC and CA. The work done in taking a charge Q from D to E is:

1. \(\frac{q Q}{8 \pi \varepsilon_0 a}\)
2. \(\frac{q \mathrm{Q}}{4 \pi \varepsilon_0 a}\)
3. zero
4. \(\frac{3 q Q}{4 \pi \varepsilon_0 a}\)

Answer: 3. zero

The situation is shown in the diagram,

From the figure, A C =\(B C(\text { given })\)

⇒ \(V_D =V_E\)=V

W =\(Q\left(V_{\mathrm{E}}-V_{\mathrm{D}}\right)\)

=Q(V-V)

W = 0

Question 14. Three concentric spherical shells have radii a, b and c (a< b <c) and have surface charge densities a, – a and o respectively. If V_A, V_B and V_C denote the potentials of the three shells then for c = a + b, we have:

1. \(V_C=V_A \neq V_B\)
2. \(V_C=V_B \neq V_A\)
3. \(V_C \neq V_B \neq V_A\)
4. \(V_C=V_B=V_A\)

Answer: 1. \(V_C=V_A \neq V_B\)

⇒ \(V_A=\frac{1}{4 \pi \varepsilon_0}\left\{\frac{q_A}{a}+\frac{q_B}{b}+\frac{q_C}{c}\right\}\)

=\(\frac{4 \pi}{4 \pi \varepsilon_0}\left\{\frac{a^2 \sigma}{a}-\frac{b^2 \sigma}{b}+\frac{c^2 \sigma}{c}\right\}\)

⇒ \(V_A =\frac{1}{\varepsilon_0}\left\{\frac{a^2 \sigma}{a}-\frac{b^2 \sigma}{b}+\frac{c^2 \sigma}{c}\right\}\)

⇒ \(V_B =\frac{1}{\varepsilon_0}\left\{\frac{a^2 \sigma}{b}-\frac{b^2 \sigma}{b}+\frac{c^2 \sigma}{c}\right\}\)

⇒ \(V_C =\frac{1}{\varepsilon_0}\left\{\frac{a^2 \sigma}{c}-\frac{b^2 \sigma}{c}+\frac{c^2 \sigma}{c}\right\}\)

Using c=a+b, \(V_A=\frac{2 a \sigma}{\varepsilon_0} \)

⇒ \(V_B =\frac{\sigma}{\varepsilon_0}\left(\frac{a^2}{b}+a\right)=\frac{\sigma}{\varepsilon_0} \frac{a c}{b}\)

⇒ \(V_C \frac{\sigma}{\varepsilon_0}\left[\frac{(a+b)(a-b)}{c}+c\right]\)

= \(\frac{\sigma}{\varepsilon_0}(a-b+c)=\frac{2 a \sigma}{\varepsilon_0} \)

⇒ \(V_B =\frac{1}{4 \pi \varepsilon_0} \frac{\sigma 4 \pi c^2}{b}-\frac{1}{4 \pi \varepsilon_0} \frac{\sigma 4 \pi c^2}{b}\)

= \(\frac{\sigma}{\varepsilon_0}\left(\frac{a^2}{b}-b+c\right)\)

Similarly, \(V_C =\frac{\sigma}{\varepsilon_0}(2 a)\)

∴ \(V_A =V_C \neq V_B\)

Question 15. Two concentric spheres of radii R and r have similar charges with equal surface charge densities (o). What is the electric potential at their common centre?

1. \(\frac{\sigma}{\varepsilon_0}\)
2. \(\frac{\sigma}{\varepsilon_0}(R-r)\)
3. \(\frac{\sigma}{\varepsilon_0}(R+r)\)
4. None of these

Answer: 3. \(\frac{\sigma}{\varepsilon_0}(R+r)\)

Let the charges on the spheres be Q and q respectively. The potential at the common center,

V =\(\frac{1}{4 \pi \varepsilon_0}\left(\frac{Q}{R}\right)+\frac{1}{4 \pi \varepsilon_0}\left(\frac{q}{r}\right)\)

= \(\frac{1}{\varepsilon_0}\left[\frac{Q}{4 \pi R^2} \times R+\frac{q}{4 \pi r^2} \times r\right]\)

But, \(\frac{Q}{4 \pi R^2} =\frac{q}{4 \pi R^2}=\sigma\)

⇒ \(\mathrm{V} =\frac{1}{\varepsilon_0}[\sigma R+\sigma r]\)

=\(\frac{\sigma}{\varepsilon_0}(R+r)\)

Question 16. The angle between the electric lines of force and the equipotential surface is:

1. 0°
2. 45°
3. 90°
4. 180°

Answer: 3. 90°

The angle between the electric lines of force and the equipotential surface is 90°.

Question 17. The diagrams below show regions of equipotentials: A positive charge is moved from A to B in each diagram.

1. Maximum work is required to move q in Figure (3).
2. In all four cases, the work done is the same.
3. Minimum work is required to move q in Figure (1).
4. Maximum work is required to move q in Figure (2).

Answer: 2. In all the four cases, the work done is the same.

Work done, W = q \(\Delta V\)

∴ \(\Delta V\) is the same in all the cases so the work done is the same in all the cases.

Question 18. If potential (in volts) in a region is expressed as V(x, y, z) = 6xy -y + 2yz. the electric field in (N/C) at point (1,1, 0) is:

1. \(-(3 \hat{i}+5 \hat{j}+3 \hat{k})\)
2. \(-(6 \hat{i}+5 \hat{j}+2 \hat{k})\)
3. \(-(2 \hat{i}+3 \hat{j}+\hat{k})\)
4. \(-(6 \hat{i}+9 \hat{j}+\hat{k})\)

Answer: 2. \(-(6 \hat{i}+5 \hat{j}+2 \hat{k})\)

From the question, Potential in a region,

⇒ \(V_{(x, y, z)}=6 x y-y+2 y z\)

Electric field, E= \(-\frac{\partial V}{\partial x} \hat{i}-\frac{\partial V}{\partial y} \hat{j}-\frac{\partial V}{\partial z} \hat{k}\)

= \(-6 y \hat{i}-(6 x-1) \hat{j}-2 y \hat{k}\)

⇒ \(E_{(1,1,0)} =(6 \times 1) \hat{i}-(6 \times 1-1) \hat{j}-2 \times 1 \hat{k}\)

= \(-(6 \hat{i}+5 \hat{j}+2 \hat{k}) \mathrm{N} / \mathrm{C}\)

Question 19. In a region the potential is represented by V(x, y, z) = 6x – xy – 8y + 6yz, where V is in volts and x, y, z are in metres. The electric force experienced by a charge of 2 coulomb situated at point (1, 1,1) is:

1. \(6 \sqrt{5} \mathrm{~N}\)
2. 30 \(\mathrm{~N}\)
3. 24 \(\mathrm{~N}\)
4. 4 \(\sqrt{35} \mathrm{~N}\)

Answer: 4. 4 \(\sqrt{35} \mathrm{~N}\)

It is given,

V=6 x-8 x y-8 y+6 y z

We know that, E =\(\frac{\mathrm{d} V}{\mathrm{~d} x}\)  → Equation 1

⇒ \(E_X =\frac{\mathrm{d} V}{\mathrm{~d} x}=6-8 y \)

⇒ \(E_Y =\frac{\mathrm{d} V}{\mathrm{~d} y}=-8 x-8+6 \mathrm{z}\) →  Equation 2

⇒ \(E_{\mathrm{z}} =\frac{d V}{d z}\)=6 y

The values of \(E_X, E_Y\) and \(E_Z\) at (1,1,1) are,

⇒ \(E_X =6-8 \times 1\)=-2

⇒ \(E_Y =-8 \times 1-8+6 \times 1\)=-10

⇒ \(E_Z =6 \times 1\)=6

⇒ \(E_{\text {net }} =\sqrt{(2)^2+(10)^2+(6)^2}\)

=\(\sqrt{4+100+36}=\sqrt{140} \)

=\(\sqrt{35 \times 4}=2 \sqrt{35} \mathrm{~N} / \mathrm{C}\)

F =\(q \cdot E_{n e t}\)

=\(2 \times(2 \sqrt{35})=4 \sqrt{35} \mathrm{~N}\)

Question 20. The electric potential V at any points (x, y, z), all in metres in spaces is given V = 4×2 volt. The electric field at the point (1, 0, 2) in volt/metre is:

1. 8 along the positive X-axis
2. 16 along the negative X-axis
3. 16 along the positive X-axis
4. 8 along the negative X-axis

Answer: 4. 8 along the negative X-axis

It is given that, V=4 x^2

Then We have,E =\(-\left[\hat{i} \frac{\partial V}{\partial x}+\hat{j} \frac{\partial V}{\partial y}+\hat{k} \frac{\partial V}{\partial z}\right]\)

= \(\hat{i} \frac{\partial V}{\partial x}=-\hat{i} \frac{\partial V}{\partial x}\left(4 x^2\right)\)

= \(-8 x \mathrm{Vm}^{-2}\)

∴ \(\mathrm{E}_{(1,0,2)} =-8 \times 1=-8 \hat{i} \cdot \mathrm{Vm}^{-1}\)

Question 21. The electric potential at a point (x, y, z) is given by, \(V=-x^2 y-x z^3+4\). The electric field \(\vec{E}\) at that point is:

1. \(\vec{E}=\left(2 x y+z^3\right) \hat{i}+x^2 \hat{j}+3 x z^2 \hat{k}\)
2. \(\vec{E}=2 x y \hat{i}+\left(x^2+y^2\right) \hat{j}+\left(3 x z-y^2\right) \hat{k}\)
3. \(\vec{E}=z^3 \hat{i}+x y z \hat{j}+z^2 \hat{k}\)
4. \(\vec{E}=\left(2 x y-z^3\right) \hat{i}+x y^2 \hat{j}+3 z^2 x \hat{k}\)

Answer: 1. \(\vec{E}=\left(2 x y+z^3\right) \hat{i}+x^2 \hat{j}+3 x z^2 \hat{k}\)

We know that, E =\(-\frac{d V}{d r}=\left[-\frac{\partial v}{\partial x} \hat{i}-\frac{\partial v}{\partial y} \hat{j}-\frac{\partial v}{\partial z} \hat{k}\right]\)

= \(\left[\hat{i}\left(2 x y+z^3\right)+\hat{j} x^2+\hat{k} 3 x z^2\right]\)

Question 22. Charges +q and -q are placed at points A and B respectively which are a distance 2L apart, C is the midpoint between A and B. The work done in moving a charge +Q along the semicircle CRD is:

1. \(\frac{q Q}{2 \pi \varepsilon_0 L}\)
2. \(\frac{q Q}{6 \pi \varepsilon_0 L}\)
3. \(\frac{q Q}{3 \pi \varepsilon_0 L}\)
4. \(\frac{q Q}{4 \pi \varepsilon_0 L}\)

Answer: 2. \(\frac{q Q}{6 \pi \varepsilon_0 L}\)

W=\(\Delta U=\mathrm{Q}\left(V_D-V_C\right)\)

where, \(V_C\)=0

W =\(Q\left[\frac{q}{4 \pi \varepsilon_0(3 L)}-\frac{q}{4 \pi \varepsilon_0(L)}\right]\)

= \(-\frac{Q q}{6 \pi \varepsilon_0 L}\)

The potential at C is zero because the charges are equal and opposite and the distances are the same. Potential at D due to – q is greater than that at A (+q) because D is closer to B.

∴ It is negative.

Question 23. Two charges q₁ and q₂ are placed 30 cm apart, as shown in the figure. A third charge q₃ is moved along the arc of a circle of radius 40 cm from C to D. The change in the potential energy of the system is \(\frac{V_3}{4 \pi \varepsilon_0} k\)

1. \(8 q_1\)
2. \(6 q_1\)
3. \(8 q_2\)
4. \(6 q_2\)

Answer: 3. \(8 q_2\)

⇒ \(V_i=\frac{1}{4 \pi \epsilon_0}\left[\frac{q_1 q_3}{(0.4)}+\frac{q_1 q_2}{(0.3)}+\frac{q_2 q_3}{(0.5)}\right] \)

\(V_f=\frac{1}{4 \pi \epsilon_0}\left[\frac{q_1 q_3}{(0.4)}+\frac{q_1 q_2}{(0.3)}+\frac{q_2 q_3}{(0.1)}\right]\)

⇒ \(\Delta V =V_f-V_{\mathrm{i}}\)

= \(\frac{1}{4 \pi \epsilon_0} q_2 q_3\left(\frac{1}{0.1}-\frac{1}{0.5}\right)\)

= \(\frac{q_2 q_3}{4 \pi \epsilon_0}\left(10^{-2}\right)\)

= \(\frac{q_3}{4 \pi \epsilon_0}\left(8 q_2\right)\)

k =\(8 q_2\)

Question 24. Identical charges (- q) are placed at each comer of a cube of side ‘b’ then the electrical potential energy of charge (+ q) which is placed at the centre of the cube will be:

1. \(\frac{-4 \sqrt{2} q^2}{\pi \varepsilon_0 b}\)
2. \(\frac{-8 \sqrt{2} q^2}{\pi \varepsilon_0 b}\)
3. \(\frac{-4 q^2}{\sqrt{3} \pi \varepsilon_0 b}\)
4. \(\frac{8 \sqrt{2} q^2}{4 \pi \varepsilon_0 b}\)

Answer: 3. \(\frac{-4 q^2}{\sqrt{3} \pi \varepsilon_0 b}\)

The distance between the charge -q and +q is,

r= \(\sqrt{\frac{(\sqrt{2} b)^2+(b)^2}{2}}=\frac{\sqrt{3}}{2} b\)

The electric potential energy of charge +q is,

V = 8 \(\times \frac{1}{4 \pi \varepsilon_0} \frac{q(-q)}{r}\)

= 8 \(\times \frac{1}{4 \pi \varepsilon_0} \frac{q(-q)}{\frac{\sqrt{3}}{2} b}\)

U =\(\frac{-4 q^2}{\sqrt{3} \pi \varepsilon_0 b}\)

Question 25. In bringing an electron towards another electron, the electrostatic potential energy of the system:

1. decreases
2. increases
3. remains same
4. becomes zero

Answer: 2. increases

The electron is charged negatively. When an electron passes another electron, the same negative charges produce a repulsive force between them. As a result, work is done against this repulsive force to bring them closer together. Electrostatic potential energy is used to store the work.

As a result, the system’s electrostatic potential energy increases. Since the electrostatic potential energy of a system of two electrons, \(\mathrm{U}=\frac{1}{4 \pi \varepsilon_0} \frac{(-e)(-e)}{r}=\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{r}\)

R decreases, and potential energy U increases.

Question 26. A dipole is placed in an electric field as shown. In which direction will it move?

1. Towards the left, its potential energy will increase.
2. Towards the right, its potential energy will decrease.
3. Towards the left, its potential energy will decrease.
4. Towards the right, its potential energy will increase.

Answer: 3. Towards the left its potential energy will decrease.

Since the electric field is growing against the dipole direction hence the dipole will move towards the left due to a decrease in its potential energy.

Question 27. An electric dipole of dipole moment p is aligned parallel to a uniform electric field E. The energy required to rotate the dipole by 90° is:

1. \(p^2 E\)
2. pE
3. infinity
4. \(p E^3\)

Answer: 2. pE

The potential energy of the dipole

U = \(-p E\left(\cos \theta_2-\cos \theta_1\right)\)

⇒ \(\theta_2 =0^{\circ}\)

=\(-p E\left(\cos 90^{\circ}-\cos 0^{\circ}\right)\)

U = PE

Question 28. An electric dipole of dipole moment \(\vec{p}\) is lying along a uniform electric field \(\vec{E}\). The work done in rotating the dipole by:

1. pE
2. \(\sqrt{2} p E\)
3. pE / 2
4. 2PE

Answer: 1. pE

Work done, W =\(\int_0^\theta P E \sin \theta d \theta \)

= P E\((1-\cos \theta)\)

Since, \(\theta=90^{\circ}\)

W =\(P E\left(1-\cos 90^{\circ}\right)\)

Q = PE

Question 29. An electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field the force on it and its potential energy are respectively:

1. 2 q.E and minimum
2. q.E and p.E
3. zero and minimum
4. q.E and maximum

Answer: 3. Zero and minimum

Force on each charge, of dipole

⇒ \(\tilde{F}\)=p E

Total force = zero, they are in the opposite direction

⇒ \(\vec{P}\) and \(\vec{E}\) are parallel to each other

U=\(-\vec{P} \cdot \vec{E}\) is minimum.

Question 30. Some charge is being given to a conductor. Then, its potential:

1. Is maximum at the surface
2. Is maximum at the centre
3. Is the same throughout the conductor
4. Is maximum somewhere between the surface and the

Answer: 3. Is the same throughout the conductor

We know that inside the conductor F = 0.

So, the potential remains the same.

Question 31. The electrostatic force between the metal plates of an isolated parallel plate capacitance C having Q and area A is:

1. proportional to the square root of the distance between the plates.
2. linearly proportional to the distance between the plates.
3. independent of the distance between the plates.
4. inversely proportional to the distance between the plates.

Answer: 3. independent of the distance between the plates.

We know that, For isolated capacitors, Q= constant

⇒ \(F_{\text {plate }}=\frac{Q^2}{2 A \varepsilon_0}\)

So, \(\mathrm{F}\) is independent of the distance between plates.

Question 32. A parallel plate air capacitor has capacity C, distance of separation between plates is d and potential difference V is applied between the plates. The force of attraction between the plates of the parallel plate air capacitor is:

1. \(\frac{C^2 V^2}{2 d}\)
2. \(\frac{C V^2}{2 d}\)
3. \(\frac{C V^2}{d}\)
4. \(\frac{C^2 V^2}{2 d^2}\)

Answer: 2. \(\frac{C V^2}{2 d}\)

According to question,F =\(\frac{Q^2}{2 \varepsilon_0 A} \)

Q =\(C V \text { and } C=\frac{\varepsilon_0 A}{d}\)

⇒ \(\varepsilon_0 A =c d\)

F =\(\frac{C^2 V^2}{2 C d}=\frac{C V^2}{2 d}\)

Question 33. A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an insulating handle. As a result the potential difference between the plates:

1. Increases
2. decreases
3. does not change
4. becomes zero

Answer: 1. Increases

According to the question

⇒ \(\phi\)= Const and a decrease in C means an increase in V.

C =\(\frac{\varepsilon_0 A}{d}\)

Capacitance =\(\frac{\text { Charge }}{\text { Potential difference }}\)

Potential difference =\(\frac{\text { Charge }}{\text { Capacitance }}\) .

Question 34. A parallel plate capacitor having cross-sectional area A and separation d has air in between the plates. Now an insulating slab of the same area but thickness d/2 is inserted between the plates as shown in the figure having a dielectric constant (K = 4). The ratio of the new capacitance to its original capacitance will be:

1. 2: 1
2. 8: 5
3. 6: 5
4. 4: 1

Answer: 2. 8: 5

The capacitance of parallel plate capacitor when the medium is air,

⇒ \(C_{\mathrm{o}}=\frac{\varepsilon_0 A}{d}\)

From \(2^{\text {nd }}\) condition,

⇒ \(A^{\prime}=A \cdot t=\frac{d}{2},\) k=4

v \(\mathrm{C}=\frac{\varepsilon_0 A}{(d-t)+\frac{t}{k}}=\frac{\varepsilon_0 \mathrm{~A}}{\left(d-\frac{d}{2}\right)+\frac{d / 2}{4}}\)

= \(\frac{\varepsilon_0 \mathrm{~A}}{\frac{d}{2}+\frac{d}{8}}=\frac{8}{5} \cdot \frac{\varepsilon_0 \mathrm{~A}}{d}\)

⇒ \(\frac{C}{C_0}=\frac{\frac{8}{5} \frac{\varepsilon_0 A}{d}}{\frac{\varepsilon_0 A}{d}}\)

∴ \(\frac{C}{C_0}=\frac{8}{5}\)

Question 35. The capacitance of a parallel plate capacitor with air as a medium is 6 pF. With the introduction of a dielectric medium, the capacitance becomes 30 pF. The permittivity of the medium is: \(\left(\varepsilon_0=8.85 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\right)\)

1. \(177 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)
2. \(0.44 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)
3. \(5.00 \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)
4. \(0.44 \times 10^{-13} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

Answer: 2. \(0.44 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}\)

Given, \(C_{\mathrm{O}}=6 \mu F\)

⇒ \(C_M=30 \mu \mathrm{F}\)

Dielectric, K=\(\frac{C_M}{C_{\mathrm{O}}}=\frac{30}{6}\)=5

Dermittivity of medium, \(\varepsilon_m =K \times \varepsilon_0=5 \times \varepsilon_0\)

= 5 \(\times 8.854 \times 10^{-12}\)

= \(0.44 \times 10^{-12} \mathrm{C}^2 \mathrm{~N} \mathrm{~m}^{-2}\)

Question 36. Two thin dielectric slabs with dielectric constants K₁ and K₂(K₁ < K₂) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by:

Answer: 2.

Given, the electric field inside the dielectrics will be less than the electric field outside the dielectrics. The electric field inside the dielectric could not be zero. Option (b) is the correct answer.

Question 37. Two parallel metal plates having charge + Q and – Q face each other at a certain distance between them. If the plates are now dipped in the kerosene oil tank, the electric field between the plates will:

1. becomes zero
2. increase
3. decrease
4. remain same

Answer: 3. decrease

Electric field in volume, \(E_0=\frac{\sigma}{2 \varepsilon_0}\)

When plates are dipped in a kerosene oil electric field,

Here,E=\(\frac{\sigma}{2 \epsilon_0 \mathrm{~A}}\)

⇒ \(K<E_0\)

So the electric field between the plates will decrease.

Question 38. A parallel plate condenser with oil (dielectric constant 2) between the plates has capacitance C. If oil is removed, the capacitance of the capacitor becomes:

1. \(\sqrt{2 C}\)
2. 2C
3. \(\frac{C}{\sqrt{2}}\)
4. \(\frac{C}{2}\)

Answer: 4. \(\frac{C}{2}\)

We have, the capacitance of a parallel plate capacitor with dielectric (oil) between its plates is

⇒ \(\mathrm{C}=\frac{K \varepsilon_0 A}{d}\) →  Equation 1

where, \(\varepsilon_0\)= electric permittivity of free space

K= dielectric constant of oil

A = Area of each plate of capacitor

d= distance between two plates

When the dielectric (oil) is removed, then, the capacitor’s capacitance will be,

⇒ \(\mathrm{C}_0=\frac{C}{K}=\frac{C}{2}\)  → Equation 2

On comparing Eqs. (1) and (2), we get

⇒ \(C=K C_0 \)

∴ \(C_0=K C_0\)

Question 39. The equivalent capacitance of the combination shown in the figure is:

1. 3C
2. 2C
3. \(\frac{C}{2}\)
4. \(\frac{3 C}{2}\)

Answer: 2. 2C

Since the capacitor (3) is shorted out by the parallel wire hence the net capacitance is in parallel.

∴ \(C_{\mathrm{P}}=C+C=2 C\)

Question 40. A parallel-plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constants \(k_1, k_2, k_3, k_4\) as shown in the figure below. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by:

1. \(k=k_1+k_2+k_3+3 k_4\)
2. k=\(\frac{2}{k}\left(k_1+k_2+k_3\right)+2 k_4\)
3. \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)
4. \(\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}+\frac{1}{k_3}=\frac{3}{2 k_4}\)

Answer: 3. \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)

Here the capacitance, C=\(\frac{A k \varepsilon_0}{d}\)

The above three capacitors \(C_1, C_2, C_3\) are in parallel and then it is in series with \(C_4\).

Here, \(C_1=\frac{\left(\frac{A}{3}\right) k_1 \varepsilon_0}{\frac{d}{2}}=\frac{2 k_1}{3 k} C\)

⇒ \(C_2=\frac{\left(\frac{A}{3}\right) k_2 \varepsilon_0}{\frac{d}{2}}=\frac{2 k_2}{3 k} C\)

⇒ \(C_3=\frac{\left(\frac{A}{3}\right) k_3 \varepsilon_0}{\frac{d}{2}}=\frac{2 k_3}{3 k} C \)

⇒ \(C_4=\frac{\left(\frac{A}{3}\right) k_4 \varepsilon_0}{d}=\frac{2 k_4}{k} C\)

Now, the equivalent capacitance for the combination of four capacitors is

or \(\frac{1}{C_{e q}}=\frac{1}{C_1+C_2+C_3}+\frac{1}{C_4}\)

or \(\frac{1}{C}=\frac{3 k}{2 C}\left[\frac{1}{k_1+k_2+k_3}\right]+\frac{k}{2 k_4 C} (as C_{\text {eq }}=\mathrm{C} ) \)

or \(\frac{2}{k}=\frac{3}{k_1+k_2+k_3}+\frac{1}{k_4}\)

Question 41. Three capacitors each of capacitance C and of break-down voltage V are joined in series. The capacitance and breakdown voltage of the combination will be:

1. \(\frac{C}{3}, \frac{V}{3}\)
2. 3 C, \(\frac{V}{3}\)
3. \(\frac{C}{3}\), 3 V
4. 3 C, 3 V

Answer: 3. \(\frac{C}{3}\), 3 V

Here V=3 x

⇒ \(C_{e q}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}\)

∴ \(C_{e q}=\frac{C}{3}\)

Question 42. A network of four capacitors capacity equal C₁ = C, C2= 2C, C₃ = 3C and C₄= 4C are conducted to a battery as shown in the figure. The ratio of the change on C₂ and C₄.

1. \(\frac{4}{7}\)
2. \(\frac{3}{22}\)
3. \(\frac{7}{4}\)
4. \(\frac{22}{3}\)

Answer: 2. \(\frac{3}{22}\)

Here, \(C_1, C_2, C_3\) are in series.

⇒ \(\frac{1}{C^{\prime}}=\frac{1}{C}+\frac{1}{2 C}+\frac{1}{3 C}\)

⇒ \(\frac{1}{C^{\prime}}=\frac{6+3+2}{6 C}=\frac{11}{6 C}\)

⇒ \(C^{\prime \prime}=\frac{6 C}{11}\)

All the capacitors in branch number 1 are in series so the charge on each number capacitor is:

⇒ \(Q^{\prime}=\frac{6}{11} C V\)

Also charge on capacitor \(C_4 is Q=4 \mathrm{~V}\)

Ratio =\(\frac{Q^{\prime}}{Q}=\frac{6 C V}{11 \times 4 C V} \)

= \(\frac{3}{22}\)

Question 43. Three capacitors each of capacity 4 \(\mu\)F are to be connected in such a way that the effective capacitance is 6 \(\mu\)F. This can be done by:

1. connecting all of them in a series
2. connecting them in parallel
3. connecting two in series and one in parallel
4. connecting two in parallel and one in series

Answer: 3. connecting two in series and one in parallel

⇒ \(\mathrm{C}_{\mathrm{AB}} =(2+4) \mu \mathrm{F}\)

=6 \(\mu \mathrm{F}\)

Question 44. A capacitor of capacitance C₁ charged up to V volt and then connected to an uncharged capacitor C₂. Then, the final potential difference across each capacitor will be:

1. \(\frac{C_2 V}{C_1+C_2}\)
2. \(\frac{C_1 V}{C_1+C_2}\)
3. \(\left(1+\frac{C_2}{C_1}\right) V\)
4. \(\left(1-\frac{C_2}{C_1}\right) V\)

Answer: 2. \(\frac{C_1 V}{C_1+C_2}\)

_⇒ \(V^{\prime}=\frac{C_1 V_1+C_2 V_2}{C_1+C_2}\left( V_2=0\right)\)

∴ \(V^{\prime}=\frac{C_1 V_1}{C_1+C_2}\)

Question 45. A capacitor of capacitance C = 900 pF is charged fully by 100V battery B as shown in figure (1). Then it is disconnected from the battery and connected to another uncharged capacitor of capacitance C = 900 pF as shown in Fig (b). The electrostatic energy stored by the system (2) is:

1. \(4.5 \times 10^{-6} \mathrm{~J}\)
2. 3.25 \(\times 10^{-6} \mathrm{~J}\)
3. 2.25 \(\times 10^{-6} \mathrm{~J}\)
4. 1.5 \(\times 10^{-6} \mathrm{~J}\)

Answer: 3. 2.25 \(\times 10^{-6} \mathrm{~J}\)

Given: \(\mathrm{C}_1=\mathrm{C}_2=900 \mathrm{pF}\)

⇒ \(\mathrm{V}_1=100 \mathrm{~V}, \mathrm{~V}_2=0 \mathrm{~V}\)

When \(\mathrm{C}_1 and \mathrm{C}_2\) are joined,

V =\(\frac{C_1 V_1+C_2 V_2}{C_1+C_2}\)

= \(\frac{900 \times 100+0}{1800}=50 \mathrm{~V}\)

Energy, U =\(\frac{1}{2}\left(C_1+C_2\right) V^2 \)

= \(\frac{1}{2} \times 1800 \times 10^{-12} \times 50 \times 50\)

= 2.25 \(\times 10^{-6} \mathrm{~J}\)

Question 46. A parallel plate capacitor has a uniform electric field ‘ E ’ in the space between the plates. If the distance between the plates is ‘d’ and the area of each plate is ‘A’, the energy stored in the capacitor is: (\(\varepsilon_0\) = permittivity of free space)

1. \(\frac{1}{2} \varepsilon_0 E^2\)
2. \(\varepsilon_0 E A d\)
3. \(\frac{1}{2} \varepsilon_0 E^2 A d\)
4. \(\frac{E^2 A d}{\mathrm{e}_0}\)

Answer: 3. \(\frac{1}{2} \varepsilon_0 E^2 A d\)

Given, Electric Field =E

Distance between plates =d

Area of plates =A

Energy =?

We know, \(\frac{\text { Energy }}{\text { Vol }}=\frac{1}{2} \varepsilon_0 E^2\)

Energy =\(\frac{1}{2} \varepsilon_0 E^2 \times \mathrm{Vol} \)

Energy =\(\frac{1}{2} \varepsilon_0 E^2 \mathrm{Ad}\)

Question 47. Two identical capacitors C₁ and C₂ of equal capacitance are connected as shown in the circuit. Terminals a and b of the key k are connected to charge capacitor C₁ using a battery of emf V volt. Now, disconnecting a and b the terminals b and c are connected. Due to this, what will be the percentage loss of energy?

1. 75%
2. 0%
3. 50%
4. 25%

Answer: 3. 50%

We know from the question,

On switching key at point C, \(\frac{90-q}{\mathrm{C}} =\frac{q}{\mathrm{C}}\)

2 q =90

q =\(\left(\frac{90}{2}\right)\)

⇒ \(V_f =\frac{1}{2}\left(\frac{90}{2}\right)^2 \times \frac{1}{C}+\frac{1}{2} \times\left(\frac{90}{2}\right)^2 \times \frac{1}{C}\)

⇒ \(V_f =\frac{90^2}{4 \mathrm{C}}\)

⇒ \(V_f =\frac{1}{4} C V^2\)

⇒ \(\text { Loss }^2 =\frac{V_i-V_f}{V_i} \times 100\)

= \(\frac{\left(\frac{1}{2}-\frac{1}{4}\right) C V^2}{\frac{1}{2} C V^2} \times 100=50 \%\)

Question 48. A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of the resulting system:

1. increases by a factor of 4
2. decreases by a factor of 2
3. remains the same
4. increases by a factor of 2

Answer: 2. decreases by a factor of 2

Change An Capacitor, q = CV

When it is connected to another uncharged capacity,

⇒ \(V_C=\frac{q_1+q_2}{C_1+C_2}=\frac{q+0}{C+C}=\frac{V}{2}\)

Initial energy, \(U_i=\frac{1}{2} C V^2\)

Final energy, \(U_f=\frac{1}{2} C\left(\frac{V}{2}\right)^2\)

= \(\frac{1}{2} C\left(\frac{V}{2}\right)^2=\frac{C V^2}{4}\)

Loss of energy, \(U_i-V_f=\frac{C V^2}{4}\)

∴ i.e. decreases by a factor of 2.

Question 49. A capacitor of 2 μF is charged as shown in the figure. When the switch S is turned to position 2, the percentage of its stored energy dissipated is:

1. 20%
2. 75%
3. 80%
4. 0%

Answer: 3. 80%

First when switch S is connected to point 1. Then,

Initial energy stored in capacitor 2 \(\mu \mathrm{F}\) is,

⇒ \(U_i=\frac{1}{2}(2 \mu \mathrm{F}) V^2\left[Q E=\frac{1}{2} C V^2\right]\)

Second when switch S is connected to point 2, then

⇒ \(U_i=\frac{C_1 V_1}{C_1+C_2}=\frac{2 V}{10}=0.2 \mathrm{~V}\)

Final energy in both the capacitors,

⇒ \(\mathrm{U}_f =\frac{1}{2}\left(C_1+C_2\right) V_i^2 \)

=\(\frac{1}{2} \times 10\left(\frac{2 \mathrm{~V}}{10}\right)^2=0.2 \mathrm{~V}^2\)

So, energy dissipated = \(\frac{V^2-0.2 V^2}{V^2} \times 100=80 \%\)

Question 50. A parallel plate air capacitor of capacitance C is connected to a cell of emf V and then disconnected from it. A dielectric slab of electric constant K, which can just fill the air gap of the capacitor, is now inserted in it. Which of the following is incorrect?

1. The potential difference between the plates decreases K times.
2. The energy stored in the capacitor decreases K times.
3. The energy stored in the capacitor decreases K times.
4. The change on the capacitor is not conserved.

Answer: 4. The change on the capacitor is not conserved.

Let charge q on the capacitor (C) when connected to a cell of emf(V) is given by, q = CV

V=\(\frac{q}{C}\)

Energy stored is, U=\(\frac{1}{2} C V^2=\frac{q^2}{2 C}\)

When a dielectric slab of dielectric constant K is inserted, then a new capacitor \(C^{\prime}\) will be

V=\(\frac{q}{C^{\prime}}=\frac{q}{C K}\)

And energy stored is, \(U^{\prime}=\frac{q^2}{2 C K}\)

⇒ \(\Delta U=U-U\)

= \(\frac{q^2}{2 C}\left(\frac{1}{K}-1\right)\)

= \(\frac{1}{2} C V^2\left(\frac{1}{K}-1\right)\)

Question 51. The energy required to charge a parallel plate condenser of plate separation d and plate area of cross-section A such that the uniform electric field between the plates is E is:

1. \(\frac{1}{2} \frac{\varepsilon_0 E^2}{A d}\)
2. \(\frac{\varepsilon_0 E^2}{A d}\)
3. \(\varepsilon_0 E^2 A d\)
4. \(\frac{1}{2} \varepsilon_0 E^2 A d\)

Answer: 3. \(\varepsilon_0 E^2 A d\)

The energy given to the cell, E=\(C V^2\)

Where, C= capacitance of conductor =\(\frac{A \varepsilon_0}{d}\)

V= potential difference across the plate

E =\(\left(\frac{A \varepsilon_0}{d}\right)(E d)^2\)

=A \(\varepsilon_0 E^2 d\)

Question 52. Two condensers, one of capacity C and the other of capacity C/2 are connected to an F-volt battery, as shown. The work done in charging fully both the condensers is:

1. \(\frac{1}{4} \mathrm{CV}^2\)
2. \(\frac{3}{4} C V^2\)
3. \(\frac{1}{2} C V^2\)
4. \(2 \mathrm{CV}^2\)

Answer: 2. \(\frac{3}{4} C V^2\)

Work done in charging fully both the condensers,

⇒ \(\mathrm{W}=\mathrm{U}=\frac{1}{2} C V^2+\frac{1}{2}\left(\frac{C}{2}\right) V^2\)

v \(\mathrm{~W}=\mathrm{U}=\frac{3}{4} C V^2\)

Question 53. A capacitor is charged by connecting a battery across its plates. It stores energy U. Now the battery is disconnected and another identical capacitor is connected across it, then the energy stored by both capacitors of the system will be:

1. U
2. \(\frac{U}{2}\)
3. 2U
4. \(\frac{3}{2} U\)

Answer: 2. \(\frac{U}{2}\)

The initial energy held in a capacitor is released when it is charged by connecting a battery across its plates.\(U=\frac{q^2}{2 C}\)

The charge remains constant when the battery is disconnected, i.e. q = constant. Now, another identical capacitor is connected across it, forming a parallel connection. Thus, the equivalent capacitance.

⇒ \(C_{e q} =C_1+C_2 \)

=C+C=2 C

Final energy stored by the system of capacitors,

⇒ \(U^{\prime}=\frac{q^2}{2 C_{\mathrm{eq}}}\)

⇒ \(U^{\prime}=\frac{q^2}{2(2 \mathrm{C})}\)

⇒ \(U^{\prime}=\frac{1}{2} U \)

∴ \(U^{\prime}=\frac{1}{2} U\)

Question 54. If the potential of a capacitor having a capacity of 6μF is increased from 10 V to 20 V, then the increase in its energy will be:

1. 4 \(\times 10^{-4} \mathrm{~J}\)
2. 4 \(\times 10^{-4} \mathrm{~J}\)
3. 9 \(\times 10^{-4} \mathrm{~J}\)
4. 12 \(\times 10^{-4} \mathrm{~J}\)

Answer: 3. 9 \(\times 10^{-4} \mathrm{~J}\)

Energy is stored in the dielectric medium between the plates of a charged capacitor in the form of electric field energy. The energy stored in the capacitor is determined by \(U=\frac{1}{2} C V^2\)

If the initial and the final potential are \(v_1 v_2\) respectively,

then increase in energy \((\Delta U)\),

⇒ \(\Delta U =\frac{1}{2} C\left(C_2^2-V_1^2\right)\)

= \(\frac{1}{2} \times(6 \times 10^{-6}) \times[(20)^2-(10^2]\)

= \(\frac{1}{2}\left(3 \times 10^{-6}\right) \times 300=9 \times 10^{-4} \mathrm{~J}\)

Electric Charges And Field

Question 1. Two point charges A and B having charges + Q and – Q respectively, are placed at a certain distance apart and force acting between them in F. If 25% of charges of A is transferred to B, then the force between the charges becomes

1. \(\frac{9 F}{16}\)
2. \(\frac{16 F}{9}\)
3. \(\frac{4 F}{3}\)
4. F

Answer: 1. \(\frac{9 F}{16}\)

We can write from the given question,

F= \(k \frac{Q^2}{r^2}\)

If 25% of the charge of A transferred to B then,

⇒ \(q_{\mathrm{A}}=Q-\frac{Q}{4}=\frac{3 Q}{4}\)

and \(q_B=-Q+\frac{Q}{9}=\frac{-3 q}{4}\)

⇒ \(F_1=\frac{K q_{\mathrm{A}} q_{\mathrm{B}}}{r^2}\)

⇒ \(F_1=\frac{K\left(\frac{3 Q}{4}\right)^2}{r^2}=\frac{9}{16} \frac{K Q}{r^2}\)

∴ \(F_1=\frac{9 F}{16}\) .

Question 2. Suppose the charge of a proton and an electron differ slightly. One of them is e and the other is (e + Δe). If the net electrostatic force and the gravitational force between two hydrogen atoms placed at a distance d (much greater than atomic size) apart are zero, then Ae is of the order [Given the mass of hydrogen if, m_h = 1.67 x 10^-27 kg]:

1. 10^-20C
2. 10^-23C
3. 10^-37C
4. 10^-47C

Answer: 3. 10^-37C

Read and Learn More NEET Physics MCQs

Here gravitational attractive force between two H-atoms is \(F_G=\frac{G m^2}{d^2}\)  → Equation 1

and electrostatic repulsive force between two H-atom is \(F_e=\frac{K q^2}{d^2}=\frac{K(\Delta e)^2}{d^2}\) →  Equation 2

Thus we have, \(\frac{K(\Delta e)^2}{d^2}=\frac{G m^2}{d^2}\)

⇒ \(9 \times 10^9(\Delta e)^2=6.67 \times 10^{-11} \times 1.67 \times 10^{-27} \times 1.67 \times 10^{-27}\)

⇒ \((\Delta e)^2=\frac{6.67 \times 1.67 \times 1.07}{9} \times 10^{-74}\)

∴ \(\Delta e=1.437 \times 10^{-37} \mathrm{C}\)

Question 3. Two identical charged spheres suspended from a common point by two massless strings of lengths /, are initially at a distance d (d < 1) apart because of their mutual repulsion. The charges begin to leak from both spheres at a constant rate. As a result, the spheres approach each other with a velocity v. Then, v varies as a function of the distance x between the spheres, as:

1. v \(\propto x^{-1 / 2}\)
2. v \(\propto x^{-1}\)
3. v \(\propto x^{-1}\)
4. v \(\propto x^{1 / 2}\)

Answer: 2. v \(\propto x^{-1}\)

From the diagram,

⇒ \(\tan \theta=\frac{F_e}{m g}=\theta\)

⇒ \(\frac{K q^2}{x^2 m g}=\frac{x}{2 l}\)

or \(x^3 \propto q^2\) →  Equation 1

or \(x^{3 / 2} \propto q\) →  Equation 2

differential eq. (1) w.r.t. to time,

⇒ \(3 x^2 \frac{d x}{d t} \propto 2 q \frac{d q}{d t}\)

but \(\frac{d q}{d t}\) is constant.

So \(x^2(v) \propto q \)replace q from eq. (2),

⇒ \(x^2(v) \propto x^{3/2}\)

∴ \(v \propto x^{+1 / 2}\)

Question 4. Two pith balls carrying equal charges are suspended from a common point by strings of equal length, the equilibrium separation between them is r. Now the strings are rigidly damped at half the height. The equilibrium separation between the balls now becomes.

1. \(\left(\frac{1}{\sqrt{2}}\right)^2\)
2. \(\left(\frac{r}{\sqrt[3]{2}}\right)\)
3. \(\left(\frac{2 r}{\sqrt{3}}\right)\)
4. \(\left(\frac{2 r}{3}\right)\)

Answer: 2. \(\left(\frac{r}{\sqrt[3]{2}}\right)\)

Here, \(\tan \theta =\frac{F}{m g}\)

⇒ \(\frac{r}{y} =\frac{k q^2}{r^2 m g}\)

⇒ \(y \propto r^3\)

⇒ \(\left(\frac{r^1}{r}\right)^3=\frac{y / 2}{y}\)

∴ \(r^1=r\left(\frac{1}{2}\right)^{1 / 3}\)

Question 5. A charge ‘q’ is placed at the centre of the line joining two equal charges ‘Q. The system of three charges will be in equilibrium if ‘q’ is equal to:

1. -S/4
2. g/4
3. – e/2
4. e/2

Answer: 1. -S/4

According to the question,

for equilibrium, the net force on charge p = 0

⇒ \(\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{Q} q}{r^2}+\frac{1}{4 \pi \epsilon_0} \cdot\)

⇒ \(\frac{\mathrm{Q}^2}{\left(\frac{r}{2}\right)^2}\)=0

⇒ \(\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{Q}^2}{r^2} =-\frac{1}{4 \pi \epsilon_0} \frac{4 \mathrm{Q} q}{r^2}\)

Q=-4 q

q = \(-\frac{Q}{4}\)

Question 6. Two positive ions, each carrying a charge q, are separated by a distance d. If F is the force of repulsion between the ions, the number of electrons missing from each ion will be (e being the charge on an electron):

1. \(\frac{4 \pi \varepsilon_0 F d^2}{e^2}\)
2. \(\sqrt{\frac{4 \pi \varepsilon_0 F e^2}{d^2}}\)
3. \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)
4. \(\frac{4 \pi \varepsilon_0 F d^2}{q^2}\)

Answer: 3. \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)

The force of repulsion between them is,

F=\(k \frac{q q}{d^2}=\frac{1}{4 \pi \varepsilon_0} \frac{q q}{d^2}\)  → Equation 1

Here, q = ne

F= \(\frac{1}{4 \pi \varepsilon_0} \frac{(n e)(n e)}{d^2}\)

n= \(\sqrt{\frac{4 \pi \varepsilon_0 F d^2}{e^2}}\)

Question 7. The unit of permittivity of free space ε₀ is:

1. coulomb/newton-metre
2. newton-metre2/coulomb²
3. coulomb²/newton-metre²
4. coulomb²/(newton-metre)²

Answer: 3. coulomb²/newton-metre²

We know that, F =\(\frac{1}{4 \pi \varepsilon_0} \frac{q^2}{r^2}\)

∴ \(\varepsilon_0 =\frac{1}{4 \pi} \frac{a^2}{\mathrm{Fr} r^2}=\frac{\mathrm{C}^2}{\mathrm{~N}-\mathrm{m}^2}\)

Question 8. An electron is moving around the nucleus of a hydrogen atom in a circular orbit of radius r. The coulomb force \(\vec{F}\) between the two is \(\left(\text { where } K=\frac{1}{4 \pi \varepsilon_0}\right)\):

1. \(K \frac{e^2}{r^2} \hat{r}\)
2. -K \(\frac{e^2}{r^3} \hat{r}\)
3. -K \(\frac{e^2}{r^2} \hat{r}\)
4. K \(\frac{e^2}{r^3} \hat{r}\)

Answer: 4. K \(\frac{e^2}{r^3} \hat{r}\)

The charge on hydrogen nuclear \(q_1=+v e \)

Coulomb’s force, F =\( K \frac{q_1 q_2}{r^2}\)

= K \(\frac{(+e)(-e)}{r^2} \hat{r}=-\frac{k e^2}{r^2} \hat{r}\)

Question 9. When air is replaced by a dielectric medium of constant k, the maximum force of attraction between two charges, separated by a distance

1. decreases K times
2. increases AT times
3. remains uncharged
4. becomes – times

Answer: 1. decreases K times

According to Coulomb’s law, the force between two charges is directly proportional to the product of charges and inversely proportional to the square of the distance between them.

F=\(\frac{1}{4 \pi \varepsilon_0} \frac{q_1 q_2}{r^2}\)  → Equation 1

Where, \(\frac{1}{4 \pi \varepsilon_0}\) = proportionality constant

If a dielectric medium of constant K is placed between them, then, a new force between the charges will be,

⇒ \(F_1=\frac{1}{4 \pi \varepsilon_0 K} \frac{q_1 q_2}{r^2}\) →  Equation 2

Dividing Eq. (2) by (1), we get,

⇒ \(\frac{F_1}{F}=\frac{1}{k}\)

⇒ \(F^{\prime}=\frac{F}{k}\)

∴ Thus, the new force decreases K times.

Question 10. An electron falls from rest through a vertical distance h in a uniform and vertically upward-directed electric field E. The direction of the electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall of the proton is:

1. 10 times greater
2. 5 times greater
3. smaller
4. equal

Answer: 3. smaller

Consider, the force on a charged particle in an electric field is: F = qE

And from Newton’s 2 \( { }^{\text {nd }}\) law of motion,

F = ma

From the above two equations,

qE = ma

a =\(\frac{q E}{m}\)  → Equation 1

Now consider that particle falls from rest means u=0 and s=h

S= \(u t+a t^2 \)

h= \(\frac{1}{2} a t^2\)

h= \(\frac{1}{2}\left(\frac{q E}{m}\right)^{t^2}\)

h= \(\frac{1}{2} \frac{q E}{m} t^2\)

t= \(\sqrt{\frac{2 h m}{q E}}\)

Question 11. The electric field in a certain region is acting radially outward and is given by E = Ar. A charge contained in a sphere of radius ‘a’ centred at the origin of the field’ will be given by:

1. \(4 \pi \varepsilon_0 A a^2\)
2. A \(\varepsilon_0 a^2\)
3. 4 \(\pi \varepsilon_0 A a^3\)
4. \(\varepsilon_0 A a^3\)

Answer: 3. 4 \(\pi \varepsilon_0 A a^3\)

From eq.(1)\( t \propto \sqrt{m}\) a q is the same for electron and proton.

Since an electron has a smaller mass it will take less time.

Question 12. The electric field at a distance \(\frac{3 R}{2}\) from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance \(\frac{R}{2}\) from the centre of the sphere is:

1. zero
2. E
3. \(\frac{E}{2}\)
4. \(\frac{E}{3}\)

Answer: 1. zero

We know that the electric field inside the conductor is zero. So, the electric field at a distance \(\frac{R}{2}\) from the centre of the sphere will also be zero.

Question 13. A particle of mass m and charge q is placed at rest in a uniform electric field E and then released. The kinetic energy attained by the particle after moving a distance y is:

1. \(q E y^2\)
2. \(q E^2 y\)
3. \(q E y\)
4. \(q^2 E y\)

Answer: 3. \(q E y\)

We have, electric force on a charged particle, F = qE

Mechanical on a charged particle in a uniform electric field is, F = ma = Eq

a = \(\frac{q E}{m}\)

From the equation of motion, we get,

⇒ \(v^2 =u^2+2 a y \)

a =\(\frac{q E}{m}\)

= \(\frac{2 q E \mathrm{y}}{m}\)

⇒ \(\ldots[\mathrm{u}=0]\)

Now, kinetic energy of the particle, k =\(\frac{1}{2} m v^2 \)

= \(\frac{m}{2} \times \frac{2 q E \mathrm{y}}{m}=q E y\)

Question 14. A square surface of side Z metre in the plane of the paper is placed in a uniform electric field E (volt/m) acting along the same place at an angle θ with the horizontal side of the square as shown in the figure. The electric flux linked to the surface in a unit of V-m is

1. \(E L^2\)
2. \(E L^2 \cos \theta\)
3. \(E L^2 \sin \theta\)
4. 0

Answer: 4. 0

We know that, flux, \(\phi =\vec{E} \cdot \vec{A}\)

= E A \(\cos \theta=\vec{E} \cdot \vec{A}\)

And \(\vec{E} \cdot \vec{A}\)=0 then lines are parallel to the surface.

Question 15. A square surface of side L metres is in the plane of the paper. A uniform electric field \(\vec{E}\)(volt/m), also in the plane of the paper, is limited only to the lower half of the square surface (see figure). The electric flux in SI units associated with the surface is:

1. \(E L^2\)
2. \(E L^2 / 2 \varepsilon_{\mathrm{o}}\)
3. \(E L^{2 / 2}\)
4. zero

Answer: 4. zero

Electric flux \(\phi_E =\int \vec{E} \cdot \overrightarrow{d s}=\int E d s \cos \theta\)

= \(\int E d s \cos 90^{\circ}\)=0

Question 16. Two point charges -q and +q are placed at a distance of L, as shown in the figure. The magnitude of electric field intensity at a distance R (R > >L) varies as:

1. \(\frac{1}{\mathrm{R}^2}\)
2. \(\frac{1}{\mathrm{R}^3}\)
3. \(\frac{1}{\mathrm{R}^4}\)
4. \(\frac{1}{\mathrm{R}^6}\)

Answer: 2. \(\frac{1}{\mathrm{R}^3}\)

The electric field due to a dipole at any arbitrary point (R, Q) is

⇒ \(\mathrm{E}=\frac{p}{4 \pi \varepsilon_0 R^3} \sqrt{3 \cos ^2 \theta+1}\)

⇒ \(\mathrm{E} \propto \frac{1}{\mathrm{R}^3}\) .

∴ Here, \(\mathrm{E} \propto \frac{1}{\mathrm{R}^3}\).

Question 17. Polar molecules are the molecules:

1. having zero dipole moment.
2. acquire a dipole moment only in the presence of an electric field due to the displacement of charges.
3. acquire a dipole moment only when the magnetic field is absent.
4. having a permanent electric dipole moment.

Answer: 4. having a permanent electric dipole moment.

Polar molecules are molecules having a permanent electric dipole moment.

Question 18. The electric field at a point on the equatorial plane at a distance r from the centre of a dipole having dipole moment P is given by (r > > separation of two charges forming the dipole \(\varepsilon_0\) = permittivity of free space):

1. \(\frac{-P}{4 \pi \varepsilon_0 r^3}\)
2. \(\frac{2 P}{4 \pi \varepsilon_0 r^3}\)
3. \(-\frac{P}{4 \pi \varepsilon_0 r^2}\)
4. \(\frac{P}{4 \pi \varepsilon_0 r^2}\)

Answer: 1. \(\frac{-P}{4 \pi \varepsilon_0 r^3}\)

Electric field due to an electric dipole at an equatorial plane at a distance r from the centre of the dipole is given by:

⇒ \(E_e=\frac{q(2 a)}{4 \pi \varepsilon_0\left(r^2+a^2\right)^{3 / 2}}\)

Directed from Q to R,

⇒ \(E_e=-\frac{P}{4 \pi \varepsilon_0\left(r^2+a^2\right)^{\frac{3}{2}}}\)

For a very short dipole (a < < r),

∴ \(E_e=-\frac{P}{4 \pi \varepsilon_0 r^3}\)

Question 19. Three point charges +q, -2q and +q are placed at points (x = 0, y = a, z = 0), (x = 0, y = 0, z = 0) and (x = a, y = 0, z = 0) respectively. The magnitude and direction of the electric dipole moment vector of this charge assembly are:

1. \(\sqrt{2}\) q a along the line joining points (x=0, y=0, z=0) and (x=a, y=a, z=0)
2. q a along the line joining points (x=0, y=0, z=0) and (x=a, y=a, z=0)
3. \(\sqrt{2}\) q a along +x direction
4. \(\sqrt{2}\) q a along +y direction

Answer: 1. \(\sqrt{2}\) q a along the line joining points (x=0, y=0, z=0) and (x=a, y=a, z=0)

This consists of two dipoles, – q and +4 with dipole moment along with the +y direction and q and +q along the X-direction.

The resultant moment ,=\(\sqrt{q^2 a^2+q^2 a^2}\) = \(\sqrt{2} q a\)

Along the direction 45″ that is along OP where P is (+a, a,0)

Question 20. The formation of the dipole is due to two equal and dissimilar point charges placed at a:

1. short distance
2. long distance
3. above each other
4. None of these

Answer: 1. short distance

A pair of equal and opposite point charges separated by a small distance form an electric dipole. Electric dipoles are atoms or molecules of ammonia, water alcohol, carbon dioxide, HCl, and other compounds in which the centres of positive and negative charge distributions are separated by a small distance

Question 21. The intensity of an electric field (E) depends on distance r due to a dipole, is related to:

1. E\( \propto \frac{1}{r}\)
2. E \(\propto \frac{1}{r^2}\)
3. E \(\propto \frac{1}{r^3}\)
4. E \(\propto \frac{1}{r^4}\)

Answer: 3. E \(\propto \frac{1}{r^3}\)

On the axial line of an electric dipole, the field intensity is given by E=\(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 p}{r^3}\)  → Equation 1

Electric field at equatorial position, E=\(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{p}{r^3}\) →  Equation 2

where. p is electric dipole moment,

From (1) and (2), we get E \(\propto \frac{1}{\mathrm{r}^3}\)

Question 22. An electric dipole is placed at an angle of 30° with an electric field intensity of 2 x 10⁵ N/C. It experiences a torque equal to 4 Nm. The charge on the dipole. If the dipole length is 2 cm is:

1. 8 mC
2. 2 mC
3. 5 mC
4. 7μC

Answer: 2. 2 mC

We know that the Torque in an electric dipole is

⇒ \(\vec{\tau}=\vec{P} \times \vec{E}\)

⇒ \(|\tau| =P E \sin \theta\)

We can write, \(\tau=q 2 l E \sin \theta=q \times 2 l \times E \sin \theta\)

putting the given values we have, 4 =q \(\times 2 \times 2 \times 10^{-4} \times 2 \times 10^5 \times \sin 30^{\circ}\)

q =2 \(\times 10^{-3} \mathrm{C}=2 \mathrm{mC}\)

Question 23. A spherical conductor of radius 10 cm has a charge of 3.2 x 10^-7 distributed uniformly. What is the magnitude of the electric field at a point 15 cm from the centre of the Sphere \(\left(\frac{1}{4 \pi \varepsilon_0}=9 \times 10^9 \mathrm{Nm}^2 / \mathrm{C}^2\right)\)

1. \(1.28 \times 10^5 \mathrm{~N} / \mathrm{C}\)
2. 1.28 \(\times 10^6 \mathrm{~N} / \mathrm{C}\)
3. 1.28 \(\times 10^7 \mathrm{~N} / \mathrm{C}\)
4. 1.28 \(\times 10^4 \mathrm{~N} / \mathrm{C}\)

Answer: 1. \(1.28 \times 10^5 \mathrm{~N} / \mathrm{C}\)

Given: r=10 \(\mathrm{~cm}=10 \times 10^{-2} \mathrm{~m}\)

Charge, q=3.2 \(\times 10^{-7} \mathrm{C}\)

The electric field at a point (x=15 cm ) from the centre of the sphere is:

⇒ \(\mathrm{E} =\frac{1}{4 \pi \varepsilon_0} \frac{q}{x^2}\)

= \(9 \times 10^9 \times \frac{3.2 \times 10^{-7}}{225 \times 10^{-4}}\)

= \(1.28 \times 10^5 \mathrm{~N} / \mathrm{C}\) .

Question 24. A thin conducting ring of radius R is given a charge + Q. The electric field at the centre O of the ring due to the charge on the part AKB of the ring is E. The electric field at the centre due to the charge on the part ACDB of the ring is:

1. 3 E along KO
2. 3 along OK
3. E along KO
4. 3 E along OK

Answer: 2. 3 along OK

The electric field due to the given charged ring is zero at centre O. So electric field due to AKB is equal and opposite to the electric field due to ACDB, from the principle of superposition. Since \(\overrightarrow{\mathrm{E}}\) is field strength, of O along \(\overrightarrow{K O}\) . So electric field strength due to ACDB along \(\overrightarrow{O K}\) and it is equal to E.

Question 25. The electric field strength in air at NTP is 3 x 10⁸ V/m. The maximum charge that can be given to a spherical conductor of radius 3 m is:

1. 3 x 10⁴ C
2. 3 x 10^-3 C
3. 3 x 10^-2 C
4. 3 x 10^-1 C

Answer: 2. 3 x 10^-3 C

Given, \(E_{\max }=3 \times 10^6 \mathrm{~V} / \mathrm{m}\) and R=3 \(\mathrm{~m}\) We have,

E =\(\frac{1}{4 \pi \varepsilon_0} \times \frac{Q}{R^2}\)

⇒ \(Q_{\max } =4 \pi \varepsilon_0 R^2 E_{\max }\)

=\(\frac{3 \times 3 \times 3 \times 10^6}{9 \times 10^9}\)

=3 \(\times 10^{-3} \mathrm{C}\)

Question 26. Two spherical conductors A and B of radii 1 mm and 2 mm are separated by a distance of 5 cm and are uniformly charged. If the spheres are connected by a conducting wire then in equilibrium condition, the ratio of the magnitude of the electric fields at the surfaces of spheres A and B is:

1. 4:1
2. 1:2
3. 2:1
4. 1:4

Answer: 1. 4:1

When a conducting wire connects two conducting spheres, charge flows from one sphere (with a higher potential) to the other (with a lower potential) until both spheres have the same potential.

E=\(\frac{1}{4 \pi \varepsilon_0} \times \frac{q}{r^2}\)

So, for different cases, \(\frac{E_1}{E_2}=\left(\frac{r_2}{r_1}\right)^2\)=4: 1

Question 27. A sphere encloses an electric dipole with charge \(\pm 3 \times 10^{-6} \mathrm{C}\). What is the total electric flux across the sphere?

1. \(-3 \times 10^{-6} \mathrm{~N}-\mathrm{m}^2 / \mathrm{C}\)
2. zero
3. \(3 \times 10^6 \mathrm{~N}-\mathrm{m}^2 / \mathrm{C}\)
4. \(6 \times 10^{-6} \mathrm{~N}-\mathrm{m}^2 / \mathrm{C}\)

Answer: 2. zero

From the figure it is clear that the sphere is enclosed a change is q= \(\pm 3 \times 10^{-6} \mathrm{C}\) which means it is a dipole.

We know that,Flux, \(\phi=\frac{(\text { Charge })_{\text {inside }}}{\epsilon_0}=\frac{q_{\text {in }}}{\epsilon_0}\)

Here total charge inside the sphere is zero.

⇒ \(\phi=\frac{0}{\epsilon_0}\)=0

The charge enclosed is zero.

The total electric flux is zero.

Question 28. A charge Q is enclosed by a Gaussian spherical surface of radius R. If the radius is doubled, then the outward electric flux will:

1. be reduced to half
2. remain the same
3. be doubled
4. increases four times

Answer: 2. remain the same

⇒ \(\phi_{\text {net }}=\frac{\Sigma q}{\varepsilon_0}\)

Net flux does not depend on the size of the Gaussian surface.

So, Flux remain unchanged

Question 29. A hollow cylinder has a charge q coulomb within it. If \(\phi\) is the electric flux in units of voltmeter associated with the curved surface B, the flux linked with the plane surface A in units of voltmeter will be:

1. \(\frac{q}{2 \varepsilon_0}\)
2. \(\frac{\phi}{3}\)
3. \(\frac{q}{\varepsilon_0}-\phi\)
4. \(\frac{1}{2}\left(\frac{q}{\varepsilon_0}-\phi\right)\)

Answer: 4. \(\frac{1}{2}\left(\frac{q}{\varepsilon_0}-\phi\right)\)

Let \(\phi_A, \phi_B\) and \(\phi_C\) be the electric fuse linked with A, B and C.

According to Gauss theorem, \(\phi_{\mathrm{A}}+\phi_{\mathrm{B}}+\phi_{\mathrm{C}}=\frac{q}{\varepsilon_0}\)

since, \(\phi_{\mathrm{A}}=\phi_{\mathrm{C}}\)

2 \(\phi_{\mathrm{A}}+\phi_{\mathrm{B}}=\frac{q}{\varepsilon_0}\)

or \(2 \phi_{\mathrm{A}}=\frac{q}{\varepsilon_0}-\phi_{\mathrm{B}}\)

or \(2 \phi_{\mathrm{A}}=\frac{q}{\varepsilon_0}-\phi \quad\left\{\text { since } \phi_{\mathrm{B}}=\phi\right\}\)

Question 30. A charge q is located at the centre of a cube. The electric flux through any face is:

1. \(\frac{2 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)
2. \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)
3. \(\frac{\pi q}{6\left(4 \pi \varepsilon_0\right)}\)
4. \(\frac{-q}{6\left(4 \pi \varepsilon_0\right)}\)

Answer: 2. \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)

The electric flux through any face,

⇒ \(\phi_{\text {face }}=\frac{q}{\varepsilon_0}\)

= \(\frac{4 \pi q}{6\left(4 \pi \varepsilon_0\right)}\)

Question 31. A Charge q is placed at the corner of a cube of side a. The electric flux through the cube is:

1. \(\frac{q}{\varepsilon_0}\)
2. \(\frac{q}{3 \varepsilon_0}\)
3. \(\frac{q}{6 \varepsilon_0}\)
4. \(\frac{q}{8 \varepsilon_0}\)

Answer: 4. \(\frac{q}{8 \varepsilon_0}\)

According to Gauss law, the electric flux through a closed surface is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed by the surface.

since, q is the charge enclosed by the surface, then electric flux,q= \(\phi=\frac{1}{\varepsilon_0}\)

If charge q is placed in one of the cube’s corners, it will be divided into eight similar cubes.

Therefore, electric flux through the cube \(\phi^{\prime}=\frac{1}{8}\left(\frac{q}{\varepsilon_0}\right)\)

Question 32. A point charge + q is placed at the mid-point of a cube of side L. The electric flux emerging from the cube is:

1. \(\frac{q}{\varepsilon_0}\)
2. \(\frac{6 q L^2}{\varepsilon_0}\)
3. \(\frac{q}{6 L^2 \varepsilon_0}\)
4. zero

Answer: 1. \(\frac{q}{\varepsilon_0}\)

According to Gauss’s theorem, the total electric flux over a closed surface is \(\frac{1}{\varepsilon_0}\) times the total charges contained inside the surface.

Total electric flux =\(\frac{\text { Total charge inside cube }}{\varepsilon_0}\)

∴ \(\phi =\frac{\mathrm{q}}{\varepsilon_0}\)

Question 33. Two parallel infinite line charges with linear charge densities + \(\lambda\) C/m and – \(\lambda\), C/m is placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?

1. \(\frac{2 \lambda}{2 \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)
2. \(\frac{\lambda}{\pi \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)
3. \(\frac{\lambda}{2 \pi \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)
4. Zero

Answer: 2. \(\frac{\lambda}{\pi \varepsilon_0 R} \mathrm{~N} / \mathrm{C}\)

Electric field due to line charge (1), \(\vec{E}_1=\frac{\lambda}{2 \pi \varepsilon_0 R} \hat{i}\)

Electric field due to line charge (2),

⇒ \(\vec{E}_2 =\frac{\lambda}{2 \pi \varepsilon_0 R} \hat{i} \mathrm{~N} / \mathrm{C}\)

⇒ \(E_{\text {net }} =\vec{E}_1+\vec{E}_2\)

= \(\frac{\lambda}{2 \pi \varepsilon_0 \mathrm{R}} i+\frac{\lambda}{2 \pi \varepsilon_0 \mathrm{R}} \hat{i}\)

= \(\frac{\lambda}{\pi \varepsilon_0 \mathrm{R}} \hat{i} \mathrm{~N} / \mathrm{C}\)

Question 34. A hollow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:

1. zero as increases for r < R_i decreases as r increases for r > R
2. zero as r increases for r < rR_i increases as r increases for r > R
3. decreases as r increases for r < R and for r > R
4. increases as r increases for r < R and for r > R

Answer: 1. Zero as increases for r < Ri decreases as r increases for r > R

Charge Q will be distributed over the surface of a hollow metal sphere.

(1) For \(\mathrm{r}<\mathrm{R}(inside)\)

By gauss law \(\oint \overrightarrow{E_{1 \mathrm{n}}} \cdot \overrightarrow{d \mathrm{~s}}=\frac{q_{e n}}{\varepsilon_0}\)

∴ \(E_{\text {in }}=0 (q_{\text {en }}=0)\)

(2) For r>R (outside)

⇒ \(\oint \vec{E}_0 \cdot \overrightarrow{d s}=\frac{q_{e n}}{\varepsilon_0}\)

Here \(q_{\text {en }}\)=0

⇒ \(\left(q_{e n}=\mathrm{Q}\right)\)

For \(r>R,\vec{E}_0=\frac{1}{4 \pi \varepsilon_0} \frac{Q}{\left|\vec{R}^2\right|} \hat{r}\)

⇒ \(E_0 \propto \frac{1}{r^2}\)

∴ \(\vec{E}_0\) decreases

Waves

Question 1. Which one of the following statements is true?

1. Both light and sound waves can travel in a vacuum
2. Both light and sound waves in air are transverse
3. The sound waves in air are longitudinal while the light waves are transverse
4. Both light and sound waves in air are longitudinal

Answer: 3. The sound waves in air are longitudinal while the light waves are transverse

The sound waves in air are longitudinal while the light waves are transverse

Question 2. A wave travelling in the positive x-direction having displacement along 7-direction as 1 m, wavelength \(2 \pi \mathrm{m}\) and frequency of \(\frac{1}{\pi} H z\) is represented by:

1. \(y=\sin (x-2 t)\)
2. \(y=\sin (2 \pi x-2 \pi t)\)
3. \(y=\sin (10 \pi x-20 \pi t)\)
4. \(y=\sin (2 \pi \mathrm{x}-2 \pi t)\)

Answer: 1. \(y=\sin (x-2 t)\)

According to Question, A =\(1 \mathrm{~m} \)

y =A \(\sin (k x-\omega t)\)

= \(\sin \left(\frac{2 \pi}{2 \pi} x-2 \pi \times \frac{1}{\pi} t\right)\)

= \(\sin (x-2 t)\)

Question 3. Two waves are represented by the equations \(y_1=a \sin (\omega t+k x+0.57) \mathrm{m}\) and \(y_2=a \cos (\omega t+k x) \mathrm{m}\), where x in metre and t in second. The phase difference between them is:

1. 1.25 rad
2. 0.57 rad
3. 1.57 rad
4. 1.0 rad

Answer: 4. 1.0 rad

It is given that, \(y_1=A \sin (\omega t+k x+0.57) \mathrm{m}\)  →  Equation 1

and \(y_2=A \cos (\omega t+k x) \mathrm{m}\)

⇒ \(y_2=A \sin \left(\frac{\pi}{2}+\omega t+k x\right) \mathrm{m}\)  → Equation 2

Thus from these two equations, \(\Delta \phi =\phi_2-\phi_1\)

= \(\frac{\pi}{2}-0.57\)

=1.57-0.57=1 \(\mathrm{rad}\)

Read and Learn More NEET Physics MCQs

Question 4. A wave in a string has an amplitude of 2 cm. The wave travels in the + x direction with a speed of 128 ms^-1 and it is noted that 5 complete waves fit in the 4 m length of the string. The equation describing the wave is:

1. y= (0.02)m sin(7.85x + 1005t)
2. y = (0.02)m sin (15.7x- 2010t)
3. y = (0.02)m sin(15.7x + 2010t)
4. y = (0.02)m sin (7.85x + 1005t)

Answer: 4. 7 = (0.02)m sin (7.85x + 1005t)

According to the question, A =2 \(\mathrm{~cm}\) and

Direction  =+x direction

v =128 \(\mathrm{~ms}^{-1}\)

k =\(\frac{2 \pi}{\lambda}=\frac{2 \pi \times 5}{4}=7.85\)

And v =\(\frac{\omega}{k}=128 \mathrm{~ms}^{-1}\)

⇒ \(\omega =v \times k=128 \times 7.85=1005\)

y =\(A \sin (k x-\omega t) \)

becomes y =2 \(\sin (7.85 x-1005 t)\)

= (0.02) m \(\sin (7.85 x-1005 t)\)

Question 5. The wave described by y = \(y=0.25 \sin (10 \pi x-2 \pi t)\), where x and y are in metres and t in second, is a wave travelling along the:

1. – ve x – direction with frequency 1 Hz
2. + ve x – direction with frequency π Hz and wavelength λ = 0.2m
3. + ve x – direction with frequency 1 Hz and wavelength λ = 0.2 m
4. + ve x – direction with amplitude 0.25 m and wavelength λ = 0.2 m

Answer: 3. + ve x – direction with frequency 1 Hz and wavelength A = 0.2 m

Given,  y=0.25\( \sin (10 \pi x-2 \pi t)\)

comparing with equation of wave, y =A \(\sin (k x-\omega t)\)

A=0.25, k =10\( \pi, \omega=2 \pi\)

⇒ \(\frac{2 \pi}{\lambda} =10 \pi\),

2\( \pi f =10 \pi \)

f =5 \(\mathrm{~Hz}\)

⇒ \(\lambda =\frac{1}{5}=0.2 \mathrm{~m}\)

When signs of the coefficient of t and x are opposite it means

⇒ \(\frac{d x}{d t}=v>0\)

i.e. wave is propagating in the direction growing x.

Question 6. A wave travelling in the positive x-direction with amplitude A = 0.2 m, velocity V = 360 ms^-1 and wavelength λ = 60 m, then the correct expression for the wave is:

1. y=0.2 \(\sin \left[2 \pi\left(6 t+\frac{x}{60}\right)\right]\)
2. y=0.2 \(\sin \left[\pi\left(6 t+\frac{x}{60}\right)\right]\)
3. y=0.2 \(\sin \left[2 \pi\left(6 t-\frac{x}{60}\right)\right]\)
4. y=0.2 \(\sin \left[\pi\left(6 t-\frac{x}{60}\right)\right]\)

Answer: 3. y=0.2 \(\sin \left[2 \pi\left(6 t-\frac{x}{60}\right)\right]\)

The general equation of wave travelling in x-direction is given as

y=A \(\sin \left[\frac{2 \pi}{\lambda}(v t-x)\right]\)

Where, A=\(0.2 \mathrm{~m}, v=360 \mathrm{~ms}^{-1}, \lambda=60 \mathrm{~m}\)

The equation becomes, y=\(0.2 \sin \left[\frac{2 \pi}{60}(360 t-x)\right]\)

y=0.2 \(\sin \left[2 \pi\left(6 t-\frac{x}{60}\right)\right]\)

Question 7. If the initial tension on a stretched string is doubled then the ratio of the initial and final speeds of a transverse wave along the string is:

1. 1:1
2. \(\sqrt{2}: 1\)
3. 1: \(\sqrt{2}\)
4. 1: 2

Answer: 3. 1: \(\sqrt{2}\)

We know that the velocity of a transverse wave in a stretched string is, \(\mathrm{v}=\sqrt{\frac{T}{\mu}}\) →  Equation 1

Given = Tension, T = 27

Now, the speed of the wave in the string will be \(v^{\prime}=\sqrt{\frac{2 T}{\mu}}\)  → Equation 2

from eq (1) and (2), we get

∴ \(\frac{v}{v^{\prime}}=\frac{1}{\sqrt{2}}\)

Question 8. A uniform rope of length L and mass \(m_1\) hangs vertically from a rigid support. A block of mass \(m_2\) is attached to the free end of the rope. A transverse pulse wavelength \(\lambda_1\) is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the A rope is \(\lambda_2\). The ratio \(\frac{\lambda_2}{\lambda_1}\) is:

1. \(\sqrt{\frac{m_1+m_2}{m_2}}\)
2. \(\sqrt{\frac{m_2}{m_1}}\)
3. \(\sqrt{\frac{m_1+m_2}{m_1}}\)
4. \(\sqrt{\frac{m_1}{m_2}}\)

Answer: 1. \(\sqrt{\frac{m_1+m_2}{m_2}}\)

From the question: Wavelength of transverse pulse,

Also, we know that, \(\lambda=\frac{v}{n}\)  →  Equation 1

Also, we know that,

v= \(\sqrt{\frac{T}{\mu}}\)  →  Equation 2

v= velocity of the wave,

n= frequency of the wave

T= tension in the string

mu= mass per unit length of rope

From eq. (1) and (2), we get,

⇒ \(\lambda =\frac{1}{n} \sqrt{\frac{T}{\mu}}\)

⇒ \(\lambda \propto \sqrt{T}\)

∴ For different cases \(\frac{\lambda_2}{\lambda_1}=\sqrt{\frac{T_2}{T_1}}=\sqrt{\frac{m_1+m_2}{m_2}}\)

Question 9. The equation of a simple harmonic wave is given by:\(y=3 \sin \frac{\pi}{2}(50 t-x)\), where x and y are in metres and t is in seconds. The ratio of maximum particle velocity to the wave velocity is:

1. \(2 \pi\)
2. \(\frac{3}{2} \pi\)
3. 3 \(\pi\)
4. \(\frac{2}{3} \pi\)

Answer: 2. \(\frac{3}{2} \pi\)

We know that and \(v_{\max } =a \omega\)

v =\(n \lambda\)

⇒ \(\frac{v_{\max }}{v} =\frac{a \omega}{n \lambda}\)

= \(\frac{(2 \pi n) a}{n \lambda}=\frac{2 \pi a}{\lambda}\)

= \(\frac{2 \pi a}{\frac{2 \pi}{K}}=\frac{\pi}{2} \times 3=\frac{3 \pi}{2}\)

Question 10. Sound waves travel at 350 m/s through warm air at 3500 m/s through brass. The wavelength of a 700 Hz acoustic wave as it enters brass from warm air:

1. increases by a factor of 20
2. increases by a factor of 10
3. decreases by a factor of 20
4. decreases by a factor of 10

Answer: 2. increases by a factor of 10

Given, Velocity of ware in warm air \(v_1=350 \mathrm{~m} / \mathrm{s}\)

Velocity of ware in brass,\( v_2=3500 \mathrm{~m} / \mathrm{s}\)

We know that,Velocity of sound, v=\(n \lambda\)

⇒ \(\frac{v_1}{v_2}=\frac{n_1 \lambda_1}{n_2 \lambda_2}\)

Since, \(n_1=n_2 \)

\(\lambda_2=\lambda_1 \frac{v_2}{v_1}\)

=\(\lambda_1 \times \frac{3500}{350}\)

=\(\lambda_1 \times 10\)

⇒ \(\lambda_2=10 \lambda_1 \)

∴ \(\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}\)

Question 11. A transverse wave is represented by y =\(y=A \sin (\omega t-k x)\). For what value of the wavelength is the wave velocity equal to the maximum particle velocity?

1. \(\frac{\pi \mathrm{A}}{2}\)
2. \(\pi A\)
3. 2 \(\pi A\)
4. A

Answer: 3.

Wave velocity v=\(\frac{\omega}{K}=\omega A\)

⇒ \(\frac{\lambda}{2 \pi}\) =A

∴ \(\lambda =2 \pi A\)

Question 12. Two points are located at a distance of 10 m and 15 m from the source of oscillation. The period of oscillation is 0.05 s and the velocity of the wave is 300 m/s. What is the phase difference between the oscillation of two points?

1. \(\frac{\pi}{3}\)
2. \(\frac{2 \pi}{3}\)
3. \(\pi\)
4. \(\frac{\pi}{6}\)

Answer: 2. \(\frac{2 \pi}{3}\)

We know that, Phase-difference, \(\phi=\frac{2 \pi}{\lambda} \times\) path difference

Here path diff., \(\Delta x=15-10=5 \mathrm{~m}\)

Now frequency, v=\(\frac{1}{T}=\frac{1}{0.05}=20 \mathrm{~Hz}\)

velocity \(\mathrm{v}=300 \mathrm{~m} / \mathrm{s}\)

wavelength \(\lambda=\frac{\mathrm{v}}{\mathrm{v}}=\frac{300}{20}=15 \mathrm{~m}\)

Phase difference, \(\Delta \phi=\frac{2 \pi}{\lambda} \times x\)

= \(\frac{2 \pi}{15} \times 5=\frac{2 \pi}{3}\)

Question 13. A transverse wave propagating along the x-axis is represented by \(y(x, t)=8.0 \sin (0.5 \pi x-4 \pi t-\pi / 4)\) where x is in metres and t is in seconds. The speed of the wave is:

1. 8 \(\mathrm{~m} / \mathrm{s}\)
2. 4 \(\pi \mathrm{m} / \mathrm{s}\)
3. 0.5 \(\pi \mathrm{m} / \mathrm{s}\)
4. \(\frac{1}{2} \mathrm{~m} / \mathrm{s}\)

Answer: 1. 8 \(\mathrm{~m} / \mathrm{s}\)

It is given that, \(y(x, t)=8.0 \sin \left(0.5 \pi x-4 \pi t-\frac{\pi}{4}\right)\)

Compare this equation with the standard equation, we have,

y=\(A \sin \left(\frac{2 \pi x}{\lambda}-\frac{2 \pi t}{\mathrm{~T}}+\phi\right)\)

⇒ \(\frac{2 \pi}{\lambda} =0.5 \pi\)

⇒ \(\lambda =\frac{2 \pi}{0.5 \pi}=4 \mathrm{~m}\)

⇒ \(\frac{2 \pi}{T} =4 \pi\)

T =\(\frac{1}{2} \mathrm{~s}\)

∴ \(\mathrm{v}=\frac{\lambda}{T} =\frac{4}{1 / 2}=8 \mathrm{~m} / \mathrm{s}\)

Question 14. A point source emits sound equally in all directions in a non-absorbing medium. Two points P and Q are at distances of 2 m and 3 m respectively from the source. The ratio of the intensities of the wave at P and Q is:

1. 3:2
2. 2:3
3. 9:4
4. 4:9

Answer: 3. 9:4

Given: \(d_1=2 \mathrm{~m}_1, d_2=3 \mathrm{~m}\)

Intensity \(\propto \frac{1}{(\text { distance })^2}\)

⇒ \(I_1 \propto \frac{I}{2^2}\)

And, \(I_2 \propto \frac{1}{3^2}\)

∴ \(\frac{I_1}{I_2}=\frac{9}{4}\)=9: 4

Question 15. The equation of a wave is given by y = a sin\(\left(100 t-\frac{x}{10}\right)\) where x and y are in metres and t in seconds, then the velocity of the wave is:

1. 0.1 m/s
2. 10 m/s
3. 100m/s
4. 1000 m/s

Answer: 4. 1000 m/s

We have, y=A \(\sin \left(100 t-\frac{x}{10}\right)\)

On comparing with the standard wave equation, we get \(\omega=100, k=\frac{1}{10}\)

Velocity of the wave, \(\mathrm{v} =\frac{\omega}{k}=\frac{100}{1 / 10}\)

= \(100 \times 10=1000 \mathrm{~m} / \mathrm{s}\)

Question 16. If Cs be the velocity of sound in air and C be the RMS velocity, then

1. \(I_1+I_2\)
2. \(\left(\sqrt{I_1}+\sqrt{I_2}\right)^2\)
3. \(\left(\sqrt{I_1}-\sqrt{I_2}\right)^2\)
4. \(2\left(I_1+I_2\right)\)

Answer: 3. \(\left(\sqrt{I_1}-\sqrt{I_2}\right)^2\)

We have, velocity, \(C_s=\sqrt{\left(\frac{\gamma p}{\rho}\right)}\) →  Equation 1

where, p is pressure, \(\rho\) is density and \gamma[/latex] is atomicity of gas,

And RMS velocity of gas molecule, C=\(\sqrt{\left(\frac{3 p}{\rho}\right)}\) → Equation 2

From eq. (1) and (2), we get,

⇒ \(\frac{C_s}{C} =\sqrt{\frac{\gamma p}{\rho} \times \frac{\rho}{3 p}}=\sqrt{\frac{\gamma}{3}}\)

∴ \(C_s =C \times \sqrt{\frac{\gamma}{3}}\)

Question 17. Two periodic waves of intensities \(I_1\) and \(I_2\) pass through a region at the same time in the same direction. The sum of the maximum and minimum intensities is:

1. \(I_1+I_2\)
2. \(\left(\sqrt{I_1}+\sqrt{I_2}\right)^2\)
3. \(\left(\sqrt{I_1}-\sqrt{I_2}\right)^2\)
4. \(2\left(I_1+I_2\right)\)

Answer: 4. \(2\left(I_1+I_2\right)\)

I =\(I_1+I_2+2 \sqrt{I_1 I_2} \cos \phi \)

⇒ \(I_{\max } =\left(\sqrt{I_1}+\sqrt{I_2}\right)^2 \)

⇒ \(I_{\min } =\left(\sqrt{I_1}-\sqrt{I_2}\right)^2 \)

⇒ \(I_{\max }+I_{\min } =\left(\sqrt{I_1}+\sqrt{I_2}\right)^2+\left(\sqrt{I_1}-\sqrt{I_2}\right)^2 \)

= \(\left(I_1+I_2+2 \sqrt{I_1 I_2}\right)+\left(I_1+I_2-2 \sqrt{I_1 I}\right)\)

= \(2\left(I_2+I_2\right)\)

Question 18. Two waves of the same frequency and intensity superimpose on each other in opposite phases. After the superposition, the intensity and frequency of waves will:

1. increase
2. decrease
3. remain constant
4. become zero

Answer: 4. become zero

Sound and light are both altered by interference. In sound when the resultant intensity is maximum (in phase), the interference is said to be constructive and when the resultant intensity is minimum or zero, it is said to be destructive (in opposite phase).

Question 19. The length of the string of a musical instrument is 90 cm and has a fundamental frequency of 120 Hz. Where should it be pressed to produce a fundamental frequency of 180 Hz?

1. 75 cm
2. 60 cm
3. 45 cm
4. 80 cm

Answer: 2. 60 cm

Length of string of musical instrument = 90cm = 0.9m

fundamental frequency, \(f_1=120 \mathrm{~Hz}, f_2=180 \mathrm{~Hz}\) .

We know that: \(f \propto \frac{1}{l}\)

⇒ \(\frac{f_1}{f_2}=\frac{l_2}{l_1}\)

⇒ \(l_2=\frac{f_1}{f_2} \times l_1\)

⇒ \(l_2=\frac{120}{180} \times 0.9\)

⇒ \(l_2=\frac{2}{3} \times 0.9=0.6 \mathrm{~m}\)

∴ \(l_2=60 \mathrm{~cm} \text {. }\)

Question 20. A tuning fork with a frequency of 800 Hz produces resonance in a resonance column tube with the upper end open and the lower end closed by the water surface. Successive resonances are observed at lengths 9.75 cm, 31.25 cm and 52.75 cm. The speed of sound in air is:

1. 500 m/s
2. 156 m/s
3. 344 m/s
4. 172 m/s

Answer: 3. 344 m/s

The first and second resonance of the tuning fork of the resonance tube is shown below,

Here,\(l_1=\frac{\lambda}{4} and l_2=\frac{3 \lambda}{4}\)

⇒ \(l_2-l_1 =\frac{3 \lambda}{4}-\frac{\lambda}{4}=\frac{2 \lambda}{4}=\frac{\lambda}{2}\)

⇒ \(\lambda =2\left(l_2-l_1\right)\)

We know that,\( \mathrm{v} =f \lambda\)

⇒ \(\mathrm{v} =800 \times 2(31.25-9.75)\)

= 34400 \(\mathrm{~cm} / \mathrm{s}\)

∴ \(\mathrm{v} =344 \mathrm{~m} / \mathrm{s}\)

Question 21. The fundamental frequency in an open organ pipe is equal to the third harmonic of a closed organ pipe. If the length of the closed organ pipe is 20 cm, the length of the open organ pipe is:

1. 12.5 cm
2. 8 cm
3. 13.3 cm
4. 16 cm

Answer: 3. 13.3 cm

For closed organ pipe.

Third harmonics,\(f=\frac{3 V}{4 l}\)  →  Equation 1

Where f is the length of a closed organ pipe. for open organ pipe, fundamental frequency, \(f=\frac{V}{2 l^{\prime}}\)  →  Equation 2

Where I = length of the open organ pipe.

Equating equation (1) and (2)

⇒ \(\frac{3 \mathrm{~V}}{4 l}=\frac{\mathrm{V}}{2 l^{\prime}}\)

⇒ \(l^{\prime} =\frac{4 l}{3 \times 2}=\frac{2 l}{3}\)

⇒ \(l^{\prime} =\frac{2}{3} \times 20=\frac{40}{3}\)  [Since l = 20 given ]

=13.33 \(\mathrm{~cm}\)

Question 22. A tuning fork is used to produce resonance in a glass tube. The length of the air column in this tube can be adjusted by a variable piston. At room temperature of 27°C, two successive resonances are produced at 20 cm and 73 cm of column length. If the frequency of the tuning fork is 320 Hz, the velocity of sound in air at 27°C is:

1. 350m/s
2. 339 m/s
3. 330m/s
4. 300 m/s

Answer: 2. 339 m/s

For first resonance, \(l_1=\frac{\lambda}{4}\) and second resonance,\(l_2=\frac{3 \lambda}{4}\)

⇒ \(l_2-l_1 =\frac{3 \lambda}{4}-\frac{\lambda}{4}=\frac{\lambda}{2}\)

⇒ \(\lambda =2\left(l_2-l_1\right)\)

Velocity of sound wave

⇒ \(\mathrm{v}=\mathrm{v}\) (Where v= frequency)

⇒ \(\mathrm{v}=\mathrm{v}(2)\left(l_2-l_1\right)\)

⇒ \(\mathrm{v}\)=2[320(0.73-0.202)]

⇒ \(\mathrm{v}=2 \times 320 \times 0.53=339.2 \mathrm{~ms}^{-1}\)

∴ \(\mathrm{v}=339 \mathrm{~ms}^{-1}\)

Question 23. An air column, closed at one end and open at the other, resonates with a tuning fork when the smallest length of the column at 50 cm. The next larger length of the column resonating with the same tuning fork is:

1. 100cm
2. 150 cm
3. 200cm
4. 66.7 cm

Answer: 2. 150 cm

The situation is shown in the given diagram,

⇒ \(L_{\min } =\frac{\lambda}{4}\)

50 =\(\frac{\lambda}{4}\)

⇒ \(\lambda =200 \mathrm{~cm}\)

Next higher length of an column, L =\(\frac{\lambda}{4}+\frac{\lambda}{2}=\frac{3 \lambda}{4}\)

= \(\frac{3}{4} \times 200=150 \mathrm{~cm}\)

Question 24. The second overtone of an open organ pipe has the same frequency as the first overtone of a closed pipe L metre long. The length of the open pipe will be:

1. L
2. 2L
3. 1/2
4. 4L

Answer: 2. 2L

For second overtone (\( 3^{\text {rd }}\) harmonics) in open organ pipe,

⇒ \(\frac{3 \lambda}{2}=l_0\)

⇒ \(\lambda=\frac{2 l_0}{3}\)

for first overtone \(( 3^{\text {rd }}\) harmonics) in closed organ pipe ,

⇒ \(\frac{3 \lambda}{4} =l_c\)

⇒ \(\lambda =\frac{4 l_c}{3}=\frac{4 L}{3}\)

So, \(\frac{2 l_0}{3} =\frac{4 L}{3}\)

∴ \(l_0 =2 L\)

Question 25. The fundamental frequency of a closed organ pipe of length 20 cm is equal to the second overtone of an organ pipe open at both ends. The length of the organ pipe open at both ends is:

1. 80 cm
2. 100 cm
3. 120 cm
4. 140 cm

Answer: 3. 120 cm

For closed organ pipe, frequency of vibration \(f_c\) is given,

⇒ \(f_c=\frac{\mathrm{v}}{4 l}\)

l= length of closed organ pipe and for open organ pipe frequency of vibration is \(f_0\).

⇒ \(f_0=\frac{\mathrm{v}}{2 l}\),

l= length of open organ pipe

According to question, \(f_c =3 f_0\)

⇒ \(\frac{V}{4 l}=\frac{3 V}{2 l^{\prime}}\)

⇒ \(l^{\prime}\) =6 l

∴ \(l^{\prime}=6 \times 20=120 \mathrm{~cm}\)

Question 26. A string is stretched between fixed points separated by 75.0 cm. It is observed to have resonant frequencies of 420 Hz and 315 Hz. There are no other resonant frequencies between these two. The lowest resonant frequency for these strings is:

1. 155 Hz
2. 205 Hz
3. 10.5 Hz
4. 105 Hz

Answer: 4. 105 Hz

Two consecutive resonant frequencies for a string fixed at both ends will be, \(\frac{n \mathrm{v}}{2 l}\) and \(\frac{(n+1)}{2 l} \mathrm{v}\)

⇒ \(\frac{(n+1) \mathrm{v}}{2 l}-\frac{n \mathrm{v}}{2 l}\) =420-315

∴ \(\frac{\mathrm{v}}{2 l} =105 \mathrm{~Hz}\)

Question 27. If \(n_1, n_2 and n_3\) are the fundamental frequencies of three segments into which a string is divided, then the original fundamental frequency n of the string is given by:

1. \(\frac{1}{n}=\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}\)
2. \(\frac{1}{\sqrt{n}}=\frac{1}{\sqrt{n_1}}+\frac{1}{\sqrt{n_2}}+\frac{1}{\sqrt{n_3}}\)
3. \(\sqrt{n}=\sqrt{n_1}+\sqrt{n_2}+\sqrt{n_3}\)
4. n=\(n_1+n_2+n_3\)

Answer: 1. \(\frac{1}{n}=\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}\)

The string is divided into three points,

⇒ \(l_1\) has frequency \(n_1\)

⇒ \(l_2\) has frequency \(n_2\)

and \(l_3\) has frequency \(n_3\)

Using \(\mathrm{v} =f \lambda\)

⇒ \(\lambda =\frac{\mathrm{v}}{f}\)

⇒ \(l_1 =\frac{\mathrm{v}}{n_1}, l_2=\frac{\mathrm{v}}{n_2}, l_3=\frac{\mathrm{v}}{n_3}\)

⇒ \(l =l_1+l_2+l_3\)

⇒ \(\frac{\mathrm{v}}{n} =\frac{\mathrm{v}}{n_1}+\frac{\mathrm{v}}{n_2}+\frac{\mathrm{v}}{n_3}\)

where, \(\mathrm{v}\) is same in all case,

∴ \(\frac{1}{n}=\frac{1}{n_1}+\frac{1}{n_2}+\frac{1}{n_3}\)

Question 28. The number of possible natural oscillations of the air column in a pipe closed at one end of length 85 cm whose frequencies lie below 1250 Hz are (velocity of sound = 340 ms^-1):

1. 4
2. 5
3. 7
4. 6

Answer: 4. 6

For pipe closed at one end, \(f_n=n\left(\frac{v}{4 l}\right)\)

= \(n \times \frac{340}{4 \times 85 \times 10^{-2}}\) =100 n

⇒ \(f_1 =100 \mathrm{~Hz}\)

⇒ \(f_2 =300 \mathrm{~Hz}\)

⇒ \(f_3 =500 \mathrm{~Hz}\)

⇒ \(f_4 =700 \mathrm{~Hz}\)

⇒ \(f_5 =900 \mathrm{~Hz}\)

⇒ \(f_6 =1100 \mathrm{~Hz}\)

∴ This confirms that the number of possible natural oscillations could be 6.

Question 29. If we study the vibration of a pipe open at both ends, then the following statement is not true:

1. Open and will be anti-node.
2. Odd harmonics of the fundamental frequency will be generated.
3. All harmonics of the fundamental frequency will be generated.
4. Pressure change will be maximum at both ends.

Answer: 4. Pressure change will be maximum at both ends.

In the study of the vibration of a pipe open at both ends, the displacement node is the pressure antinode. So, the pressure change will be Maximum at the length \(\frac{1}{2}\) and the pressure variation will be minimum at both ends. The odd and even harmonics will be present in the vibration.

Question 30. The time of reverberation of room A is one second. What will be the time (in seconds) of reverberation of a room, having all the dimensions double those of room A?

1. 1
2. 2
3. 4
4. \(\frac{1}{2}\)

Answer: 2. 2

Reverberation Time, \(T=\frac{0.61 \mathrm{~V}}{\mathrm{~A} S}\)

Where, Z= Volume of room in cubic metres,4= Average absorption coefficient of the room S= Total surface area of the room in square metres

Clearly, T \(\propto \frac{V}{S}\)

⇒ \(\frac{T_1}{T_2} =\left(\frac{V_1}{V_2}\right)\left(\frac{S_2}{S_1}\right)\)

=\(\left(\frac{V}{8 V}\right)\left(\frac{4 S}{S}\right)=\frac{1}{2} \)

∴ \(T_2 =2 T_1=2 \times 1=2 \mathrm{~s}\) . \(( T_1=1 \mathrm{~s}\)

Question 31. Standing waves are produced in a 10 m-long stretched string. If the string vibrates in 5 segments and the wave velocity is 20 m/s, the frequency is:

1. 10 Hz
2. 5 Hz
3. 4 Hz
4. 2 Hz

Answer: 2. 5 Hz

For standing wave, the length of one segment will be \(\frac{\lambda}{2}\)}.

Since there are 5 segments and the total length of the string is 10 \(\mathrm{~m}\).

⇒ \(5 \times \frac{\lambda}{2}\) =10

⇒ \(\lambda =4 \mathrm{~m}\)

∴ Thus, frequency, n=\(\frac{\mathrm{v}}{\lambda}=\frac{20}{4}=5 \mathrm{~Hz}\mathrm{v}=20 \mathrm{~m} / \mathrm{s})\)

Question 32. Which one of the following is a simple harmonic motion?

1. Ball bouncing between two rigid vertical walls.
2. Particles move in a circle with uniform speed.
3. Wave moving through a string fixed at both ends
4. Earth spinning about its own axis

Answer: 3. Wave moving through a string fixed at both ends

In Simple harmonic motion, Individual particles of a medium execute simple harmonic motion about their mean position in a direction perpendicular to the direction of propagation of wave motion. SHM is performed by a wave travelling across a string with both ends fixed

Question 33. In a guitar, two strings A and B made of the same material are slightly out of tune and produce beats of a frequency of 6 Hz. When tension in B is slightly decreased, the beat frequency increases to 7 Hz. if the frequency of A is 530 Hz, the original frequency of B will be:

1. 524 Hz
2. 536 Hz
3. 537 Hz
4. 523 Hz

Answer: 1. 524 Hz

In the case of beat formation.

Unknown frequency \(v_B=v_A \pm\) beats

Where \(v_A=530 \mathrm{~Hz} \text {, beats }=6 \mathrm{~Hz}\)

⇒ \(v_B=530 \pm 6=536 \text {, or } 524 \mathrm{~Hz}\)

From the question, when tension is. B is slightly decreased, and then the beat frequency increases to 7 Hz. Thus the original frequency B is 524 Hz.

Question 34. Three sound waves of equal amplitudes have frequencies (n – 1), n, (n +1). They superimpose to give beats. The number of beats produced per second will be:

1. 1
2. 4
3. 3
4. 2

Answer: 4. 2

Now divide 1 second into 1,1,2, equal divisions

⇒ \(\frac{1}{1}, \frac{1}{1}, \frac{2}{1}\)

By eliminating common time instants, the total maxima in one second is 2.

Question 35. A source of unknown frequency gives 4 beats/s when sounded with a source of known frequency 250 Hz. The second harmonic of the source of unknown frequency gives five beats per second when sounded with the source of frequency 513 Hz. unknown frequency is:

1. 254 Hz
2. 246 Hz
3. 240 Hz
4. 260 Hz

Answer: 1. 254 Hz

Frequency of unknown source =246 Hz or 254 Hz

second harmonic of this source = 492Hz or 508 Hz

when given 5 beats per second when sounded with a source frequency of 513 Hz.

Therefore, unknown frequency = 254 Hz.

Question 36. Two identical piano wires kept under the same tension T have a fundamental frequency of 600 Hz. The fractional increase in the tension of one of the wires which will lead to the occurrence of 6 beat/s when both the wires oscillate together would be:

1. 0.02
2. 0.03
3. 0.04
4. 0.01

Answer: 1. 0.02

According To the Question, the Frequency of the string varies directly as the square root of its tension.

f \(\propto \sqrt{T}\)

⇒ \(\frac{\Delta f}{f} =\frac{1}{2} \cdot \frac{\Delta T}{T}\)

⇒ \(\frac{\Delta T}{T} =2 \cdot \frac{\Delta f}{f}\)

=2 \(\times \frac{6}{600}\)=0.02

Question 37. A tuning fork of frequency 512 Hz makes 4 beats/.? with the vibrating string of beats. The beat frequency decreases to 2 beats when the tension in the piano string is slightly increased. The frequency of the piano string before increasing the tension was:

1. 510 Hz
2. 514 Hz
3. 516 Hz
4. 508 Hz

Answer: 4. 508 Hz

We have, \(n_p \propto \sqrt{\mathrm{T}}\)

⇒ \(n_f\)= frequency of tuning fork =\(\frac{5}{2} \mathrm{~Hz} x\)= Beat frequency =4 beats

Hence, \(n_p-n_f=x \downarrow \text { (wrong) }\)

⇒ \(n_f-n_p=x \downarrow \text { (correct) }\)

∴ \(n_p=n_f-x=512-4=508 \mathrm{~Hz}\)

Question 38. Each of the two strings of length 51.6 cm and 49.1 cm are tensioned separately by 20 N force. The mass per unit length of both the strings is the same and equal to 1 gm1. When both the strings vibrate simultaneously the number of beats is:

1. 5
2. 7
3. 8
4. 3

Answer: 2. 7

According to the question, Frequency of first string, \(f_1=\frac{1}{2 l} \sqrt{\frac{T}{m}}\)

=\(\frac{1}{2 \times 51.6 \times 10^{-2}} \sqrt{\frac{20}{10^{-3}}}\)

=137.03 Hz

Frequency of second string,

⇒ \(f_2 =\frac{1}{2 \times 49.1 \times 10^{-2}} \sqrt{\frac{20}{10^{-3}}}\)

=144.01 Hz

Number of beats, \(f_2-f_1\)

= 144-137 = 7 beats

Question 39. Two sound waves with wavelengths 5.0 m and 5.5 m respectively, each propagate in a gas with a velocity of 330 m/s. We expect the following number of beats per second:

1. 6
2. 12
3. 0
4. 1

Answer: 1. 6

⇒ \(\text { Frequency }=\frac{\text { Velocity }}{\text { Wave length }}\)

⇒ \(v_1=\frac{\mathbf{v}}{\lambda_1}=\frac{330}{5}=66 \mathrm{~Hz}\)

and \(v_2=\frac{\mathrm{v}}{\lambda_2}=\frac{330}{5 \cdot 5}=60 \mathrm{~Hz}\)

Number of beats per second =\(v_1-v_2 \)

= 66 – 60 = 6 .

Question 40. Two vibrating tuning forks produce progressive waves given y₁ = 4 sin 500 πt and y₂ = 2 sin 5067πt. Number of beats produced per minute is:

1. 360
2. 180
3. 60
4. 3

Answer: 4. 3

⇒ \(y_1 =4 \sin 500 \pi t \)

⇒ \(y_2 =2 \sin 506 \pi t\)

⇒ \(\omega_1 =500 \pi, \omega_2=506 \pi\)

⇒ \(v_1 =\frac{\omega_1}{2 \pi}=\frac{500 \pi}{2 \pi}\)=250

⇒ \( v_2 =\frac{\omega_2}{2 \pi}=\frac{506 \pi}{2 \pi}\)=253

v = \(v_2-v_1=253-250\)

= 3beats/s

Question 41. Two strings A and B have lengths I_A and I_B and carry masses M_A and M_B at their lower ends, the upper ends being supported by rigid supports, If, n_A and n_B are the frequencies of their vibrations and n_A = 2 n_B, then:

1. I_A = 4I_B, regardless of masses
2. I_B = 4I_B, regardless of masses
3. M_A = 2 M_B, I_A= 2I_B
4. M_B = 2 M_A, IB = 2I_A

Answer: 2. I_B = 4I_B, regardless of masses

We have, the frequency of vibrations of string, n=\(\frac{1}{2 \pi} \sqrt{\frac{g}{I}}\) →   Equation 1

Given, \(n_A=2 n_B\)

⇒ \(\frac{1}{2 \pi} \sqrt{\frac{g}{I_A}}=2 \cdot \frac{1}{2 \pi} \sqrt{\frac{g}{I_B}}\)

⇒ \(\frac{1}{I_A}=\frac{4}{I_B}\)

⇒ \(I_B=4 I_A\)

It is clear from eq (1), that the frequency of vibrations of string does not depend on their masses.

Question 42. A wave has SHM (simple harmonic motion) whose period is 4s while another wave which also possesses SHM has a period of 3s. If both are combined, then the resultant wave will have a period equal to:

1. 4 s
2. 5 s
3. 12 s
4. 3 s

Answer: 3. 12 s

Beats are produced when both waves are combined. Frequency of beats will be \(v_1-v_2=\frac{1}{T_1}-\frac{1}{T_2}=\frac{1}{3}-\frac{1}{4}=\frac{1}{12}\)

Hence, time period = 12 s

Question 43. Two cars moving in opposite directions approach each other with speeds of 22 m/s and 16.5 m/s respectively. The driver of the first car blows a horn having a frequency of 400 Hz. The frequency heard by the driver of the second car is [velocity of sound 340 m/s]:

1. 350 Hz
2. 361 Hz
3. 411 Hz
4. 448 Hz

Answer: 4. 448 Hz

If \(f_0\)= original frequency of source

⇒ \(\mathrm{v}_s\)= speed of source

⇒ \(v_0\)= speed of observer

⇒ \(\mathbf{v}\)= speed of sound

Then if both source and observer are moving towards each other the apparent frequency is \(f_{\mathrm{A}}=f_0\left(\frac{\mathrm{v}+\mathrm{v}_0}{\mathrm{v}-\mathrm{v}_s}\right)\)

In the given question, f₀=400, frequency of horn \({v}_0\)=16.5, speed as observe in 2 case.

⇒ \(\mathrm{v}_s\)= Speed of car =22 m/s

The frequency heard by the driver in the car \(f_{\mathrm{A}} =f_0\left(\frac{\mathrm{v}+\mathrm{v}_0}{\mathrm{v}-\mathrm{v}_s}\right)\)

= 400\(\left(\frac{340+16.5}{340-22}\right)=\frac{356.5 \times 400}{318}\)

= 448 Hz

Question 44. A siren emitting a sound of frequency 800 Hz moves away from an observer towards a cliff at a speed of 15 ms^-1. Then, the frequency of sound that the observer hears in the echo reflected from the cliff is: (Take velocity of ground in air = 330 ms^-1)

1. 800 Hz
2. 838 Hz
3. 885 Hz
4. 765 Hz

Answer: 2. 838 Hz

The frequency of sound observed hear in the echo reflected from the diff. is given by

⇒ \(n^{\prime}=\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_S} n_0\)

⇒ \({\mathrm{v}=330, \mathrm{v}_s=15, n_o=800 \text { given }}\)

⇒ \(n^{\prime}=\frac{330}{330-15} \times 800 \)

= \(\frac{330 \times 800}{315}=838 \mathrm{~Hz}\)v

Question 45. A source of sound S emitting waves of frequency 100 Hz and an observer O are located at some distance from each other. The source is moving with a speed of 19.4 ms^-1 at an angle of 60° with the source observer line as shown in the figure. The observer is at rest. The apparent frequency observed by the observer (velocity of sound in air 330 ms^-1), is:

1. 100 Hz
2. 103 Hz
3. 106 Hz
4. 97 Hz

Answer: 2. 103 Hz

According to question The apparent frequency heard by observer is \(f_0=f_s\left[\frac{\mathrm{v}}{\mathrm{v}-\mathrm{v}_s \cos 60^{\prime \prime}}\right]\)

Given , \(f_s=100 \mathrm{~Hz}\)

⇒ \(\mathrm{v}=330 \mathrm{~m} / \mathrm{s}\)

⇒ \(\mathrm{v}_s=19.4 \mathrm{~ms}^{-1}\)

⇒ \(f_0=100\left[\frac{330}{330-19.4 \times \frac{1}{2}}\right]\)

= \(100\left[\frac{330}{330-9.7}\right]\)

= \(100\left[\frac{330}{320.3}\right]=103.02 \mathrm{~Hz}\)

Question 46. A speeding motorcyclist sees a traffic jam ahead of him. He shows down to 36 km/h. He finds that traffic has eased and a car moving ahead of him at 18 km/h is honking at a frequency of 1392 Hz. If the speed of sound is 343 m/s, the frequency of the honk as heard by him will be:

1. 1332 Hz
2. 1372 Hz
3. 1412 Hz
4. 1454 Hz

Answer: 3. 1412 Hz

When both observer and source are moving, then the apparent frequency is:

Given: \(\{36 \mathrm{~km} / h=36 \times \frac{5}{18}=10 \mathrm{~ms}^{-1}\).

18 \(\mathrm{~km} / h=18 \times \frac{5}{18}=5 \mathrm{~ms}^{-1}\)

f= \(f_0\left[\frac{\mathrm{v}+\mathrm{v}_0}{\mathrm{v}+\mathrm{v}_{\mathrm{s}}}\right]\left[\text { Since, } f_0=1392 \mathrm{~Hz}\right]\)

= \(1392\left[\frac{343+10}{343+5}\right] \)

= \(1392\left[\frac{353}{348}\right]\)

f= \(1412 \mathrm{~Hz}\)

Question 47. Two sources P and Q produce notes of frequency 660 Hz each. A listener moves from P to Q with a speed of 1 ms^-1. If the speed of sound is 330 m/s, then the number of beats heard by the listener per second will be:

1. 4
2. 8
3. 2
4. zero

Answer: 1. 4

According to the question,

Speed of listener \(\mathrm{v}_L=1 \mathrm{~ms}^{-1}\)

Speed of sound v=330 \mathrm{~ms}^{-1}[/latex]

Frequency of each source v=\(600 \mathrm{~Hz}\)

Apparent frequency due to P=\(\mathrm{v}^{\prime}=\frac{\mathrm{v}\left(\mathrm{v}-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}\)

Apparent frequency due to \(\mathrm{Q}=\mathrm{v}^{\prime \prime}=\frac{\mathrm{v}\left(\mathrm{v}-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}\)

No. of beat heard by the listener per second.

⇒ \(\mathrm{V}^{\prime \prime}-\mathrm{V}^{\prime} =\frac{v\left(\mathrm{v}-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}-\frac{v\left(\mathrm{v}_0-\mathrm{v}_{\mathrm{L}}\right)}{\mathrm{v}}\)

= \(\frac{2 v_{\mathrm{L}}}{v}=\frac{2 \times 660 \times 1}{330}\)=4

Question 48. A train moving at a speed of 200 ms¹ toward a stationary object, emits a sound of frequency 100 Hz. Some of the sound reaching the object gets reflected to the train as an echo. The frequency of the echo as detected by the driver of the train is:(speed of sound in air is 300 ms^-1)

1. 3500 Hz
2. 4000 Hz
3. 5000 Hz
4. 3000 Hz

Answer: 3. 5000 Hz

From Doppler’s shift, we have

⇒ \(n^1 =v\left(\frac{v+v_s}{v-v_s}\right)\)

=\(100(\frac{330+220}{330-220})\)

=\(100 \times \frac{550}{110}=5000 \mathrm{~Hz}\)

Question 49. The driver of a car travelling with speed 30 ms^-1 towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330 ms^-1, the frequency of reflected sound as heard by the driver is:

1. 550 Hz
2. 555.5 Hz
3. 720 Hz
4. 500 Hz

Answer: 3. 720 Hz

Applying Doppler’s effect we have,

⇒ \(n^{\prime \prime} =\frac{v+30}{v-30} n \)

= \(\frac{360}{300} \times 600\)

= \(720 \mathrm{~Hz}\)

Question 50. A car is moving towards a high cliff. The driver sounds a horn of frequency f. The reflected sound heard by the driver has a frequency of 2 f. If v is the velocity of sound, then the velocity of the car, in the same velocity units, will be:

1. \(\frac{v}{\sqrt{2}}\)
2. \(\frac{v}{3}\)
3. \(\frac{v}{4}\)
4. \(\frac{v}{2}\)

Answer: 2. \(\frac{v}{3}\)

According to the given conditions,

Cliff is the stationary source of frequency f, where

⇒ \(f^{\prime}=\left(\frac{\mathrm{v}+\mathrm{v}_{\mathrm{car}}}{\mathrm{v}-\mathrm{v}_s}\right) f^{\prime}\)

Frequency heard by the drives or \(f^{\prime \prime}=\left(\frac{\mathrm{v}+\mathrm{v}_{c a r}}{v-v_{\mathrm{s}}}\right) f l\)

2 f=\(\left(\frac{\mathrm{v}+\mathrm{v}_{c a r}}{v-v_{\mathrm{s}}}\right) f\)

⇒ \(v+v_{\text {car }} =2 v-2 v_{\text {car }}\)

⇒ \(3 v_{\text {car }}\) =v

∴ \(v_{\text {car }} =\frac{v}{3}\left(\text { as } v_{\mathrm{s}}=v\right)\)

Question 51. An observer moves towards a stationary source of sound with a speed of 1/5th of the speed of sound. The wavelength and frequency of the source emitted are X and / respectively. The apparent frequency and wavelength recorded by the observer are respectively:

1. 1.2f, 1.2λ
2. 1.2f,  λ
3. f, 1.2 λ
4. 0.8f, 0.8 λ

Answer: 2. 1.2f, λ

Source is stationary,\(\lambda\)= constants

and f=\(\frac{v+v_{\mathrm{S}}}{v} f=\left(1+\frac{v_{\mathrm{S}}}{v}\right) f\)

= \(\left(1+\frac{1}{5}\right)\) f=1.2 f

Question 52. A whistle revolves in a circle with angular speed, co = 20 rad s^-1 using a string of length 50 cm. If the frequency of sound from the whistle is 385 Hz, then what is the minimum frequency heard by an observer who is away from the centre (vrorn6: 340 ms ¹)?

1. 385 Hz
2. 374Hz
3. 394Hz
4. 333 Hz

Answer: 2. 374Hz

Velocity of source is given as \(v_{\text {source }}=0.5 \times 20=10 \mathrm{~ms}^{-1}\)

Minimum frequency is \(f_{\min } =\left(\frac{\mathrm{v}}{\mathrm{v}+\mathrm{v}_s}\right) f\)

= \(\frac{340}{340+10} \times 385=374 \mathrm{~Hz}\)

Question 53. A vehicle, with a horn of frequency h, is moving with a velocity of 30 m/s in a direction perpendicular to the straight line joining the observer and the vehicle. The observer perceives the sound to have a frequency n+ n₁ Then (If the sound velocity in air is 300 m/s):

1. n₁ = 10n
2. n₁ = 0
3. n₁ = 0.1n
4. n₁ = -0.1n

Answer: 2. n₁ = 0

There is no Doppler effect of sound when the velocity of the source (vehicle) is perpendicular to the line between the observer and the source because the component of velocity towards or away from the observer is zero. As a result, there is no apparent difference in frequency. Therefore, n₁ = 0.

Question 54. Two strains move towards each other at the same speed. The speed of sound is 340 m/s. If the height of the tone of the whistle of one of them heard on the other changes 9/8 times, then the speed of each train should be:

1. 20 m/s
2. 2 m/s
3. 200 m/s
4. 2000 m/s

Answer: 1.

According to Doppler’s effect, The apparent frequency of sound heard by the listener differs from the actual frequency of sound generated by the source whenever there is relative motion between the source and the listener.

The apparent frequency of sound wave heard by the listener is \(f=\frac{\mathrm{v}-\mathrm{v}_I}{\mathrm{v}-\mathrm{v}_s} \times f\)

where v is the actual frequency of sound emitted by the source, v. is the source’s velocity, and v1 is the listener’s velocity. If v’= (9/8) v and the source and observer are both moving in the same direction at the same speed (say v), the apparent frequency is

⇒ \(f =f \times\left(\frac{v+v_l}{v+v_s}\right)\)

⇒ \(9 f^{\prime} =f \times \frac{340+\mathrm{v}}{340-\mathrm{v}}\)

17 v =\(340 \times 1\)

or v =\(\frac{340}{17}=20 \mathrm{~m} / \mathrm{s}\)

Oscillations

Question 1. The displacement of a particle executing simple harmonic motion is given by, y=\(y=A_0+A \sin \omega t+B \cos \omega t\) Then the amplitude of its oscillation is given by :

1. \(\sqrt{A^2+B^2}\)
2. \(\sqrt{A_0^2+(A+B)^2}\)
3. A+B
4. \(A_0+\sqrt{A^2+B^2}\)

Answer: 1. \(\sqrt{A^2+B^2}\)

Here: y=\(\mathrm{A}_{\mathrm{o}}+A \sin \omega t+B \cos \omega t\)

Equating with SHM ,\( y^{\prime} =y-\mathrm{A}_{\mathrm{o}}=\mathrm{A} \cos \left(\frac{\pi}{2}-\omega t\right)+\mathrm{B} \cos \omega \mathrm{t}\)

=A \(\sin \omega t+B \cos \omega \mathrm{t}\) .

Resultant amplitude, R =\(\sqrt{A^2+B^2+2 A B \cos 90^{\circ}}\)

=\(\sqrt{A^2+B^2}\)

Question 2. The distance covered by a particle undergoing SHM in one time period is (amplitude = A):

1. zero
2. A
3. 2A
4. 4A

Answer: 4. 4A

In an SHM particle moves from the mean position to an extreme position (P) and then returns to the mean position covering the same distance A.

A + A + A + A = 4 A

Question 3. When two displacement represented by \(y_1=a \sin (\omega t)\) and \(y_2=b \cos (\omega t)\) are superimposed, the motion is:

1. not a simple harmonic
2. simple harmonic with amplitude
3. simple harmonic with amplitude \(\sqrt{a^2+b^2}\)
4. simple harmonic with amplitude \(\frac{(a+b)}{2}\)

Answer: 3. simple harmonic with amplitude \(\sqrt{a^2+b^2}\)

From the question, \(y_1 =a \sin \omega t\)

⇒ \(y_2=b \cos \omega t \)

=b \(\sin \left(\omega t+\frac{\pi}{2}\right)\)

Read and Learn More NEET Physics MCQs

Resultant displacement is y=\(y_1+y_2\)=a \(\sin \omega t+b \sin \left(\omega t+\frac{\pi}{2}\right)\)

{Since \(\sin (A+B)\)=\(\sin A \cos B+\cos A \sin B\}\)

y=a \(\sin \omega t+b \sin (\omega t) \cos \frac{\pi}{2}+b \cos (\omega t) \sin \left(\frac{\pi}{2}\right)\)

y= \(a \sin (\omega t)+b \cos (\omega t)\)

Again Let b \(\cos (\omega t)=\mathrm{A} \cos \theta\) →  Equation 1

and a \(\sin (\omega t)=\mathrm{A} \sin \theta\)  → Equation 2

Squaring and Adding eq. (1) and (2)

A = \(\sqrt{a^2+b^2}\)

y = \(\sqrt{a^2+b^2} \sin (\omega t+\theta)\)

∴ \(\sqrt{a^2+b^2}\) is the amplitude of SHM

Question 4. Out of the following functions representing motion of a particle which represents SHM:

1. y=\(\sin \omega t-\cos \omega t\)
2. y=\(\sin ^3 \omega t\)
3. y=\(5 \cos \left(\frac{3 \pi}{4}-3 \omega t\right)\)
4. y=\(1+\omega t+\omega^2 t^2\)

1. Only (4) does not represent SHM
2. (1) and (3)
3. (1) and (2)
4. Only (1)

Answer: 3. (1) and (2)

For a S.H.M. \(\mathrm{a} \alpha \frac{d^2 y}{d t^2} \alpha-y\)

Hence equation y=\(\sin \omega t-\cos \omega t\) and

y= \(5 \cos \left(\frac{3 \pi}{4}-3 \omega t\right)\) are satisfying this condition.

Question 5. Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie in a straight line perpendicular to the paths of the two particles. The phase difference is:

1. zero
2. \(\frac{2 \pi}{3}\)
3. \(\pi\)
4. \(\frac{\pi}{6}\)

Answer: 2. \(\frac{2 \pi}{3}\)

The Equation becomes, \(y_1 =\frac{A}{2}=A \sin \omega t \)

⇒ \(\omega t =30^{\circ}\)

⇒ \(y_2 =\frac{A}{2}=A \sin \left(\omega t+\frac{\pi}{2}\right)\)

= \(\omega t+\frac{\pi}{2}=150^{\circ}\)

phase difference \(\Delta \phi =\phi_2-\phi_1 \)

= \(150-30=120^{\circ}\)

= \(\frac{2 \pi}{3} \mathrm{rad}\)

Question 6. The displacement of a particle along the x-axis is given by x = \(x=\mathrm{a} \sin ^2 \omega t\). The motion of the particle corresponds to:

1. simple harmonic motion of frequency \(\omega / \pi\)
2. simple harmonic motion of frequency\(3 \omega / 2 \pi\)
3. nonsimple harmonic motion
4. simple harmonic motion of frequency \(\pi\omega / 2 \)

Answer: 3. nonsimple harmonic motion

According to the question, x=a \(\sin ^2 \omega t\) →  Equation 1

Differentiating eq. (1) w.r.t. t we get

⇒ \(\frac{d x}{d t}=2 a \omega(\sin \omega t)(\cos \omega t)\)

Again differentiating w.r.t. t we have

a=\(\frac{d^2 x}{d t^2} =2 a \omega^2\left[\cos ^2 \omega t-\sin ^2 \omega t\right]\)

=2 a \(\omega^2 \cos 2 \omega t\)  → Equation 2

The eq. (2) does not satisfy the condition of SHM’ So, motion is not simPle harmonic’

Question 7. A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is

1. \(\frac{T}{8}\)
2. \(\frac{T}{12}\)
3. \(\frac{T}{2}\)
4. \(\frac{T}{4}\)

Answer: 2. \(\frac{T}{12}\)

For equilibrium position, x(t)=a \(\sin \omega t\)

At, x(t)=\(\frac{a}{2}\)

⇒ \(\sin(\frac{\pi}{6})=\sin \omega t {\omega=\frac{2 \pi}{\mathrm{T}}}\)

or \(\frac{\pi}{6}=\frac{2 \pi t}{T}\)

t=\(\frac{T}{12}\)

Question 8. The circular motion of a particle with constant speed is:

1. periodic but not simple harmonic
2. simple harmonic but not periodic
3. period and simple harmonic
4. neither periodic nor simple harmonic

Answer: 1. periodic but not simple harmonic

A particle is a constant-speed circular motion that repeats its motion at regular intervals but does not oscillate around a fixed location. As a result, particle motion is periodic but not simply harmonic’

Question 9. Two simple harmonic motions with the same frequency act on a particle at right angles i.e. along X-axis and 7-axis. If the two amplitudes are equal and the phase difference is \(\frac{\pi}{2}\) the resultant motion will be:

1. a circle.
2. an ellipse with the major axis along the Y-axis.
3. an ellipse with the major axis along the X-axis.
4. a straight line inclined at 45° to the X-axis.

Answer: 1. a circle

The equations of two simple harmonic motions can be written as x=\(a \sin \omega t \) Equation 1

and y=\(a \sin \left(\omega t+\frac{\pi}{2}\right)\)

y=\(a \cos \omega t\) Equation 2

On squaring and adding Eqs. (1) and (2), we get

⇒ \(x^2+y^2 =a^2\left(\sin ^2 \omega t+\cos ^2 \omega t\right)\)

or \(x^2+y^2 =a^2\)

It represents the equation of a circular motion with radius a.

Question 10. A Simple harmonic oscillator has an amplitude of a and a period of T. The time required by it to travel from,\(x=a \text { to } x=\frac{a}{2}\) is:

1. \(\frac{T}{6}\)
2. \(\frac{T}{4}\)
3. \(\frac{T}{3}\)
4. \(\frac{T}{2}\)

Answer: 1. \(\frac{T}{6}\)

We have, the equation of simple harmonic motion given by,

or x =\(a \sin \omega t\)

= \(a \sin \left(\frac{2 \pi}{T}\right) t\)

when, x =a , then

a = \(a \sin \left(\frac{2 \pi}{T}\right) t \)

⇒ \(\sin \left(\frac{2 \pi}{T}\right) t\) =1

⇒ \(\sin \left(\frac{2 \pi}{T}\right) t =\sin \frac{\pi}{2}\)

t =\(\frac{T}{4}\)

when x=\(\frac{a}{2}\), then

⇒ \(\frac{a}{2} =a \sin \left(\frac{2 \pi}{T} \cdot t\right)\)

⇒ \(\sin \left(\frac{2 \pi}{T} t\right) =\sin \frac{\pi}{6}\)

t=\(\frac{T}{12}\)

Hence, the time taken to travel from

x=a to x=\(\frac{a}{2}=\frac{T}{4}-\frac{T}{12}=\frac{T}{6}\)

Question 11. The composition of two simple harmonic motions of equal periods at a right angle to each other and with a phase difference of \(\pi\) results in the displacement of the particles along:

1. circle
2. figure of eight
3. straight line
4. ellipse

Answer: 3. straight line

For simple harmonic motion,

x =\(a \sin \omega \mathrm{t}\)  →  Equation 1

and y =\(b \sin (\omega \mathrm{t}+\pi)\)

y =\(-b \sin \omega \mathrm{t}\)  →  Equation 2

or From eq. (1) and (2), we get

⇒ \(\frac{x}{a} =\sin \omega \mathrm{t} \)

and \(-\frac{y}{b} =\sin \omega \mathrm{t}\)

⇒ \(\frac{x}{a} =-\frac{y}{b}\)

y =\(-\frac{b}{a} x\)

Hence, it is an equation of a straight line

Question 12. The radius of the circle, the period of revolution, the initial position, and the sense of revolution are indicated in the below figure. y-projection of the radius vector of rotating particle P is :

1. y(t)=\(4 \sin \left(\frac{\pi t}{2}\right)\), where y in m
2. y(t)=\(3 \cos \left(\frac{3 \pi t}{2}\right)\), where y in m
3. y(t)=\(3 \cos \left(\frac{\pi t}{2}\right)\), where y in m
4. y(t)=\(-3 \cos 2 \pi t\), where y in m

Answer: 3. y(t)=\(3 \cos \left(\frac{\pi t}{2}\right)\), where y in m

Here, T=4 s, A=3 m

Time Period, \(\mathrm{T}=\frac{2 \pi}{\omega}\)

⇒ \(\omega =\frac{2 \pi}{T}=\frac{2 \pi}{4}=\frac{\pi}{2} \mathrm{rad} / \mathrm{s}\)

y =a cost \(\omega t=3 \cos \frac{\pi}{2} t\)

Question 13. A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of the velocity is equal to that of its acceleration. Then, its period in seconds is

1. \(\frac{\sqrt{5}}{\pi}\)
2. \(\frac{\sqrt{5}}{2 \pi}\)
3. \(\frac{4 \pi}{\sqrt{5}}\)
4. \(\frac{2 \pi}{3}\)

Answer: 3. \(\frac{4 \pi}{\sqrt{5}}\)

Given the magnitude of the velocity of a particle = magnitude of the acceleration of a particle in SHM  →  Equation 1

The magnitude of the velocity of grice at a displacement from the mean position is, \(\omega \sqrt{A^2-y^2}\), and the magnitude of the acceleration of particles in SHM is \(\omega^2 y\)

Then eq. (1) becomes,

⇒ \(\omega \sqrt{A^2-y^2} =\omega^2 y \)

⇒ \(\omega =\frac{\sqrt{A^2-y^2}}{y}=\frac{\sqrt{(3)^2-(2)^2}}{2}\)

= \(\frac{\sqrt{9-4}}{2}=\frac{\sqrt{5}}{2}\)

Time period, T=\(\frac{2 \pi}{\omega}=\frac{2 \pi}{\sqrt{5} / 2}=\frac{4 \pi}{\sqrt{5}}\)

Time period, T=\(\frac{4 \pi}{\sqrt{5}} s\)

Question 14. Two simple harmonic motions given by, \(x=a \sin \omega \mathrm{t}+\lambda \text { and } y=a \sin \left(\omega t+\delta+\frac{\pi}{2}\right)\)act on a particle simultaneously, then the motion of particle will be

1. circular anti-clockwise
2. circular clockwise
3. elliptical anti-clockwise
4. elliptical clockwise

Answer: 2. circular clockwise

x= a \(\sin (\omega t+\delta)\)

y= \(a \sin \left(\omega t+\delta+\frac{\pi}{2}\right)\)

or y= a \(\cos (\omega t+\delta)\)

Squaring and adding eq. (i) and (ii), we get

⇒ \(x^2+y^2=a^2\left[\sin ^2(\omega t+\delta)+\cos ^2(\omega t+\delta)\right]\)

or \(x^2+y^2=a^2\left(\sin ^2 \theta+\cos ^2 \theta=1\right)\)

This represents a circle.

At \((\omega t+\delta)\)=0 ; x=0, y=a

At \((\omega t+\delta)=\frac{\pi}{2}\) ; x=a, y=0

At \((\omega t+\delta)=\pi\) ; x=0, y=-a

At\( (\omega t+\delta)=\frac{3 \pi}{2}\) ; x=-a, y=0

At \((\omega t+\delta)=2 \pi\) ; x=0, y=a

It is clear That the particle motion is in a circular clockwise direction.

Question 15. The phase difference between displacement and acceleration of a particle in a simple harmonic motion is :

1. \(\frac{3 \pi}{2} \mathrm{rad}\)
2. \(\frac{\pi}{2} \mathrm{rad}\)
3. zero
4. \(\pi \mathrm{rad}\)

Answer: 4. \(\pi \mathrm{rad}\)

In Simple Harmonic Motion, The equation of displacement of the particle is y=\(a \sin \omega t\) → Equation 1

And the equation of acceleration of the particle is, a \(\omega^2 \sin \omega t=a \omega^2 \sin (\omega t+\pi)\)  → Equation 2

From eq. (1) and equation (2)

The phase difference between displacement and acceleration of the particle is :

⇒ \(\phi=(\omega t+\pi)-\omega t\)

⇒ \(\phi=\omega t+\pi-\omega t=\pi \text { radian }=\pi \mathrm{rad}\) .

Question 16. The average velocity of a particle executing SHM complete vibration is :

1. \(A \omega\)
2. \(\frac{A \omega^2}{2}\)
3. zero
4. \(\frac{A \omega}{2}\)

Answer: 3. zero

In one complete vibration, displacement is \(2 \pi \omega\). So, the average velocity in one complete vibration is :

∴ \(\frac{\text { Displacement }}{\text { Time Interval }}=\frac{y_1-y_2}{\mathrm{~T}}\)=0

Question 17. The particle is executing SHM along a straight line. Its velocities at distance x₁ and x₂ from the mean position or v₁ and v₂ respectively. Its period is:

1. \(2 \pi \sqrt{\frac{x_1^2+x_2^2}{v_1^2+v_2^2}}\)
2. \(2 \pi \sqrt{\frac{x_1^2-x_2^2}{v_1^2-v_2^2}}\)
3. \(2 \pi \sqrt{\frac{v_1^2+v_2^2}{x_1^2+x_2^2}}\)
4. \(2 \pi \sqrt{\frac{v_1^2-v_2^2}{x_1^2-x_2^2}}\)

Answer: 2. \(2 \pi \sqrt{\frac{x_1^2-x_2^2}{v_1^2-v_2^2}}\)

We know under SHM if A is the amplitude of  oscillation, then the velocity

⇒ \(v_1^2=\omega^2\left(\mathrm{~A}^2-x_1^2\right)\)

⇒ \(v_2^2=\omega^2\left(\mathrm{~A}^2-x_2^2\right)\)

Where \(x_1\) and \(x_2\) are the displacement of particles from the mean position,

Subtracting eq. (2) from eq (1) we have,

⇒ \(v_2^2-v_1^2 =\omega^2\left(x_2^2-x_1^2\right)\)

⇒ \(\omega =\sqrt{\frac{v_2^2-v_1^2}{x_2^2-x_1^2}}\)

⇒ \(\frac{2 \pi}{T}=\sqrt{\frac{v_2^2-v_1^2}{x_2^2-x_1^2}}\)

T =\(2 \pi \sqrt{\frac{x_2^2-x_1^2}{v_2^2-v_1^2}}\)

Question 18. A particle is executing a simple harmonic motion. Its maximum acceleration is \(\alpha\) and its maximum velocity is \(\beta\). Then, its period of vibration will be:

1. \(\frac{\beta^2}{\alpha^2}\)
2. \(\frac{\alpha}{\beta}\)
3. \(\frac{\beta^2}{\alpha}\)
4. \(\frac{2 \pi \beta}{\alpha}\)

Answer: 4. \(\frac{2 \pi \beta}{\alpha}\)

Acceleration of particles does.ng SHM is,

⇒ \(\alpha=A \omega^2\)  → Equation 1

A= maximum amplitude

⇒ \(\omega\)= angular velocity of particle

Again Maximum velocity,

⇒ \(\beta=A \omega\)  → Equation 2

From eq. (1) and (2) we have

⇒ \(\frac{\alpha}{\beta}=\frac{A \omega^2}{A \omega}=\omega=\frac{2 \pi}{T}\)

T=\(\frac{2 \pi \beta}{\alpha}\)

Time period of vibration, T=\(\frac{2 \pi \beta}{\alpha}\)

Question 19. The oscillation of a body on a smooth horizontal surface is represented by the equation, x = \(x=A \cos (\omega t)\)

1. where, x = displacement at time t
2. \(\omega\) = frequency of oscillation
3. Which one of the following graphs shows correctly the variation a with t?
4. Here, a = acceleration at time t,T= time period

Answer: 1. where, x = displacement at time t

The oscillation of the body on a smooth horizontal surface u.

X= \(A \cos \omega t\)

Where, X= displacement at t

⇒ \(\omega\)= frequency of oscillation

A=Amplitude

Here at t=0, X=A

at t=\(\frac{T}{4}, X=A \cos \left(\frac{2 \pi}{T} \times \frac{T}{4}\right)=A \cos \frac{\pi}{2}\)=0

at \(t=\frac{T}{2}, X=A \cos \left(\frac{2 \pi}{T} \times \frac{T}{2}\right)=\mathrm{A} \cos \pi=-\mathrm{A}\)

Question 20. A particle of mass m oscillates along the x-axis according to equation x = a sin \(\omega\). The nature of the graph between the momentum and displacement of the particle is:

1. Circle
2. Hyperbola
3. Ellipse
4. A straight line passing through the origin

Answer: 3. Ellipse

According to the question, x =\(\mathrm{a} \sin \omega t\)

⇒ \(\frac{x}{a} =\sin \omega t\)  → Equation 1

Now velocity v=\(\frac{d x}{d t}=a \omega \cos \omega t\)

⇒ \(\frac{v}{a \omega}=\cos \omega t\)  →  Equation 2

From eq. (1) and (2)

⇒ \(\frac{x^2}{a^2}+\frac{v^2}{a^2 \omega^2}=\sin ^2 \omega t+\cos ^2 \omega t\)

⇒ \(\frac{x^2}{a^2}+\frac{v^2}{a^2 \omega^2}\)=1

∴ This is the equation of an ellipse. So the graph between the moment and displacement of the particle is ellipse.

Question 21. A simple pendulum performs simple harmonic motion x = 0 with an amplitude a and period T. The speed of the pendulum at x =\(\frac{a}{2}\) will be:

1. \(\frac{\pi a \sqrt{3}}{2 T}\)
2. \(\frac{\pi a}{T}\)
3. \(\frac{3 \pi^2 a}{T}\)
4. \(\frac{\pi a \sqrt{3}}{T}\)

Answer: 4. \(\frac{\pi a \sqrt{3}}{T}\)

We know that, V =\(\frac{d y}{d t}=A \omega \cos \omega t\)

= \(A \omega \sqrt{1-\sin ^2 \omega t}\)

= \(A \omega \sqrt{A^2-y^2}\)

Here, y =\(\frac{a}{2}\)

V = \(\omega \sqrt{a^2-\frac{a^2}{4}}=\omega \sqrt{\frac{3 a^2}{4}}\)

= \(\frac{2 \pi}{T} \frac{a \sqrt{3}}{2}=\frac{\pi a \sqrt{3}}{T}\)

Question 22. Which of the following equations of motion represents simple harmonic motion?

1. Acceleration = \(-k_0 x+k_1 x^2\)
2. Acceleration = – k(x + a)
3. Acceleration = k(x + a)
4. Acceleration = kx

Answer: 2. Acceleration = – k(x + a)

Here acceleration a(\(\alpha\)-displacement)

A \(\propto-y\)

A = \(-\omega^2 y \)

A = \(-\frac{k}{m} y\)

A =-k y

And y =x+a

acceleration =-k(x+a)

Question 23. Two simple harmonic motions of angular frequency 100 and 1000 rad \(\mathrm{s}^{-1}\) have the same displacement amplitude. The ratio of their maximum acceleration is:

1. 1: 10
2. 1: 10²
3. 1: 10³
4. 1: 10⁴

Answer: 2. 1: 10²

Acceleration of SHM is, \(a_{\max } =-\omega^2 A\)

or \(\frac{\left(a_{\max }\right)_1}{\left(a_{\max }\right)_2} =\frac{\omega_1^2}{\omega_2^2}\)(A remains same )

or \(\frac{\left(a_{\max }\right)_1}{\left(a_{\max }\right)_2} =\frac{(100)^2}{(1000)^2}=\left(\frac{1}{10}\right)^2 \)

= \(1: 10^2\)

Question 24. A point performs simple harmonic oscillation of period T and the equation of motion is given by x = \(x=a \sin (\omega t+\pi / 6)\). After the elapse of what fraction of the period the velocity of the point will be equal to half of its maximum velocity?

1. \(\frac{T}{8}\)
2. \(\frac{T}{6}\)
3. \(frac{T}{3}\)
4. \(\frac{T}{12}\)

Answer: 4. \(\frac{T}{12}\)

The equation is, x=\(a \sin \left(\omega t+\frac{\pi}{6}\right)\)  → Equation 1

Differentiating we get, v=\(\frac{d x}{d t}=a \omega \cos \left(\omega t+\frac{\pi}{6}\right)\) (Now v=\(\frac{a \omega}{2})\)

⇒ \(\frac{a \omega}{2}=a \omega \cos \left(\omega t+\frac{\pi}{6}\right)\)

⇒ \(\frac{1}{2}=\cos \left(\omega t+\frac{\pi}{6}\right)\)

⇒ \(\cos \frac{\pi}{3} =\cos \left(\omega t+\frac{\pi}{6}\right)\)

⇒ \(\omega t+\frac{\pi}{6} =\frac{\pi}{3}\)

or \(\omega t =\frac{\pi}{6}\)

t =\(\frac{\pi}{6 \omega}=\frac{\pi \times T}{6 \times 2 \pi}=\frac{T}{12}\)

Thus at\( \frac{T}{12}\) velocity of the point will be equal to half of its maximum velocity.

Question 25. The phase difference between the instantaneous velocity and acceleration of a particle executing simple harmonic motion is :

1. \(\pi\)
2. \(0.70 \pi\)
3. zero
4. \(0.5 \pi\)

Answer: 4. \(0.5 \pi\)

Let y=\(A \sin \omega t=A \omega^2 \sin (\omega t+\pi)\)

⇒ \(\frac{d y}{d t} =A \omega \cos \omega t\)

= \(A \omega \sin \left(\omega t+\frac{\pi}{2}\right)\)

Acceleration,\(\frac{d^2 y}{d x^2}=-A \omega^2 \cos \omega t=A \omega^2 \sin (\omega t+\pi)\)

Phase difference =\(\pi-\frac{\pi}{2}\)

Question 26. A particle executing simple harmonic motion of amplitude 5 cm has a maximum speed of 31.4 cm/s. The frequency of its oscillation is:

1. 4 Hz
2. 3 Hz
3. 2 Hz
4. 1 Hz

Answer: 4. 1 Hz

Here a=5 \(\mathrm{~cm}, V_{\max }=\frac{31.4 \mathrm{~cm}}{\mathrm{~s}}\)

⇒ \(V_{\max }=\omega a=31.4=2 \pi \mathrm{v} \times 5\)

31.4=10 \(\times 3.14 \times v \)

v=1 \(\mathrm{~Hz}\)

Question 27. Which one of the following statements is true for the speed v and the acceleration a of a particle executing simple harmonic motion?

1. When v is maximum, a is maximum
2. The value of a is zero, whatever may be the value of v
3. When v is zero, a is zero
4. When v is maximum a is zero

Answer: 4. When v is maximum a is zero

In SHM, Velocity = \(A \omega \sin \left(\omega t+\frac{\pi}{2}\right)\)

Acceleration=A \(\omega^2 \sin (\omega t+\pi)\)

This shows that v is max then a is zero.

Question 28. A particle starts a simple harmonic motion from the mean position. Its amplitude is a and its period is T. What is its displacement when its speed is half of its maximum speed?

1. \(\frac{\sqrt{2}}{3} a\)
2. \(\frac{\sqrt{3}}{2} a\)
3. \(\frac{2}{\sqrt{3}} a\)
4. \(\frac{a}{\sqrt{2}} a\)

Answer: 2. \(\frac{\sqrt{3}}{2} a\)

At any given time, the velocity of the particle executing SHM is defined as the rate of change of its displacement.

Let the displacement of the particle at an instant be given by

Velocity, v = \(\frac{d x}{d t}=\frac{d(a \sin \omega t)}{d t}\)

=\(a \omega t \cos \omega t\)

= \(a \omega \sqrt{\left(1-\sin ^2 \omega t\right)}\)

= \(a \omega \sqrt{\left(1-\frac{x^2}{a^2}\right)}=w \sqrt{\left(a^2-x^2\right)}\)

At mean position, x=0

⇒ \(v_{\max }=\omega a\)

According to question, v=\(\frac{\mathrm{v}_{\max }}{2}=\frac{\mathrm{a} \omega}{2}\)

But, v=\(\omega \sqrt{a^2-x^2}\)

= \(\frac{a \omega}{2}=\omega \sqrt{a^2-x^2}\)

Or x=\(\frac{\sqrt{3}}{2} a\)

Question 29. A body executes SHM with an amplitude a. At what displacement from the mean position, the potential energy of the body is one-fourth of its total energy?

1. \(\frac{\mathrm{a}}{4}\)
2. \(\frac{a}{2}\)
3. \(\frac{3 a}{4}\)
4. Some other fraction of a

Answer: 2. \(\frac{a}{2}\)

We have, the potential energy of a body executing SHM, U=\(\frac{1}{2} m \omega^2 x^2\)

The total energy of the body executing SHM,

E=\(\frac{1}{2} m \omega^2 a^2\)

According to the question, U =\(\frac{1}{4} E \)

⇒ \(\frac{1}{2} m \omega^2 x^2 =\frac{1}{4} \times \frac{1}{2} m \omega^2 a^2 \)

⇒ \(x^2 =\frac{a^2}{4}\)

x =\(\frac{a}{2}\)

Question 30. A particle moving along the X-axis executes simple harmonic motion, and then the force acting on it is given by where A and K are positive constants.

1. – AKx
2. Acos Kx
3. Aexp(-Ax)
4. AKx

Answer: 1. – AKx

If a particle in simple harmonic motion moves x distant from its equilibrium position, the magnitude of the restoring force 17acting on the particle at that instant is given by F =-kx

where k is known as the force constant. Hence, in given options, option (A) is correct. Here, k = Ak.

Question 31. A body is executing simple harmonic motion with frequency V, the frequency of its potential energy is:

1. n
2. 2n
3. 3n
4. 4n

Answer: 1. n

Given, SHM frequency = n

PE frequency =?

Since PE frequency is the same as SHM frequency.

Question 32. A particle of mass m is released from rest and follows a parabolic path as shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time:

Answer: 4.

Motion starts from an extreme position and for small displacement it is SHM.

∴ \(y=\mathrm{A} \cos (\omega t+\phi)\)

Question 33. The particle executing simple harmonic motion has a kinetic energy \(K_0 \cos ^2 \omega t\)t. The maximum values of the potential energy and the total energy are respectively:

1. \(K_0 / 2\) and \( K_0\)
2. \(K_0 \)and \( 2 K_0\)
3. \(K_0 \)and \( K_0\)
4. \(0\) and \( 2 K_0\)

Answer: 3. \(K_0\) and \( K_0\)

⇒ \(K. E. =K_0 \cos ^2 \omega t\)

Maximum P. E. Maximum K. E. Total energy

= \(K_0\)

Question 34. A particle of mass m oscillates with simple harmonic motion between points X₁ and X₂, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph:

Answer: 1.

PE in SHM =\(\frac{1}{2} K x^2\) →  equation of parabola

Question 35. The potential energy of a simple harmonic oscillator when the particle is halfway to its endpoint is:

1. \(\frac{2}{3} E\)
2. \(\frac{1}{8} E\)
3. \(\frac{1}{4} E\)
4. \(\frac{1}{2} E\)

Answer: 3. \(\frac{1}{4} E\)

P.E. =\(\frac{1}{2} K x^2 \)

=\(\frac{1}{2} K\left(\frac{x}{2}\right)^2=\frac{E}{4}\)

Question 36. The displacement between the maximum potential energy (P.E.) position and the maximum energy (K.E.) position for a particle executing simple harmonic motion is:

1. \(\pm \frac{a}{2}\)
2. \(\pm \mathrm{a}\)
3. \(\pm 2 \mathrm{a}\)
4. \(\pm 1\)

Answer: 2. \(\pm \mathrm{a}\)

The K.E. of pendulum, K.E.=\(\frac{1}{2} K\left(a^2-y^2\right)\)

and P.E. of pendulum =\(\frac{1}{2} K Y^2\)

when y = 0 (mean position) K.E. is maximum and PE is 0

When: 0, K.E. is 0 and P.E. is maximum.

The displacement between the position of maximum potential energy and maximum kinetic energy is \(\pm\) a

Question 37. In SHM restoring force is F = – kx, where k is force constant, x is displacement and a is amplitude of motion, then total energy depends upon:

1. k, a and m
2. k, x, m
3. k, a
4. k, x

Answer: 3. k, a

In simple harmonic motion, the total energy = Potential energy + Kinetic energy

or E = U + K

= \(\frac{1}{2} m \omega^2 x^2+\frac{1}{2} m \omega^2\left(a^2-x^2\right)\)

= \(\frac{1}{2} m \omega^2 a^2+\frac{1}{2} k a^2 \)

Where, k = force constant = \(m \omega^2\)

Question 38. In a simple harmonic motion, when the displacement is one-half the amplitude, what fraction of the total energy is kinetic?

1. Zero
2. \(\frac{1}{4}\)
3. \(\frac{1}{2}\)
4. \(\frac{3}{4}\)

Answer: 4. \(\frac{3}{4}\)

The total energy of a particle executing SHM at instant time t,

E=\(\frac{1}{2} m^2 \omega a^2\)  → Equation 1

and kinetic energy of the particle at instant t,

⇒ \(E_K=\frac{1}{2} m \omega^2\left(a^2-x^2\right)\)  → Equation 2

when x =\(\frac{a}{2}\),

⇒  \(E_K =\frac{1}{2} m \omega^2\left(a^2-\frac{a^2}{4}\right)\)

=\(\frac{1}{2} m \omega^2 \times \frac{3}{4} a^2 \)

⇒ \(E_K =\frac{1}{2} \times \frac{3}{4} m \omega^2 a^2\) →  Equation 3

Or From Eqs. (1) and (3), we get

⇒  \(\frac{E_K}{E} =\frac{3}{4}\)

∴ \(E_K \frac{3}{4} E\)

Question 39. The angular velocity and the amplitude of a simple pendulum are co and a respectively. At a displacement x from the mean position, if its kinetic energy is T and potential energy is U, then the ratio of T to U is

1. \(\left(\frac{a^2-x^2 \omega^2}{x^2 \omega^2}\right)\)
2. \(\frac{x^2 \omega^2}{\left(a^2-x^2 \omega^2\right)}\)
3. \(\frac{\left(a^2-x^2\right)}{x^2}\)
4. \(\frac{x^2}{\left(a^2-x^2\right)}\)

Answer: 3. \(\frac{\left(a^2-x^2\right)}{x^2}\)

Let us consider a particle of mass m that performs linear SHM with an amplitude of, a and a constant angular frequency. Let us assume that the particle’s displacement is x, which is determined by r seconds after starting from the mean position.

We have, x=\(a \sin \omega t\)

So, the potential energy of the particle is, \(\mathrm{U}=\frac{1}{2} m \omega^2 x^2\) → Equation 1

and kinetic energy of particle is, T=\(\frac{1}{2} m \omega^2\left(a^2-x^2\right)\) →  Equation 2

From Eqs. (1) and (2), we get,

⇒  \(\frac{T}{U}=\frac{a^2-x^2}{x^2}\)

Question 40. A particle, with restoring force proportional to displace¬ment and resisting force proportional to velocity is subjected to a force F \(\sin \omega t\). If the amplitude of the particle is maximum for \(\omega=\omega_1\), and the energy of the particle is maximum for \(\omega=\omega_2\), then

1. \(\omega_1=\omega_0 and \omega_2 \neq \omega_0\)
2. \(\omega_1=\omega_0 and \omega_2=\omega_0\)
3. \(\omega_1 \neq \omega_0 and \omega_2=\omega_0 \)
4. \(\omega_1 \neq \omega_0 and \omega_2 \neq \omega_0\)

Answer: 3. \(\omega_1 \neq \omega_0 and \omega_2=\omega_0 \)

As we know the energy of the particle is maximum at natural frequency. Since the restoring force is proportional to the displacement and the resisting force is proportional to velocity.

So, \(\omega_1 \neq \omega_0 \)

And, \(\omega_2 =\omega_0\)

Question 41. Two pendulums of length 121 cm and 100 cm start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is:

1. 11
2. 9
3. 10
4. 8

Answer: 1. 11

Let us consider,L=121 \(\mathrm{~cm}=1.21 \mathrm{~m} ; L^1=100 \mathrm{~cm}=1 \mathrm{~m}\)

T= longer pendulum; \(\mathrm{T}^1\)= shorter pendulum we know,

T=\(2 \pi \sqrt{\frac{l}{g}} \Rightarrow \mathrm{T} \propto \sqrt{l}\)

⇒  \(\frac{T}{T^1} \propto \sqrt{\frac{L}{L^1}}\)

⇒  \(\frac{T}{T^1} \propto \sqrt{\frac{1.21}{1}}=\frac{1.1}{1}\)

10 \(\mathrm{~T}=11 \mathrm{~T}^1\)

So, 10 vibrations of the longer pendulum: 1L vibration of a shorter pendulum

Question 42. A spring is stretched by 5 cm by a force of 10N. The period of the oscillations when a mass of 2 kg is suspended by it is:

1. 0.0628 s
2. 6.28 s
3. 3.14 s
4. 0.628 s

Answer: 4. 0.628 s

Given, Stretch(x)=5cm

Force (F) = 10 N

Mass (m) = 2ke

Time period, T =?

We know, that, the force constant of spring, \(\mathrm{K}=\frac{F}{x}\)

⇒  \(\mathrm{K} =\frac{10}{0.05}=200 \mathrm{~N} / \mathrm{m}\)

⇒  \(\omega =\frac{2 \pi}{\mathrm{T}}\)

⇒  \(\frac{4 \pi^2}{\mathrm{~T}^2} =\frac{k}{m}\)

⇒  \(\mathrm{~T}^2 =4 \pi^2 \frac{m}{k}\)

= \(-2 \pi \sqrt{\frac{m}{\mathrm{~K}}}\)

⇒  \(\mathrm{T}^2 =4 \pi^2 \frac{m}{k}\)

= \(-2 \pi \sqrt{\frac{m}{\mathrm{~K}}}\)

⇒  \(\mathrm{~T} =2 \pi \sqrt{\frac{2}{200}}\)

=\(2 \pi \sqrt{\frac{1}{100}}\)

=\(\frac{2 \pi}{10}\)

∴ \(\mathrm{~T} =\frac{6.28}{10}=0.628 \mathrm{~s}\)

Question 43. A pendulum is hung from the roof of a sufficiently high building and is moving freely from end to end like a simple harmonic oscillator. The acceleration of the bob of the pendulum is 20 m/s² at a distance of 5 m from the mean position. The period of oscillation is:

1. 2s
2. \(\pi s\)
3. 2 \(\pi s\)
4. 1 \(\mathrm{~s}\)

Answer: 2. \(\pi s\)

Acceleration of particle executing SHM at position is given as

⇒  \(|a| =\omega^2 y \) →  Equation 1

Here a = \(20 \mathrm{~ms}^{-1}\)

yy =\(5 \mathrm{~m}\)

20 =\(\omega^2(5)\)

⇒  \(\omega^2\) =4

⇒ \(\omega =2 \mathrm{rad} / \mathrm{s}\)

Time period, T =\(\frac{2 \pi}{\omega}=\frac{2 \pi}{2}=\pi \mathrm{s}\)

T =\(\pi s\)

Question 44. A spring of force constant k is cut into lengths of ratio 1: 2 : 3. They are connected in series and the new force constant is k. If they are connected in parallel and the force constant is k”, then K’: k” is:

1. 1: 6
2. 1: 9
3. 1: 11
4. 1: 14

Answer: 3. 1: 11

Spring constant \(\propto \frac{1}{\text { length }}\)

K=\(\frac{1}{l}\)

i.e. \(K_1=6 K, K_2=3 K and K_3\)=2 K

In series, \(\frac{1}{K^{\prime}}=\frac{1}{6 K}+\frac{1}{3 K}+\frac{1}{2 K}\)

⇒  \(\frac{1}{K^{\prime}}=\frac{6}{6 K}\)

⇒  \(K^{\prime}\)=K

⇒  \(K^{\prime \prime}=6 K+3 K+2 K=11 K\)

⇒ \(\frac{K^{\prime}}{K^{\prime \prime}}=\frac{1}{11}\)

∴ \(K^{\prime}: K^{\prime \prime}\)=1: 11

Question 45. A body of mass m is attached to the lower end of a spring whose end is fixed. The spring has negligible mass When the mass m is slightly pulled down and released, it oscillates with a time period of 3s. When the mass m is increased by 1 kg. The time period of oscillations becomes 5 s. The value of m in kg is:

1. \(\frac{3}{4}\)
2. \(\frac{4}{3}\)
3. \(\frac{16}{9}\)
4. \(\frac{9}{16}\)

Answer: 4. \(\frac{9}{16}\)

According to the question, the diagram is

Time period, T=\(2 \pi \sqrt{\frac{m}{k}}\)

⇒  \(\mathrm{I}^{\text {st }} \text { case, }=T_1=2 \pi \sqrt{\frac{m}{k}}\)  → Equation 1

⇒  \(II ^{\text {nd }}\) case when mass m is increased by 1 \(\mathrm{~kg}\) then mass becomes (m+1)

⇒  \(T_2=2 \pi \sqrt{\frac{m+1}{m}}\) →  Equation 2

from eq. (1) and (2) \(\omega_0\) get

⇒  \(\frac{T_2}{T_1}=\sqrt{\frac{m+1}{m}}\)

⇒  \(\frac{5}{3}=\sqrt{\frac{m+1}{m}}\)

⇒  \(\frac{m+1}{m}=\frac{25}{9} \)

⇒  \(1+\frac{1}{m}=\frac{25}{9}\)

∴ \( m=\frac{9}{16} \mathrm{~kg}\)

Question 46. The period of oscillation of a mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be:

1. T
2. \(\frac{T}{\sqrt{2}}\)
3. 2T
4. \(\sqrt{2} T\)

Answer: 4. \(\sqrt{2} T\)

Time period of simple pendulum T

-T = \(2 \pi \sqrt{\frac{\mathrm{M}}{k}}\)

When mass is double then \(T^{\prime} =2 \pi \sqrt{\frac{2 M}{k}}=\sqrt{2}\left(2 \pi \sqrt{\frac{M}{k}}\right)\)

= \(\sqrt{2} T\)

Question 47. A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion so that the mass gets detached from the pan (take g = 10 m/s²)?

1. 10.0 cm
2. any value less than 12.0 cm
3. 4.0 cm
4. 8.0 cm

Answer: 1. 10.0 cm

For Given Condition, \(m g =m \omega^2 a=k a\)

a =\(\frac{m g}{k}=\frac{2 \times 10}{200}\)

=0.1=10 \(\mathrm{~cm}\)

Question 48. The time period of mass suspended from a spring is T. If the spring is cut into four equal parts and the same mass is suspended from one of the parts, then the new time period will be:

1. \(\frac{T}{4}\)
2. T
3. \(\frac{T}{2}\)
4. 2T

Answer: 3. \(\frac{T}{2}\)

Let K = force constant of spring and

K = force constant of each part then

⇒  \(\frac{1}{K} =\frac{4}{K^{\prime}}\)

⇒  \(K^{\prime}\) =4 K

Time period =\(2 \pi \sqrt{\frac{m}{4 K}}\)

= \(\frac{1}{2} \times 2 \pi \sqrt{\frac{m}{4 K}}=\frac{T}{2}\)

Question 49. The time period of a simple pendulum is 2 s. If its length is increased by 4 times, then its period becomes:

1. 16 s
2. 12 s
3. 8 s
4. 4 s

Answer: 4. 4 s

We have, time period of a simple pendulum

T=2 \(\pi \sqrt{\frac{l}{g}}\)

where, l= length of the pendulum

g= acceleration due to gravity

T \(\propto \sqrt{l}\)

Hence, \(\frac{T_2}{T_1}=\sqrt{\frac{l_2}{l_1}}\)  → Equation 1

Given, \(l_2=4 l_1, T_1=2 \mathrm{~s}\)

Substituting these values in Eq. (i), we get

⇒  \(T_2=\sqrt{\frac{4 l_1}{l_1}} \times 2=2 \times 2=4 \mathrm{~s}\)

Question 50. The damping force on an oscillator is directly proportional to the velocity. The units of the constant of proportionality are:

1. kg ms^-1
2. kg ms^-2
3. kg s^-1
4. kg s

Answer: 3. kg s^-1

It is given that force \(\propto\) velocity

⇒ \(F \propto V \)

F =K V

K = \(\frac{F}{V}\)

Unit of K =\(\frac{F}{V}=\mathrm{kg} \mathrm{s}^{-1}\)

Question 51. When an oscillator completes 100 oscillations its amplitude reduces to \(\frac{1}{3}\) of the initial value. What will be its amplitude when it completes 200 oscillations?

1. \(\frac{1}{8}\)
2. \(\frac{2}{3}\)
3. \(\frac{1}{6}\)
4. \(\frac{1}{9}\)

Answer: 1. \(\frac{1}{8}\)

Let \(a_0\) be the initial amplitude and b be the damping constant

The used formula is a=\(a_0 e^{-b t}\)

In Ist case : t=100 T and a=\(\frac{a_0}{3}\)

⇒ \(\frac{a_0}{3} =a_0 e^{-b(100 T)}\)

⇒ \(e^{-b \times 100 T} =\frac{1}{3}\)

In 2nd case : t =200 T

a = \( a_0 e^{-200 b T}\)

a = \(a_0\left(e^{-100 b T}\right)^2\)

a = \(a_0\left(\frac{1}{3}\right)^2\)

a = \(\frac{a_0}{9}\)

Question 52. In case of a forced vibration, the resonance peak becomes very sharp when the:

1. damping force is small
2. restoring force is small
3. applied periodic force is small
4. the quality factor is small

Answer: 1. The damping force is small

Less damping gives a taller and narrower resonance peak.

Kinetic Theory

Question 1. The volume occupied by the molecules contained 4.5 kg water at STP, if the intermolecular forces vanish away is:

1. 5.6 x 10⁶ m³
2. 5.6 x 10³ m³
3. 5.6 x 10^-3m³
4. 5.6 m³

Answer: 4. 5.6 m³

At STP, \(\mathrm{T}=273 \mathrm{~K}, \mathrm{P}=10^5 \mathrm{~N} / \mathrm{m}^2\)

Number of moles of water,\(\mathrm{n} =\frac{\text { mass of water }}{\text { molecular weight of water }}\)

= \(\frac{4.5}{1.8 \times 10^{-2}}\)=250

Using equation, \(\mathrm{PV}=\mathrm{nRT}\)

= \(\frac{\mathrm{nRT}}{\mathrm{P}}=\frac{250 \times 8.3 \times 273}{10^5}\)

= \(5.6 \mathrm{~m}^3\)

Question 2. A given sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule of the gas is m. Which of the following gives the density of the gas?

1. \(\frac{P}{(k T)}\)
2. \(\frac{P m}{(k T)}\)
3. \(\frac{P}{(k T V)}\)
4. mkT

Answer: 2. \(\frac{P m}{(k T)}\)

If, m = mass of gas

v = Volume of gas

⇒ \(\rho=\frac{m}{V}\)= Density of gas

Pressure P =\(\frac{1}{2} \rho V_{\text {rms }}^2\)

= \(\frac{1}{3} \rho \frac{3 R T}{M_0}=\frac{\rho R T}{M_0}\)

⇒ \(\left\{\text { Where, } V_{\text {rms }}=\sqrt{\frac{3 R T}{K N_A T}}\right\}\)

⇒ \(\rho =\frac{P M_0}{R T}=\frac{P M N A}{K N_A T}\)

∴ \(\rho =\frac{P m}{K T}\)

Read and Learn More NEET Physics MCQs

Question 3. In the given (V-T) diagram, what is the relation between pressure p₁ and p₂.

1. P2 = P₁
2. P₂>P₁
3. P₂<P₁
4. Cannot be predicted

Answer: 3. P2<P1

As we know,

PV = nRT

⇒ \(\frac{\mathrm{V}}{\mathrm{T}}=\frac{\mathrm{nR}}{\mathrm{P}}\)

The slope of the graph \(\propto \frac{1}{P}\).

Question 4. At 10°C the value of the density of a fixed mass of an ideal gas divided by its pressure is x. At 110°C this ratio is:

1. x
2. \(\frac{383}{283} x\)
3. \(\frac{10}{110} x\)
4. \(\frac{283}{383} x\)

Answer: 4. \(\frac{283}{383} x\)

Using equation,

PV = nRT

or \(\frac{P V}{M}=\frac{1}{M_0} R T\)

or \(\frac{P}{\rho} =\frac{R T}{M_0} \)

r = \(\frac{\rho}{P}=\frac{M}{R T}\)

∴ \(\frac{\rho}{P} \propto \frac{1}{T}\)

So, \(\frac{r_2}{r_1}=\frac{T_1}{T_2}=\frac{273+10}{273+110}=\frac{283}{383}\)

or \(r_2=\frac{283}{383} r_1\)

Question 5. The equation of state for 5 g of oxygen at a pressure P and temperature T, when occupying a volume V, will be (where R is the gas constant):

1. PV= (5/32)RT
2. PV= 5RT
3. PV= (5/2)RT
4. PV= (5/16)RT

Answer: 1. PV= (5/32)RT

We know that, PV = nRT

n=\(\frac{m}{\text { molecular mass }}=\frac{5}{32}\)

P V=\(\left(\frac{5}{32}\right) R T \)

Question 6. Three containers of the same volume contain three different gases. The masses of the molecules are m₁, m_2, and m₃ and the number of molecules in their respective containers are N₁, N_2, and N₃. The gas pressure in the containers is p₁, p_2, and p₃ respectively. All the gases are now mixed and put in one of these containers. The pressure p of the mixture will be:

1. \(p<\left(p_1+p_2+p_3\right)\)
2. p=\(\frac{p_1+p_2+p_3}{3}\)
3. p=\(p_1+p_2+p_3\)
4. \(p>\left(p_1+p_2+p_3\right)\)

Answer: 1. \(p<\left(p_1+p_2+p_3\right)\)

According to Dalton’s law of partial pressure, the total pressure exerted by a mixture of gases that do not interact with each other is equal to the sum of the partial pressures that each would impose if alone occupied the same volume at the given temperature. When various gases are combined in one container, the mixture’s pressure P will be P=P₁+P₂+P₃

Question 7. A ideal gas equation can be written as:\(P=\frac{\rho R T}{M_0}\) where, ρ and M₀ are respectively :

1. mass density, the mass of the gas
2. number density, molar mass
3. mass density, molar mass
4. number density, the mass of the gas

Answer: 3. mass density, molar mass

The ideal gas equation is given by:

P V = nRT

P V =\(\frac{m}{\mathrm{M}} R T\)

P =\(\frac{m}{V}\left(\frac{R T}{M_0}\right)\)

P =\(\rho\left(\frac{R T}{M_0}\right)\)

∴ \(\mathrm{P} =\frac{m}{\mathrm{~V}}\)

Where, \(\rho \text { and } \mathrm{M}_{\mathrm{o}}\) are mass density and molar mass respectively.

Question 8. The average thermal energy for a monoatomic gas is (where Kg is Boltzmann constant and T is the absolute temperature.):

1. \(\frac{3}{2} K_B T\)
2. \(\frac{5}{2} K_B T\)
3. \(\frac{7}{2} K_B T\)
4. \(\frac{1}{2} K_B T\)

Answer: 1. \(\frac{3}{2} K_B T\)

The average thermal energy of the system with a degree of freedom is equal to its average energy.

Average thermal energy =\(\frac{f}{2} K_B \cdot T\)

For monoatomic gas f=3

Average thermal energy =\(\frac{3}{2} K_B \cdot T\)

Where, \(K_B\)= Boltzmann constant

and T = absolute temperature.

Question 9. An increase in the temperature of a gas-filled container would lead to:

1. increase in its kinetic energy
2. decrease in its pressure
3. decrease in intermolecular distance
4. increase in its mass.

Answer: 1. increase in its kinetic energy

An increase in the temperature of a gas-filled container leads to an increase in its kinetic energy.

Question 10. At what temperature will the RMS speed of oxygen molecules become just sufficient for escaping from the Earth’s atmosphere? Given : mass of oxygen molecule m= 2.76 x 10^-26 kg; Boltzmann’s constant kB= 1.38 x 10^-23Jk

1. 5.016 x 10⁴ K
2. 8.326 x 10⁴ K
3. 2.508 x 10⁴ K
4. 1.254 x 10⁴ K

Answer: 2. 8.326 x 10⁴ K

Escape velocity is the minimum velocity with which when a body is projected, so as to enable it to just overcome the gravitational pull of that surface i.e.Earth

Given: \(k_B =1.38 \times 10^{-23} \mathrm{Jk}^{-1}\)

⇒ \(m_0 =2.76 \times 10^{-26} \mathrm{~g}\)

Escape Velocity, \(v_e=\sqrt{\frac{2 G M}{R}}=\sqrt{2 g R}\)

⇒ \(v_e =\sqrt{2 \times 9.8 \times 6.4 \times 10^6}\)

=\(11.2 \mathrm{kms}^{-1}=11200 \mathrm{~ms}^{-1}\)

⇒ [Since radius of earth R=6.4 \(\times 10^6 \mathrm{~m}]\)

Say at temperature T it attains escape velocity

⇒ \(v_e =\sqrt{\frac{3 K_B T}{m_{02}}}\)

11200 =\(\sqrt{\frac{3 K_B T}{m_{02}}}\)

T =\(\frac{\left(11.2 \times 10^3\right)^2 \times 2.76 \times 10^{-26}}{3 \times 1.38 \times 10^{-23}}\)

∴ T =8.326 \(\times 10^4 \mathrm{k}\)

Question 11. The molecules of a given mass of a gas have r.m.s. velocity of 200 ms^-1 at 27°C and 1.0 x 10s Nm^-2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 x 105 Nm^-2, the RMS velocity of its molecules in ms^-1 is:

1. \(\frac{400}{\sqrt{3}}\)
2. \(\frac{100 \sqrt{2}}{3}\)
3. \(\frac{100}{3}\)
4. \(100 \sqrt{2}\)

Answer: 1. \(\frac{400}{\sqrt{3}}\)

Given, \(v_{\mathrm{rms}}=200 \mathrm{~ms}^{-1}, T_1=300 \mathrm{~K}, P_1=10_5 \mathrm{~N} / \mathrm{m}^2\)

⇒ \(T_2=400 \mathrm{~K}, P_2=0.05 \times 10^5 \mathrm{~N} / \mathrm{m}\)

We know that, \(v_{\text {rms }}=\sqrt{\frac{3 k_B T}{m}}\)

⇒ \(v_{\text {rms }} \propto \sqrt{T}\)

⇒  \(\frac{v_{27}}{v_{127}}=\sqrt{\frac{27+273}{127+273}}=\sqrt{\frac{300}{400}}=\frac{\sqrt{3}}{2}\)

∴ \(v_{\mathrm{rms}}=\frac{200 \times 2}{\sqrt{3}} \mathrm{~m} / \mathrm{s}=\frac{400}{\sqrt{3}} \mathrm{~m} / \mathrm{s}\)

Question 12. In a vessel, the gas is at pressure P, if the mass of all the molecules is halved of their speed is double, then the resultant pressure will be :

1. 2P
2. P
3. P/2
4. 4P

Answer: 1. 2P

The equation of pressure is, \(P=\frac{1}{3} \frac{m \mathrm{~N}}{V} v_{r m s}^2\)  Equation 1

where, m = mass of each molecule

N = number of molecules

Z = volume of the gas

According to the question: Mass of all molecules is halved and velocity is double then

⇒ \(P^{\prime} =\frac{1}{3}\left(\frac{m}{2}\right) \times \frac{N}{V} \times\left(2 v_{r m s}\right)^2 \)

=\(\frac{2}{3} \frac{m N}{V} v_{r m s}^2 \)

=\(2 \times \frac{1}{3} \frac{m \mathrm{~N}}{V} v_{r m s}^2\)

=2 P

compare with eq (1), P’ = 2P

Question 13. The pressure of a gas is raised from 27°C to 927°C. The root mean square speed:

1. Is\(\sqrt{\left(\frac{927}{27}\right)}\)times the earlier value
2. remains the same
3. gets halved
4. gets doubled

Answer: 3. gets halved

The square root of the mean of the squares of the random velocities of individual molecules in a gas is defined as RMS speed.

RMS speed is calculated by using the Maxwell distribution law \(C_{\mathrm{rms}}=\sqrt{\left(\frac{3 k T}{m}\right)}\)

⇒  \(C_{\mathrm{rms}} \propto \sqrt{T}\)

For two different cases i.e. at two different temperatures,

⇒  \(\frac{\left(C_{\text {rms }}\right)_1}{\left(C_{\text {rms }}\right)_2}=\sqrt{\frac{T_1}{T_2}}\)

Here, \(T_1=27^{\circ} \mathrm{C}=300 \mathrm{~K}\)

⇒  \(T_2=927^{\circ} \mathrm{C}=1200 \mathrm{~K}\)

⇒  \(\frac{\left(C_{\mathrm{rms}}\right)_1}{\left(C_{\mathrm{rms}}\right)_2}=\sqrt{\frac{300}{1200}}=\frac{1}{2}\)

⇒  \(\left(C_{\mathrm{rms}}\right)_2=2\left(C_{\mathrm{rms}}\right)_1\)

∴ Hence, the RMS speed will be doubled.

Question 14. The relation between pressure (p) and energy (E) of a gas is:

1. p=\(\frac{2}{3} E\)
2. p=\(\frac{1}{3} E\)
3. p=\(\frac{3}{2} E\)
4. p=3 E

Answer: 1. p=\(\frac{2}{3} E\)

We have, pressure exerted by gas molecules,

p=\(\frac{1}{3} \rho_{\mathrm{v}}^{-}\)  →  Equation 1

where, \(\rho\)= density of gas

⇒ \(\bar{v}\)= average velocity of gas molecules, or  \(p=\frac{2}{3} n \cdot \frac{1}{2} m_{\mathrm{v}} ( since \rho=mn)\)

Here, \(\frac{1}{2} m \overline{\mathrm{v}}\)= average kinetic energy of a gas molecule \((\overline{\mathrm{KE}})\)

Therefore,p=\(\frac{2}{3} n \overline{\mathrm{KE}}\)

If the total number of gas molecules in volume V is N then, Therefore, No. of gas molecules per unit volume

n = \(\frac{N}{V} \)

P = \(\frac{2}{3} \cdot \frac{N}{V}\left(\frac{1}{2} m v^2\right)\)

{or} P V = \(\frac{2}{3} N(\overline{\mathrm{KE}}) \quad\left[K E=\frac{1}{2} m v^2\right]\)

Also, from Eq. (1),

P V=\(\frac{2}{3} \cdot \frac{1}{2} \rho v^2\)

Here, \(\frac{1}{2} \rho v^{-2}\)= average kinetic energy of the gas per unit volume.

Therefore, P=\(\frac{2}{3} E\)

Question 15. According to the kinetic theory of gases, at absolute zero temperature:

1. water freezes
2. liquid helium freezes
3. molecular motion stops
4. liquid hydrogen freezes

Answer: 4. liquid hydrogen freezes

According to the kinetic theory of gases, the pressure P exerted by one mole of an ideal gas,

P = \(\frac{1}{3} \frac{M}{V} c^2\)

or \(\frac{1}{3} M c^2\)

or \(\frac{1}{3} M c^2=\mathrm{RT}\)  → Equation 1

where c is the root mean square velocity of gas. From (1), when T = 0, c = 0

Hence, the absolute zero temperature can be defined as the temperature at which the root mean square velocity of the gas molecules falls to zero. At absolute zero temperature, the molecular motion comes to a stop.

Question 16. Match Column – 1 and Column – 2 and choose the correct match from the given choices:

1. 1 – C,  2  – A,   3 – D,  4 -B
2. 1 – B,  2  –  C    3 – D, 4 – A
3. 1 – B,  2 – A,   3 – D, 4 – C
4. 1 – C,  2 – B,   3 – A,  4 – D

Answer: 3. 1 – B,  2 – A,   3 – D, 4 – C

The RMS velocity is, \(v_{r m s}=\sqrt{\frac{3 R T}{M}}\)

The pressure exerted by an ideal gas is \(\frac{1}{3} m n v^{-2}\).

Average kinetic energy of a molecule \(\frac{3}{2} k_B T\).

The total internal energy of 1 mole of a diatomic gas, U=\(\frac{5}{2} R T\).

Question 17. The volume ( V) of a monoatomic gas varies with its temperature (7), as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to B is:

1. \(\frac{1}{3}\)
2. \(\frac{2}{3}\)
3. \(\frac{2}{5}\)
4. \(\frac{2}{7}\)

Answer: 3. \(\frac{2}{5}\)

The given graph shows that Volume V \(\propto\) temperature

⇒ \(\frac{V}{T}\)= Constant

This is an isobaric process,

We know that Work done, \(\Delta W=P \Delta V=n R \Delta T\)  →  Equation 1

Absorbed heat, \(\Delta Q=n C_P D T=n C_p\left(T_B-T_A\right)\)  → Equation 2

For monoatomic gas, f=3

⇒ \(C_P=\left(R+\frac{3}{2} R\right)=\frac{5}{2} R\)

Then eq.(2) becomes,

⇒ \(\Delta \mathrm{Q}=n\left(\frac{5}{2} R\right)\left(T_B-T_A\right)\)  Equation 2

Divided eq. (1) by (2) we write,

⇒ \(\frac{\Delta \mathrm{W}}{\Delta \mathrm{Q}}=\frac{n R[T_B-T_A]}{n(\frac{5}{2}}\)

∴ \(R\left[T_B-T_A\right]=\frac{2}{5}\)

Question 18. A gas mixture consists of 2 moles of O₂ and 4 moles of Ar at temperature T. Neglecting all vibrational modes, the total internal energy of the system is:

1. ART
2. 15RT
3. 9RT
4. 11 RT

Answer: 4. 11 RT

Total internal energy of system = Internal energy of oxygen molecules + internal energy of argon molecules

= \(\frac{f_1}{2} \eta_1 R T+\frac{f_2}{2} \eta_2 R T\)

= \(\frac{5}{2} \times 2 R T+\frac{3}{2} \times 4 R T=11 R T\)

Question 19. A mass of diatomic gas (y = 1.4) at a pressure of 2 atm is compressed adiabatically so that its temperature rises from 27° C to 927° C. The pressure of the gas at the final state is:

1. 28 atm
2. 68.7 atm
3. 256 atm
4. 8 atm

Answer: 3. 256 atm

⇒ \(T_1=273+27=300 \mathrm{~K}\)

⇒ \(T_2=273+927=1200 \mathrm{~K}\)

for adiabatic process, \(P V^\gamma\) = constant

⇒ \(P\left(\frac{T}{P}\right)^\gamma\) = constant {because P V=n R T}

⇒ \(\frac{P_2}{P_1} =\left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\gamma-1}}\)

⇒ \(P_2 =P_1\left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\gamma-1}}\)

= \(2\left(\frac{1200}{300}\right)^{\frac{1.4}{1.4-1}}\)

= \((2)(4)^{\frac{1.4}{1.4-1}}\)

= 256 atm

Question 20. The gas carbon-monoxide (CO) and nitrogen (N₂) at the same temperature have kinetic energies E₁ and E₂ respectively. Then:

1. E₁ = E₂
2. E₁ > E₂
3. E₁ < E₂
4. E₁ and E₂ cannot be compared.

Answer: 1. E₁ = E₂

Since carbon monoxide (CO) and nitrogen (N₂) are diatomic gases. So, their kinetic energies will be equal, i.e. E₁ = E₂.

Question 21. An ideal gas at 27°C is compressed adiabatically to \(\frac{8}{27}\)of its original volume. The rise in temperature is [Given: \(\gamma=\frac{5}{3}\)

1. 475° C
2. 402° C
3. 275° C
4. 375° C

Answer: 4. 375° C

In an adiabatic process, \(P V^\gamma\)= constant  → Equation 1

Where, P= pressure, V= volume and \(\gamma\)= atomicity of gas,

Now from the ideal gas equation, P V=R T  (for one mole)

or P=\(\frac{R T}{V}\) (where, R= gas constant) →  Equation  2

From Eqs. (1) and (2), we get,

⇒ \(\left(\frac{R T}{V}\right) V^\gamma\) = constant

⇒ \(T V^{\gamma-1}\) = constant

For two different cases of temperature and volume of a gas,

⇒ \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)

or \(\frac{T_2}{T_1}=\left(\frac{V_1}{V_2}\right)^{\gamma-1}\)  →   Equation  3

Given, \(T_1 =27^{\circ} \mathrm{C}\)

= 27+273=300 \(\mathrm{~K}\)

And \(\frac{V_2}{V_1}=\frac{8}{27}\), \(\gamma=\frac{5}{3}\)

Substituting these values in Eq. (3), we get,

⇒ \(\frac{T_2}{300}=\left(\frac{27}{8}\right)^{5 / 3-1}\)

or \(\frac{T_2}{300}=\left[\left(\frac{3}{2}\right)^3\right]^{2 / 3}\)

or \(\frac{T_2}{300}=\left(\frac{3}{2}\right)^2=\frac{9}{4}\)

⇒ \(T_2=\frac{9}{4} \times 300=675 \mathrm{~K}=402^{\circ} \mathrm{C}\)

Thus, rise in temperature, = \(T_2-T_1\)

= \(402^{\circ} \mathrm{C}-27^{\circ} \mathrm{C}=375^{\circ} \mathrm{C}\)

Question 22. The degrees of freedom of a molecule of a triatomic gas are:

1. 2
2. 4
3. 6
4. 8

Answer: 3. 6

• A triatomic gas molecule tends to rotate along one of three coordinate axes. As a result, it possesses six degrees of freedom, 3 of which are translational and 3 of which are rotational.
• A triatomic molecule with a high enough temperature has 2 vibrational degrees of freedom. But, as there is no temperature requirement given. So, by simply assuming a triatomic gas molecule at room temperature has 6 degrees of freedom.
• Thus,(3 translational degrees + 3 rotational degrees) at room temperature.

Question 23. A diatomic gas initially at 18°C is compressed adiabatically to one-eight of its original volume. The temperature after compression will be:

1. 18° C
2. 668.4° K
3. 395.4° C
4. 144° C

Answer: 2. 668.4° K

⇒ \(T V^{\gamma-1}\)= constant

For two different cases, of temperature and volume of the gas.

⇒ \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)  →  Equation 1

Given, the initial temperature,

⇒ \(T_1=18^{\circ} \mathrm{C}=291 \mathrm{~K}\)

Let initial volume, \(V_1\)=V then the final volume, \(V_2=\left(\frac{1}{8}\right)\) V Given,

Putting these values in Eq. (1),

⇒ \(T_2 =291\left(\frac{V_1}{V_2}\right)^{\gamma-1}=291\left(\frac{V}{\left(\frac{1}{8}\right) V}\right)^{7 / 5-1}\)

= 668.4 \(\mathrm{~K}\)

Question 24. The number of translational degrees of freedom for a diatomic gas is:

1. 2
2. 3
3. 5
4. 6

Answer: 2. 3

Several degrees of freedom of a dynamical system is calculated by subtracting the number of independent relations from the total number of coordinates required to describe the positions of the system’s constituent particles.

If I is the number of particles in the system, R is the number of independent relations between the particles, and N is the system’s degree of freedom, then, N =3A – R

Every monoatomic, diatomic, and triatomic gas has three translational degrees of freedom

Question 25. The value of \(\left(\gamma=\frac{C_P}{C_V}\right)\)for hydrogen, helium and another
ideal diatomic gas X (whose molecules are not rigid but have an additional vibration mode), are respectively equal to :

1. \(\frac{7}{5}, \frac{5}{3}, \frac{9}{7}\)
2. \(\frac{5}{3}, \frac{7}{5}, \frac{9}{7}\)
3. \(\frac{5}{3}, \frac{7}{5}, \frac{7}{5}\)
4. \(\frac{7}{5}, \frac{5}{3}, \frac{7}{5}\)

Answer: 1. \(\frac{7}{5}, \frac{5}{3}, \frac{9}{7}\)

⇒ \(\gamma=\frac{C_P}{C_V}\)

where \(C_P\)= molar heat capacity constant pressure and \(C_V\)= molar heat capacity at constant volume Also, \(C_P=C_V+R\) (from Mayer’s relation)

⇒ \(C_V=\frac{f}{2} R\) (where, f= degree of freedom)

⇒ \(C_P=\left(\frac{f}{2}+1\right) R\)

So eq. (1) becomes,

⇒ \(\gamma=1+\frac{2}{f}\)

For hydrogen gas, which is diatomic, the degree of freedom is 5 (3 translational, 2 rotational).

⇒ \(\gamma=1+\frac{2}{5}=\frac{7}{5}\)

For helium gas, which is monatomic, the degree of freedom is 3 ( 3 translational only).

⇒ \(\gamma=1+\frac{2}{3}=\frac{5}{3}\)

The diatomic gas X also has vibrational motion, so the degree of freedom is 7 (3 translational, 2 rotational, and 2 vibrational)

∴ \(\gamma=1+\frac{2}{7}=\frac{9}{7}\)

Question 26. One mole of an ideal monatomic gas undergoes a process described by the equation pV₃ =constant. The heat capacity of the gas during this process is:

1. \(\frac{3}{2} R\)
2. \(\frac{5}{2} R\)
3. 2R
4. R

Answer: 4. R

From the polytropic process,

⇒ \(P V^x\)= constant

Heat capacity in the polytropic process is given by,

C=\(C_y+\frac{R}{1-x}\)

From question, \(\mathrm{PV}^3\) = constant

x = 3  →  Equation 1

and also gas is monoatomic,

So,\(C_V=\frac{3}{2} R \)  →  Equation 2

from above formula, C =\(\left[\frac{3}{2} R+\frac{R}{1-3}\right]\)

=\(\frac{3}{2} R-\frac{R}{3}\)=R

Question 27. The ratio of the specific heat \(\frac{C_P}{C_V}=\gamma\) in terms of degrees of freedom (n) is given by:

1. \(\left(1+\frac{1}{n}\right)\)
2. \(\left(1+\frac{n}{3}\right)\)
3. \(\left(1+\frac{2}{n}\right)\)
4. \(\left(1+\frac{n}{2}\right)\)

Answer: 3. \(\left(1+\frac{2}{n}\right)\)

We know that specific heat at constant volume is given by,\(C_V=\frac{n}{2} R\)

Where, n = degree of freedom

R = gas constant

And \(C_P-C_V\)=R  [Mayer’s formula]

⇒\(C_P=\frac{n}{2} R+R=R\left(1+\frac{n}{2}\right)\)

⇒ \(\gamma=\frac{C_P}{C_V}=\frac{R\left(1+\frac{n}{2}\right)}{\frac{n}{2} R}\)

= \(\frac{2}{n}+1 \)

Question 28. The molar-specific heats of an ideal gas at constant pressure and volume and denoted by Cp and Cv respectively.  If \(\gamma=\frac{C_P}{C_V}\) and R is the universal gas constant then Cv is equal to:

1. \(\frac{1+\gamma}{1-\gamma}\)
2. \(\frac{R}{(\gamma-1)}\)
3. \(\frac{(\gamma-1)}{R}\)
4. \(\gamma^R\)

Answer: 2. \(\frac{R}{(\gamma-1)}\)

As we know, \(C_P-C_V\) = R and \(\gamma=\frac{C_P}{C_V}\)

⇒ \(C_V =\frac{\mathrm{R}}{\gamma-1}\)

Question 29. The amount of heat energy required to raise the temperature of 1 g of helium at NTP, from T₁K to T₂K is:

1. \(\frac{3}{8} N_a k_B\left(T_2-T_1\right)\)
2. \(\frac{3}{2} N_a k_B\left(T_2-T_1\right)\)
3. \(\frac{3}{4} N_a k_B\left(T_2-T_1\right)\)
4. \(\frac{3}{4} N_a k_B\left(\frac{T_2}{T_1}\right)\)

Answer: 1. \(\frac{3}{8} N_a k_B\left(T_2-T_1\right)\)

Number of moles of 1 \(\mathrm{~g} \mathrm{He}=\frac{1}{4}\)

The amount of heat energy required to raise the temperature of the gas is,

⇒ \(\Delta \mathrm{Q}=n \mathrm{C}_{\mathrm{V}} \Delta \mathrm{T}\)

Here, n=\(\frac{1}{4}, C_V =\frac{3}{2} R\)

= \(\left(\frac{1}{4}\right)\left(\frac{3}{2} R\right)\left(T_2-T_1\right)\)

= \(\frac{3}{8} k_B N_A\left(T_2-T_1\right) . (k_3=\frac{R}{N a})\)

Question 30. The molar specific heat at constant pressure of an ideal gas is (7/2) R. The ratio of specific heat at constant pressure to that at constant volume is:

1. 9/7
2. 7/5
3. 8/7
4. 5/7

Answer: 2. 7/5

Molar-specific heat at constant pressure,

⇒ \(C_P=\frac{7}{2} R\)

We know that, \(C_P-C_V=R\)

⇒ \(C_V =C_P-R \)

= \(\frac{7}{2} R-R=\frac{5}{2} R\)

from (1) and (2),

∴ \(\frac{C_P}{C_V}=\frac{7}{5}\)

Question 31. One mole of an ideal gas at an initial temperature of TK does 6R joules of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be:

1. (T+2X)K
2. {T-2A)K
3. (T+4)K
4. (T-4)K

Answer: 1. (T+2X)K

We know that work done in the adiabatic process is:

W=\(\frac{-1}{V-1}\left(P_f V_f-P_i V_i\right)\)

⇒ \(6 R=\frac{-1}{\frac{5}{3}-1} R\left(T_f-T_i\right)\)  {Since,P V=n R T}

⇒ \(T_f-T_i=-4\)

∴ \(T_f=(T-4) \mathrm{K}\)

Question 32. If for a gas, \(\frac{R}{C_{\mathrm{v}}}\)= 0.67, this gas is made up of molecules which are:

1. diatomic
2. mixture of diatomic and polyatomic molecules
3. monoatomic
4. polyatomic

Answer: 3. monoatomic

Since, \(C_{\mathrm{v}}=\frac{R}{0.67} \approx 1.5 R=\frac{3}{2} R\)

Hence, it is the case of monoatomic gases

Question 33. For hydrogen gas Cp – Cv = a and oxygen gas C_p – C_v = b, the relation between a and b is given by:

1. a= 16b
2. 16b = a
3. a = 4b
4. a = b

Answer: 4. a = b

Since hydrogen and oxygen are diatomic gases and C_p – C_v = R is the same for all gases. Hence, a: b, assuming C_p and C_v are gram molar specific heats.

Question 34. For a certain gas, the ratio of specific heat is given to be y = 1.5, for this gas:

1. \(C_v=\frac{3 R}{J}\)
2. \(C_p=\frac{3 R}{J}\)
3. \(C_p=\frac{5 R}{J}\)
4. \(C_p=\frac{5 R}{J}\)

Answer: 2. \(C_p=\frac{3 R}{J}\)

We have,\(\gamma=\frac{C_P}{C_V}\)

Given,\(\gamma=1.5=\frac{3}{2}\)

⇒ \(C_V=\frac{2}{3} C_P\)

From Mayer’s formula, \(C_P-C_V =\frac{R}{J}\)

⇒ \(C_P-\frac{2}{3} C_P =\frac{R}{J}\)

⇒ \(\frac{C_P}{3} =\frac{R}{J}\)

∴ \(C_P =\frac{3 R}{J}\)

Question 35. At 27°C a gas is compressed suddenly such that its pressure becomes \(\left(\frac{1}{8}\right)\)of original pressure. Final temperature will be \(\left(\gamma=\frac{5}{3}\right)\)

1. 420 K
2. 300 K
3. -142° C
4. 327 K

Answer: 3. -142° C

In an adiabatic process, PVϒ = k(a constant)  →  Equation 1

where, P = pressure and V = volume and ϒ =atomicity of gas

Again from standard gas equation,\(P V^\gamma =n R T\)

V =\(\frac{R T}{P}\)

Putting the value of V in Eq. (1), we get

⇒ P \(\frac{R^\gamma T^\gamma}{p^\gamma}\)=k or

⇒ \(P^{1-\gamma} T^\gamma=\frac{k}{R^\gamma}\)= another constant or

⇒ \(P^{1-\gamma} T^\gamma\)= constant

For two different cases,

⇒ \(P_1{ }^{1-\gamma} T_1{ }^\gamma=P_2{ }^{1-\gamma} T_2{ }^\gamma\)

⇒ \(\left(\frac{T_2}{T_1}\right)^\gamma =\left(\frac{P_1}{P_2}\right)^{1-\gamma}\)

Here, \(P_2 =\left(\frac{1}{8}\right) P_I\)

⇒ \(T_1 =27^{\circ} \mathrm{C}=273+27=300 \mathrm{~K}\)

⇒ \(T_2 =?, \gamma=\frac{5}{3}\)

⇒ \(\left(\frac{T_2}{300}\right)^{5 / 3} =(8)^{1-5 / 3}=(8)^{-2 / 3}\)

⇒ \(T_2 =130.6 \mathrm{~K}\)

∴\(T_2 =-142^{\circ} \mathrm{C}\)

Question 36. The mean free path X for a gas, with molecular diameter d and number density n, can be expressed as:

1. \(\frac{1}{\sqrt{2} n \pi d^2}\)
2. \(\frac{1}{\sqrt{2} n^2 \pi d^2}\)
3. \(\frac{1}{\sqrt{2} n^2 \pi^2 d^2}\)
4. \(\frac{1}{\sqrt{2} n \pi d}\)

Answer: 1. \(\frac{1}{\sqrt{2} n \pi d^2}\)

The mean free path \(\lambda\) for gas, with molecular diameter d and number density n can be expressed on \(\frac{1}{\sqrt{2} n \pi d^2}\)

Question 37. The mean free path of a molecule of a gas (radius r) is inversely proportional to the:

1. \(r^3\)
2. \(r^2\)
3. r
4. \(\sqrt{r}\)

Answer: 2. \(r^2\)

Mean free path, \(\lambda=\frac{1}{\pi n r^2}\)

∴ \(\lambda \propto \frac{1}{r^2}\)

Question 38. At constant volume, temperature is increased, then:

1. collision on walls will be less.
2. the number of collisions per unit of time will increase.
3. collisions will be in straight lines.
4. collisions will not change.

Answer: 2. the number of collisions per unit of time will increase.

The average velocity of the gas molecules increases as the temperature rises. As a result, more molecules collide with the walls. Hence, the number of collisions per unit time will increase.

Question 39. A polyatomic gas with n degrees of freedom has a mean energy per molecule given by:

1. \(\frac{n k T}{N}\)
2. \(\frac{n k T}{2 N}\)
3. \(\frac{n k T}{2}\)
4. \(\frac{3 k T}{2}\)

Answer: 3. \(\frac{n k T}{2}\)

According to the law of energy equipartition, for any dynamical system in thermal equilibrium, the total energy is distributed equally across all degrees of freedom, and the energy associated with each molecule per degree of freedom equals 12kT. The mean energy per molecule for a polyatomic gas with n degrees of freedom is \(\frac{1}{2} n k T\).

Where,k = Boltzmann

constant n = degree of freedom,

and T- Temperature

Thermodynamics

Question 1. A sample of 0.1 g of water at 100° C and normal pressure (1.013 x 10⁵ Nm^-2) requires 54 cal of heat energy to convert to steam at 100°C. If the volume of the steam produced is 167.1 cc, the change in internal energy of the sample is:

1. 42.2 J
2. 208.7 J
3. 104.3 J
4. 84.5 J

Answer: 2. 208.7 J

From the question, Heat spent during the conversion of a sample of water at \(100^{\circ}\) to steam is,

⇒ \(\Delta \mathrm{Q} =54 \mathrm{cal}=54 \times 4.18 \mathrm{~J}=225.72 \mathrm{~J}\)

⇒ \(P =1.013 \times 10^5 \mathrm{Nm}^{-2}\)

Work done \(\Delta W=P \Delta V=P\left[V_{\text {steam }}-V_{\text {water }}\right]\)

Here, \(V_{\text {steam }}=|167| c c=1 \times 10^{-6} \mathrm{~m}^3\)

⇒ \(V_{\text {water }} =0.1 \mathrm{~g}=0.1 c c=0.1 \times 10^{-6} \mathrm{~m}\)

⇒ \(\Delta W =1.013 \times 10^5\left[(167.1-0.1) \times 10^{-6}\right]\)

=\(1.013 \times 167 \times 10^{-1}=(16.917)\)

We also know that,

⇒ \(\Delta Q =\Delta U+\Delta W\)

⇒ \(\Delta U =\Delta Q-\Delta W=2.25 .72-16.917\)

=208.75

Question 2. Liquid oxygen at 50 K is heated to 300 K at a constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?

Answer: 1.

The given graph in option (1) shows the variation of temperature with time.

Question 3. The internal energy change in a system that has absorbed 2 KCal of heat and done 500 J of work is:

1. 8900 J
2. 6400 J
3. 5400 J
4. 7900 J

Answer: 4. 7900 J

Using the first law of thermodynamics, \(\Delta U=\Delta Q-\Delta W\)

ΔU = ΔQ-ΔW

= 2 x 4.2 x 1000-500 = 8400 – 500 = 7900 J

Read and Learn More NEET Physics MCQs

Question 4. 110 J of heat is added to a gaseous system, whose internal energy is 40 J, then the amount of external work done is:

1. 150 J
2. 70 J
3. 110 J
4. 40 J

Answer: 2. 70 J

From the first law of thermodynamics,

⇒ \(\Delta Q=\Delta U+\Delta W\)

where, \(\Delta Q\)= heat given

⇒ \(\Delta U\)= change in internal energy

⇒ \(\Delta W\)= work done

Here,\(\Delta Q = 110 \mathrm{~J}\)

⇒ \(\Delta U =40 \mathrm{~J}\)

⇒ \(\Delta W =\Delta Q-\Delta U\)

=110-40=70 \(\mathrm{~J}\)

Question 5. The first law of thermodynamics is a consequence of the conservation of:

1. work
2. energy
3. heat
4. All of these

Answer: 2. energy

According to the first law of thermodynamics, when some amount of heat (dQ) is supplied to a system capable of doing external work, the amount of heat absorbed by the system (dQ) equals the sum of the increase in the internal energy of the system (dU) due to temperature rise and the external work done by the system (dW) in expansion.

dQ =dU + dW

This law is the law of conservation of energy that applies to every process in nature.

Question 6. One mode of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. The change in internal energy of the gas during the transition is:

1. 20 J
2. -12 kJ
3. 20 kJ
4. -20 kJ

Answer: 4. -20 kJ

We know, \(\Delta U=n C_V+\Delta T\)

= \(\mathrm{n}\left(\frac{5 \mathrm{R}}{2}\right)\left(\mathrm{T}_{\mathrm{B}}-\mathrm{T}_{\mathrm{A}}\right) \quad\left[\text { for diatomic, } \mathrm{CV}=\frac{5 \mathrm{R}}{2}\right]\)

= \( \frac{5 \mathrm{nR}}{2}\left(\frac{\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}}{\mathrm{nR}}-\frac{\mathrm{P}_{\mathrm{A}} \mathrm{V}_{\mathrm{A}}}{\mathrm{nR}}\right)\mathrm{PV}=\mathrm{nRT}]\)

= \(\frac{5}{2}\left(\mathrm{P}_{\mathrm{B}} \mathrm{V}_{\mathrm{B}}-\mathrm{P}_{\mathrm{A}}-\mathrm{V}_{\mathrm{A}}\right)=\frac{5}{2}\left(2 \times 10^3 \times 6-5 \times 10^3 \times 4\right)\)

=\(\frac{5}{2}\left(-8 \times 10^3\right)=20 \mathrm{~kJ}\)

=\(n\left(\frac{5 R}{2}\right)\left(T_B-T_A\right)\) [for diatomic gas, \(\mathrm{Cv}\)=0

Question 7. If \(C_P\) and \(C_V\) denote the specific heats per unit mass of and ideal gas of molecular weight M, then

1. \(C_{P-} C_{V=R / M}{ }^2\)
2. \(C_P-C_{V=R}\)
3. \(C_{P-} C_{V=R / M}\)
4. \(C_{P-} C_{V=M R}\)

Where R is the molar gas constant.

Answer: 3. \(C_{P-} C_{V=R / M}\)

Let \(C_V\) and \(C_P \)be molar-specific heats of the ideal gas at constant volume and constant pressure, respectively, and then

⇒ \(\mathrm{C}_{\mathrm{P}}=\mathrm{MC}_{\mathrm{p}} \text { and } \mathrm{C}_{\mathrm{V}}=\mathrm{MC}_{\mathrm{V}}\)

⇒ \(\mathrm{C}_{\mathrm{P}}-\mathrm{C}_{\mathrm{V}}=\mathrm{R}\)

⇒ \(\mathrm{MC}_{\mathrm{P}}-\mathrm{MC}_{\mathrm{V}}=\mathrm{R}\)

∴ \(\mathrm{C}_{\mathrm{P}}-\mathrm{C}_{\mathrm{V}}=\mathrm{R} / \mathrm{M}\)

Question 8. If the ratio of the specific heat of a gas at constant pressure to that of the constant volume is y, the change in internal energy of a mass of gas when the volume changes from V to 2V at constant pressure P is:

1. \(\frac{R}{(\gamma-1)}\)
2. PV
3. \(\frac{P V}{(\gamma-1)}\)
4. \(\frac{\gamma P V}{(\gamma-1)}\)

Answer: 3. \(\frac{P V}{(\gamma-1)}\)

Change in internal energy of a gas having atomicity \(\gamma\) is given by,

⇒ \(\Delta U=\frac{1}{(\gamma-1)}\left(p_2 V_2-p_1 V_1\right)\)

Given,\(V_1=V, V_2=2 V\)

So,\(\Delta U =\frac{1}{\gamma-1}[p \times 2 V-p x V]\)

= \(\frac{1}{\gamma-1} p V=\frac{p V}{\gamma-1}\)

Question 9. One mole of an ideal gas requires 207 J heat to raise the temperature by 10 K when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same 1 K, the heat required is:

1. 198.7 J
2. 29 J
3. 215.3 J
4. 124 J

Answer: 4. 124 J

Using \(C_p-C_v=R,\)

⇒ \(\mathrm{C}_{\mathrm{p}}\) is heat needed for raising by 10 \(\mathrm{~K}\).

⇒ \(\mathrm{C}_{\mathrm{p}}=20.7 \mathrm{~J} / \mathrm{mole} \mathrm{K}\)

Given R = 8.3 J/mole K

For raising by 10 K = 124 J

Question 10. A cylinder contains hydrogen gas at a pressure of 249 kPa and temperature 27°C. Its density is (R = 8.3 J mol^-1 k^-1):

1. 0.5 kg / m³
2. 0.2 kg / m³
3. 0.1 kg / m³
4. 0.2 kg / m³

Answer: 2. 0.2 kg / m³

Given: \(\mathrm{P}=249 \mathrm{kPa} ; \mathrm{T}=27^{\circ} \mathrm{C}, \mathrm{M}=2 \times 10^{-3} \mathrm{~kg}\)

Equation of state,

P V=\(\eta R T or P M=\delta \mathrm{RT} \quad\left[\eta=\frac{m}{M}\right]\)

⇒ \(\delta =\frac{P M}{R T}\)

= \(\frac{\left(249 \times 10^3\right)\left(2 \times 10^{-3}\right)}{8.3 \times 300}=0.2 \mathrm{~kg} / \mathrm{m}^3\)

Question 11. Which of the following is not a thermodynamical function?

1. Enthalpy
2. Work done
3. Gibb’s energy
4. Internal energy

Answer: 2. Work done

• Certain specific thermodynamic variables, such as pressure p, volume V, temperature T, and entropy S, can be used to describe the thermodynamic state of a homogeneous system.
• Any two of these four variables are independent and once they’re known, the others can be calculated. As a result, there are just two independent variables, with the others working as functions.
• Certain relationships are essential for a thorough understanding of the system, and we introduce some thermodynamic functions, which are functions of variables p, V, T, and S. Thermodynamic functions are classified into four categories.

1. Internal energy (U)
2. Helmholtz tunction (F)
3. Enthalpy (H)
4. Gibb’s energy (G)

Hence, the work done is not a thermodynamic function

Question 12. An ideal gas undergoes four different processes at the same initial state as shown in the figure below. These processes are adiabatic, isothermal, isobaric, and isochoric. The curve which represents the adiabatic process among 1,2, 3, and 4 is:

1. 1
2. 2
3. 3
4. 4

Answer: 2. 2

Curve 4 is an isobaric process because the pressure is constant. Curve I is isochoric because the volume is constant. Curve 3 is smaller than curve 2.

Question 13. In which of the following processes, heat is neither absorbed nor released by a system?

1. Adiabatic
2. Isobaric
3. Isochoric
4. Isothermal

Answer: 1. Adiabatic

In an adiabatic process, there is no exchange of heat of the system with its surroundings. Thus in the adiabatic process P₁V₁ and T change but ΔQ = 0 or entropy remains a constant process, I – Isochoric, volume is constant\(\left(\Delta S=\frac{\Delta Q}{T}\right)\)

Question 14. Thermodynamic processes are indicated in the following diagram:

Match The Following:

1. P → A, Q → C, R → D, S → B
2. P → C, Q → A, R → D, S → B
3. P → C, Q → D, R → B, S → A
4. P → D ,Q → B, R → A, S → C

Answer: 1. P → A, Q → C, R → D, S→ B

Process, 1 – Isochoric, volume is constant.

2: Adiabatic, the slope of curve II is more than the slope of curve 3

3: Isothermal

4: Isobaric, Pressure is constant. repeat

Question 15. The volume (V) of a monatomic gas varies with its temperature (7), as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to state B, is:

1. \(\frac{2}{5}\)
2. \(\frac{2}{3}\)
3. \(\frac{1}{3}\)
4. \(\frac{2}{7}\)

Answer: 1. \(\frac{2}{5}\)

In the process 1, volume is constant.

Process 1 → Isochoric; P → C

As slope of curve 2 is more than the slope of curve III.

Process 2 → Adiabatic and

Process 3 -→ Isothermal

Q → A, R→D

In process 4, pressure is constant.

Process 4 → Isobaric; S → B

Question 16. A gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process until its volume is again reduced to half. Then:

1. compressing the gas through adiabatic.
2. compressing the gas isothermally or adiabatically will require the same amount of work.
3. which of the cases (whether compression through . isothermal or through an adiabatic process) requires more work will depend upon the atomicity of the gas.
4. compressing the gas isothermally will require more to be done.

Answer: 2. compressing the gas isothermally or adiabatically will require the same amount of work.

⇒ \(\mathrm{W}_{\text {ext }} =\text { negative of area with volume }- \text { axis }\)

∴ \(W(\text { adiabatic }) >W \text { (isothermal })\)

Question 17. The figure below shows two paths that may be taken by a gas to go from a state A to a state C. In process AB, 400 J of heat is added to the system, and in process, BC, 100 J of heat is added to the system. The heat absorbed by the system in process AC will be:

1. 380 J
2. 500 J
3. 460 J
4. 300 J

Answer: 3. 460 J

From the diagram, We see that the initial and final points are the same.

Case 1 :

So, \(\Delta U_{A \rightarrow B \rightarrow C}=\Delta U_{A \rightarrow C}\) →  Equation 1

A \(\rightarrow B \)(Isochoric process)

⇒ \(d \mathrm{~W}_{\mathrm{A} \rightarrow \mathrm{B}}\)=0 and

⇒ \(d \mathrm{Q}=d \mathrm{U}=d \mathrm{~W}\)

∴ \(d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{B}}=d \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{B}}=400 \mathrm{~J}\)

Case 2 : \(\mathrm{B} \rightarrow \mathrm{C}\) is isobaric process

⇒ \(d \mathrm{Q}_{\mathrm{B} \rightarrow \mathrm{C}} =d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}+d \mathrm{~W}_{\mathrm{B} \rightarrow \mathrm{C}}\)

= \(d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}+\mathrm{P} \Delta \mathrm{V}_{\mathrm{B} \rightarrow \mathrm{C}}\)

⇒ \(100 =d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}+6 \times 10^4\left(2 \times 10^{-3}\right)\)

∴ \(d \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}} =100-120=-20 \mathrm{~J}\)

Using eq. (1),

⇒ \(\Delta \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C}}=\Delta \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{C}}\)

⇒ \(\Delta \mathrm{U}_{\mathrm{A} \rightarrow \mathrm{B}}+\Delta \mathrm{U}_{\mathrm{B} \rightarrow \mathrm{C}}\)

= \(d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{C}}-\mathrm{dW}_{\mathrm{A} \rightarrow \mathrm{C}}\)

⇒ \(400+(-20)=d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{C}}-\left(\mathrm{P} \Delta \mathrm{U}_{\mathrm{A}}+\text { Area } \Delta_{\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C}}\right)\)

⇒ \(d \mathrm{Q}_{\mathrm{A} \rightarrow \mathrm{C}}=380[2 \times 10^4 \times 2 \times 10^{-3}+\).

⇒ \(\left.\frac{1}{2} \times 2 \times 10^{-3} \times 4 \times 10^4\right]\)

∴ \(d Q_{\mathrm{A} \rightarrow \mathrm{C}}=460 \mathrm{~J}\)

Question 18. A thermodynamic system undergoes the cyclic process ABCD as shown in the figure. The work done by the system in the cycle is:

1. \(p_0 V_0\)
2. \(2 p_0 V_0\)
3. \(\frac{p_0 V_0}{2}\)
4. zero

Answer: 4. zero

According to the question,

Work done in the cyclic process: Area bound by the closed configuration

Area of closed configuration \(\left\{2\left[\frac{1}{2}\left(\frac{\mathrm{V}_0}{2}\right) \times \mathrm{P}_0\right]+\left[-2\left\{\frac{1}{2}\left(\frac{\mathrm{V}_0}{2}\right) \times \mathrm{P}_0\right\}\right]\right\}=0\)

Question 19. An ideal gas is compressed to half its initial volume using several processes. Which of the processes results in the maximum work done on the gas?

1. Adiabatic
2. Isobaric
3. Isochoric
4. Isothermal

Answer: 1. Adiabatic

Work done = Area under P-V graph So large work is in adiabatic Here,

∴ \(W_{\text {adiabatic }}>W_{\text {isothermal }}>W_{\text {isobaric }}\)

Question 20. A Monoatomic gas at a pressure p, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is (take \(\lambda=\frac{5}{3}\)):

1. 64p
2. 32p
3. \(\frac{P}{64}\)
4. 16p

Answer: 3. \(\frac{P}{64}\)

Using Ideal Gas Equation, P =\(\frac{n R T}{V}\)

⇒ \(P_1 =\frac{n R T}{2 V}=\frac{P}{2}\)

For isothermal expansion, \(P V =P_1 \times 2 V \)

⇒ \(P_1 =\frac{P}{2}\)

For adiabatic expansion, \(P V^r\) = Constant

⇒ \(P_1 V_1^r= P_2 V_2^r\)

⇒ \(P_2 =[2 V]^{5 / 3}=P_2[16]^{5 / 3} \)

⇒ \(P^2 =\frac{P}{2}\left[\frac{2 V}{16 V}\right]^{\frac{5}{3}}=\frac{P}{2}\left[\frac{1}{8}\right]^{\frac{5}{3}}\)

= \(\frac{P}{2} \times 0.0312=0.0156 P\)

=  \(\frac{P}{64}\)

Question 21. A gas is taken through the cycle A →  B → C → A as shown. What is the net work done by the gas?

1. 200J
2. 1000J
3. Zero
4. -200J

Answer: 2. 1000J

Net work done = Area of triangle

= \(\frac{1}{2} \times\left[(7-2) \times 10^{-3}\right]\left[(6-2) \times 10^5\right] =1000 \mathrm{~J}\)

Question 22. During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its temperature.
The ratio of \(\frac{C_P}{C_V}\) for the gas is:

1. \(\frac{4}{3}\)
2. 2
3. \(\frac{5}{3}\)
4. \(\frac{3}{2}\)

Answer: 4. \(\frac{3}{2}\)

According to the question, \(P T^{-3}\)= Constant  →  Equation 1

For an adiabatic process, \(PT \|-r\)= constant  →   Equation 2

compare equation (1) and (2), we get

⇒ \(\frac{r}{1-r}=-3\)

r =\(-3+3 r \text { or } r=\frac{3}{2}\)

As, r =\(\frac{C_P}{C_V}\):

∴ \(\mathrm{C}_{\mathrm{P}} / \mathrm{C}_{\mathrm{V}} =\frac{3}{2}\)

Question 23. A system is taken from state a to state c by two paths act and abc as shown in the figure. The internal energy a is U₂ – 10 J. Along the path adc the amount of heat absorbed is δQ₁ = 50 J, and the work obtained δW₁ = 20 J whereas, along the path ABC, the heat absorbed δQ₂ = 36 J. The amount of work along the path ABC is:

1. 10 J
2. 12 J
3. 36 J
4. 6 J

Answer: 4. 6 J

According to \(1^{\text {st }}\) law of thermodynamics

⇒ \(\delta Q=\delta V+\delta W\)

Along the path adc, \(\delta U_1=\delta Q_1-\delta W_1\)

=50-20

= 30 \(\mathrm{~J}\)

then path ABC , \(\delta U_2=36-\delta W_2\)

Since the change in Internal energy in path independence

So,\(\delta U_1 =\delta U_2\)

⇒ \(30 \mathrm{~J} =36 \mathrm{~J}-\delta W_2\)

⇒ \(\delta W_2 =36 \mathrm{~J}-30 \mathrm{~J} \)

=6 \(\mathrm{~J}\)

Question 24. Which of the following relations does not give the equation of an adiabatic process, where terms have their usual meaning?

1. \(P^{1-\gamma} T^\gamma\)= constant
2. \(P V^\gamma\)= constant
3. \(T V^{\gamma-1}\)= constant
4. \(P^\gamma T^{1-\gamma}\)= constant

Answer: 4. \(P^\gamma T^{1-\gamma}\)= constant

Adiabatic process \(\rightarrow \)Heat does not exchange between system surrounding

⇒ \(P V^\gamma\)= constant →  Equation 1

Ideal gas equation P V=n R T

P =\(\frac{n R T}{V}=\frac{n R T}{V} \quad V^\gamma\)= constant

⇒ \(T V^\gamma-1\) = constant  →  Equation 2

PV = nRT

V =\(\frac{n R T}{P}\) { Put in eq. (1) }

Again PV=n R T

⇒ \(P\left(\frac{n R T}{P}\right)^\gamma\) = constant

⇒ \(P^{1-\gamma} T^\gamma\) = constant

So, option (d) does not give the relation.

Question 25. A thermodynamic system is taken through the cycle ABCD as shown in the figure. Heat rejected by the gas during the cycle is:

1. 2 PV
2. 4 PV
3. \(\frac{1}{2} P V\)
4. PV

Answer: 1. 2 PV

From the question,

For a given cyclic process AV= 0

Q = W

W =- Area enclosed in the curve

= AB AD

= (2P-P) x (3V- V)

=-p x 2V

Heat rejected = 2 PV

Question 26. An ideal gas goes from state A to state B via three different processes as indicated in the p-V diagram. If Q₁, Q₂, Q₃ indicate the heat absorbed by the gas along the three processes and ΔU₁, ΔU₂, ΔU₂ indicate the change in internal energy along the three processes respectively, then:

1. Q₁ > Q₂ > Q₃ and ΔU₁ = ΔU₂ = ΔU₃
2. Q₃ > Q₂ > Q₁ and ΔU₁ = ΔU₂ = ΔU₃
3. Q₁ = Q₂ = Q₃ and ΔU₁ > ΔU₂ > ΔU₃
4. Q₃ > Q₂ > Q₁ and ΔU₁ > ΔU₂ > ΔU₃

Answer: 1. Q₁ > Q₂ > Q₃ and ΔU₁ = ΔU₂ = ΔU₃

According to the question,

⇒ \(\Delta U_1=\Delta U_2=\Delta U_3\)

⇒ \(Q_1>Q_2>Q_3\)

because, \(\Delta Q=\Delta W+d U\)

change in internal energy is independent of the path.

Question 27. One mole of an ideal gas goes from an initial state A to a final state B via two processes: It first undergoes isothermal expansion from volume V to 3 V and then its volume is reduced from 3V to V to constant pressure. The correct PL-V diagram representing the two processes is

Answer: 4.

Given that, gas A → B

firstly isothermal expansion = V to 3 V

then volume reduced from 3 V to V at constant pressure

(1) For isothermal expansion,

T= constant

PV= NRT = constant

PV= constant

Hence hyperbolic curve

(2) Now for isobaric compression,

P = constant

PV= nRT

∴ straight line. Hence option (D) is correct.

Question 28. During an isothermal expansion, a confined ideal gas does – 150 J of work against its surroundings. This implies that:

1. 150 J of heat has been removed from the gas.
2. 300 J of heat has been added to the gas
3. No heat is transferred because the process is isothermal.
4. 150 J of heat has been added to the gas.

Answer: 3. No heat is transferred because the process is isothermal

From the first law of thermodynamics

⇒ \(\Delta U=\Delta \mathrm{Q}+\Delta W\)

for isothermal process \(\Delta U\)=0

⇒ \(\Delta \mathrm{Q}=-\Delta W \)

⇒ \(\Delta Q\)=-(-150)=150

∴ Here \(\Delta\) Q is positive means heat is added to gas.

Question 29. A mass of diatomic gas (γ = 1.4) at a pressure of 2 atmospheres is compressed adiabatically so that its temperature rises from 27°C to 927°C. The pressure of the gas in the final state is:

1. 8 at
2. 28 atm
3. 68.7 atm
4. 256 atm

Answer: 4. 256 atm

For an adiabatic process, \(\frac{T^\gamma}{P^{\gamma-1}}\)= constant

⇒ \(\left(\frac{T_i}{T_f}\right)^\gamma=\left(\frac{P_i}{P_f}\right)^{\gamma-1}\)

Here,\( P_f=P_i\left(\frac{T_i}{T_f}\right)^{\frac{\gamma}{\gamma-1}}\)

⇒ \(\mathrm{~T}_{\mathrm{i}}=27^{\circ} \mathrm{C}=300 \mathrm{~K}\),

⇒ \(\mathrm{~T}_{\mathrm{f}}=927^{\circ} \mathrm{C}=1200 \mathrm{~K}\)

⇒ \(\mathrm{P}_{\mathrm{i}}=2 \mathrm{~atm}, \gamma\) = 1.4

Substituting these values in eqn (i), we get

⇒ \(P_f =(2)\left(\frac{1200}{300}\right)^{\frac{1.4}{1.4-1}}=(2)(4)^{1.4 / 0.4}\)

= \(2\left(2^2\right)^{7 / 2}=(2)(2)^7=2^8=256 \mathrm{~atm}\)

Question 30. If AU and AW represent the increase in internal energy and work done by the system respectively in a thermodynamical process, which of the following is true?

1. ΔU = – ΔW, in adiabatic process
2. ΔU= ΔW, in an isothermal process
3. ΔU = ΔW, in a adiabatic process
4. ΔU = -ΔW, in an isothermal process

Answer: 1. ΔU = – ΔW, in adiabatic process

From the first law of thermodynamics,

⇒ \(\Delta Q=\Delta U+\Delta W\)

for adiabatic process, \(\Delta \mathrm{Q}\)=0

∴ \(\Delta U=-\Delta W\)

Question 31. In a thermodynamic process which of the following statements is not true?

1. In an adiabatic process, the system is insulated from the surroundings
2. In an isochoric process, pressure remains constant
3. In an isothermal process, the temperature remains constant
4. In an adiabatic process PV₁ = constant

Answer: 2. In an isochoric process pressure remains constant

In an isochoric process, volume remains constant.

Question 32. If Q, E, and W denote respectively the heat added, change in internal energy, and the work done in a closed cycle process, then:

1. W= 0
2. Q=W=0
3. E = 0
4. g = 0

Answer: 3. E = 0

In the cyclic process, since initial and final states are of the same internal energy is a state function therefore initial and final internal energies are also the same. So, the charge in internal energy is the same, hence E = 0

Question 33. Two moles of an ideal gas are taken in a cyclic process abcda. During the process ab and cd temperatures are 500 K and 300 K respectively. Calculate heat absorbed by the system (in 2 = 0.69 and R = 8.3 J/mol-K).

1. 2290.3 J
2. 2209.3 J
3. 2029.3 J
4. 2293.3 J

Answer: 1. 2290.3 J

From the diagram, it is clear that:

⇒ \(Q_{a b c d a}=Q_{a b}+Q_{b c}+Q_{c d}+Q_{d a}\)

Here a b, b c, c d, and d a represent isothermal expansion, isochoric compression, isothermal compression, and isochoric expansion respectively,

⇒ \(Q_{b c} =Q_{d a}\)

⇒ \(Q_{a b c d a} =Q_{a b}+Q_{c d}\)

⇒ \(Q_{a b c d a} =Q_{a b}+Q_{c d}\)

= \(\eta R T_1 \log \left[\frac{2 V_0}{V_0}\right]+\mu R T_2 \log \left[\frac{V_0}{2 V_0}\right]\)

= \(2 \times 8.3 \times 0.09(500-300)\)

= 2290.3 J

Question 34. A sample of gas expands from volume V₁ to V₂. The amount of work done by the gas is greatest when the expansion is:

1. adiabatic
2. isobaric
3. isothermal
4. equal in all the above cases

Answer: 2. isobaric

The P-V diagram for the isobaric, isothermal, and adiabatic processes of an ideal gas is shown in the graph below,

In thermodynamics, for some volume change, the work done is maximum for the curve having maximum area enclosed with the volume axis.

The area enclosed by the curve,

⇒ (Slope of curve ) alpha

⇒ \((\text { slope })_{\text {isobaric }}<(\text { slope })_{\text {isothermal }}<(\text { slope })_{\text {adiabatic }}\)

⇒ \((\text { Area })_{\text {isobaric }}>(\text { Area })_{\text {isothermal }}>(\text { Area })_{\text {adiabatic }}\)

Hence, the work done is maximum in the isobaric process.

⇒ \((\text { Slope })_{\text {adiabatic }} =-\gamma\left(\frac{P}{V}\right)\)

⇒ \(\text { and }(\text { Slope })_{\text {isothermal }} =-\frac{P}{V} \)

⇒ \((\text { Slope })_{\text {adiabatic }} =\gamma \times(\text { slope })_{\text {isothermal }}\)

The slope of the adiabatic curve is always steeper than that of the isothermal curve

Question 35. An ideal gas A and a real gas B have their volumes increased from V to 2V under isothermal conditions. The increase in internal energy:

1. will be the same in both A and B
2. will be zero in both the gases
3. of B will be more than that of A
4. of A will be more than that of B

Answer: 2. will be zero in both the gases

An isothermal change occurs when the pressure and volume of a gas change without the temperature changing. There is a free exchange of heat between the gas and its surroundings during such a transition.

T= constant, \(\Delta\)= 0

∴ So, internal energy (U) remains constant.

Question 36. A thermodynamic system is taken from state A to B along ACB and is brought back to A along BDA as shown in the diagram. The net work done during the complete cycle is given by the area:

1. \(p_1 A C B p_2 p_1\)
2. \(A C B B^{\prime} A^{\prime} A\)
3. A C B D A
4. \(A D B B^{\prime} A^{\prime} A\)

Answer: 3. A C B D A

Work done during path ACB = area ACBB’ A’ A

Work done during going from ACB and then to BDA path is = area ACB B’A’A – area BDAA’ B’ B

= area ACBDA

Question 37. A thermodynamic process is shown in the figure. The pressure and volumes corresponding to some points in the figure are:

⇒ \(P_A=3 \times 10^4 \mathrm{~Pa} ; V_A=2 \times 10^{-3} \mathrm{~m}^3 \)

⇒ \(P_B=8 \times 10^4 \mathrm{~Pa} ; V_D=5 \times 10^{-3} \mathrm{~m}^3\)

In the process, AB, 600 J of heat is added to the system. The change in internal energy of the system is process AC would be

1. 560 J
2. 800 J
3. 600 J
4. 640 J

Answer: 1. 560 J

Since AB is an isochoric process. So no work is done. \mathrm{BC} is isobaric process

⇒ \(\mathrm{W}=\mathrm{P}_{\mathrm{B}} \times\left(\mathrm{V}_{\mathrm{D}}-\mathrm{V}_{\mathrm{A}}\right)=240 \mathrm{~J}\)

⇒ \(\Delta \mathrm{Q}=600+200=800 \mathrm{~J}\)

Using \(\Delta \mathrm{Q}=\Delta \mathrm{U}+\Delta \mathrm{W}\)

∴ \(\Delta \mathrm{U}=\Delta \mathrm{Q}-\Delta \mathrm{W}=800-240=560 \mathrm{~J}\)

Question 38. The efficiency of an ideal heat engine working between the freezing point and boiling point of water is :

1. 6.25%
2. 20%
3. 26.8%
4. 12.5%

Answer: 3. 26.8%

We know that the efficiency of an ideal heat engine \(\eta=\left(1-\frac{T_2}{T_1}\right)\)

Where, \(T_1=100+273=373 \mathrm{~K}\)

⇒ \(T_2=0.273=273 \mathrm{~K}\)

Putting the value of \(T_1 and T_2\) in eq. (1), We get,

⇒ \(\eta =1-\frac{273}{373}=\frac{373-273}{373}=\frac{100}{373}\)

=0.268

Now, % \(\eta\) =0.268 x 100=26.8 %

Question 39. A heat engine has a source at a temperature of 527°C and a sink at a temperature of 127°C. If the useful work is required to be done by the engine at the rate of 800 W, then find the amount of heat absorbed by the sink per second from the source in calories. Also, find the efficiency of the heat engine.

1. \(381 \mathrm{cal} \mathrm{s}^{-1}, 50 \%\)
2. \(318 \mathrm{cal} \mathrm{s}^{-1}, 50 \%\)
3. \(381 \mathrm{cal} \mathrm{s}^{-1}, 45 \%\)
4. \(318 \mathrm{cal} \mathrm{s}^{-1}, 45 \%\)

Answer: 1. \(381 \mathrm{cal} \mathrm{s}^{-1}, 50 \%\)

From question, \(T_1=800 \mathrm{~K}, T_2=400 \mathrm{~K}\) and \(W=a_1-a_2=800 \mathrm{~W}\)

Work done per unit amount of heat absorbed is:

⇒ \(\frac{W}{Q_1} =\frac{T_2-T_2}{T_1}=\frac{800-900}{800}=\frac{1}{2}\)

⇒ \(\frac{800}{Q_1} =\frac{1}{2}\)

⇒ \(Q_1=1600 \mathrm{~W}\)

⇒ \(Q_1=\frac{1600}{4.2}=381 \mathrm{cal} \mathrm{s}^{-1}\)

∴ Efficiency, \(\eta=\frac{T_1-T_2}{T_1}=\frac{800-400}{800}=\frac{1}{2}\)= 50%

Question 40. The temperatures of the source and sink of a heat engine are 127°C and 27°C respectively. An inventor claims its efficiency to be 26%, then:

1. it is impossible
2. it is possible with a high probability
3. it is possible with a low probability
4. Data is insufficient

Answer: 1. it is impossible

Efficiency of heat engine is, \(\eta =1-\frac{T_2}{T_1}\) { or } \(\eta=\frac{T_1-T_2}{T_1}\)

⇒ T₁ = temperature of sink

⇒  T₂=Temperature of source

Given, T₁=273+127=400 K

⇒ T₂=273+27=300 K

⇒ \(\eta =\frac{400-300}{400}=\frac{100}{400}\)

=0.25 = 25 %

Hence, 26% efficiency is impossible for a given heat engine

Question 41. A refrigerator works between 4°C and 30°C. It is required to remove 600 calories of heat every second to keep the temperature of the refrigerated space constant. The power required is (Take, 1 cal = 4.2 Joules):

1. 23.65 W
2. 236.5 W
3. 2365 W
4. 2.365 W

Answer: 2. 236.5 W

According to the question, Temperature of source, \(T_1=30^{\circ} \mathrm{C}=30+273\)

⇒ \(T_1=303 \mathrm{~K}\)

Temperature of sink, \(T_2=4^{\circ} \mathrm{C}=4+273\)

⇒ \(T_2=277 \mathrm{~K}\)

We know that \(\frac{Q_1}{Q_2} =\frac{T_1}{T_2}\)

⇒ \(\frac{Q_2+W}{Q_2} =\frac{T_1}{T_2}\left\{ W=\mathrm{Q}_1-\mathrm{Q}_2\right\}\)

⇒ \(W T_2+T_2 Q_2 =T_1 Q_2 \)

⇒ \(W T_2 =T_1 Q_2-T_2 Q=Q_2\left(T_1-T_2\right)\)

W =\(\frac{Q_2}{T_2}\left(T_1-T_2\right)=Q_2\left(\frac{T_1}{T_2}-1\right)\)

=600 \(\times 4.2\left(\frac{303}{277}-1\right)\)

=600 \(\times 4.2 \times \frac{26}{277} \)

=236.5 \(\mathrm{~J}=\text { Retain }\)

Power =\(\frac{\text { Work done }}{\text { time }}\)

= \(\frac{236.5}{1}=236.5 \mathrm{~W}\)

Question 42. The temperature inside a refrigerator is t₂°C and the room temperature is t₁°C. The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be:

1. \(\frac{t_1}{t_1-t_2}\)
2. \(\frac{t_1+273}{t_1-t_2}\)
3. \(\frac{t_2+273}{t_1-t_2}\)
4. \(\frac{t_1+t_2}{t_1+273}\)

Answer: 2. \(\frac{t_1+273}{t_1-t_2}\)

If \(Q_1\)= amount of heat delivered to the room

W = electrical energy consumed

⇒ \(T_1 \)= room temperature =\(t_1+273 \)

⇒ \(T_2 \)= temp. of sink =\(t_2+273\)

Then, for the refrigerator,

⇒ \(\frac{Q_1}{W} =\frac{Q_1}{Q_1-Q_2}=\frac{T_1}{T_1-T_2}\)

⇒ \(\frac{Q_1}{1} =\frac{t_1+273}{\left(t_1+273\right)-\left(t_2+273\right)}\)

∴ \(Q_1 =\frac{t_1+273}{\left(t_1-t_2\right)}\)

Question 43. The coefficient of performance of a refrigerator is 5. If the temperature inside the freezer is – 20°C, the temperature of the surroundings to which it rejects heat is:

1. 31°C
2. 41°C
3. 11°C
4. 21°C

Answer: 1. 31°C

Coefficient of performance of the refrigerator

C.O.P =\(\frac{T_L}{T_H-T_L}\)

Where\( T_L\)= Lower temperature

⇒ \(T_H\)= Higher temperature

5 =\(\frac{T_L}{T_H-T_L}\)

⇒  \(T_H =\frac{6}{5} T_L\)

= \(\frac{6}{5} \times 253=303.6 \mathrm{~K}\)

= 31 \(\dot{\mathrm{C}}\)

Question 44. Which of the following processes is reversible?

1. Transfer of heat by conduction.
2. Transfer of heat by radiation.
3. Isothermal compression.
4. Electrical heating of a nichrome wire.

Answer: 3. Isothermal compression.

Isothermal compression is reversible. for example; Carnot cycle, heat engine.

Question 45. The efficiency of a Carnot engine depends upon:

1. the temperature of the sink only
2. the temperature of the source and sink
3. the volume of the cylinder of the engine
4. the temperature of the source only.

Answer: 2. the temperature of the source and sink

The efficiency of a camot engine is given by :\(\eta=1-\frac{T_2}{T_1}\)

Where, \(T_1\) = Temperature of source

⇒ \(T_2=\)= temperature of sink

This confirms that the efficiency of the Carnot engine depends upon the temperature of the source and also the temperature of the sink

Question 46. A Carnot engine having the efficiency of a heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at a lower temperature is:

1. 1 J
2. 90 J
3. 99 J
4. 100 J

Answer: 2. 90 J

In case of carnot engine, efficiency =\(\frac{\text { Work }}{\text { heat absorbed }}\)=\(\frac{W}{q_1}\)

⇒ \(\frac{W}{q_1} =\frac{1}{10}\)

⇒ \(\frac{10 \mathrm{~J}}{q_1} =\frac{1}{10}\)

⇒ \(q_1 =100 \mathrm{~J}\)

When the engine is reversed then\( W+q_2 =q_1 \)

⇒ \(10+q_2 \)=100

∴ \(q_2 =90 \mathrm{~J}\)

Question 47. Two Carnot engines A and B are operated in series. Engine A receives heat from the source at temperature T₁ and rejects the heat to the sink at temperature T. The second engine B receives the heat at temperature T and rejects to its sink at temperature T₂. For what value of T the efficiencies of the two engines are equal:

1. \(\frac{T_2-T_2}{2}\)
2. \(T_1 T_2\)
3. \(\sqrt{T_1 T_2}\)
4. \(\frac{T_1+T_2}{2}\)

Answer: 3. \(\sqrt{T_1 T_2}\)

We know that the efficiency of the Carnot engine,

⇒ \(\eta=1-\frac{T_2}{T_1}\)

Where, \(T_1\)= temperature of source

⇒ \(T_2\)= temp of sink

For engine A, \(\eta_{\mathrm{A}}=1-\frac{T}{T_1}\)

engine B, \(\eta_{\mathrm{B}}=1-\frac{T_2}{T}\)

From question, \(\eta_A =\eta_B\)

⇒ \(1-\frac{T}{T_1} =1-\frac{T_2}{T}\)

⇒ \(\frac{T}{T_1}=\frac{T_2}{T} =T^2\)

⇒ \(T^2 =T_1 T_2 \)

T =\(\sqrt{T_1 T_2}\)

Question 48. An engine has an efficiency of 1/6. When the temperature of the sink is reduced by 62°C, its efficiency is doubled. Temperatures of the source are:

1. 37°C
2. 62°C
3. 99°C
4. 124°C

Answer: 3. 99°C

Using the formula for efficiency, \(\eta =1-\frac{T_2}{T_1} \)

⇒ \(\frac{1}{6} =1-\frac{T_2}{T_1}\)

⇒ \(\frac{T_2}{T_1} =\frac{5}{6}\)

Since the temp. of the source remains unchanged,

⇒ \(2 \times \frac{1}{6} =1-\frac{T_2-60}{T_1}\)

⇒ \(\frac{1}{3} =1-\frac{\left(T_2-62\right)}{T_1}\)

⇒ \(\frac{2}{3} =\left[\frac{5}{2}-2\right] T_1 \)

⇒ \(T_1 =3 T_2-186\)

⇒ \({\left[\frac{5}{2}-2\right] T_1}\) =186

∴ \(T_1 =372 \mathrm{~K}=99^{\circ} \mathrm{C}\)

Question 49. A Carnot engine whose sink is at 300 K has an efficiency of 40%. By how much should the temperature of the source be increased to increase its efficiency by 50% of the original efficiency?

1. 380 K
2. 275 K
3. 325 K
4. 250 K

Answer: 4. 250 K

Efficiency of Carnot engine,

⇒ \(\eta =1-\frac{T_2}{T_1}\)

⇒ \(\frac{T_2}{T_1} =1-\eta\)

⇒ \(\frac{300}{T_1} =1-\frac{40}{100}=\frac{3}{5}\)

⇒ \(\mathrm{~T}_1 =500 \mathrm{~K}\) or

New efficiency, \(\eta^{\prime}=\eta+\frac{50}{100} \eta=\frac{3}{2} \eta=60 \%\)

⇒ \(\frac{T_2}{T_1}=1-\frac{60}{100}=\frac{2}{5} \)

⇒ \(T_1^{\prime}=\frac{5}{2} \times T_2=\frac{5}{2} \times 300=750 \mathrm{~K}\)

Increase in temperature of the source,

⇒ \(\Delta \mathrm{T}=T_1^{\prime}-T_1 \)

∴ \(\Delta \mathrm{T}=750-500=250 \mathrm{~K}\) .

Question 50. An ideal gas heat engine operates in a Carnot cycle between 227°C and 127°C. It absorbs 6 x 10⁴ cal of heat at higher temperatures. The amount of heat converted into work is:

1. 4.8 x 10⁴cals
2. 6 x 10⁴cals
3. 2.4 x 10⁴cals
4. 1.2 x 10⁴cals

Answer: 4. 1.2 x 10⁴cals

For a Carnot engine efficiency, \(\eta =1-\frac{T_2}{T_1}\)

= \(1-\frac{127+273}{227+273}\)

= \(1-\frac{400}{500}=\frac{1}{5}\)

Now, \( \eta =\frac{\text { Work Output }}{\text { Heat Output }}\)

= \(\frac{\mathrm{W}}{6 \times 10^4}\)

∴ \(\mathrm{~W} =\eta \times 6 \times 10^4 \)

= \(\frac{1}{5} \times 6 \times 10^4\)

= \(1.2 \times 10^4 \mathrm{cal}\).

Question 51. The efficiency of the Camot engine is 50% and the temperature of the sink is 500 K. If the temperature of the source is kept constant and its efficiency raised to 60%, then the required temperature of the sink will be:

1. 100 K
2. 600 K
3. 400 K
4. 500 K

Answer : 3. 400 K

⇒ \(\% \eta=\left(1-\frac{T_2}{T_1}\right) \times 100\)

For 50 \(\%, \frac{50}{100}=1-\frac{50}{11}\)

⇒ \(T_1=1000 \mathrm{~K}\)

aim for 60 \(\%, \frac{60}{100}=1-\frac{T_2}{1000}\)

∴ \(T_2=400 \mathrm{~K}\)

Question 52. The (W/Q) of a Camot engine is 1/6, now the temperature of the sink is reduced by 62°C, then this ratio becomes twice, therefore the initial temperature of the sink and source are respectively:

1. 33°C, 67°C
2. 37°C, 99°C
3. 67°C, 33°C
4. 97 K, 37 K

Answer: 2. 37°C, 99°C

⇒ \(\frac{1}{6}=-\frac{T_2}{T_1}{ or }\frac{5}{6}=\frac{T_2}{T_1}\)

Now,\(\frac{1}{3}=1-\frac{T_2-62}{T_1}=1-\frac{5}{6}+\frac{62}{T_1}\)

⇒ \(\mathrm{~T}_1=62 \times 6=372 \mathrm{~K}=99^{\circ} \mathrm{C}\)

and \(\mathrm{T}_2=310 \mathrm{~K}=37^{\circ} \mathrm{C}\)

Question 53. The efficiency of a Carnot engine operating between temperatures of 100°C and-23°C will be

1. \(\frac{100-23}{273}\)
2. \(\frac{100+23}{373}\)
3. \(\frac{100+23}{100}\)
4. \(\frac{100-23}{100}\)

Answer: 2. \(\frac{100+23}{373}\)

The efficiency of the Carnot engine is given by, \(\eta=1-\frac{T_2}{T_1}=\frac{T_1-T_2}{T_1}\)

Given, \(T_1\) = temperature of reservoir

= \(100+273=273 \mathrm{~K}\)

⇒ \(T_2\) = temperature of sink

=\(-23+273=250 \mathrm{~K}\)

Substituting in Eq. (1), we get,

\(\eta =\frac{373-250}{373}\)

=\(\frac{100+23}{373}=\frac{123}{373}\)

 

Thermal Properties of Matter

Question 1. Mercury thermometer can be used to measure temperature up to:

1. 260°C
2. 100°C
3. 360°C
4. 500°C

Answer: 1. 260°C

A mercury thermometer is a liquid thermometer that uses the homogeneous variation in volume of a liquid as a temperature. Mercury is opaque and bright, making it easy to see in the glass tube, and it is a good heat conductor, soon reaching the temperature of the hot bath. A mercury thermometer can be used to measure temperatures up to 300°C or so because mercury begins to evaporate at 367°C.

Question 2. A Centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°. What is the fall in temperature as registered by the Centigrade thermometer?

1. 80°
2. 60°
3. 40°
4. 30°

Answer: 3. 40°

The relation between the Celsius scale and the Fahrenheit scale is \(\frac{C}{100}=\frac{F-32}{180}\)

Putting value of F=\(140^{\circ}\), we get

⇒ \(\frac{C}{100}=\frac{140-32}{180}\)=0.6

C = 60°

Hence, Fall in temperature = Temperature of boiling water – final temperature

100°C – 60°C = 40°C

Question 3. A copper rod of 88 cm and an aluminium rod of unknown length have their increase in length independent of increase in length independent of increase in temperature. The length of aluminium rod is:  \(\alpha_{\mathrm{Cu}}=1.7\times10^{-5}\mathrm{~K}^{-1},\alpha_{\mathrm{Al}}=2.2 \times 10^{-5} \mathrm{~K}^{-1}\)

1. 113.9 cm
2. 88 cm
3. 68 cm
4. 6.8 cm

Answer: 3. 68 cm

According to the question,

⇒ \(L_w=l_w\left(1+\alpha_w \Delta T\right)\)    →  Equation 1

⇒ \(L_{\mathrm{cu}}=l_{\mathrm{cu}}\left(l+\alpha_{\mathrm{cu}} \Delta t\right)\)  →  Equation 2

⇒ \(L_{\mathrm{A} l}=l_{\mathrm{A} l}\left(A+\alpha_{\mathrm{A} l} \Delta T\right)\)    →  Equation 3

From equation. (1) and equation (3),

Read and Learn More NEET Physics MCQs

⇒ \(L_{\mathrm{A} l}-L_{\mathrm{C} u}=L_{\mathrm{A} l}-L_{\mathrm{C} u}+\left(l_{\mathrm{A} l} \alpha_{\mathrm{A} l}-l_{\mathrm{C} u} \alpha_{\mathrm{Cu}}\right) \Delta T\)

Since, \(l_{\mathrm{A} l} \alpha_{\mathrm{A} l}=l_{\mathrm{C} u} \alpha_{C u}\)

⇒ \(l_{\mathrm{A} l}=\frac{l_{C u} \alpha_{\mathrm{Cu}}}{\alpha_{\mathrm{A} l}}\)

= \(\frac{8.8 \times 1.7 \times 10^{-5}}{2.2 \times 10^{-5}}=68 \mathrm{~cm}\)

∴ \(l_{\mathrm{Al}}=68 \mathrm{~cm}\)

Question 4. Coefficient of linear expansion of brass and steel rods and \(\alpha_I \text { and } \alpha_2\). Length of brass and steel rods are \(\mathrm{l}_1\text { and } I_2\) respectively. If I₁-I₂ is maintained the same at all temperatures, which one of the following relations holds good?

1. \(\alpha_1 l_2^2=\alpha_1{ }^2 l_2^2\)
2. \(\alpha_1{ }^2 l_2=\alpha_2^2 l_1\)
3. \(\alpha_1 l_1=\alpha_2 l_2\)
4. \(\alpha_1 l_2=\alpha_2 l_1\)

Answer: 3. \(\alpha_1 l_1=\alpha_2 l_2\)

The change in length for both rods should be the same,

⇒ \(\Delta l_1 =\Delta l_2\)

⇒ \(l_1 \alpha_1 \Delta T =l_2 \alpha_2 \Delta T\)

∴ \(l_1 \alpha_1 =l_2 \alpha_2\)

Question 5. The value of the coefficient of volume expansion of glycerin is \(5 \times 10^{-4} \mathrm{~K}^{-1}\). The fractional change in the density of glycerin for a rise of 40°C in its temperature is:

1. 0.015
2. 0.020
3. 0.025
4. 0.010

Answer: 2. 0.020

The value of coefficient of volume expansion of glycerin is =\(5 \times 10^{-4} \mathrm{~K}^{-1}\)

We know that, \(d_f=\frac{d_i}{(1+V \Delta \mathrm{T})}\)

Fractional change =\(\frac{d_i-d_f}{d_f}=1-\frac{d_f}{d_i}\)

= \(1-(1+V \Delta T)^{-1}=1-(1-V \Delta T)\)

⇒ \(\left\{\mathrm{Q}(1+x)^n \approx 1+n x\right\}\)

= V \(\Delta T=5 \times 10^{-4} \times 40\)=0.020

Question 6. The density of water at 20°C is 998 kg/m³ and at 40°C 992 kg/m³. The coefficient of volume expansion of water is:

1. 3 x 10^-4/°C
2. 2 x 10^-4/°C
3. 6 x 10^-4/°C
4. 10^-3/°C

Answer: 1. 3 x 10-4/°C

According to the question,

⇒ \(T_1=20^{\circ} \mathrm{C}, T_2=40^{\circ} \mathrm{C}\)

⇒ \(\rho_{20}=998 \mathrm{~kg} / \mathrm{m}^3 \rho_{40}=992 \mathrm{~kg} / \mathrm{m}^3\)

So, \(\rho_{\mathrm{T}_2}=\frac{\rho_{\mathrm{T}_1}}{(1+v \Delta T)}=\frac{\rho_{\mathrm{T}_1}}{1+v\left(T_2-T_1\right)}\)

Putting the values we get, 992=\(\frac{998}{1+\gamma(40-20)}\)

992=\(\frac{998}{1+20 \gamma}\)

⇒ \(992(1+20 \gamma)\) =998

1+20\( \gamma =\frac{998}{992} \)

⇒ \(20 \gamma =\frac{6}{992} \)

=\(\frac{6}{992} \times \frac{1}{20} =3 \times 10^{-1 \circ} \mathrm{C}\)

Question 7. (A)The weight of the sphere in the air is 50 g. Its weight is 40 g in a liquid, at a temperature of 20°C. When the temperature increases to 70°C, its weight becomes 45 g. Find: (1) the ratio of densities of liquid at given two temperatures is. (2) the coefficient of cubical expansion of liquid assuming that there is no expansion of the volume of a sphere.

Answer: 3.

(1) \(W_{\text {apparent }}=W_{\text {air }}-\rho V g\)

Let \(\rho_1=\text { density of liquid at } 20^{\circ} \mathrm{C}\)

40= \(50-V \rho_1 g \)

10= \(V \rho_1 g\)

Again, Let,\(\rho_2\)=density of liquid at  \(70^{\circ} \mathrm{C}\)

45= \(50-V \rho_2 g \)

5= \(V \rho_2 g \)

From eq. (1) and (2)

∴ \(\frac{\rho_1}{\rho_2}=\frac{2}{1}\)

(2)  Because \(\rho_2=\frac{M}{V_1(1+\gamma \Delta \theta)}=\frac{\rho_1}{(1+\gamma \Delta \theta)}\)

⇒ \(\frac{\rho_1}{\rho_2}=1+\gamma \Delta \theta\)

Since, \(\frac{\rho_1}{\rho_2}=2 \)

⇒ \(2=1+\gamma \Delta \theta \)

⇒ \(\gamma \Delta \theta=1\)

⇒ \(\gamma=\frac{1}{\Delta \theta}\)

∴ \(\gamma=\frac{1}{70-20}=\frac{1}{50}\)=0.02

Question 8. The quantities of heat required to raise the temperature of two solid copper spheres of radii \(r_1 \)  and \(r_2\left(r_1=1.5 r_2\right)\) through 1 K are in the ratio of:

1. \(\frac{9}{4}\)
2. \(\frac{3}{2}\)
3. \(\frac{5}{3}\)
4. \(\frac{27}{8}\)

Answer: 4. \(\frac{27}{8}\)

Heat required

Q = \(m c \Delta \mathrm{T}\)

= \(\left(\frac{4}{3} \pi r^3 \cdot \rho\right) c \Delta \mathrm{T}\)

Since \(\pi, \rho, c, \Delta\) t are constant.

⇒ \(\mathrm{Q} \propto r^3 \).

or, \(\frac{\mathrm{Q}_1}{\mathrm{Q}_2} =\frac{r_1^3}{r_2{ }^3}=\left(\frac{r_1}{r_2}\right)^3=\left(\frac{1.5 r_2}{r_2}\right)^3 \)

=\(\frac{27}{8}\)

Question 9. The thermal capacity of 40 g of aluminium (s-0.2 cal/g-K) is:

1. 168 J/K
2. 672 J/K
3. 840 J/K
4. 33.6 J/K

Answer: 4. 33.6 J/K

The thermal capacity of a body is defined as the amount of heat required to raise the temperature of the (whole) body through 1°C or 1 K.

The amount of heat energy required (ΔQ) to raise the temperature of mass m of a body through temperature range (ΔT) is, ΔQ = ms (ΔT)

where, s is the specific heat of the body, when ΔT = 1K,

ΔQ = thermal capacity

Thermal capacity = s x m x 1 = ms

Here,m = 40 g, s = 0.2 cal/g K

Thermal capacity = 40 x 0.2 = 8 cal/K

= 4.2 x 8 J/K = 33.6 J/K

Question 10. Steam at 100°C is passed into 20 g of water at 10°C. When water acquires a temperature of 80°C, the mass of water present will be [Take specific heat of water = 1 cal g^-1 C^-1latent heat of steam = 540 cal g^-1]:

1. 24 g
2. 31.5 g
3. 42.5 g
4. 22.5 g

Answer: 4. 22.5 g

Heat gain by water = heal loss of steam

20 x 1 x (80 – 10) = m x 540 + m x 1 x (100 – 80) 1400 = 560 m

m = 2.5 g

Total mass of water = 20 + 2.5 = 22.5 g

Question 11. A piece of ice falls from a height h so that it melts completely. Only one quarter of the heat produced is absorbed by the ice and all energy of ice gets converted into heat during its fall. The value of h is [Latent heat of ice is 3.4 x 10⁵ J/kg andg= 10 N/kg]:

1. 544 km
2. 136 km
3. 38 km
4. 34 km

Answer: 2. 136 km

Given that: mgH = ml

H = \(\frac{4 L}{g}=\frac{4 \times 3.4 \times 10^5}{10}\)

=136 km

Question 12. If 1 g of steam is mixed with 1 g of ice, then the resultant temperature of the mixture is:

1. 270°C
2. 230°C
3. 100°C
4. 50°C

Answer: 3. 100°C

The heat required by 1 g of ice at 0°C to melt into 1g of water at 0°c,

⇒ \(Q_1 \)=m L (L =latent heat of fusion )

=\(1 \times 80=80 \mathrm{cal}(L=80 \mathrm{cal} / \mathrm{g})\)

Heat required by 1 g of water at 0°C to boil at 100°C,

⇒ \(Q_2 =m c \Delta \mathrm{T}\) (c = specific heat of water) =

= 1 x 1(100-0)

⇒ \((c \left.=1 \mathrm{cal} / \mathrm{g}^{\circ} \mathrm{C}\right)\)

=100 cal

Thus, the total heat required by 1 g of ice to reach a temperature of 100°C,

⇒ \(Q=Q_1+Q_2=80+100=180 \mathrm{cal}\)

Heat available with 1 g of steam to condense into 1 g of water at 100°C,

⇒ \(Q^{\prime}= m L^{\prime}\)

⇒ \(\left(L^{\prime}\)= latent heat of vaporisation

= 1 x 536 cal ( L’ =536 call/g)

= 536 cal

The whole steam will not be condensed and ice will attain a temperature of 100°C. Thus, the temperature of the mixture is 100°C.

Question 13. The energy that will be ideally radiated by a 100kw transmitter in 1 hour is:

1. 36 x 10⁷J
2. 36 x 10⁴J
3. 36 x 10³J
4. 36 x 10⁵J

Answer: 1. 36 x 10⁷J

Power, \(\mathrm{P}=100 \mathrm{kw}=100 \times 10^3 \mathrm{~W}\) ;

Time, t = 1 hour =\(3600 \mathrm{~s}\)

Energy, \(\mathrm{E}=\mathrm{P} \times \mathrm{t} =100 \times 10^3 \times 3600\)

= \(36 \times 10^7 \mathrm{~J}\)

Question 14. A deep rectangular pond of surface area A, containing water (density = p specific heat capacity = 5), is located in a region where the outside air temperature is steady value at – 26°C. The thickness of the ice layer in the pond, at a certain instant x. Taking the thermal conductivity of ice as K, and its specific latent heat of fusion is L, 1 the rate of increase of the thickness of the ice layer, at this instant would be given by:

1. \(\frac{26 K}{\rho \mathrm{x}(L-4 s)}\)
2. \(\frac{26 K}{\left(\rho x^2 L\right)}\)
3. \(\frac{26 K}{(\rho x L)}\)
4. \(\frac{26 K}{\rho \mathrm{x}(L+4 s)}\)

Answer: 3. \(\frac{26 K}{(\rho x L)}\)

If the area of the cross-section of a surface is not uniform or if the steady state condition is not reached the heat flow equation can be applied to a thin layer of material perpendicular to the direction of heat flow.

The rate of heat flow by conduction for the growth of ice is given by,\(\frac{d \theta}{d t}=\frac{K A\left(\theta_0-\theta_1\right)}{x}\)    → Equation 1

where,\(\mathrm{d} \theta=\rho \mathrm{A} d x L, \theta_0=0 \text { and } \theta_1=-\theta \)

⇒ \(\theta_0=0^{\circ} \mathrm{C} \Rightarrow \theta_1=-26^{\circ} \mathrm{C}\) .

Given that the rate of increase in thickness can be calculated from the equation. (1),

⇒ \(\frac{d \theta}{d t} =\frac{K A\left(\theta_0-\theta_1\right)}{x}\)

⇒ \(\frac{\rho A d x L}{d t} =\frac{K A\left(\theta_0-\theta_1\right)}{x}\)

⇒ \(\frac{d x}{d t} =\frac{K A\left(\theta_0-\theta_1\right)}{\rho A x L}\)

∴ \(\frac{K[0-(-26)]}{\rho x L} =\frac{26 K}{\rho x L}\)

Question 15. Two rods A and B of different materials are welded together as shown in the figure. Their thermal conductivities are K₁ and K₂. The thermal conductivity of the composite rod will be:

1. \(\frac{K_1+K_2}{2}\)
2. \(\frac{3\left(K_1+K_2\right)}{2}\)
3. \(K_1+K_2\)
4. \(2\left(K_1+K_2\right)\)

Answer: 1. \(\frac{K_1+K_2}{2}\)

Heat flow rate, \(H=H_1+H_2\)

H =\(\frac{K_1 A\left(T_1-T_2\right)}{d}+\frac{K_2 A\left(T_1-T_2\right)}{d}\)

⇒ \(\frac{K_{e g}\left(T_1-T_2\right)}{d} =\frac{A\left(T_1-T_2\right)}{d}\left[K_1+K_2\right]\)

∴ \(K_{\text {eg. }} =\left[\frac{K_1+K_2}{2}\right]\)

Question 16. A spherical black body with a radius of 12 cm radiates 450-watt power at 500 J. If the radius were halved and the temperature doubled, the power radiated in watts would be:

1. 225
2. 450
3. 1000
4. 1800

Answer: 4. 1800

From Stefan’s law, Here radiated power of the black body P=\(\sigma \mathrm{AT}^4\) becomes half then a new area

_⇒ \(A^{\prime}=\frac{A}{4}\)

Power radiation, \(\mathrm{P}^{\prime}=\sigma\left(\frac{A}{4}\right)(2 T)^4\)

Question 17. A black body is at a temperature of 5760 K. The energy of radiation emitted by the body at wavelength 250 nm is U₁, at wavelength 500 nm is U₂ and that at 1000 nm is u₃. Wein’s constant, b = 2.88 x 106 nm. Which of the following is correct?

1. U₃ = 0
2. U₁ > U₂
3. U₂ > U₁
4. U₁ = 0

Answer: 3. U₂ > U₁

Temperature, T_\(1=5760 \mathrm{~K}\) (Given)

Using Wien’s law,

⇒ \(\lambda_m T=b\)  →  Equation 1

b= Wien’s constant =\(2.86 \times 10^6 \mathrm{nmK}\)

From (1) \(\lambda_m=\frac{b}{T}\)

⇒ \(\lambda_m=\frac{2.88 \times 10^6 \mathrm{nmK}}{5760 \mathrm{~K}}=500 \mathrm{~nm}\)

∴ \(U_2>U_1\)

Question 18. Two metal rods 1 and 2 of the same length have the same temperature difference between their ends. Their thermal conductivities are K₁ and K₂ and cross-sectional areas A₁ and A₂ respectively. If the rate of heat conduction in 1 is four times that in 2, then:

1. K₁A₁ = 4K₂A₂
2. K₁A₁ = 2K₂A₂
3. 4K₁A₁ = K₂A₂
4. K₁A₁ =  K₂A₂

Answer: 1. K₁A₁ = 4K₂A₂

Let, L= length of each rod Temperature difference = \(\Delta T\)

The rate of flow of rod (1) is,

⇒ \(H_1=\frac{K_1 A_1 \Delta \mathrm{T}}{L}\)

and Rate of flow of rod (2) is, \(H_2=\frac{K_2 A_2 \Delta T}{L}\)

from the equation,  \(H_1 =4 H_2\)

⇒ \(\frac{K_1 A_1 \Delta \mathrm{T}}{L} =4 \frac{K_2 A_2 \Delta T}{L}\)

∴ \(K_1 A_1 =4 K_2 A_2\)

Question 19. If the radius of a star is R and it acts as a black body, what would be the temperature of the star, in which the rate of energy production is Q?

1. \(\frac{Q}{4 \pi R^2 \sigma}\)
2. \(\left(\frac{Q}{4 \pi R^2 \sigma}\right)^{-\frac{1}{2}}\)
3. \(\left(\frac{4 \pi R^2 Q}{\sigma}\right)^{\frac{1}{4}}\)
4. \(\left(\frac{Q}{4 \pi R^2 \sigma}\right)^{\frac{1}{4}}\)

Answer: 4. \(\left(\frac{Q}{4 \pi R^2 \sigma}\right)^{\frac{1}{4}}\)

From Stefan’s law, we can write,

E=\(\sigma T^4\)

and rate of energy production, Q =\(E \times A \)

= \(\sigma \mathrm{T}^4 A =\sigma T^{4 \pi} 4 \pi \mathrm{R}^2\)

T =\(\left(\frac{Q}{4 \pi \mathrm{R}^2 \sigma}\right)^{1 / 4}\)

Question 20. A slab of stone with an area of 0.36 m2 and thickness of 0.1 m is exposed on the lower surface to steam at 100°. A block of ice at 0°C rests on the upper surface of the slab. In one hour 4.8 kg of ice is melted. The thermal conductivity of the slab is:(Given latent heat of fusion of ice = 3.36 x 105 J kg^-1)

1. 1.24 J/m/s/°C
2. 1.29J/m/s/°C
3. 2.05 J/m/s/°C
4. 1.02J/m/s/°C

Answer: 1. 1.24 J/m/s/°C

We know that,

⇒ \(\frac{d Q}{d t} =\frac{K A}{L}\left(T_1-T_2\right)\)

Q =\(\frac{K A}{L}\left(T_1-T_2\right) t\)

Q = \( m L_f\)

⇒ \(\frac{K A}{L}\left(T_1-T_2\right) t =m L_f\)

K =\(\frac{m \mathrm{~L}_f(\mathrm{~L})}{\mathrm{A}\left(\mathrm{T}_1-\mathrm{T}_2\right) t}\)

= \(\frac{4.8 \times 3.36 \times 10^5 \times 0.1}{0.36 \times 100 \times 3600} \mathrm{~J} / \mathrm{m} / \mathrm{S} /{ }^{\circ} \mathrm{C}\)

= \(\frac{4.8 \times 3.36}{0.36 \times 36}=1.24 \mathrm{~J} / \mathrm{m} / \mathrm{S} /{ }^{\circ} \mathrm{C}\)

Question 21. A cylinder metallic rod is in thermal contact with two reservoirs of heat at its two ends and conducts an amount of heat Q in time t. The metallic rod is melted and the material is formed into a rod of half the radius of the original rod. What is the amount of heat conducted by the new rod when placed in thermal contact with the two reservoirs in time ft?

1. \(\frac{Q}{4}\)
2. \(\frac{Q}{16}\)
3. 2Q
4. \(\frac{Q}{2}\)

Answer: 2. \(\frac{Q}{16}\)

We know that, Amount of heat, Q=\(\frac{K A\left(\theta_1-\theta_2\right) t}{t}\)

Where, K= coefficient of thermal conduction

⇒ \(\frac{Q}{t} \propto \frac{A}{l} \propto \frac{r^2}{l}\)  →   Equation 1

As the metallic rod is melted and the material is formed into a rod of half the radius,

⇒ \(V_1 =V_2\)

⇒ \(\pi r_1^2 l_1 =\pi r_2^2 l_2 \)

⇒ \(l_1 =\frac{l_2}{4}\)  →  Equation 2

From eq. (1) and eq. (2),

⇒ \(\frac{Q_1}{Q_2}=\frac{r_1^2}{l_2} \times \frac{l_2}{r_2^2}=\frac{r_1^2}{l_2} \times \frac{4 l_1}{\left(r_2 / 2\right)^2}\)

∴ \(Q_1=16 Q_2 \)

Question 22. The total radiant energy per unit area, normal to the direction of incidence, received at a distance R from the centre of a star radius r, whose outer surface radiates as a black body at a temperature T K is given by:

1. \(\frac{\sigma r^2 T^4}{R^2}\)
2. \(\frac{\sigma r^2 T^4}{4 \pi r^2}\)
3. \(\frac{\sigma r^4 T^4}{r^4}\)
4. \(\frac{4 \pi \sigma r^4 T^4}{R^2}\)

Answer: 1. \(\frac{\sigma r^2 T^4}{R^2}\)

Using Stefan’s law A \(\sigma T^4=4 \pi r^2 \sigma T^4\)

∴ \(T_{\mathrm{K}}=\sigma r^2 T^4 / \mathrm{R}^2\)

Question 23. A black body is at 727°C. It emits energy at a rate which is proportional to:

1. (1000)⁴
2. (1000)²
3. (727)⁴
4. (727)²

Answer: 1. (1000)4

According to Stefan’s law,

Rate of radiated energy, \(E \propto T^4\)

where, T= absolute temperature of a black body.

⇒ \(E \propto(727+273)^4\)

or \(E \propto[1000]^4\)

Question 24. Assuming the sun to have a spherical outer surface of radius r, radiating like a black body at temperature fC, the power received by a unit surface, (normal to the incident rays) at a distance R from the centre of the sun is where σ is the Stefan’s constant:

1. \(\frac{r^2 \sigma(t+273)^4}{4 \pi R^2}\)
2. \(\frac{16 \pi^2 r^2 \sigma t^4}{R^2}\)
3. \(\frac{r^2 \sigma(t+273)^4}{R^2}\)
4. \(\frac{4 \pi r^2 \sigma t^4}{R^2}\)

Answer: 3. \(\frac{r^2 \sigma(t+273)^4}{R^2}\)

Solar constant =\(\frac{\sigma\left(4 \pi r^2\right) T^4}{\left(4 \pi R^2\right)}\)

= \(\frac{\sigma r^2(t+273)^4}{R^2}\)

Question 25. A black body at 1227°C emits radiations with maximum intensity at a wavelength of 5000 A. If the temperature of the body is increased by 1000°C, the maximum intensity will be observed at:

1. 3000 A
2. 4000 A
3. 5000 A
4. 6000 A

Answer: 1. 3000 A

By Wein’s displacement law, \(\lambda_m T \)= Constant

we have, \(\frac{\lambda_{m 1}}{\lambda_{m 2}}=\frac{T_2}{T_1}\)

or \(\lambda_{m 2}=\frac{\lambda_{m 1} \times T_1}{T_2}\)

∴ \(\lambda_{m 2}=\frac{5000 \times 1500}{2500}=3000\) .

Question 26. Which of the following rods, (given radius r and length l) each made of the same material and whose ends are maintained at the same temperature will conduct the most heat?

1. r=\(r_0, l=l_0\)
2. r=\(2 r_0, l=l_0\)
3. r=\(r_0, l=2 l_0\)
4. r=\(2 r_0, l=2 l_0\)

Answer: 2. r=\(2 r_0, l=l_0\)

Heat conducted =\(\frac{K A\left(T_1-T_2\right) t}{l}=\frac{K \pi r^2\left(T_1-T_2\right) t}{l}\)

The rod with a maximum ratio of \(\frac{A}{l}\) will conduct the most.

Here the rod r= \( 2 r_0 and l=l_0 \) will conduct most.

Question 27. If km denotes the wavelength at which the radioactive emission from a black body at a temperature TK is maximum, then:

1. \(\lambda_m \propto T^1\)
2. \(\lambda_m\) is independent of T
3. \(\lambda_m \propto T\)
4. \(\lambda_m \propto T^{-1}\)

Ans wer: 4. \(\lambda_m \propto T^{-1}\)

According to Wein’s displacement law

⇒ \(\lambda_m T\)= constant

∴ \(\lambda_m \propto T^{-1}\)

Question 28. Consider a compound slab consisting of two different materials having equal thickness and thermal conductivities K and 2K, respectively. The equivalent thermal conductivity of the slab is:

1. \(\frac{2}{3} K\)
2. \(\sqrt{2} K\)
3. 3 K
4. \(\frac{2}{3} K\)

Answer: 1. \(\frac{2}{3} K\)

The slabs are in series.

Total resistance, \(\mathrm{R}=\mathrm{R}_1+\mathrm{R}_2\)

⇒ \(\frac{l}{K_{e f f}(A)}=\frac{l}{2 K A}+\frac{l}{K A}\)

∴ \(K_{\text {eff }}=\frac{2}{3} K\)

Question 29. The Wein’s displacement law expresses the relation between:

1. wavelength corresponding to maximum energy and temperature.
2. relation energy and wavelength.
3. temperature and wavelength.
4. colour of light and temperature.

Answer: 1. relation energy and wavelength.

According to Wein’s displacement law, the wavelength corresponding to maximum energy is inversely proportional to the absolute temperature of the body \(\lambda_m \propto \frac{1}{T}\)

∴ \(\lambda_m T=\text { constant }\)

Question 30. Which of the following is best close to an ideal black body?

1. Black lamp.
2. Cavity maintained at a constant temperature.
3. Platinum black.
4. A lamp of charcoal heated to high temperature.

Answer: 2. Cavity maintained at a constant temperature.

A perfect black body absorbs all incident radiation without reflecting or transmitting any of it. A black-light absorbs around 96% of incoming radiation.

In reality, a perfect black body may be achieved via a tiny hole in the wall of a uniformly heated hollow body (as indicated in the image). Any radiation that enters the hollow body through the perforations is reflected several times before being absorbed. This can be aided by painting the inside surface with black, absorbing around 96% of the energy at each reflection. The section of the inner surface opposite the hole is conical to prevent the reflected beam from escaping after one reflection.

Question 31. For a black body at a temperature of 727°C, its radiating power is 60 W and the temperature of the surrounding is 227°C. If the temperature of the black body is changed to 1227°C, then its radiating power will be:

1. 304 W
2. 320 W
3. 240 W
4. 120 W

Answer: 2. 320 W

We can use the formula,

⇒ \(P\left(T_4-T_0{ }^4\right)\)

⇒ \(\frac{P_2}{P_1} =\frac{(1500)^4-(500)^4}{(1000)^4-(500)^4}\)

=\(\frac{500^4\left(3^4-1\right)}{500^4\left(2^4-1\right)}\)

⇒ \(\frac{P_2}{60} =\frac{80}{15}\)

∴ \(P_2 =320 \mathrm{~W}\)

Question 32. A cup of coffee cools from 90°C to 80°C in two minutes, when the room temperature is 20°C. The time taken by a similar cup of coffee to cool from 80°C to 60°C at a room temperature same at 20°C is:

1. \(\frac{13}{10} t\)
2. \(\frac{13}{5} t\)
3. \(\frac{10}{13} t\)
4. \(\frac{5}{13} t\)

Answer: 2. \(\frac{13}{5} t\)

Given, Initial temperature \(\left(\mathrm{T}_{\mathrm{i}}\right)=90^{\circ} \mathrm{C}\)

Final temperature \(\left(T_f\right)=80^{\circ} \mathrm{C}\)

Room temperature \(\left(\mathrm{T}_{\mathrm{o}}\right)=20^{\circ} \mathrm{C}\)

Let the time taken be t minutes

According to Newton’s law of cooling,

Rate of cooling,

⇒ \(\frac{d T}{d t} =K\left[\frac{\mathrm{T}_i+\mathrm{T}_f}{2}-\mathrm{T}_o\right]\)

∴ \(\left(\frac{\mathrm{T}_f-\mathrm{T}_i}{t}\right) =K\left[\frac{90+80}{2}-20\right]=K[65]\)

K =\(\frac{10}{65 t}\)  →  Equation 1

In \(2^{\text {nd }}\)condition,

Initial temperature \(\mathrm{T}_{\mathrm{i}}=80^{\circ} \mathrm{C}\)

Final temperature \(\mathrm{T}_{\mathrm{f}}=60^{\circ} \mathrm{C}\)

Let the time taken be t minutes

Then,\(\frac{(80-60)}{t^{\prime}} =\frac{10}{65 t}\left[\frac{(80+60)}{2}-20\right] \frac{20}{t^{\prime}} 10\)

=\(\frac{10}{65 t}(50)\)  →  Equation 2

From equation (1) and (2),

∴ \(\mathrm{t}^{\prime}=\frac{13}{5} t\)

Question 33. An object kept in a large room having an air temperature of 25° C takes 12 minutes to cool from 80° C to 70° C. The time taken to cool the same object from 70° C to 60° C would be nearly :

1. 10 min
2. 12 min
3. 20 min
4. 15 min

Answer: 4. 15 min

From Newton’s law of cooling the expression for the time taken by a body to cool from \(T_1 \text { to } T_2\) when placed in a medium of temperature to is given by :

⇒ \(\frac{T_1-T_2}{t}=\frac{1}{K}\left(\frac{T_1+T_2}{2}-T_0\right)\)

The first condition, When the object cools from \(80^{\circ} \mathrm{C} to 70^{\circ}\) in 12 minutes then from equation 1

⇒ \(\frac{80-70}{12}=\frac{1}{K}\left(\frac{80+70}{2}-25\right)\)

Since, \(T_0\) = 25°C is given

K = 60  →  Equation  2

Again when the object cools from \(70^{\circ} \mathrm{C} to 60^{\circ} \mathrm{C}\) we have

⇒ \(\frac{70-60}{t} =\frac{1}{K}\left(\frac{70+60}{2}-25\right)\)

=\(\frac{10}{t} =\frac{40}{\mathrm{~K}}\)

⇒ \(\frac{10}{t} =\frac{40}{60}\)  From Equation 2

t =15 min

Question 34. A body cools from a temperature of 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton’s law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be:

1. \(\frac{7}{4} T\)
2. \(\frac{3}{2} T\)
3. \(\frac{4}{3} T\)
4. T

Answer: 2. \(\frac{3}{2} T\)

According to the formula from Newton’s law of cooling

In \(\frac{3 T-T}{2 T^{\prime}-T}=K t\)

In(\(2)=K(10)\)

for the next 10 minutes

In \(\frac{2 \mathrm{~T}-\mathrm{T}}{\mathrm{T}^{\prime}-\mathrm{T}} =\mathrm{K}(10)\)

⇒ \(\frac{2 \mathrm{~T}-\mathrm{T}}{\mathrm{T}^{\prime}-\mathrm{T}}\) =2

∴ \(\mathrm{~T}^{\prime} =\frac{3}{2}\)

Question 35. A certain quantity of water cools from 70°C to 60°C in the first 5 min and to 54°C in the next 5 min. The temperature of the surroundings is:

1. 45°C
2. 20°C
3. 42°C
4. 10°C

Answer: 1. 45°C

The question is based on Newton’s law of cooling According to Wien displacement law,

⇒ \(\frac{\theta_1-\theta_2}{\Delta t}=K\left[\frac{\theta_1+\theta_2}{2}-\theta_0\right]\)

Where, \(\theta_0=q\)

⇒ \(\frac{70-60}{5} =K\left[\frac{70+60}{2}-\theta_0\right] \)

=\(K\left[65-\theta_0\right]\)  →  Equation 1

⇒ \(\frac{60-54}{5} =K\left[\frac{60+54}{2}-\theta_0\right]=\mathrm{K}\left[57-\theta_0\right]\) → Equation 2

From (1) and (2),

⇒ \(\frac{2 \times 5}{6} =\left(\frac{65-\theta_0}{57-\theta_0}\right)\)

⇒ \(\frac{5}{3} =\frac{65-\theta_0}{57-\theta_0}\)

2 \(\theta_0 =90 \)

∴ \(\theta_0 =45^{\circ} \mathrm{C}\) .

Question 36. A piece of iron is heated in a flame. If first becomes dull red then becomes reddish yellow and finally turns to white hot. The correct explanation for the above observation is possible by using:

1. Stefan’s law
2. Wein’s displacement law
3. KirchofFs law
4. Newton’s law of cooling

Answer: 2. Wein’s displacement law

We can explain this observation by using \(\lambda_m T=b\)

Which is Wien’s displacement law

Question 37. The two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperatures T₁ and T2(T₁ > T₂). The rate of heat transfer, through the rod in a steady state is given by:

1. \(\frac{d \mathrm{Q}}{d t}=\frac{K L\left(T_1-T_2\right)}{A}\)
2. \(\frac{d \mathrm{Q}}{d t}=\frac{K\left(T_1-T_2\right)}{L A}\)
3. \(\frac{d \mathrm{Q}}{d t}=K L A\left(T_1-T_2\right)\)
4. \(\frac{d \mathrm{Q}}{d t}=\frac{K A\left(T_1-T_2\right)}{L}\)

Answer: 4. \(\frac{d \mathrm{Q}}{d t}=\frac{K A\left(T_1-T_2\right)}{L}\)

The rate of heat transfer \((\mathrm{dQ} / \mathrm{dt})\) is given by:

For a rod of length land area of cross-section A whose faces are maintained at temperature T₁ and T₂ respectively then in steady-state the rate of heat flowing from one face to the other in time T is given by Here temperature difference \((\Delta \mathrm{T})=\left(\mathrm{T}_1-\mathrm{T}_2\right)\)

The rate of heat transfer (dQ/dt) is given by

Also, \(\frac{d Q}{d t} =\frac{\Delta T}{R}\)

⇒ \(\mathrm{R} =\frac{L}{k A}\)

∴ \(\frac{d \mathrm{Q}}{d t} =\frac{K A\left(T_1-T_2\right)}{L}\)