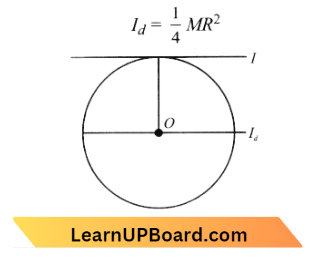
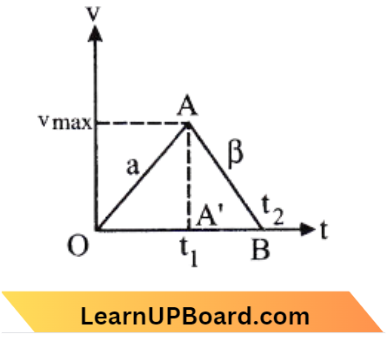
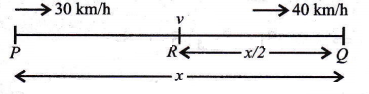
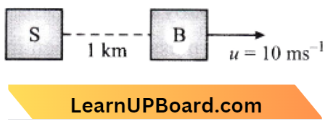
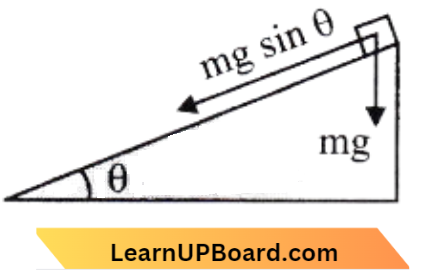
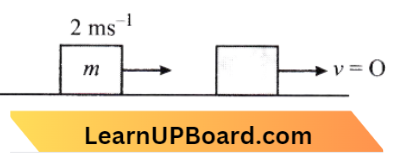
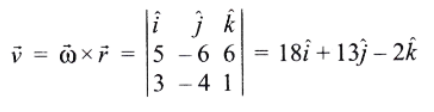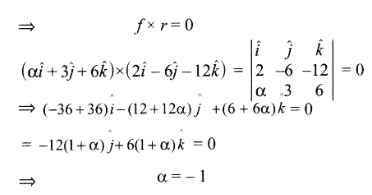NEET Physics For Work, Energy And Power Multiple Choice Questions
Question 1. A particle moves so that its position vector is given by \(\vec{r}=\cos \omega t \hat{x}+\sin \omega t \hat{y}\) where to is a constant. Which of the following is true?
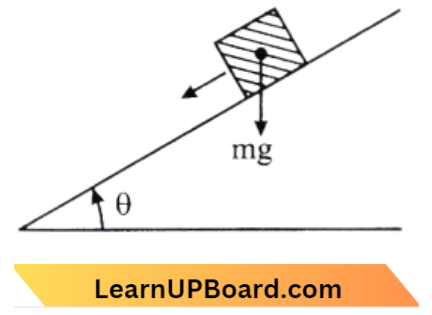
- Velocity is perpendicular to \(\vec{r}\) and acceleration is directed towards the origin.
- Velocity is perpendicular to \(\vec{r}\) and acceleration is directed away from the origin.
- Velocity and acceleration both are perpendicular to \(\vec{r}\).
- Velocity and acceleration both are perpendicular to \(\vec{r}\).
Answer: 2. Velocity is perpendicular to \(\vec{r}\) and acceleration is directed away from the origin.
Given,\(\vec{r}= \cos \omega t \hat{x}+\sin \omega t \hat{y}\)
∴ \(\vec{v} =\frac{d \vec{r}}{d t}=-\omega \sin \omega t \hat{x}+\omega \cos \omega t \hat{y}\)
⇒ \(\vec{a} =\frac{d \vec{v}}{d t}=-\omega^2 \cos \omega t \hat{x}-\omega^2 \sin \omega t \hat{y}=-\omega^2 \vec{r}\)
Since position vector \((\vec{r})\) is directed away from the origin, so, acceleration \(\left(-\omega^2 \vec{r}\right)\) is directed towards the origin.
Also, \(vec{r} . \vec{v}=(\cos \omega t \hat{x}+\sin \omega t \hat{y}) .(-\omega \sin \omega t \hat{x}+\omega \cos \omega t \hat{y})\)
=\(-\omega \sin \omega t \cos \omega t+\omega \sin \omega t \cos \omega t=0\)
∴ \(\vec{r} \perp \vec{v}\)
Question 2. If vectors \(\vec{A}=\cos \omega t \hat{i}+\sin \omega t \hat{j} \text { and } \vec{B}=\cos \frac{\omega t}{2} \hat{i}+\sin \frac{\omega t}{2} \hat{j}\) are functions of time, then the value of t at which they are orthogonal to each other is:
- \(\mathrm{t}=\frac{\pi}{\omega}\)
- t=0
- t=\(\frac{\pi}{4 \omega}\)
- \(\mathrm{t}=\frac{\pi}{2 \omega}\)
Answer: 1. \(\mathrm{t}=\frac{\pi}{\omega}\)
Given
If vectors \(\vec{A}=\cos \omega t \hat{i}+\sin \omega t \hat{j} \text { and } \vec{B}=\cos \frac{\omega t}{2} \hat{i}+\sin \frac{\omega t}{2} \hat{j}\) are functions of time
Two vectors\(\vec{A} \text { and } \vec{B}\) are orthogonal to each other, if their scalar product is zero i.e. \(\vec{A} \cdot \vec{B}=0\)
Here, \(\vec{A}=\cos \omega \mathrm{t} \vec{i}+\sin \omega \mathrm{t} \vec{j}\)
and \(\vec{B}=\cos \frac{\omega t}{2} \hat{i}+\sin \frac{\omega t}{2} \hat{j}\)
⇒ \(\vec{A} \cdot \vec{B} =(\cos \omega t \hat{i}+\sin \omega t \hat{j}) \cdot\left(\cos \frac{\omega t}{2} \hat{i}+\sin \frac{\omega t}{2} \hat{j}\right)\)
=\(\cos \omega t \cos \frac{\omega t}{2}+\sin \omega t \sin \frac{\omega t}{2} \cos\)
=\(\cos \left(\omega t-\frac{\omega t}{2}\right)\)
Read and Learn More NEET Physics MCQs
But \(\vec{A} \cdot \vec{B}=0\) as \(\vec{A}\) and \(\vec{B}\) are orthogonal to each other
⇒ \(\cos \left(\omega t-\frac{\omega t}{2}\right)\)=0
⇒ \(\left(\omega t-\frac{\omega t}{2}\right)=\cos \frac{\pi}{2}\)
{ or } \(\omega t-\frac{\omega t}{2}=\frac{\pi}{2}\)
⇒ \(\frac{\omega t}{2}=\frac{\pi}{2}\)
∴ \(\text { or } \quad t=\frac{\pi}{\omega}\)
Question 3. If a vector \(2 \hat{i}+3 \hat{j}+8 \widehat{k}\) is perpendicular to the vector \(4 \hat{j}-4 \hat{i}+\alpha \hat{k}\) , then the value of a is:
- 1/2
- -1/2
- 1
- -1
Answer: 2. -1/2
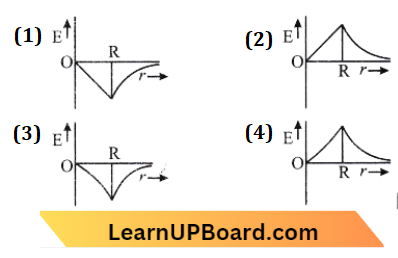
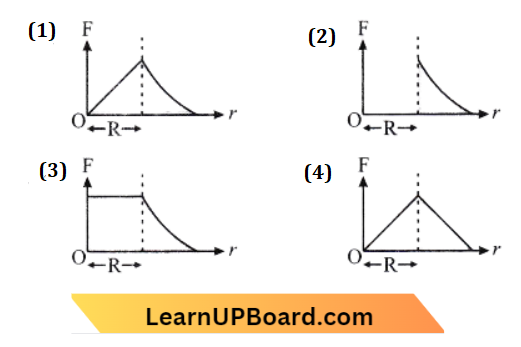
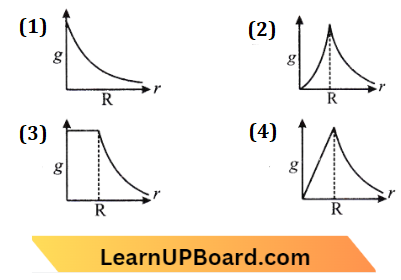
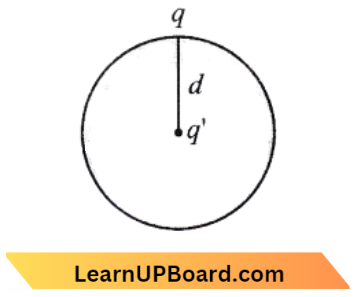
⇒ \(\vec{a}=2 \hat{i}+3 \hat{j}+8 \hat{k}, \hat{b}=4 \hat{j}-4 \hat{i}+\alpha \hat{k}\)
⇒ \(\vec{a} \cdot \vec{b}=0 \text { if } \vec{a} \perp \vec{b}\)
⇒ \((2 \hat{i}+3 \hat{j}+8 \hat{k}) \cdot(-4 \hat{i}+4 \hat{j}+\alpha \hat{k})\)=0
⇒ \(\text { or, }-8+12+8 \alpha\)=0
⇒ \(4+8 \alpha=0 \)
∴ \(\alpha=-1 / 2\)
Question 4. The vector sum of two forces is perpendicular to their vector differences. In that case, the forces:
- are equal to each other
- are equal to each other in magnitude
- are not equal to each other in magnitude
- cannot be predicted.
Answer: 2. are equal to each other in magnitude
Given \(\left(\vec{F}_1+\vec{F}_2\right) \perp\left(\vec{F}_1-\vec{F}_2\right)\)
⇒ \(\left(\vec{F}_1+\vec{F}_2\right) \cdot\left(\vec{F}_1-\vec{F}_2\right)\)=0
⇒ \(F_1^2-F_2^2-\vec{F}_1 \cdot \vec{F}_2+\vec{F}_2 \vec{F}_1\)=0
⇒ \(F_1^2=F_2^2\)
∴ F1, F2 are equal to each other in magnitude
Question 5. The position vector of a particle is \(\vec{r}=(a \cos \omega t) \hat{i}-(a \sin \omega t) \hat{j}\) . The velocity of the particle is:
- directed towards the origin
- directed away from the origin
- parallel to the position vector
- perpendicular to the position vector.
Answer: 2. directed away from origin
Position vector of the particle,
⇒ \(\vec{r}=(\mathrm{a} \cos \omega t) \vec{i}+(\mathrm{a} \sin \omega t) \vec{j}\)
velocity vector \(\vec{v}=\frac{d \vec{r}}{d t}=(-\mathrm{a} \omega \sin \omega t) \hat{i}+(\mathrm{a} \omega \cos \omega t) \hat{j}\)
=\(\omega[(-\mathrm{a} \sin \omega t) \hat{i}+(\mathrm{a} \cos \omega t) \hat{j}]\)
⇒ \(\vec{v} \cdot \vec{r}=\omega a[-\sin \omega t \hat{i}+\cos \omega t \hat{j}] \cdot[\mathrm{a} \cos \omega t \vec{i}+\mathrm{a} \sin \omega t \hat{j}]\)
=\(\omega\left[-\mathrm{a}^2 \sin \omega t \cos \omega t+a^2 \cos \omega t \sin \omega t\right]\)=0
Therefore velocity vector is perpendicular to the position vector.
Question 6. The angle between the two vectors \(\vec{A}=3 \hat{i}+4 \hat{j}+5 \hat{k}\) and \(\vec{B}=3 \hat{i}+4 \hat{j}-5 \hat{k}\) will be:
- 90°
- 180°
- zero
- 45°
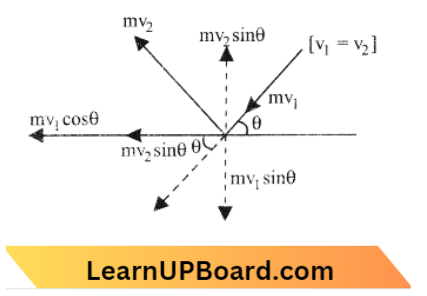
Answer: 1. 90°
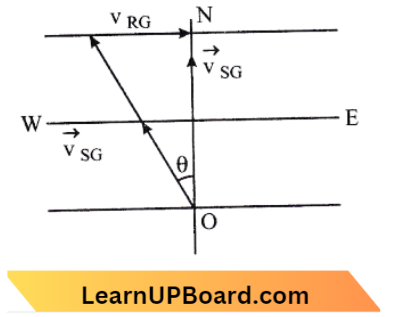
⇒ \(\vec{A}=3 \hat{i}+4 \hat{j}+5 \hat{k} \text { and } \hat{B}=3 \hat{i}+4 \hat{j}-5 \hat{k}\)
⇒ \(\cos \theta=\frac{\vec{A} \cdot \vec{B}}{|\vec{A}||\vec{B}|}\)
=\(\frac{(3 \hat{i}+4 \hat{j}+5 \hat{k}) \cdot(3 \hat{i}+4 \hat{j}-5 \hat{k})}{\left[\sqrt{(3)^2+(4)^2+(5)^2}\right]}\)\(\times\left[\sqrt{(3)^2+(4)^2+(5)^2}\right]\)
=\(\frac{9+16-25}{50}=0 \text { or } \theta=90^{\circ}\)
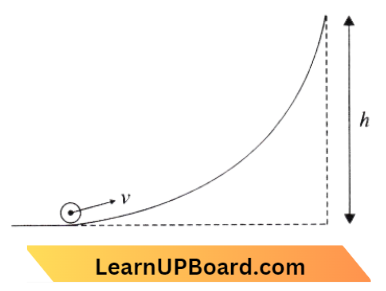
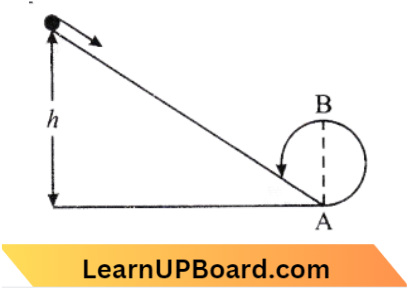
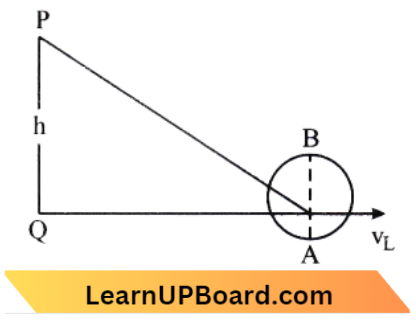
Question 7. Consider a drop of rainwater having a mass of 1 g falling from a height of 1 km. It hits the ground with a speed of 50 m/s. Take g, constant with a value of 10 m/s². The work done by the [1] gravitational force and the [2] resistive force of air is:
- (1) – 10J, (2) – 8.25 J
- (1) – 1.25J, (2) – 8.25 J
- (1) – 100J, (2) – 8.75 J
- (1) – 10J, (2) – 8.75 J
Answer: 4. (1) – 10J, (2) – 8.75 J
Given
Consider a drop of rainwater having a mass of 1 g falling from a height of 1 km. It hits the ground with a speed of 50 m/s. Take g, constant with a value of 10 m/s².
Work done by gravitational force, W = mgh
W= 10-3x 10 x 1 x 103= [10]
From the work-energy theorem,
Work done = change in KE
⇒ \(\Delta K=W_{\text {gravity }}+W_{\text {air resistance }}\)
⇒ \(\frac{1}{2}=m g h+W_{\text {air resist }}\)
⇒ \(W_{\text {air resist }}=\frac{1}{2}-m g h=10^{-3}\)
= \(10^{-3}\left(\frac{1}{2} \times 50 \times 50-10 \times 10^3\right)\)
= -8.75J
Question 8. A particle of mass l0g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration if the kinetic energy of the particle becomes equal to 8 x 10-4 by the end of the second revolution after the beginning of the motion?
- 0.18 m/s²
- 0.2 m/s²
- 0.1 m/s²
- 0.15 m/s²
Answer: 3. 0.1 m/s²
Given
A particle of mass l0g moves along a circle of radius 6.4 cm with a constant tangential acceleration.
Here, m = 10 g = 10-2 kg, R = 6.4 cm = 6.4 x 10-2 m,
Kf = 8 x 10-4 J, K, = 0, a, = 7
Using the work-energy theorem, Work done by all the forces = Change in KE
⇒ \(\mathrm{W}_{\text {tangential force }}+\mathrm{W}_{\text {centripetal force }}=\mathrm{K}_f-\mathrm{K}_i\)
⇒ \(a_t=\frac{K_f}{4 \pi R m}\)
=\(\frac{8 \times 10^{-4}}{4 \times \frac{22}{7} \times 6.4 \times 10^{-2} \times 10^{-2}}\)
=\(0.099=0.1 \mathrm{~m} \mathrm{~s}^{-2}\)
Question 9. A bullet of mass 10 g leaves a rifle at an initial velocity of 1000 m/s and strikes the earth at the same level with a velocity of 500 m/s. The work done in joule to overcome the resistance of air will be:
- 375
- 3750
- 5000
- 500
Answer: 2. 3750
Given
A bullet of mass 10 g leaves a rifle at an initial velocity of 1000 m/s and strikes the earth at the same level with a velocity of 500 m/s.
According to the work-energy theorem, work done by a force in displacing a body determines the change in kinetic energy of the body or W=\(\Delta K E\)
= final \(\mathrm{KE}-\text { initial } \mathrm{KE}\)
=\(\frac{1}{2} m v^2-\frac{1}{2} m u^2\)
Given, v=1000\(\mathrm{~m} / \mathrm{s}, m=10 \mathrm{~g}\)
Putting the values of \(m_1, u_1\) and \(v_1,\) we get
⇒ \(\quad W =\frac{1}{2} \times 0.01\left[(1000)^2-(500)^2\right]\)
=\(3750 \mathrm{~J}\)
Question 10. A force F = 20 + 10y acts on a particle in y-direction, where F is in Newton and y in meter. Work done by this force to move the particle from y = 0 to y = 1 m is :
- 5 J
- 25 J
- 20 J
- 30 J
Answer: 2. 25 J
Work done by the variable force is,
⇒ \(\mathrm{W}=\int_{y_i}^{y_f} \mathrm{~F} d y\)
Here, \(y_i=0 and y_f=1 \mathrm{~m}\)
⇒ \(W =\int_{y_i}^{y_f}(20+10 y) d y\)
=\(\left[20 y+\frac{10 y^2}{2}\right]_0^1=25 \mathrm{~J}\)
Question 11. The work done to raise a mass m from the surface of the earth to a height h, which is equal to the radius of the earth, is:
- 2mgR
- \(\frac{1}{2}\) mgR
- \(\frac{3}{2}\)mgR
- mgR
Answer: 2. \(\frac{1}{2}\) mgR
The initial potential energy at the earth’s surface is,
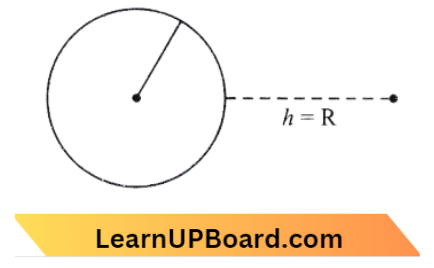
⇒ \(U_i=-\frac{G M m}{R}\)
The final potential energy at height, h =R
⇒ \(U_f =-\frac{G M m}{2 R}\)
From the work-energy theorem,
Work done \(=\text { Change in } \mathrm{KE}\)
W=\(U_f-V_i\)
=\(\frac{G u m}{2 R}=\frac{g R^2 m}{2 R}\)
=\(\frac{m g R}{2}\)
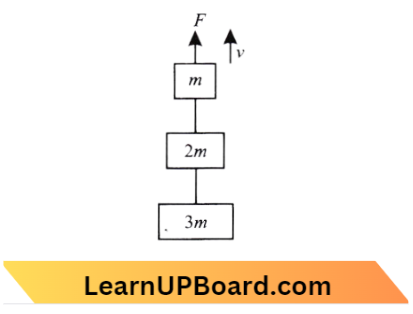
Question 12. A disc of radius 2 m and mass 100 kg rolls on a horizontal floor. Its center of mass has a speed of 20 cm/s. How much work is needed to stop it?
- 33 kJ
- 2 J
- 1 J
- 3 J
Answer: 4. 3 J
We know that, Work required = Change in kinetic energy
So, \(\mathrm{K}. \mathrm{E}=\frac{1}{2} m v^2+\frac{1}{2} \mathrm{I} \omega^2\)
=\(\frac{3}{4} m v^2\)
=\(\frac{3}{4} \times 100 \times\left(20 \times 10^{-2}\right)^2\)
∴ \(\Delta \mathrm{KE} =3 \mathrm{~J}\)
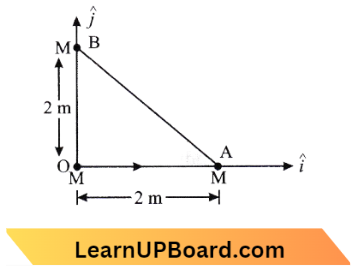
Question 13. A particle moves from a point \((-2 \hat{i}+5 \hat{j}) \text { to }(4 \hat{j}+3 \hat{k})\) when a force of \((4 \hat{i}+3 \hat{j}) \mathrm{N}\) is applied. How much work has been done by the force?
- 8 J
- 11 J
- 5 J
- 2 J
Answer: 3. 5 J
Here \(\vec{F}=(-2 \hat{i}+5 \hat{j}) \mathrm{m}\)
⇒ \(\vec{r}=(4 \hat{j}+3 \hat{k}) \mathrm{m}\)
⇒ \(\vec{F}=(4 \hat{i}+3 \hat{j}) \mathrm{N}, \mathrm{W}\)=?
Work done by force in moving from \(\overrightarrow{r_1}\) to \(\overrightarrow{r_1}\)
⇒ \(\mathrm{W} =\vec{F} \cdot\left(\overrightarrow{r_2}-\overrightarrow{r_1}\right)\)
⇒ \(\mathrm{W} =(4 \hat{i}+3 \hat{j}) \cdot(4 \hat{j}+3 \hat{k}+2 \hat{i}-5 \hat{j})\)
= \((4 \hat{i}+3 \hat{j}) \cdot(2 \hat{i}-\hat{j}+3 \hat{k})\)
= \(8+(-3)=5 \mathrm{~J}\)
Question 14. A uniform force of \((3 \hat{i}+\hat{j})\) N acts on a particle of mass 2 kg. Hence the particle is displaced from position \((2 \hat{i}+\hat{k})\) m to position \((4 \hat{i}+3 \hat{j}-\hat{k})\) m. The work done by the force on the particle is:
- 9 J
- 6 J
- 13 J
- 15 J
Answer: 1. 9 J
Work done = F.S
From the question, \(F=(3 \hat{i}+\hat{j}) N\)
⇒ \(\mathrm{~S}=r_2-r_1\)
⇒ \(\left\{r_1\right.=2 \hat{i}+\hat{k} ; r_2=4 \hat{i}+3 \hat{j}-\hat{k}\)
= \(4 \hat{i}+3 \hat{j}-\hat{k}-(2 \hat{i}+\hat{k})\)
= \((2 \hat{i}+3 \hat{j}-2 \hat{k}) m\)
⇒ \(\mathrm{~W}=\mathrm{F} . \mathrm{S} .=(3 \hat{i}+\hat{j})(2 \hat{i}+3 \hat{j}-2 \hat{k})\)
⇒ \(3 \times 2+3+0=09\)
⇒ \(\{\hat{i} . \hat{i}=1 \hat{i} \cdot \hat{j}=0\} \mathrm{J} \hat{j} \cdot \hat{j}=1 \hat{j} \cdot \hat{k}\)=0
∴ \(\hat{k} \cdot \hat{k}=1 \hat{k} \cdot \hat{i}=0\}\)
Question 15. A body of mass 10 kg is released from a wall of height 20 m and acquires a velocity of 10 ms-1 after falling through the distance 20 m then the work done by the push of the air on the body is:
- 1456 J
- 1500 J
- -1500 J
- -1456 J
Answer: 3. -1500 J
From the Work Energy Theorem, Work done = change in K.E.
⇒ \(W_{\text {gravity }}+W_{\text {air }}\) =K E
⇒ \(m g h +W_{\text {air }}=\frac{1}{2} m v^2-\frac{1}{2} m u^2\)
Putting the values in the above equation, \(10 \times 10 \times 20+W_{\text {air }} =\frac{1}{2}(10)(10)^2-0\)
∴ \(W_{\text {air }}=-1500 \mathrm{~J}\)
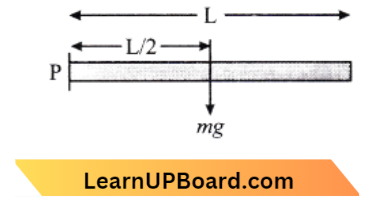
Question 16. A chain of mass m and length L is placed, on a table in such a way that its \(\frac{1}{n}\) the part is hanging below the edge of
- \(\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)
- \(\frac{\mathrm{MgL}}{\mathrm{n}^2}\)
- \(\frac{\mathrm{MgL}}{2 \mathrm{n}}\)
- \(\frac{\mathrm{MgL}}{\mathrm{n}}\)
Answer: 1. \(\frac{\mathrm{MgL}}{2 \mathrm{n}^2}\)
The potential energy of chain at table level, \(U_f =0 \text { and } v_i=-m g h\)
⇒ \(v_i =-\left(\frac{\mathrm{M}}{\mathrm{L}}\right)\left(\frac{\mathrm{L}}{n} g\right)\left(\frac{\mathrm{L}}{2 n}\right)=-\frac{\mathrm{MgL}}{2 n^2}\)
⇒ \(\text { Work done } =v_f-v_i\)
=\(\left[-\frac{M g L}{2 n^2}\right]=\frac{M g L}{2 n^2}\)
Question 17. A body moves a distance of 10 m in a straight line under the action of a 5 N force. If the work done is 25 J, then the angle between the force and direction of motion of the body is:
- 60°
- 75°
- 30°
- 45°
Answer: 1. 60°
Distance(s) = 10 m;
Force(F)=5N
and work done (W) = 25 J Work done (W) = Fs cosθ
25 = 5 x 10 cosθ = 50 cosθ or cos θ = 25/50 = 0.5 or θ = 60°
Question 18. A body, constrained to move in the y-direction, is subjected to a force given by F=\((-2 \hat{i}+15 \hat{j}+6 \hat{k})\) N. The work done by this force in moving the body through a distance of 10 \(\hat{j}\) m along the y-axis, is:
- 150 J
- 20 J
- 190 J
- 160 J
Answer: 1. 150 J
Force \(\vec{F}=(-2 \hat{i}+15 \hat{j}+6 \hat{k}) \mathrm{N}\), and distance, \(\mathrm{d}=10 \vec{j} \mathrm{~m}\)
Work done \(\mathrm{W} =\vec{F} \vec{d}=(-2 \hat{i}+15 \hat{j}+6 \hat{k}) \cdot(10 \hat{j})\)
=\(150 \mathrm{Nm}=150 \mathrm{~J}\)
Question 19. When a body moves with a constant speed along a circle:
- no work is done on it
- no acceleration is produced in it
- its velocity remains constant
- no force acts on it.
Answer: 1. no work is done on it
Question 20. A particle is released from height S from the surface of the Earth. At a certain height, its kinetic energy is three times its potential energy. The light from the surface of the earth and the speed of the period. At that instant are respectively:
- \(\frac{\mathrm{S}}{4}, \frac{3 g \mathrm{~S}}{2}\)
- \(\frac{\mathrm{S}}{4}, \frac{\sqrt{3 g S}}{2}\)
- \(\frac{\mathrm{S}}{2}, \frac{\sqrt{3 g \mathrm{~S}}}{2}\)
- \(\frac{\mathrm{S}}{4}, \frac{\sqrt{3 g S}}{2}\)
Answer: 2. \(\frac{\mathrm{S}}{4}, \frac{\sqrt{3 g S}}{2}\)
Given, Height=S
Arbitrary hieight=h
where KEh=3 PEh
h=? vh=?
At the height ‘h’, TE = mg S
At arbitrary height ‘h’, (h< S)
PE= mgh
⇒ \(\mathrm{KE} =\frac{1}{2} \mathrm{mv}^2\)
⇒ \(\mathrm{v}^2=2 \mathrm{~g}(\mathrm{~S}-h)\)
Where \(\mathrm{v}^2=2 \mathrm{~g}(\mathrm{~S}-h)\)
⇒ \(\mathrm{KE}=\frac{1}{2} \mathrm{mv}^2\)
⇒ \(\mathrm{v}^2 =2 \mathrm{~g}(\mathrm{~S}-h)\)
⇒ \(\mathrm{KE} =\frac{1}{2} m 2 g(\mathrm{~S}-h)\)
= \(m g(\mathrm{~S}-h)\)
Given,\(\mathrm{KE}_n =3 \mathrm{PE}_n\)
⇒ \((\mathrm{~S}-h) =3 m g h\)
⇒ \(\mathrm{~S}-h =3 h\)
⇒ \(\mathrm{~S} =4 h\)
∴ h =\(\frac{\mathrm{S}}{4}\)
∴ \(v^2 =2 g\left(\mathrm{~S}-\frac{\mathrm{S}}{4}\right)\)
⇒ \(v^2 =2 g \frac{3 \mathrm{~S}}{4}\)
∴ \(v =\sqrt{\frac{3 g s}{2}}\)
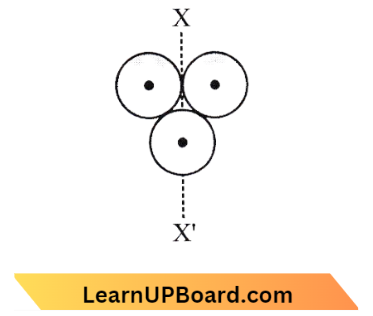
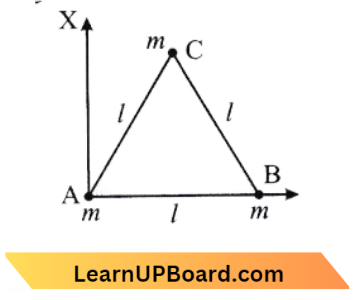
Question 21. A particle of mass 5 m at rest suddenly breaks on its own into three fragments. Two fragments of mass m each move along mutually perpendicular directions with each speed v. The energy released during the process is:
- \(\frac{3}{5} m v^2\)
- \(\frac{5}{3} m v^2\)
- \(\frac{3}{2} m v^2\)
- \(\frac{4}{3} m v^2\)
Answer: 4. \(\frac{4}{3} m v^2\)
From the law of conservation of linear moments,
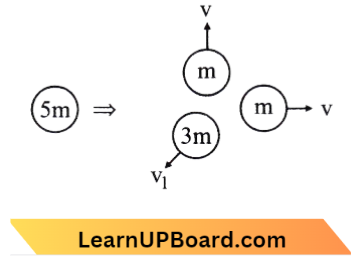
0 =\(m v \hat{j}+m v \hat{i}+3 m \vec{v}_{\mathrm{t}}\)
⇒ \(\vec{v}_1 =\frac{v}{3}(\hat{i}+\hat{j})\)
⇒ \(v_1 =\frac{\sqrt{2}}{3} v\)
\(\mathrm{KE}_i\)=0
⇒ \(\mathrm{KE}_f =\frac{1}{2}+\frac{1}{2}+\frac{1}{2}(3 \mathrm{~m})\left(\frac{\sqrt{2}}{3}\right)^2 v^2\)
=\(m v^2+\frac{m v^2}{3}=\frac{4}{3} m v^2 \)
∴ \(\Delta \mathrm{KE} =\mathrm{KE}_f-\mathrm{KE}_i=\frac{4}{3} m v^2\)
Question 22. A block of mass 10 kg moving in the x-direction with a constant speed of 10 ms-1, is subjected to a retarding force F = 0.1 x J/m during its travel from x = 20 m to 30 m. Its final KE will be:
- 475 J
- 450 J
- 275 J
- 250 J
Answer: 1. 475 J
According to the question, Mass of the block, m = 10 kg
Speed of block, V = 10 ms-1
Retarding force, f = 0.1 J/m
Using the work-energy theorem, Work done = change in kinetic energy
⇒ \(W =K E_f-K E_i\)
⇒ \(K E_f =W+K E_i\)
=\(\int_{20}^{30}-0.1 \times x d x+\frac{1}{2} \times 10 \times 10^2\)
=\(\left[-0.1 \frac{x^2}{2}\right]_{20}^{30}+500\)
=\(-0.1 \times \frac{500}{2}+500\)
=\(-25+500=475 \mathrm{~J}\)
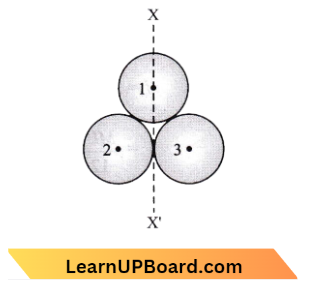
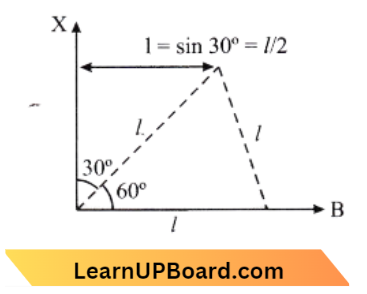
Question 23. A body of mass (4 m) is lying in the XY plane at rest. It explodes into three pieces. Two pieces each of mass (m) move perpendicular to each other with equal speeds (v). The total kinetic energy generated due to the explosion is:
- \(m v^2\)
- \(\frac{3}{2} m v^2\)
- \(2 m v^2\)
- \(4 m v^2\)
Answer: 2. \(\frac{3}{2} m v^2\)
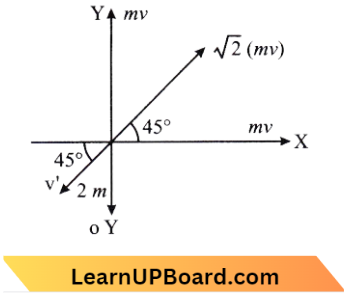
⇒ \(\sqrt{2} m v\)= Resultant momentum of two small mass masses
Using law of conversation of momentum \(\sqrt{2} =2 m v^{\prime}\)
⇒ \(v^{\prime} =\frac{1}{\sqrt{2} m}\)
Now total kinetic energy by the explosion is \(\mathrm{k}=\frac{1}{2} m v^2+\frac{1}{2} m v^2+\frac{1}{2}(2 \mathrm{~m}) v^{\prime 2}\)
= \(m v^2+m\left(\frac{\mathrm{v}}{\sqrt{2}}\right)^2=m v^2+\frac{m v^2}{2}\)
= \(\frac{3}{2} m v^2\)
Question 24. An engine pumps water continuously through a hose. Water leaves the hose with a velocity v and m is the mass per unit length of the water jet. What is the rate at which kinetic energy is imparted to water?
- \(\frac{1}{2} m v^3\)
- \(m v^2\)
- \(\frac{1}{2} m v^2\)
- \(\frac{1}{2} m^2 v^2\)
Answer: 1. \(\frac{1}{2} m v^3\)
Let m = mass per unit length
Rate of mass per sec =\(\frac{m x}{t}\)
=\(m \frac{x}{t}=m v\)
Rate Of KE =\(\frac{1}{2}(m v) V^2\)
=\(\frac{1}{2} m v^3\)
Question 25. A bomb of mass 30 kg at rest explodes into two pieces of masses 18 kg and 12 kg. The velocity of 18 kg mass is 6 ms-1. The kinetic energy of the other mass is:
- 324 J
- 486 J
- 256 J
- 524 J
Answer: 2. 486 J
According to the law conservation of angular momentum
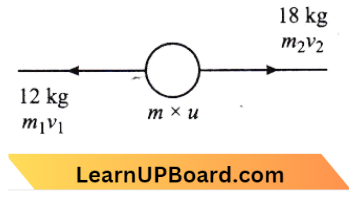
30 x 0 = 18 x 6 + 12 x v
v = – 9 m/s
The negative sign indicates that both fragments move in opposite directions.
⇒ \(\text { K.E. of } 12 \mathrm{~kg} =\frac{1}{2} \mathrm{~m} v^2\)
=\(\frac{1}{2} \times 12 \times 81\)
=\(486 \mathrm{~J}\)
Question 26. A ball of mass 2 kg and another of mass 4 kg are dropped together from a 60-foot-tall building. After a fall of 30 feet each toward Earth, their respective kinetic energies will be in the ratio of:
- \(\sqrt{2}+1\)
- 1:4
- 1:2
- \(1:\sqrt{2}\)
Answer: 3.
Let E1 and E2 be the K.E. of two bodies.
Then, \(E_1=\frac{1}{2} m_1 v_1^2\)
⇒ \(E_2=\frac{1}{2} m_2 v_2^2\)
⇒ \(\frac{E_1}{E_2}=\frac{\frac{1}{2} m_1 v_1^2}{\frac{1}{2} m_2 v^2}=\frac{m_1 v_1^2}{m_2 v_2^2}\)
The initial velocity of both bodies is zero. v²= 2gh is the same for both bodies
∴ \(\frac{E_1}{E_2}=\frac{m_1}{m_2}=\frac{2}{4}=\frac{1}{2}\)
Question 27. A particle of mass m1 is moving with a velocity vj and another particle of mass m2 is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If m1 > m2 then:
- \(E_1<E_2\)
- \(\frac{E_1}{E_2}=\frac{m_1}{m_1}\)
- \(E_1>E_2\)
- \(E_1=E_2\)
Answer: 1. \(E_1<E_2\)
We know that, K.E = \(\frac{p^2}{2 m}\)
⇒ \(\text { K.E. }=\frac{p^2}{2 m}\)
⇒ \(\frac{E_1}{E_2}=\frac{p_1^2 / 2 m_1}{p_2^2 / 2 m_2}\)
⇒ \(\frac{E_1}{E_2}=\frac{m_2}{m_1}\)
Here, \(m_1=m_2\)
∴ \(E_1<E_2\)
Question 28. A stationary particle explodes into two particles of masses m1 and m2 which are in opposite directions with velocities v1 and v2. The ratio of their kinetic energies E1/ E2 is:
- \(\frac{m_2}{m_1}\)
- \(\frac{m_1}{m_2}\)
- 1
- \(\frac{m_1+m_2}{m_2 m_1}\)
Answer: 1. \(\frac{m_2}{m_1}\)
According to the law of conservation of linear momentum, \(m_1 v_1 =m_2 v_2\)
⇒ \(E_1=\frac{1}{2} m_1 v_1^2, E_2 =\frac{1}{2} m_2 v_2^2\)
⇒ \(\frac{E_1}{E_2}=\frac{\frac{1}{2} m_1 v_1^2}{\frac{1}{2} m_2 v_1^2} =\frac{\left(m_1 v_1\right)^2}{\left(m_2 v_2\right)^2} \times \frac{m_2}{m_1}\)
∴ \(\frac{E_1}{E_2} =\frac{m_2}{m_1}\)
Question 29. If the kinetic energy of a body is increased by 300%, then the percentage change in momentum will be:
- 100%
- 150%
- 265%
- 73.2%
Answer: 1. 100%
Here, \(p_1=\sqrt{2 m E_1} and p_2=\sqrt{2 m E_2}\)
⇒ \(p^{\prime} =\sqrt{2 m\left(E+\frac{300}{100} E_1\right)}\)
=\(\sqrt{2 m 4 E_1}\)
=\(2 n_1\)
So, the momentum will change by 100%
Question 30. A particle is projected making an angle of 45° with horizontal having kinetic energy K. The kinetic energy at the highest point will be:
- \(\frac{K}{\sqrt{2}}\)
- \(\frac{K}{2}\)
- \(2 \mathrm{~K}\)
- \(\mathrm{K}\)
Answer: 2. \(\frac{K}{2}\)
Kinetic energy of ball = K and angle of projection (9) = 45°
The velocity of the ball at the highest point = v cos θ
⇒ \(v \cos 45^{\circ}=\frac{v}{\sqrt{2}}\)
Therefore the kinetic energy of the ball \(\frac{1}{2} \mathrm{mx}\left(\frac{v}{\sqrt{2}}\right)^2=\frac{1}{4} \mathrm{mv}^2=\frac{k}{2}\)
Question 31. If the momentum of a body is increased by 50%, then the percentage increase in its kinetic energy is:
- 50%
- 100%
- 125%
- 200%
Answer: 3. 125%
Let p1, and p2 be the initial momentum and inversed momentum respectively
⇒ \(So, p_2 =\frac{150}{100} p_1\)
⇒ \(m v_2 =\frac{15}{10} m v_1\)
⇒ \(m v_2=\frac{15}{10} m v_1\)
⇒ \(\left(p_1=m v_1, p_2=m v_2\right)\) or
⇒ \(v_2=\frac{15}{10} v_1\)
Now \(,\frac{E_2}{E_1} =\frac{\frac{1}{2} m v_2^2}{\frac{1}{2} m v_1^2}=\left(\frac{v_2}{v_1}\right)^2\)
=\(\left(\frac{15}{10}\right)^2=\frac{225}{100}\)
⇒ Clearly, \(\quad E_2>E_1\)
So, percentage increase in K.E. =\(\frac{\left(E_2-E_1\right)}{E_1} \times 100\)
=\(\left(\frac{225}{100}-1\right) \times 100=125 \%\)
Question 32. The kinetic energy acquired by a mass m in traveling distance d, starting from rest, under the action of a constant force is directly proportional to:
- \(\mathrm{m}\)
- \(\mathrm{m}^0\)
- \(\sqrt{m}\)
- \(1 / \sqrt{m}\)
Answer: 2. \(\mathrm{m}^0\)
⇒ \(v^2=u^2+2 a s \text { or } v^2-u^2=2 a s\) or
⇒ \(v^2-(0)^2=2 \times \frac{F}{m} \times \mathrm{s} \text { or } v^2=\frac{2 F s}{m}\)
⇒ \(\text { K.E. }=\frac{1}{2} m v^2=\frac{1}{2} m \times \frac{2 F s}{m}=\text { Fs. }\) and
∴ Thus K.E. is independent of m or directly proportional to\( \mathrm{m}^0\).
Question 33. Two masses of 1 g and 9 g are moving with equal kinetic energies. The ratio of the magnitudes of their respective linear momenta is:
- 1: 9
- 9: 1
- 1 :3
- 3: 1
Answer: 3. 1 :3
⇒ \(\frac{K_1}{K_2}=\frac{p_1^2}{p_2^2} \times \frac{M_1^2}{M_2^2}\)
⇒ \(\text { Here } \quad \mathrm{K}_1=\mathrm{K}_2\)
⇒ \(\frac{p_1}{p_2}=\sqrt{\frac{M_1}{M_2}}=\sqrt{\frac{1}{9}}=\frac{1}{3}\)
or,\(P_1: P_2=1: 3\)
Question 34. A particle of mass M is moving in a horizontal circle of radius R with uniform speed v. When it moves from one point to a diametrically opposite point, it:
- kinetic energy change by Mv2/4
- momentum does not change
- momentum change by 2 Mv
- kinetic energy changes by mv²
Answer: 3. Momentum change by 2 Mv
∴ On the diametrically opposite points, the velocities have the same magnitude but opposite directions. Therefore change in momentum is Mv -(- Mv)= 2 Mv
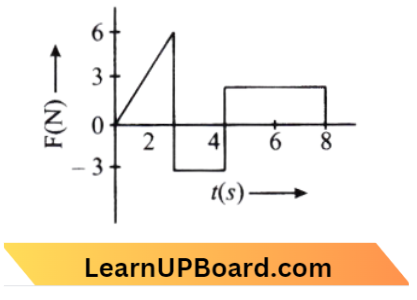
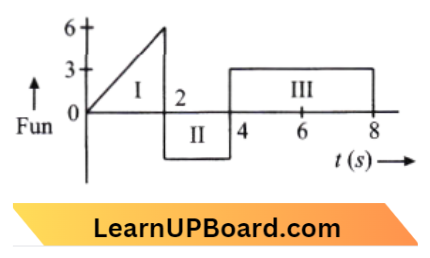
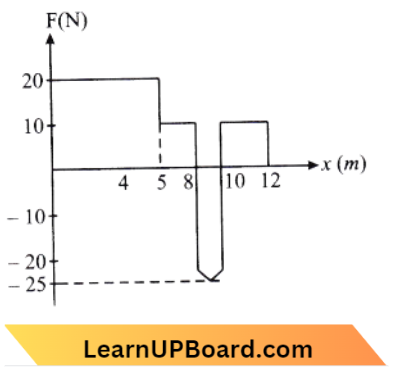
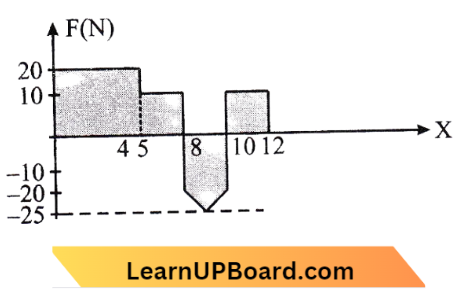
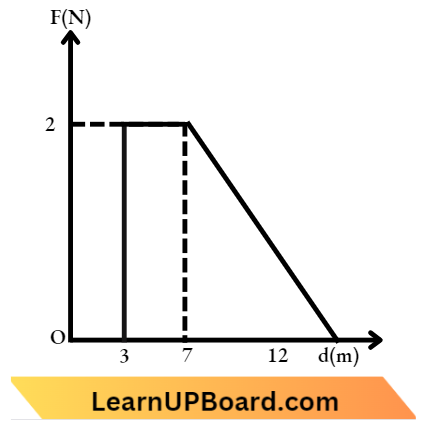
Question 35. Force F on a particle moving in a straight line varies with distance as shown in the figure. The work done on the particle during its displacement of 12 m is:
- 21 J
- 26 J
- 13 J
- 18 J
Answer: 3. 13 J
From Question,Work done = Area under (F – x) graph
=\(2 \times(7-3)+\frac{1}{2} \times 2 \times(12-7)\)
=\(8+\frac{1}{2} \times 10\)
=\(8+5=13 \mathrm{~J}\)
Question 36. A body of mass 3 kg is under a constant force which causes a displacement s in meters in it, given by the 1, relation s = \(\frac{1}{3} t^2\), where t is in seconds. Work done by the force in 2 seconds is:
- \(\frac{19}{5} \mathrm{~J}\)
- \(\frac{5}{19} \mathrm{~J}\)
- \(\frac{3}{8} \mathrm{~J}\)
- \(\frac{8}{3} \mathrm{~J}\)
Answer: 4. \(\frac{8}{3} \mathrm{~J}\)
It is given that:\(\mathrm{s}=\frac{t^2}{3}\)
Differentiating w.r.t. t, we have,
U=\(\frac{d s}{d t}=\frac{2 t}{3}\)
Again differentiating w.r.t. t, we have,
a=\(\frac{d^2 s}{d t^2}=\frac{2}{3}\)
Now, \(\mathrm{W}=\int \mathrm{F} d s =\int \mathrm{mads}\)
=\(\int_0^2 m \times \frac{2}{3} \times \frac{2 t}{3} d t\)
=\(\frac{4}{9} m \int^2 t d t\)
W =\(\frac{4}{9} m \times\left[\frac{t^2}{2}\right]_0^2\)
=\(\frac{4}{9} \times 3 \times 2=\frac{8}{3} \mathrm{~J}\)
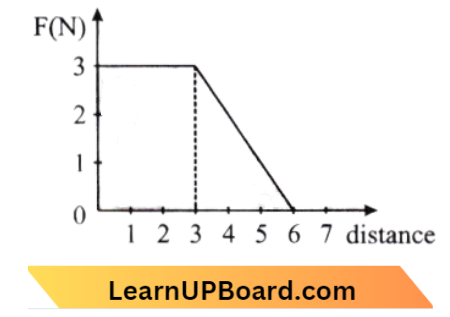
Question 37. A force F acting on an object varies with distance x as shown here. The force is in N and x in m. The work done by the force in moving the object x = 0 to x = 6m is:
- 18.0 J
- 13.5 J
- 9.0 J
- 4.5 J
Answer: 2. 13.5 J
Work done = Area under f – x curve.
= area of trapezium = \(\frac{1}{2} \times(6+3) \times 3=\frac{27}{2}=13.5 \mathrm{~J}\)
Question 38. A force acts on a 3.0 g particle in such a way that the position of the particle as a function of time is given by, x = 3t – 4t²- + t³, where x is in meter and nd t in second. The work done during the first 4s is:
- 570 mJ
- 450 mJ
- 490 mJ
- 528 mJ
Answer: 4. 528 mJ
Given,\( x=3 t-4 t^2+t^3\)
So, velocity v =\(\frac{d x}{d t}=3-8 t+3 t^2\)
⇒ \(\text { At } t=0 \mathrm{~s}\),
⇒ \(v_1 =3-0+0=3 \mathrm{~m} / \mathrm{s}\)
At \(t =4 \mathrm{~s}\),
⇒ \(v_2 =3-8 \times 4+3 \times 4^2\)
=\(3-32+48=19 \mathrm{~m} / \mathrm{s}\)
Now, from t=0 to t=4s
work done = gain in kinetic energy
=\(\frac{1}{2} m v_2^2-\frac{1}{2} m v_1^2\)
=\(\frac{1}{2} m\left(v_2^2-v_1^2\right)\)
=\(\frac{1}{2} \times 3 \times 10^{-3}\left[(19)^2-(3)^2\right]\)
⇒ [Using, \(a^2-b^2=(a+b)(a-b) ]\)
=\(1.5 \times 10^{-3} \times[(19+3)(19-3)]\)
=\(1.5 \times 10^{-3} \times 22 \times 16\)
=\(528 \times 10^{-3} \mathrm{~J}=528 \mathrm{~mJ}\)
Question 39. A position-dependent force F = (7 – 2x + 3x²) N, acts on a small body of mass 2 kg and displaces it from x = 0 to x = 5 m. Work done in joule is:
- 35
- 70
- 135
- 270
Answer: 3. 135
Work done by a variable force F in displacement from x = x¹ to x = x² = x is given by
⇒ \(\mathrm{W} =\int_{x_1}^{x_2} F(d x)\)
⇒ \(x_1 =0, x_2=5 \)
F =\(\left(7-2 x+3 x^2\right) \mathrm{N}\)
W =\(\int_0^5\left(7-2 x+3 x^2\right) d x\)
=\(\left[7 x-x^2+x^3\right]_0^5\)
=\(\left[7 \times 5-(5)^2+(5)^3\right]\)
=\([35-25+125]=135 \mathrm{~J}\)
Question 40. A body of mass m taken from the earth’s surface to the height equal to twice the radius (R) of the earth. The change in potential energy of the body will be:
- 2mgR
- mgR
- 3 mgR
- \(\frac{1}{3}\)mgR
Answer: 2. Mgr
According to the question, Change in potential energy
⇒ \(\Delta \mathrm{P} . \mathrm{E} =-\frac{G M m}{R+2 R}-\left(-\frac{G M m}{R}\right)\)
= \(-\frac{G M m}{3 R}-\frac{G M m}{R}=\frac{2 G M m}{3 R}\)
⇒ \(\Delta \mathrm{P} . \mathrm{E} =\frac{2}{3} m g R\)
Where, g =\(\frac{G M}{R^2}\)
Question 41. The potential energy of a particle in a force field is U =\(\mathrm{U}=\frac{A}{r^2}-\frac{B}{r}\) where A and B are positive constants and r is the distance of the particle form the center of the field. For stable equilibrium, the distance of the particle is:
- \(\frac{B}{2 A}\)
- \(\frac{2 A}{B}\)
- \(\frac{A}{B}\)
- \(\frac{B}{A}\)
Answer: 2. \(\frac{2 A}{B}\)
Here,\(\mathrm{U} =\frac{A}{r^2}-\frac{B}{r}\)
⇒ \(\frac{d U}{d r}\) =0
⇒ \(-\frac{2 A}{r^3}+\frac{B}{r^2}\) =0
or \(\frac{2 A}{r^3} =\frac{B}{r^2}\)
or r =\(\frac{2 A}{B}\)
Question 42. The potential energy of a system increases if work is done:
- by the system against a conservative force
- for the system against a conservative force
- upon the system by a conservative force
- against the system by a conservative force
Answer: 1. By the system against is a conservative force
The potential energy of a system increases. If work is done by the system against a conservative force.
⇒ \(\mathrm{W}_{\text {int }} =-\Delta \mathrm{U}\)
=\(-\left(\mathrm{U}_{\mathrm{f}}-\mathrm{U}_{\mathrm{i}}\right)\)
Question 43. The potential energy of a system increases if work is done:
- upon the system by nonconservative force
- by the system against a conservative force
- by the system against a nonconservative force
- upon the system by a conservative force.
Answer: 2. by the system against a conservative force
The work done by the system against a conservative force. Because we know that, \(-\Delta \mathrm{U}=\mathrm{W}_{\text {conservative force }}\)
Question 44. The potential energy between two atoms, in a molecule, is given by U (x) = \(\frac{a}{x^{12}}-\frac{b}{x^6}\)where a and b are positive and x is the distance between the atoms. The atom is in stable equilibrium, when:
- x=\(\left(\frac{2 a}{b}\right)^{1 / 6}\)
- \(x=\left(\frac{11 a}{5 b}\right)^{1 / 6}\)
- x=0
- x=\(\left(\frac{a}{2 b}\right)^{1 / 6}\)
Answer: 1. x=\(\left(\frac{2 a}{b}\right)^{1 / 6}\)
U(x)=\(\frac{a}{x^{12}}-\frac{b}{x^6}\)
or \(\frac{12 a}{x^{13}}-\frac{-6 b}{x^7}\)=0
or \( x^6=\frac{2 a}{b}\)
Therefore x=\(\left(\frac{2 a}{b}\right)^{1 / 6}\)
Question 45. Two similar springs P and Q have spring constant Kp and Kq, such that Kp > Kq. They are stretched, first by the same amount (case 1), then by the same force (case 2). The work done by the springs WP and WQ are related, in case and case (2), respectively:
- WP = WQ; WP > WQ
- WP = WQ; WP = WQ
- WP > WQ; WQ > WP
- WP < WQ; WQ < WP
Answer: 3. WP > WQ; WQ > WP
In case (1) elongation (x) is the same for both springs. So work done by springs P and Q is respectively.
⇒ \(W_P=\frac{1}{2} \mathrm{~K}_{\mathrm{P}} x^2 \text { and } W_Q=\frac{1}{2} \mathrm{~K}_{\mathrm{Q}} x^2\)
⇒ \(K_P>K_Q\)
⇒ \(W_P>W_Q\)
In case (2) force of elongation (F) is the same and so elongation is given by \(x_{\mathrm{P}}=\frac{F}{K_P} \text { and } x_{\mathrm{Q}}=\frac{F}{K_Q}[latex]\)
⇒ \(W_P=\frac{1}{2} k_{\mathrm{P}} x_P^2=\frac{1}{2} \frac{F^2}{k_P}\)
⇒ \(\mathrm{~W}_{\mathrm{Q}}=\frac{1}{2} k_{\mathrm{Q}} x_g^2=\frac{1}{2} \frac{\mathrm{F}^2}{k_g}\)
∴ \(W_P<W_Q\)
Question 46. A block of mass M is attached to the lower end of a vertical spring. The spring is hung from a ceiling and has force constant k. The mass is released from rest with the spring initially unstretched. The maximum extension produced in the length of the spring will be:
- \(\frac{2 M g}{k}\)
- \(\frac{4 M g}{k}\)
- \(\frac{M g}{2 k}\)
- \(\frac{M g}{k}\)
Answer: 1. \(\frac{2 M g}{k}\)
When the mass attached to a spring fixed at the other end is allowed to fall suddenly, it extends the spring by x. Potential energy lost by the mass is gained by the spring. \(m g x =\frac{1}{2} k x^2\)
x =\(-\frac{2 m g}{k}\)
Question 47. A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring so that the spring is compressed by a distance d. The net work done in the process is:
- \(m g(h+d)-\frac{1}{2} k d^2\)
- \(m g(h-d)-\frac{1}{2} k d^2\)
- \(m g(h-d)+\frac{1}{2} k d^2\)
- \(m g(h+d)+\frac{1}{2} k d^2\)
Answer: 1. \(m g(h+d)-\frac{1}{2} k d^2\)
Net work done = work done by gravitational force + work done by spring force \(m g(h+d)-\frac{1}{2} k d^2\)
Question 48. The potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:
- U/4
- 4 U
- W
- 16 U
Answer: 4. 16 U
Potential energy of a spring=\(\frac{1}{2} \times \text { force constant } \times(\text { extension })^2\)
Potential energy\(\propto(\text { extension })^2\)
Hence, \(\frac{U_1}{v_2}=\left(\frac{x_1}{x_2}\right)^2\)
⇒\(\frac{v_1}{v_2}=\left(\frac{2}{5}\right)^2\)
⇒ \(\frac{U_1}{U_2}=\frac{1}{16}\)
∴ \(U_2=16 U_1=16 v\)
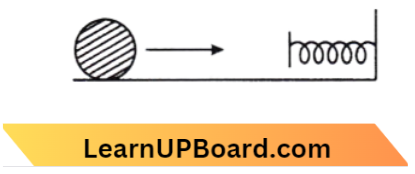
Question 49. A mass of 0.5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be:
- 0.15 m
- 0.12 m
- 1.5m
- 0.5m
Answer: 1. 0.15 m
According To Question , \(\frac{1}{2} m v^2 =\frac{1}{2} k x^2\)
x =\(v \sqrt{\frac{m}{k}}=1.5 \sqrt{\frac{0.5}{50}}\)
=\(0.15 \mathrm{~m}\)
Question 50. Two springs of spring constant k1 and k2 are joined in series. The effective spring constant of the combination is given by:
- \(\sqrt{k_1 k_2}\)
- \(\frac{\left(k_1+k_2\right)}{2}\)
- \(k_1+k_2\)
- \(\frac{k_1 k_2}{k_1+k_2}\)
Answer: 4. \(\frac{k_1 k_2}{k_1+k_2}\)
When the spring joined in series the total extension of spring is y=y1+y2
=\(\frac{-F}{k_1}-\frac{F}{k_2}\)
y =\(-\mathrm{F}\left[\frac{1}{k_1}+\frac{1}{k_2}\right]\)
∴ Spring Constant k =\(\frac{k_1 k_2}{k_1+k_2}\)
Question 51. A mass of 0.5 kg moving with a speed of 1.5 m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant k = 50 N/m. The maximum compression of the spring would be:
- 0.15 m
- 0.12 m
- 1.5 m
- 0.5 m
- Answer: 1. 0.15 m
The kinetic energy of Mass is converted into energy required to compress a spring which is given by
⇒ \(\frac{1}{2} m v^2 =\frac{1}{2} k x^2\)
x =\(v \sqrt{\frac{m}{k}}=1.5 \sqrt{\frac{0.5}{50}}\)
=0.15
Question 52. When a long spring is stretched by 2 cm, its potential energy is U. If the spring is stretched by 10 cm, the potential energy stored in it will be:
- \(\frac{U}{5}\)
- 5U
- 10U
- 25U
Answer: 4. 25U
U=\(\frac{1}{2}\)
⇒ \(K(2)^2\)
⇒ \(U^{\prime}=\frac{1}{2} K(10)^2\)
From above equations (1) and (2) \(U^{\prime}=25 \mathrm{U}\)
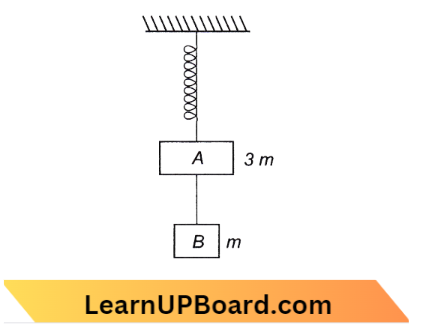
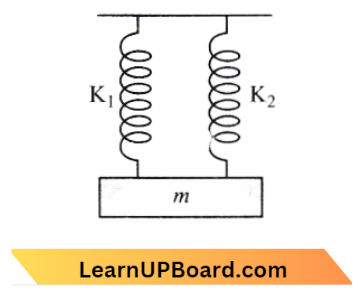
Question 53. A mass is suspended separately by two different springs in successive order, and then the period is T1 and T2, respectively. If it is connected by both springs as shown in the figure, then the period T0, so the correct equation is:
- \(T_0^2=T_1^2+T_2^2\)
- \(T_0^{-2}=T_1^{-2}+T_2^{-2}\)
- \(T_0^{-1}=\mathrm{T}_1^{-1}+\mathrm{T}_2^{-1}\)
- \(T_0=T_1+T_2\)
Answer: 2. \(T_0^{-2}=T_1^{-2}+T_2^{-2}\)
Time period of spring,T=\(2 \pi \sqrt{\frac{m}{\mathrm{~K}}}\)
K=\(4 \pi^2 \frac{m}{T^2}\)
⇒ \(K \propto \frac{1}{T^2}\)
For a parallel combination of spring \(K =K_1+K_2\)
⇒ \(\frac{1}{T_0^2} =\frac{1}{T_1^2}+\frac{1}{T_2^2}\)
∴ \(T_0^{-2} =T_1^{-2}+T_2^{-2}\)
Question 54. Two springs A and B having spring constant KA and KB (KA = 2 KB) are stretched by applying a force of equal magnitude. If energy stored in spring A is EA then energy stored in B will be:
- 2 EA
- EA/4
- EA/2
- 4 EA
Answer: 1. 2 EA
⇒ \(\frac{1}{2} K x^2 =\frac{1}{2} \frac{F^2}{K}\)
⇒ \(\frac{K_A}{K_B}\) =2
∴ \(\frac{E_A}{E_B} =\frac{1}{2} \text { or } \mathrm{E}_{\mathrm{B}}=2 \mathrm{E}_{\mathrm{A}}\)
Question 55. The energy that will be ideally radiated by a 100 kW transmitter in 1 hour is:
- 36 x 104 J
- 36 x 105 J
- 1 x 105 J
- 36 x 107 J
Answer: 4. 36 x 107 J
Given, P= 100 kW
Time, t= 1 hour
E = Pxt= 100x 1 = 100 kWh
E = 100 x 3.6 x 106 J = 36 x 107J ( v1 kWh = 3.6 x 106J)
Question 56. Light with an average flux of 20 W/cm² falls on a non-reflecting surface at normal incidence having a surface area of 20 cm². The energy received on the surface during 1 min is:
- 12 x 10³ J
- 24 x 10³ J
- 48 x 10³ J
- 10 x 10³ J
Answer: 2. 24 x 10³ J
From the question, average flux = 20 W/cm², surface area 20 cm²
Time = 1 min = 60 s For non-reflecting surface
Energy received = average flux x surface area x time
= 20 x 20 x 60
= 24 x 103 J.
Question 57. The energy required to break one bond in DNA is 10-20 J. This value (in eV) is nearly:
- 0.6
- 0.062
- 0.006
- 6
Answer: 2. 0.062
The energy in electron volts is given as lev = 1.602 x 10-19 J
The energy required to break the DNA bond is 10-20J. So, the energy in terms of eV will be:
⇒ \(10^{-20} \mathrm{~J} =\frac{1}{1.602 \times 10^{-19}} \times 10^{-20} \mathrm{eV}\)
∴ \(\mathrm{E}_{e v} =0.062 \mathrm{eV}\)
Question 58. A particle of mass m is driven by a machine that delivers a constant power of k watts. If the particle starts from rest, the force on the particle at time t is:
- \(\sqrt{\frac{m k}{2}} t^{-1 / 2}\)
- \(\sqrt{m k} t^{-1 / 2}\)
- \(\sqrt{2 m k} t^{-1 / 2}\)
- \(\frac{1}{2} \sqrt{m k} t^{-1 / 2}\)
Answer: 1. \(\sqrt{\frac{m k}{2}} t^{-1 / 2}\)
According to the question. The machine delivers constant power
F. v = Constant
⇒ \(\frac{d v}{d t} \cdot v=\mathrm{K}\)
⇒ \(\int v d v=\frac{k}{m} \int d t\)
⇒ \(\frac{v^2}{2}=\frac{k}{m} t \Rightarrow v=\sqrt{\frac{2 k t}{m}}\)
force on the particle is F=\(m \frac{d v}{d t}=m \frac{d}{d t}\left(\sqrt{\frac{2 k t}{m}}\right)\)
=\(\sqrt{2 k m} \cdot\left(\frac{1}{2} t^{-1 / 2}\right)=\sqrt{\frac{m k}{2}} \cdot t^{-1 / 2}\)
Question 59. 300 J of work is done in sliding a 2 kg block up an inclined plane of height 10 m. Taking, g = 10 m/s², work done against friction is:
- 1000 J
- 200 J
- 100J
- Zero
Answer: 3. 100J
Potential energy, P.E. = 2 x 10 x 10 = 200 J
and workdone w = 300 J.
Work done against friction = 300-200= 100 J.
Question 60. An electric lift with a maximum load of 2000 kg (lift + passengers) is moving up with a constant speed of 1.5 ms-1. The minimum power delivered by the motor to the lift in watts is (g = 10 ms-2):
- 20000
- 34500
- 23500
- 23000
Answer: 2. 34500
Given: v = 1.5 m/s
m = 2000 kg F = 3000 N
Here we are given that the velocity is constant, and acceleration is defined as the rate of change of velocity concerning time, therefore for the constant velocity the acceleration (a) is zero, a = 0
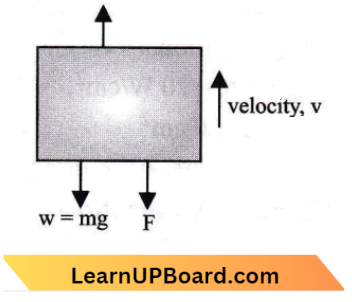
The figure of an electric lift is shown below:
Therefore, The tension T = W + F ⇒ T = 2000 x 10 + 3000
T = 20000 + 3000
T = 23000 N
Now, using equation (1) we have; P = Tv
P = 23000 x 1.5
P = 34500 watts.
Question 61. Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of the input energy. How much power is generated by the turbine? (g = 10 m/s²)
- 10.2 kW
- 8.1 kW
- 12.3 kW
- 7.0 kW
Answer: 2. 8.1 kW
Given, Height (h) = 60 m
Mase/time = 15 kg/s
Loss = 10% ri = 90%
P = ? if g = 10 ms²
⇒ \(\text { Power }=\frac{\text { work }}{\text { time }}\)
=\(\frac{m g h}{t} \eta\)
⇒ \(\mathrm{P}=15 \times 16 \times 60 \times \frac{9}{16}\)
= 900 x 9 = 8100 J/S P = 8.1 kW
Question 62. A particle of mass M starting from rest undergoes uniform acceleration. If the speed acquired in time T is V, the power delivered to the particle is:
- \(\frac{M v^2}{T}\)
- \(\frac{1}{2} \frac{M v^2}{T^2}\)
- \(\frac{M v^2}{T^2}\)
- \(\frac{1}{2} \frac{M v^2}{T}\)
Answer: 4. \(\frac{1}{2} \frac{M v^2}{T}\)
K.E. of particle=\(\frac{1}{2} \mathrm{Mv}^2\)
⇒ \(\text { Power } =\frac{\text { Energy }}{\text { Time }}\)
∴ \(\mathrm{P} =\frac{1}{2} \frac{M v^2}{t}\)
Question 63. A body of mass 1 kg begins to move under the action of a time-dependent force F =\(\left(2 t \hat{i} \times 3 t^2 \hat{j}\right)\) N, where \(\hat{i}\) and \(\hat{j}\) are unit vectors along X and Y-axis. What power will be developed by the force at the time (t)?
- (2t² + 4t4) W
- (2t3 + 3t4) W
- (2t3 + 3t4) W
- (2t + 3t3) W
Answer: 3. (2t3 + 3t4) W
From the question, A body of mass 1 kg begins to move under the action of a time-dependent force isF=\(\left(2 t \hat{i}+3 t^2 \hat{j}\right) \mathrm{N}\)
F=ma
a=\(\frac{F}{m} \text { and } \mathrm{m}=1 \mathrm{~kg}\)
a=\(\left(2 \hat{i}+3 t^2 \hat{j}\right) \mathrm{m} / \mathrm{s}^2\)
a=\(\frac{d v}{d t}\)
DV = adt
⇒ \(\int d v=\int a d t\)
v=\(\int\left(2 t \hat{i}+3 t^2 \hat{j}\right) d t=t^2 \hat{i}+t^3 \hat{j}\)
⇒ \(\text { Power, } P=F \cdot v\)
= \(\left(2 \hat{t} \hat{i}+3 t^2 \hat{j}\right) \cdot\left(t^2 \hat{t}+t_3 \hat{j}\right)\)
P=\(\left(2 t^3+3 t^5\right) \mathrm{W}\)
Question 64. One coolie takes 1 minute to raise a suitcase through a height of 2m but the second coolie takes 30 s to raise the same suitcase to the same height. The power two coolies are in the ratio of
- 1 : 3
- 2: 1
- 3 :1
- 1: 2
Answer: 4. 1: 2
We know that,\(\text { Power }=\frac{\text { Work done }}{\text { Time }}\)
Work done = mgh,
In same in both the case \(\frac{\mathrm{P}_1}{\mathrm{P}_2}=\frac{f_2}{f_1}\)
=\(\frac{30 \mathrm{sec}}{1 \mathrm{~min}}=\frac{1}{2}\)
Question 65. An engine pumps water through a hose pipe. Water passes through the pipe and leaves it with a velocity of 2 ms-1. The mass per unit length of water in the pipe is 100 km-1. What is the power of the engine?
- 400 W
- 200 W
- 100 W
- 800 W
Answer: 4. 800 W
We know that P=FV=maV
= \(m \times \frac{v}{t} \times v=\left(\frac{m}{l}\right)_t^l . v . v\)
⇒ \(\frac{m}{l}= \text { mass per unit }\)
= \(100 \text { (given) }\)
= \((100)\left(2^3\right)=800 \mathrm{w}\)
Question 66. Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional forces are 10% of energy. How much power is generated by the turbine? (g= 10 m/s²)
- 8.1 kW
- 10.2 kW
- 12.3 kW
- 7.0 kW
Answer: 1. 8.1 kW
Given
Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional forces are 10% of energy.
Power generated by the turbine is, \(P_{\text {generated }}=P_{\text {input }} \times \frac{90}{100}=\frac{M g h}{t} \times \frac{90}{100}\)
Putting the given value, \(\frac{M}{t}=15 \mathrm{~kg} / \mathrm{s}, \mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\)
and h=60
P=\((15 \times 10 \times 60) \times \frac{90}{100}=8.1 \mathrm{kw}\)
Question 67. A shell of mass m is at rest initially. It explodes into three fragments having mass in the ratio 2: 2: 1. If the fragments having equal mass fly off in mutually perpendicular directions with speed v, the speed of the third (lighter) fragment is:
- \(\sqrt{2} v\)
- \(2 \sqrt{2} v\)
- \(3 \sqrt{2} v\)
- v
Answer: 2. \(2 \sqrt{2} v\)
Given
A shell of mass m is at rest initially. It explodes into three fragments having mass in the ratio 2: 2: 1. If the fragments having equal mass fly off in mutually perpendicular directions with speed v
The total mass of the shell is m.
The ratio of the masses of the fragments is 2 : 2: 1
2x + 2x + x = m
x = 0.2m
Let the velocity of the lighter fragment be v ‘
⇒ \(\mathrm{P}^{\prime} =\sqrt{P_1^2+P_2^2}\)
⇒ \(0.2 m v^{\prime} =\sqrt{(0.4 m v)^2+(0.4 m v)^2}\)
⇒ \(0.2 m v^{\prime} =\sqrt{2} \times 0.4 m v\)
∴ \(v^{\prime} =2 \sqrt{2} v\)
Question 68. A mass of m moving horizontally (along the x-axis) with velocity v collides and strikes to mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is:
- \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)
- \(\frac{1}{3} v \hat{i}+\frac{2}{3} v \hat{j}\)
- \(\frac{2}{3} v \hat{i}+\frac{1}{3} v \hat{j}\)
- \(\frac{3}{2} v \hat{i}+\frac{1}{4} v \hat{j}\)
Answer: 1. \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)
⇒ \(m v+(3 m)(2 v) =(4 m) v^{\prime}\)
⇒ \(m v \hat{i}+6 m v \hat{j} =4 m v^{\prime}\)
⇒ \(v^{\prime} =\frac{1}{4} v \hat{i}+\frac{6}{4} v \hat{j}\)
=\(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)
Question 69. Body A of mass 4 m moving with speed u collides with another body B of mass 2 m, at rest. The collision is head-on-end elastic. After the collision, the fraction of energy lost by the colliding body A is:
- \(\frac{8}{9}\)
- \(\frac{4}{9}\)
- \(\frac{5}{9}\)
- \(\frac{1}{9}\)
Answer: 1. \(\frac{8}{9}\)
Given
Body A of mass 4 m moving with speed u collides with another body B of mass 2 m, at rest. The collision is head-on-end elastic.
Fractional loss of KE. of the colliding body is \(\frac{4 \mathrm{KE}}{\mathrm{KE}}=\frac{4\left(m_1 m_2\right)}{\left(m_1+m_2\right)^2} =\frac{4(m)(2 m)}{(4 m+2 m)^2}\)
=\(\frac{32 m^2}{36 m^2}=\frac{8}{9} .\)
Question 70. Body A of mass 4 m moving with speed u collides with another body B of mass 2 m, at rest. The collision is head-on-end elastic. After the collision, the fraction of energy lost by the colliding body A is:
- \(\frac{5}{9}\)
- \(\frac{1}{9}\)
- \(\frac{8}{9}\)
- \(\frac{4}{9}\)
Answer: 3. \(\frac{8}{9}\)
According to the conservation of momentum, \(4 m u_1=4 m v_1+2 m v_2\)
⇒ \(2\left(u_1-v_1\right)=v_2\) → Equation – 1
From conservation of energy, \(\frac{1}{2}(4 m) u_1^2=\frac{1}{2}(4 m) v_1^2+\frac{1}{2}(2 \mathrm{~m}) v_2^2\)
⇒ \(2\left(u_1^2-v_1^2\right)=v_2^2\) → Equation – 2
From 1 and 2,
⇒ \(2\left(u_1^2-v_1^2\right)=4\left(u_1-v_1\right)^2\)
⇒ \(3 v_1=u_1\) Equation – 3
Now, a fraction of loss in kinetic energy for mass 4 m, \(\frac{\Delta k}{k_i}=\frac{k_i-k_f}{k_i}\)
=\(\frac{\frac{1}{2}(4 m) u_1^2-\frac{1}{2}(4 m) v_1^2}{\frac{1}{2}(4 m) u_1^2}\) Equation – 4
Substituting 3 in 4, we get \(\frac{\Delta K}{K_i}=\frac{8}{9}\)
Question 71. A moving block having a mass of m collides with another stationary block having a mass of 4 m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is v, then the value of the coefficient of restitution (e) will be:
- 0.8
- 0.25
- 0.5
- 0.4
Answer: 2. 0.25
According to the law of conservation of linear momentum, we have, m1U1+ m2u2 = m1V1 + m2v2. Equation -1
Where m1 and m2 are the masses of two bodies, their initial velocities are u1 and u2, and final velocities are v1 and v2 respectively in the equation m1 = m2 = 4m
u1 = V1 u2 = 0 and v1 = 0
In equation. 1,
mv + 4m x 0 = 0 + 4 mv2
⇒ \(\quad v_2=\frac{v}{4}\)
Now coefficient of restitution e,
e=\(\frac{\text { Relative velocity of separation }}{\text { Relative velocity of approach }}=\frac{\frac{v}{4}}{v}\)
e=\(\frac{1}{4}=0.25\)
Question 72. Two identical balls A and B having velocities of 0.5 m/s and – 0.3 m/s respectively, collide elastically in one dimension. The velocities of B and A after the collision respectively will be:
- – 0.5 m/s and 0.3 m/s
- 0.5 m/s and 0.3 m/s
- – 0.3 m/s and 0.5 m/s
- 0.3 m/s and 0.5 m/s
Answer: 3. – 0.3 m/s and 0.5 m/s
Since both bodies are identical and collision is elastic. Therefore velocities will be interchanged after collision.
vA = – 0.3 m/s and vB = 0.5 m/s
Question 73. A bullet of mass 10 g moving horizontally with a velocity of 400 m s-1 strikes a wooden block of mass 2 kg which is suspended by light in an extensible string of length 5 m. As a result, the center of gravity of the block is found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges horizontally from the block will be:
- 100 ms-1
- 80 ms-1
- 120 ms-1
- 160 ms-1
Answer: 3. 120 ms-1
Mass of bullet,m= 10 g=0.01 kg
The initial speed of a bullet, u=400 ms-1
Mass of block, M=2 kg
Length of string, l= 5 m
Speed of the block after collision = v1
Speed of the bullet on emerging from block, v=?
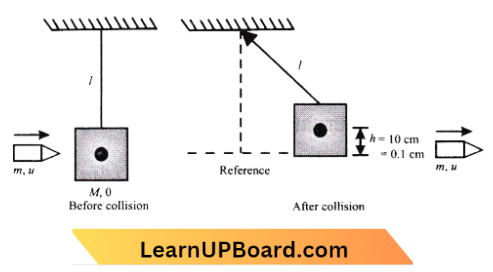
Using the energy conservation principle from the block,
⇒ \((\mathrm{KE}+\mathrm{PE})_{\text {Reference }}=(\mathrm{KE}+\mathrm{PE})_{\mathrm{h}}\)
⇒ \(\frac{1}{2} \mathrm{M} v_1^2=\mathrm{Mgh}\) or
⇒ \(v_1=\sqrt{2 g h}\)
⇒ \(v_1=\sqrt{2 \times 10 \times 0.1}=\sqrt{2} \mathrm{~m} \mathrm{~s}^{-1}\)
Using the momentum conservation principle for block and bullet systems,
⇒ \((M \times 0+m u)_{\text {Before collision }} =\left(M \times v_1+m v\right)_{\text {after collision }}\)
⇒ \(0.01 \times 400 =2 \frac{1}{2}+0.01 \times v\)
v =\(\frac{4-2 \sqrt{2}}{0.01}\)
=\(117.15 \mathrm{~m} \mathrm{~s}^{-1} \approx 120 \mathrm{~m} \mathrm{~s}^{-1}\)
Question 74. Two particles of masses m1, and m2 move with initial velocities u1 and u2. On collision, one of the particles gets excited to a higher level, after absorbing energy If the final velocities of particles are v1 and v2 then we must have:
- \(m_1^2 u_1+m_2^2 u_2-\mathrm{E}=m_1^2 v_1+m_2^2 v_2\)
- \(\frac{1}{2} m_1^2 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m^2 v_2^2-\mathrm{E}\)
- \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\mathrm{E}=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)
- \(\frac{1}{2} m_1^2 u_1^2+\frac{1}{2} m_2^2 u_2^2+\mathrm{E}=\frac{1}{2} m_1^2 v_1^2+\frac{1}{2} m_2^2 v_2^2\)
Answer: 3. \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\mathrm{E}=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)
Let, m1, m2 be the masses of particles u1, u2 be the initial velocities of particles and v1, V2 be the final velocities of particles
from the law of conservation of energy
Initial total energy = final total energy
∴ \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2+\mathrm{E}\)
Question 75. A ball is thrown vertically downwards from a height of 20 m with an initial velocity of VQ. It collides with the ground, loses 50% of its energy in a collision, and rebounds to the same height. The initial velocity v0 is: (Take, g = 10 ms-2)
- 14 ms-1
- 20 ms-1
- 28 ms-1
- 10 ms-1
Answer: 2. 20 ms-1
Let v be the speed of the ball then \(v=\sqrt{2 g h}=\sqrt{2 \times 10 \times 20}=20 \mathrm{~m} / \mathrm{s}\)
Now the energy of a ball just after rebound \(E=\frac{1}{2} m v^2=200 \mathrm{~m}\)
According to the question, 50% of energy cases in a collision means just before collision energy is 400 m.
Using law of conservation of energy,\(\frac{1}{2} m v_0^2+m g h=400\)
⇒ \(\frac{1}{2} m v_0^2+m \times 10 \times 20\)=400
∴ \(v_0 =20 \mathrm{~m} / \mathrm{s}\)
Question 76. On a frictionless surface, a block of mass M moving at speed v collides elastically with another block of the same mass M which is initially at rest. After the collision, the first block moves at an angle θ to its initial direction and has a speed \(\frac{v}{3}\). The second block’s speed after the collision is:
- \(\frac{2 \sqrt{2}}{3} v\)
- \(\frac{3}{4} v\)
- \(\frac{3}{\sqrt{2}} v\)
- \(\frac{\sqrt{3}}{2} v\)
Answer: 1. \(\frac{2 \sqrt{2}}{3} v\)
According to the question, Using Law Of Conservation of Kinetic Energy
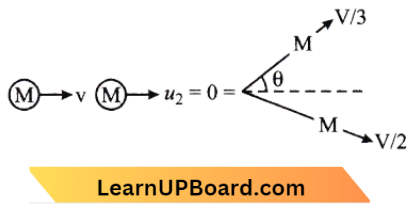
⇒ \(\frac{1}{2} M v^2+0=\frac{1}{2} M\left(\frac{v}{3}\right)^2+\frac{1}{2} M v_2^2\)
⇒ \(v^2=\frac{v^2}{9}+v_2^2\)
⇒ \(v_2^2=\frac{8 v^2}{9}\)
∴ \(v_2=\frac{2 \sqrt{2}}{3} v\)
Question 77. Two particles A and B, move with constant velocities \(\vec{r}_1 \text { and } \overrightarrow{r_2}\). At the initial moment their position vectors are \(\vec{r}_1 \text { and } \overrightarrow{r_2}\) respectively. The condition for particles A and B for their collision is:
- \(\overrightarrow{r_1} \times \overrightarrow{v_1}=\overrightarrow{r_2} \times \overrightarrow{v_2}\)
- \(\overrightarrow{r_1}-\overrightarrow{r_2}=\overrightarrow{v_1}-\overrightarrow{v_2}\)
- \(\frac{\overrightarrow{r_1}-\overrightarrow{r_2}}{\left|\overrightarrow{r_1}-\overrightarrow{r_2}\right|}=\frac{\overrightarrow{v_2}-\overrightarrow{v_1}}{\left|\overrightarrow{v_2}-\overrightarrow{v_1}\right|}\)
- \(\overrightarrow{r_1}, \overrightarrow{v_1}=\overrightarrow{r_2}, \overrightarrow{v_1}\)
Answer: 3. \(\frac{\overrightarrow{r_1}-\overrightarrow{r_2}}{\left|\overrightarrow{r_1}-\overrightarrow{r_2}\right|}=\frac{\overrightarrow{v_2}-\overrightarrow{v_1}}{\left|\overrightarrow{v_2}-\overrightarrow{v_1}\right|}\)
Let the particles A and B collide at time t. For their collision, the position vectors of both particles should be the same at time t,\(\vec{r}_1+\vec{v}_1 t=\vec{r}_2+\vec{v}_2 t\)
⇒ \(\vec{r}_1-\vec{r}_2 \approx \vec{v}_2 t-\vec{v}_1 t =\left(\vec{v}_2-\vec{v}_1\right) t\) Equation – 1
⇒ \(\left|\vec{r}_1-\vec{r}_2\right| =\left|\vec{v}_2-\vec{v}_1\right| t\)
or t =\(\frac{\left|\vec{r}_1-\vec{r}_2\right|}{\left|\vec{v}_2-\vec{v}_1\right|}\)
Substituting this value of t in eqn. 1, we get,
∴ \(\vec{r}_1-\vec{r}_2=\left(\vec{v}_2-\vec{v}_1\right) \frac{\left|\vec{r}_1-\vec{r}_2\right|}{\left|\vec{v}_2-\vec{v}_1\right|}\)
Question 78. A ball is thrown vertically downwards from a height of 20 m with an initial velocity of v0. It collides with the ground, loses 50 percent of its energy in a collision, and rebounds to the same height. The initial velocity v0 is (Take g = 10 m s²):
- 28 m s-2
- 10 m s-2
- 14 ms-2
- 20 m s-2
Answer: 4. 20 m s-2
The situation is shown in the figure.
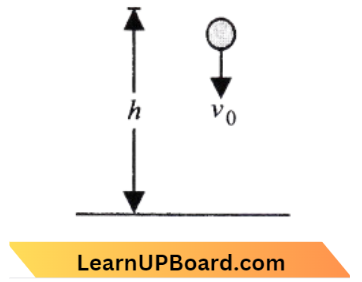
Let v be the velocity of the ball with which it collides with the ground. Then according to the law of conservation of energy,
The gain in kinetic energy = loss in potential energy
⇒ \(\frac{1}{2} m v^2-m v_0^2=m g h\) (where m is the mass of the ball) → Equation 1
Now, when the ball collides with the ground, 50% of its energy is lost and it rebounds to the same height h
⇒ \(\frac{50}{100}\left(\frac{1}{2} m v^2\right) =m g h\)
⇒ \(\frac{1}{4} v^2 =g h\)
or \(v^2 =4 g h\)
Substituting this value of v² in eqn. (1), we get \(4 g h-v_0^2=2 g h\)
Here, \(\mathrm{g}=10 \mathrm{~ms}^{-1} and h=20 \mathrm{~m}\)
∴ \(v_0 =\sqrt{2\left(10 \mathrm{~ms}^{-1}\right)(20 m)} 20 \mathrm{~ms}^{-1} =20 \mathrm{~ms}^{-1}\)
Question 79. On a frictionless surface, a block of mass M moving at speed v collides elastically with another block of the same mass M which is initially at rest. After the collision, the first block moves at an angle θ to its initial direction and has a speed of v/3. The second block’s speed after the collision is:
- \(\frac{3}{\sqrt{2}} v\)
- \(\frac{\sqrt{3}}{2} v\)
- \(\frac{2 \sqrt{2}}{3} v\)
- \(\frac{3}{4} v\)
Answer: 3. \(\frac{2 \sqrt{2}}{3} v\)
The situation is shown in the figure.
Let v’ be the speed of the second block after the collision. As the collision is elastic, so kinetic energy is conserved. According to the conservation of kinetic energy,
⇒ \(\frac{1}{2} M v^2+0 =\frac{1}{2} M\left(\frac{v}{3}\right)^2+\frac{1}{2} M v^{\prime 2}\)
∴ \(v^2 =\frac{v^2}{9}+v^{\prime} 0^2\)
Question 80. Two spheres A and B of masses my and m2 respectively collide. A is at rest initially and after collision B has a velocity \(\frac{v}{2}\) in a direction perpendicular to the original direction. The mass A moves after collision in the direction:
- same as that of B
- opposite to that of B
- a = tan-1 \(\left(\frac{1}{2}\right)\) to the x-axis
- a = tan-1 \(\left(\frac{-1}{2}\right)\)to the x-axis
Answer: 1. same as that of B
There is no external force acting on the spheres. So linear momentum will be conserved.
Before the collision, In direction x, Linear momentum = m2v → Equation 1
In direction y, Linear momentum = 0
After the collision, the spheres move as shown in the figure, let the velocity of sphere A be v1
In direction x, Linear momentum = m1v1cos(θ) → Equation …(2)
In direction y, Linear momentum = \(\frac{m_2 v}{2} m_1 v_1 \sin (\theta)\) → Equation 3
Linear momentum will be conserved, From equations 1 and 2, m1v1cosθ=0
From the equation 2,\(\frac{m_2 v}{2} m_1 v_1 \sin (\theta)\)=0
⇒ \(=m_1 v_1 \sin (\theta)=\frac{m_2 v}{2}\) Equation 5
Dividing equation 5 by 4,
⇒ \(\tan (\theta) =\frac{1}{2}\)
∴ \(\theta =\tan ^{-1}\left(\frac{1}{2}\right)\) Equation 5
Question 81. A mass m moving horizontally (along the x-axis) with velocity v collides and sticks to a mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is:
- \(\frac{3}{4} v \hat{i}+\frac{1}{4} v \hat{j}\)
- \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)
- \(\frac{1}{3} v \hat{i}+\frac{2}{3} v \hat{j}\)
- \(\frac{2}{3} v \hat{i}+\frac{1}{3} v \hat{j}\)
Answer: 2. \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)
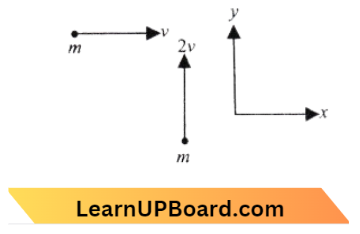
According to conservation of momentum, we get\(m v^{\frac{2 a}{b}}+(3 m) 2 v^{\left(\frac{2a}{b}\right)^{\prime 1/6}}=(m+3 m) \overrightarrow{v^{\prime}}\)
where v ‘ is the final velocity after collision\(\overrightarrow{v^{\prime}}=\frac{1}{4} v \hat{i}+\frac{6}{4} v \hat{j}=\frac{1}{4} v \hat{i}+\frac{3}{4} v \hat{j}\)
Question 82. A ball moving with velocity ms-1 collides head-on with another stationery ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in ms-1) after the collision will be:
- 0, 1
- 1, 1
- 1,0.5
- 0,2
Answer: 1. 0, 1
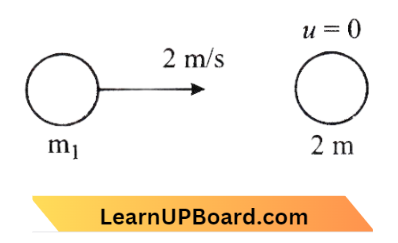
The situation is shown as :\(v_1=\frac{\left(m_1-e m_2\right)}{m_1+m_2} u_1+0 \times u_2\)
∴ \(v_1=\left[\frac{m-(0.5)(2 m)}{3 m}\right]\)=0
Question 83. Two equal masses m1 and m2 moving along the same straight line with velocities + 3 m/s and -5 m/s respectively collide elastically. Their velocities after the collision will be respectively:
- – 4 m/s and + 4 m/s
- + 4 m/s for both
- – 3 m/s and + 5 m/s
- – 5 m/s and + 3 m/s
Answer: 4. – 5 m/s and + 3 m/s
Equal masses after elastic collision interchanges their velocities. – 5 m/s and + 3 m/s.
Question 84. A rubber ball is dropped from a height of 5 m on a plane. On bouncing it rises to 1.8 m. The ball loses its velocity on bouncing by a factor of:
- \(\frac{3}{5}\)
- \(\frac{2}{5}\)
- \(\frac{16}{25}\)
- \(\frac{9}{25}\)
Answer: 1. \(\frac{3}{5}\)
Initial energy equation \(m g h=\frac{1}{2} m v^2 \text { i.e. } 10 \times 5=\frac{1}{2} v_1^2\)
V1=10
After one Bounce,\(10 \times 1.8=\frac{1}{2} v_2^2\)
v2=6
∴ Loss in velocity On bouncing \(\frac{6}{10}=\frac{3}{5}\)
Question 85. A metal ball of mass 2 kg moving at the speed of 36 km/h has a head-on collision with a stationary ball of mass 3 kg. If after collision, both the balls move as a single mass, then the loss in K.E. due to collision is:
- 100 J
- 140 J
- 40 J
- 60 J.
Answer: 4. 60 J
Mass of metal ball = 2 kg;
Speed of metal ball (v1) = 36 km/h = 10 m/s and
mass of stationary ball = 3 kg
Applying law of conservation of momentum, m1v1 + m2v2 = (m1 + m2)v
or \(\mathrm{v} =\frac{m_1 v_1+m_2 v_2}{m_1+m_2}\)
=\(\frac{(2 \times 10)+(3 \times 0)}{2+3}=\frac{20}{5}=4 \mathrm{~m} / \mathrm{s}\)
Question 86. A moving body of mass m and velocity 3 km/hour collides with a body at rest of mass 2m and sticks to it. Now the combined mass starts to move. What will be the combined velocity?
- 3 km/hour
- 4 km/hour
- 1 km/hour
- 2 km/hour
Answer: 3. 1 km/hour
Mass of body (m1) = m;
Velocity of first body (u1) = 3 km/hour;
Mass of second body at rest (m2) = 2m and velocity of second body (u2) = 0.
After combination, mass of the body M= m + 2m = 3m
From the law of conservation of momentum, we get Mv = m1U1 + m2u2
or 3mv = (m x3) + (2m x 0) = 3m
or v = 1 km/hour.
Question 87. The coefficient of restitution e for a perfectly elastic collision is:
- 1
- zero
- infinite
- -1
Answer: 1. 1
A quantity known as the coefficient of restitution or coefficient of resilience of the collision determines the degree of elasticity of the impact. It is defined as the ratio of relative separation velocity after a collision to relative approach velocity before a collision. It is denoted by the letter e. relative velocity of separation (after collision)
=\(\frac{\text { relative velocity of separation(after collision) }}{\text { relative velocity of approach (before collision) }}\)
⇒\(e=\frac{v_2-v_1}{u_1-u_2}\)
where, u1 and u2 are the velocities of two bodies before collision, and u1, and u2 are the velocities of the two bodies after the collision. The relative velocity of separation after a perfectly elastic collision is equal to the relative velocity of the approach before the collision.
∴ e = 1