Gravitation MCQs for NEET

Gravitation

Question 1. A mass falls from a height ‘h’ and its time of fall ‘t’ is recorded in terms of time T of a simple pendulum. On the surface of Earth, it is found that t = 2 T. The entire set-up is taken on the surface of another planet whose mass is half of Earth and whose radius the same. The same experiment is repeated and corresponding times as t’ and T’:

1. \(t^{\prime}=\sqrt{2} \mathrm{~T}^{\prime}\)
2. \(t^{\prime}>2 \mathrm{~T}^{\prime}\)
3. \(t^{\prime}<2 \mathrm{~T}^{\prime}\)
4. \(t^{\prime}=2 \mathrm{~T}\)

Answer: 1. \(t^{\prime}=\sqrt{2} \mathrm{~T}^{\prime}\)

Force surface of Earth time taken is falling h distance t=\(\sqrt{\frac{2 h}{g}} \text { and } T=2 \pi \sqrt{\frac{l}{g}}\)

Given, t=\(2 T\)

⇒ \(\frac{t}{T}\)=2

For surface of other planet, \(g^{\prime}=\frac{g}{2}\)

Time taken in falling h distance, \(t^{\prime}=\frac{2 h}{g}=\sqrt{2} t\)

and \(T=2 \pi \sqrt{\frac{1}{g^{\prime}}}=\sqrt{2} T\)

Here \(\frac{t^{\prime}}{T^{\prime}}=\frac{\sqrt{2} t}{\sqrt{12} T}\)=2

∴ \(t^{\prime}=2 T^{\prime}\)

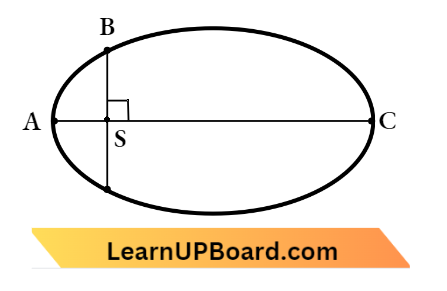
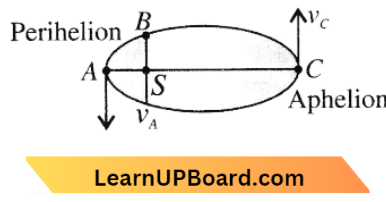
Question 2. The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are D_A, K_B and K_C respectively, AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then

1. \(t^{\prime}=\sqrt{2} \mathrm{~T}^{\prime}\)
2. \(t^{\prime}>2 \mathrm{~T}^{\prime}\)
3. \(t^{\prime}<2 \mathrm{~T}^{\prime}\)
4. \(t^{\prime}=2 \mathrm{~T}\)

Answer: 2. \(t^{\prime}>2 \mathrm{~T}^{\prime}\)

Point A is perihelion and C is aphelion.

So,\( V_A>V_B>V_C\)

As kinetic energy \(\mathrm{K}=(1 / 2) m v^2\) or \(K \propto v^2\)

So, \(K_A>K_B>K_C\)

Read and Learn More NEET Physics MCQs

Question 3. A planet moving along an elliptical orbit is closest to the sun at a distance of r₁ and farthest away at a distance of r₂. If V₁ and V₂ are the liner velocities at these points respectively, then the ratio \(\frac{v_1}{v_2}\) is:

1. \(\frac{r_2}{r_1}\)
2. \(\left(\frac{r_2}{r_1}\right)^2\)
3. \(\frac{r_1}{r_2}\)
4. \(\left(\frac{r_1}{r_2}\right)^2\)

Answer: 1. \(\frac{r_2}{r_1}\)

Using the law of conservation of angular moments \(m_1 v_1 =m_2 v_2 \)

⇒ \(m r_1 v_1 =m r_2 v_2 \)

⇒ \(r_1 v_1 =r_2 v_2 \)

∴ \(\frac{v_1}{v_2} =\frac{r_2}{r_1}\)

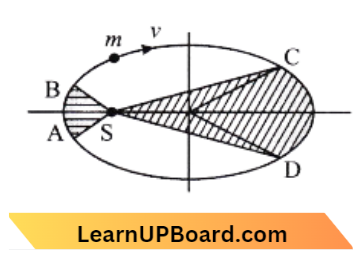
Question 4. The figure shows the elliptical orbit of a plant m about the sun S. The shaded area SCD is twice the shaded area SAB, if t₁ is the time for the planet to move from C to D and t₂ is the time to move from A to B, then:

1. \(t_1>t_2\)
2. \(t_1=4 t_2\)
3. \(t_1=2 t_2\)
4. \(t_1=t_2\)

Answer: 3. \(t_1=2 t_2\)

Applying Kepler’s law of planetary motion. \(\frac{d A}{d t}\) = constant

⇒ \(\frac{A_1}{t_1} =\frac{A_2}{t_2} \)

⇒ \( t_1 =\frac{A_1}{A_2} t_2 \)

Since, \(A_1 =2 A_2\)

Hence, \(t_1 =2 t_2\)

Question 5. The period of revolution of the planet A around the sun is 8 times that of B. The distance of A from the sun is how many times greater than that of B from the sun?

1. 5
2. 4
3. 3
4. 2

Answer: 2. 4

According to Kelper’s third law,

⇒ \(T^2 \propto r^3\)

Where, T= period of revolution

r= Semi-major axis

⇒ \(\frac{T_A^2}{T_B^2} =\frac{r_A^3}{r_B^3}\)

⇒ \( \frac{r_A}{r_B} =\left(\frac{T_A}{T_B}\right)^{2 / 3} \)

=\( (8)^{\frac{2}{3}}\)

=\(2^{3 \times \frac{2}{3}}\) =4

or \(r_A =4 r_B\)

Question 6. The distances of the two planets from the sun are 10¹³ and 10¹² m respectively. The ratio of periods of these two planets is:

1. \(\frac{1}{\sqrt{10}}\)
2. 100
3. 10 \(\sqrt{10}\)
4. 1 \(\sqrt{10}\)

Answer: 3. 10 \(\sqrt{10}\)

According to Kepler’s third law (or the law of periods) \(T^2 \propto r^3\)

Here, \(r_1=10^{13} \mathrm{~m}, r_2=10^{12} \mathrm{~m}\)

⇒ \(\frac{T_1^3}{T_2^2}=\frac{r_1^3}{r_2^3}=\frac{\left(10^{13}\right)^3}{\left(10^{12}\right)^3}\)

or \(\frac{T_1^2}{T_2^2}=\frac{10^{39}}{10^{36}}=10^3 \)

or \(\frac{T_1}{T_2}=10 \sqrt{10}\)

Question 7. A planet is moving in an elliptical orbit around the Sun. If. T, V, E and L stand respectively for their kinetic energy, gravitational potential energy, total energy and magnitude of angular momentum about the centre of force, which of the following is correct?

1. T is conserved.
2. V is always positive.
3. E is always negative.
4. T is conserved but the direction of vector L changes continuously.

Answer: 3. E is always negative.

In a circular or elliptical orbital motion of a planet, angular momentum is conserved. In an attractive field, potential energy and total energy are negative. Kinetic energy increases with an increase in velocity. If the motion is in a plane, the direction of L does not change.

Question 8. The largest and the shortest distance of the Earth from the sun are r₁ and r₂. Its distance from the sun when it is perpendicular to the major axis of the orbit drawn from the sun is

1. \(\frac{r_1+r_2}{4}\)
2. \(\frac{r_1+r_2}{r_1-r_2}\)
3. \(\frac{2 r_1 r_2}{r_1+r_2}\)
4. \(\frac{r_1+r_2}{3}\)

Answer: 3. \(\frac{2 r_1 r_2}{r_1+r_2}\)

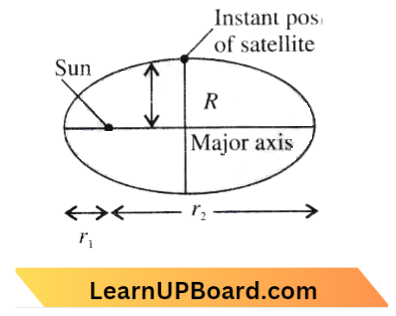
Applying the properties of ellipse,

we have, \(\frac{2}{R} =\frac{1}{r_1}+\frac{1}{r_2}\)

=\(\frac{r_1+r_2}{r_1 r_2}\)

∴ \(\mathrm{R} =\frac{2 r_1 r_2}{r_1+r_2}\)

Question 9. Two astronauts are floating in gravitation-free space after having lost contact with their spaceship. The two will:

1. keep floating at the same distance between them
2. move towards each other
3. move away from each other
4. will become stationary

Answer: 2. move towards each other

Both the astronauts are in the condition of weightless. The gravitational force between them pulls towards each other

Question 10. Kepler’s third law states that the square of the period of revolution (7) of a planet around the sun, is proportional to the third power of the average distance r between the sun and planet is T² = Kr³ here K is constant. If the masses of the sun and planet are M and m respectively, then as per Newton’s law of gravitation force of attraction between them is:\(\mathrm{F}=\frac{\mathrm{GM} m}{r^2}\), here G gravitational constant. The relation between G and K is described as:

1. \(\mathrm{GK}=4 \pi^2\)
2. \(\mathrm{GMK}=4 \pi^2\)
3. \(\mathrm{K}=\mathrm{G}\)
4. K=\(\frac{1}{G}\)

Answer: 2. \(\mathrm{GMK}=4 \pi^2\)

Let the mass of the Sun = M

and mass of planet = m

Then the gravitational force between them, \(\mathrm{F}=\frac{\mathrm{GM} m}{r^2}\)

\(\mathrm{F}=\frac{\mathrm{GM} m}{r^2}\)

where, r= distance between sun and planet.

The above force provided the centripetal force,

⇒ \(\frac{\mathrm{GM} m}{r^2}=\frac{m v^2}{2}\)

⇒ \(\sqrt{\frac{\mathrm{GM}}{r}}\)=v

We know that the period of a planet is,

T =\(\frac{2 \pi r}{v}\)

T =\(\frac{2 \pi r}{\sqrt{\frac{\mathrm{GM}}{r}}}\)

⇒ \(T^2=\frac{4 \pi^2 r^2}{\frac{\mathrm{GM}}{r}}=\frac{4 \pi^2 r^3}{\mathrm{GM}}\) → Equation 1

According to Kepler’s third law, \(T^2 \propto r^3 \)  →  Equation 2

⇒ \(T^2=k r^3 \)

From eq. (1) and (2),

⇒ \(\frac{4 \pi^2 r^3}{\mathrm{GM}} =k r^3 \)

∴ \(\mathrm{GMK} =4 \pi^2\)

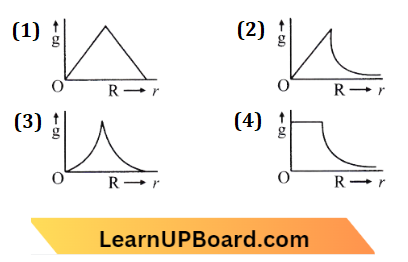
Question 11. The dependence of the intensity of gravitational field (E) of Earth distance (r) from the centre of Earth is correctly represented by:

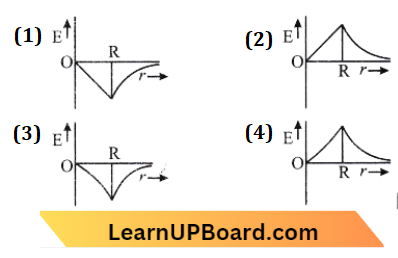
Answer: 2.

Option (B) is the graph of dependence of the intensity of gravitational field (E) of Earth with distance (r) from the centre of Earth

Question 12. Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of radius R (r is measured from the centre of the spherical shell)?

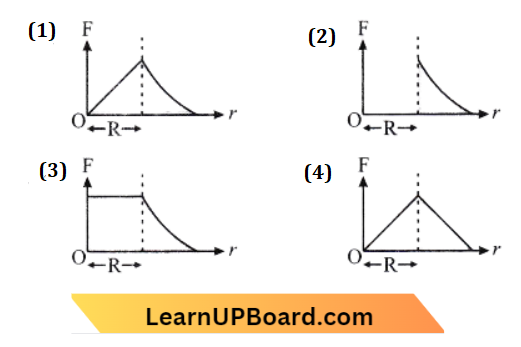
Answer: 2.

Question 13. A body projected vertically from the Earth reaches a height equal to the Earth’s radius before returning to the Earth. The power exerted by the gravitational force is greatest:

1. at the instant just before the body hits the Earth
2. it remains constant all through
3. at the instant just after the body is projected
4. at the height position of the body

Answer: 1. at the instant just before the body hits the Earth

We know that, P=\(\vec{F} \cdot \vec{v}=F v \cos \theta\)

Power will be maximum when velocity and \(cos \theta\) will be maximum.

Question 14. Two spheres of masses m and M are situated in the air and the gravitational force between them is F. The space around the masses is now filled with a liquid of specific gravity 3. The gravitational force will now be:

1. 3F
2. F
3. \(\frac{F}{3}\)
4. \(\frac{F}{9}\)

Answer: 2. F

The gravitational force does not depend upon the medium in which objects are placed.

Question 15. Gravitational force is required for:

1. stirring of liquid
2. convection
3. conduction
4. radiation

Answer: 2. convection

Fluid sections become lighter and flow upward as temperature rises, while heavier and denser fluid portions migrate lower. As a result, particles move up and down depending on their weight and gravity. As a result, the existence of a gravitational field is essential in natural convection heat transfer

Question 16. A body of weight 72 N moves from the surface of Earth at a height half of the radius of Earth, then the gravitational force exerted on it will be:

1. 36 N
2. 32 N
3. 144 N
4. 50 N

Answer: 2. 32 N

⇒ \(\mathrm{F}_{\text {surface }} =F \frac{M m}{R_e^2}\)

⇒ \(\mathrm{~F}_{R_e / 2} =G \frac{M m}{\left(R_e+R_e / 2\right)^2}\)

=\(\frac{4}{9} \times F_{\text {surface }}\)

=\(\frac{4}{9} \times 72=32 \mathrm{~N}\)

Question 17. Two particles of equal mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is:

1. \(\frac{1}{2} \sqrt{\frac{G m}{R}}\)
2. \(\sqrt{\frac{4 G m}{R}}\)
3. \(\frac{1}{2 R} \sqrt{\frac{1}{G m}}\)
4. \(\sqrt{\frac{G m}{R}}\)

Answer: 1. \(\frac{1}{2} \sqrt{\frac{G m}{R}}\)

Force between the two masses, F = \(-G \frac{m m}{4 R^2}\)

This force will provide the necessary centripetal force for the masses to go around a circle, then,

⇒ \(\frac{G m m}{4 R^2} =\frac{m v^2}{R}\)

⇒ \(v^2 =\frac{G m}{4 R}\)

v =\(\frac{1}{2} \sqrt{\frac{G m}{R}}\)

Question 18. The Earth (mass = 6 x 1024 kg) revolves around the sun with an angular velocity of 2 x 10^-7 rad/s in a circular orbit of radius 1.5 x 10⁸ km. The force exerted by the sun on the Earth, in Newton is:

1. 36 x 10²¹
2. 27 x 10³⁹
3. zero
4. 18 x 10²³

Answer: 1. 36 x 10²¹

Give: mass(m) =\(6 \times 10^{24} \mathrm{~kg}\)

angular velocity \((\omega) =2 \times 10^{-7} \mathrm{rad} / \mathrm{s}\) and

radius(r) =\(1.5 \times 10^8 \mathrm{~km}\)

=\(1.5 \times 10^{11} \mathrm{~m}\)

Force exerted on the Earth =\(\mathrm{mRw}^2\)

=\(\left(6 \times 10^{24}\right) \times\left(1.5 \times 10^{11}\right) \times\left(2 \times 10^{-7}\right)^2\)

=\(36 \times 10^{21} \mathrm{~N}\)

Question 19. If the gravitational force between two objects were proportional to 1 /R (and not as I /R²), where R is the distance between them, then a particle in a circular path (under such a force) would have its orbital speed v, proportional to:

1. R
2. R° (independent of R)
3. 1/R²
4. 1/R

Answer: 2. R° (independent of R)

Centripetal force (F)=\(\frac{m v^2}{R}\) and the gravitational force \((\mathrm{F})=\frac{G M m}{R}=\frac{G M m}{R}, (where R^2 \rightarrow R )\).

Since \(\frac{m v^2}{R}=\frac{G M m}{R}\) therefore v=\(\sqrt{G M}\).

Thus velocity v is independent of R.

Question 20. If the mass of the Earth were ten times smaller and the universal gravitational constant were ten times larger in magnitude, which of the following is not correct?

1. The period of a simple pendulum on the Earth would decrease
2. Walking on the ground would become more difficult
3. Raindrops will fall faster
4. ‘g’ on the Earth will not change

Answer: 1. The Period of a simple pendulum on the Earth would decrease

Let \(M_e\) =riginal mass of Earth

G =Gravitational constant

Then from question, Mass of Earth \(M_E^{\prime}=\frac{M_E}{10}\)

New gravitational constant \(G^{\prime}\)=10 G

We know that, Acceleration due to gravity,

g=\(\frac{G M_E}{R^2}\)

⇒ \(M_E\) = mass of Earth

R = radius of Earth

New acceleration due to gravity u,

⇒ \(g^{\prime} =\frac{G^{\prime} M_E}{R^2}\)

=\(\frac{10 M_E G}{R L}\)

⇒ \(g^{\prime} =10 \mathrm{~g}\)

We also know that time pursued by a simple pendulum is,

T=\(2 \pi \sqrt{\frac{1}{g}}\)

⇒ \(T \propto \sqrt{\frac{1}{g}}\)

∴ This confirms that the period of the pendulum also decreases with the increase in g.

Question 21. A spherical planet has a mass of M_P and a diameter of D_P. A particle of mass m falling freely near the surface of this planet will experience acceleration due to gravity is

1. \(\frac{\Delta G M_P}{D_P^2}\)
2. \(\frac{G M_p m}{D_P^2}\)
3. \(\frac{G M_P m}{D_P^2}\)
4. \(\frac{4 G M_P m}{D_P^2}\)

Answer: 1. \(\frac{\Delta G M_P}{D_P^2}\)

We know that, Gravitational Force, F =\(\frac{G M_e m}{R^2}\)

F =\(\frac{G M_P m}{\left(D_P / 2\right)}\)

=\(\frac{4 G M_P m}{D_P^2}\)

And, F=m a

a =\(\frac{F}{m}\)

=\(\frac{\Delta G M_P m}{P^2}\)

=\(\frac{\Delta G M_P}{\Delta p^2}\)

Question 22. Imagine a new planet having the same density as that of Earth but it is 3 times bigger than the Earth in size. If the acceleration due to gravity on the surface of Earth is g and that on the surface of the new planet is g’ then:

1. \(g^{\prime}=\frac{g}{9}\)
2. \(g^{\prime}\)=27 g
3. \(g^{\prime}\)=9 g
4. \(g^{\prime}\)=3 g

Answer: 4. \(g^{\prime}\)=3 g

g =\(\frac{G M}{R^2}=\frac{G \frac{4}{3} \pi R^2 \rho}{R^2}\)

=\(\frac{4}{3} G \pi R \rho\)

∴ \(g^{\prime} =\frac{4}{3} G \pi(3 R) \rho\) =3 g

Question 23. The density of a newly discovered plant is twice that of Earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the Earth. If the radius of the Earth is R, the radius of the planet would be:

1. 2R
2. 4R
3. \(\frac{1}{4} R\)
4. \(\frac{1}{2} R\)

Answer: 4. \(\frac{1}{2} R\)

We know that, \(\frac{G M_p}{R_p^2} =\frac{G M_e}{R_e^2}\)

⇒ \(\frac{G \times \frac{4}{3} \pi R_p^3 \rho_p}{R_p^2} =\frac{G \times \frac{4}{3} \pi R_e^3 \rho_e}{R_e^2}\)

we get, Given,

⇒ \(R_p \rho_p =R_e \rho_e \)

⇒ \(\rho_p =2 \rho_e\)

then \(R_p \times 2 \rho_e =R_e \rho_e\)

∴ \(R_p =\frac{R_e}{2}=\frac{R}{2}\)

Question 24. The acceleration due to gravity on planet A is 9 times the acceleration due to gravity on planet B. A man jumps to a height of 2 m on the surface of A. What is the height of the jump by the same person on the plane B?

1. 2/9 m
2. 18 m
3. 6 m
4. 2/3 m

Answer: 2. 18 m

Height Of Jump on the planet B

= \(\frac{g_A}{g_B} \times\)Height Of Jump on the planet A

= 2 x 9 = 18m

Question 25. What will be the formula of mass of the Earth in terms of g, R And G?

1. \(G \frac{R}{g}\)
2. \(g \frac{R^2}{G}\)
3. \(g^2 \frac{R}{G}\)
4. \(G \frac{g}{R}\)

Answer: 2. \(g \frac{R^2}{G}\)

As We Know, F =\(\frac{G M m}{R^2}\)

mg =\(\frac{G M m}{R^2}\)

g =\(\frac{G M}{R^2}\)

M =\(\frac{g R^2}{G}\)

Where, M = mass of earth

g = Gravitational Acceleration

R = Radius of Earth

G = Gravitational constant

Question 26. The acceleration due to gravity and mean density of the Earth \(rho\) are related by which of the following relations? (where G is the gravitational constant and R is the radius of the Earth.)

1. \(\rho=\frac{3 g}{4 \pi G R}\)
2. \(\rho=\frac{3 g}{4 \pi G R^3}\)
3. \(\rho=\frac{4 \pi g R^2}{3 G}\)
4. \(\rho=\frac{4 \pi g R^3}{3 G}\)

Answer: 1. \(\rho=\frac{3 g}{4 \pi G R}\)

Acceleration Due to Gravity g =\(G \times \frac{M}{R^2}\)

=G \(\frac{(4 / 3) \pi R^3 \times \rho}{R^2}\)

=G \(\times \frac{4}{3} \pi R \times \rho\)

or \(\rho =\frac{3 g}{4 \pi G R}\)

Question 27. The radius of Earth is about 6400 km and that of Mars is 3200 km. The mass of the Earth is about 10 times the mass of Mars. An object weighs 200 N on the surface of the Earth. Its weight on the surface of Mars will be:

1. 20 N
2. 8 N
3. 80 N
4. 40 N

Answer: 3. 80 N

Given: radius of Earth \(\left(R_e\right)\)=6400 \(\mathrm{~km}\); the radius of Mars \(\left(R_m\right)=3200 \mathrm{~km}\); the mass of Earth \(\left(M_e\right)=10 M_m\) and weight of the object on Earth \(/left(W_e)=200 \mathrm{~N}\).

⇒ \(\frac{W_m}{W_e} =\frac{m g_m}{m g_e}\)

=\(\frac{M_m}{M_e} \times\left(\frac{R_e}{R_m}\right)^2\)

=\(\frac{1}{10} \times(2)^2=\frac{2}{5}\)

∴ \(W_m=W_e \times \frac{2}{5}=200 \times 0.4=80 \mathrm{~N}\)

Question 28. A particle of mass ‘w’ is projected with a velocity v = kV_e (k < 1) from the surface of the Earth. (v_e = Escape velocity) The maximum height above the surface reached by the particle is

1. \(\mathrm{R}\left(\frac{\mathrm{K}}{1-k}\right)^2\)
2. \(\mathrm{R}\left(\frac{\mathrm{K}}{1+k}\right)^2\)
3. \(\frac{\mathrm{R}^2 k}{1+k}\)
4. \(\frac{\mathrm{R} k^2}{1-k^2}\)

Answer: 4. \(\frac{\mathrm{R} k^2}{1-k^2}\)

Given, v=\(\mathrm{K} v_e\), H =?

At max height H \(\mathrm{KE} =\mathrm{PE}\)

⇒ \(\mathrm{KE} =\frac{1}{2} m v^2\)

=\(\frac{1}{2} m \mathrm{~K}^2 \mathrm{~V}_e{ }^2 \)

⇒ \(\mathrm{PE} =\frac{\mathrm{GM} m}{\mathrm{R}+\mathrm{H}}\)

⇒ \(\mathrm{v}_e{ }^2 =\frac{2 \mathrm{GM}}{\mathrm{R}}\)

⇒ \(\frac{\mathrm{K}^2}{\mathrm{R}} =\frac{1}{\mathrm{R}+\mathrm{H}}\)

⇒ \(\mathrm{R}+\mathrm{H} =\frac{\mathrm{R}}{\mathrm{K}^2}\)

H =\(R\left(\frac{1}{\mathrm{~K}^2}-1\right)\)

=\(R\left(\frac{1-\mathrm{K}^2}{\mathrm{~K}^2}\right)\)

Question 29. The dependence of acceleration due to gravity g on the distance f from the centre of Earth assumed to be a sphere of radius R of uniform density is as shown in the figure below:

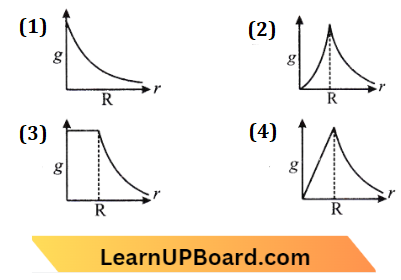
Answer: 4.

g \(\propto r(\text { if } r<R)\)

And \(\mathrm{g} \propto \frac{1}{r^2}(\text { If } r>R)\)

The correct figure is D.

Question 30. What is the depth at which the value of acceleration due to gravity becomes 1/n times the value at the surface of Earth (Radius of Earth = R)?

1. \(\frac{\mathrm{R}}{n^2}\)
2. \(\frac{\mathrm{R}(n-1)}{n}\)
3. \(\frac{\mathrm{Rn}}{(n-1)}\)
4. R.n

Answer: 2. \(\frac{\mathrm{R}(n-1)}{n}\)

Radius of Earth = R

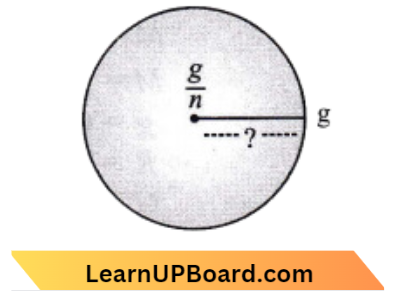
Let at depth d, gravitational acceleration become \(\frac{g}{n}\)

⇒ \(g_d =g_o\left(1-\frac{d}{R}\right)\)

⇒ \(\frac{g_o}{n} =g_o\left(1-\frac{d}{R}\right)\)

⇒ \(\frac{1}{n} =1-\frac{d}{R}\)

⇒ \(\frac{d}{R} =1-\frac{1}{n}\)

⇒ \(\frac{d}{R} =\left(\frac{n-1}{n}\right)\)

d =\(\left(\frac{n-1}{n}\right)\) R .

Question 31. A body weighs 72 N on the surface of the Earth. What is the gravitational force on it, at a height equal to half of the radius of the Earth?

1. 32N
2. 30N
3. 24N
4. 48N

Answer: 1. 32N

Given, W = mg = 72 N

On the surface of the Earth. At a height equal to half of the radius of Earth.h=\(\frac{\mathrm{R}}{2}\)

Acceleration due to gravity,

⇒ \(g^{\prime} =g\left(\frac{\mathrm{R}}{\mathrm{R}+h}\right)^2\)

= \(\mathrm{g}\left(\frac{\mathrm{R}}{\mathrm{R}+\frac{\mathrm{R}}{2}}\right)^2\)

= \(g\left(\frac{4 \mathrm{R}^2}{9 \mathrm{R}^2}\right)\)

⇒ \(g^{\prime} =g \times \frac{4}{9}\)

⇒ \(m g^{\prime} =m g \times \frac{4}{9}\)

= \(\frac{4}{9} \times 72 \)

∴ \(m g^{\prime} =32 \mathrm{~N}\)

Question 32. A body weighs 200 N on the surface of the Earth. How much will it weigh halfway down to the centre of the Earth?

1. 200N
2. 250N
3. 100N
4. 150N/kg

Answer: 3. 250N

Below the surface of Earth, acceleration due to gravity is: \(g^{\prime}=\left(1-\frac{d}{R}\right)\)   →   Equation 1

Where, d= depth, R: is the radius of Earth g = acceleration due to gravity Multiply m in both sides of the equations

⇒ \(Given, m g^{\prime}=m g\left(1-\frac{d}{R}\right)\)  →   Equation 2

Given, W=m g=200

d=\(\frac{R}{2}\)

Putting these values in eq. (2), we get

⇒ \(m g^{\prime} =200\left(1-\frac{R}{\frac{2}{R}}\right)=200\left(1-\frac{1}{2}\right)\)

=\(200 \times \frac{1}{2}\)

=100 N

∴ The body will weigh 100 N halfway down to the centre of Earth.

Question 33. The acceleration due to gravity at a height of 1 km above the Earth is the same as at a depth d below the surface of the Earth. Then:

1. d=\(\frac{1}{2} \mathrm{~km}\)
2. d=1 \(\mathrm{~km}\)
3. d=\(\frac{3}{2} \mathrm{~km}\)
4. d=2 \(\mathrm{~km}\)

Answer: 4. d=2 \(\mathrm{~km}\)

Given that acceleration due to gravity at depth d is,

⇒ \(g^{\prime}=g\left(1-\frac{d}{R}\right)\)  →  Equation 1

Where, R=radius of Earth

And Acceleration due to gravity at height h is,

⇒ \(g^{\prime \prime}=g\left(1-\frac{2 h}{R}\right)\)   →  Equation 2

According to question,\( g^{\prime} =g^{\prime \prime}\) and h=1 \(\mathrm{~km}\)

⇒ \(g\left(1-\frac{d}{R}\right) =g\left(1-\frac{2 h}{R}\right)\)

(putting h=1 )

⇒ \(g\left(1-\frac{d}{R}\right) =g\left(1-\frac{2}{R}\right)\)

⇒ \(\frac{d}{R} =\frac{2}{R}\)

d =2 km

Question 34. Starting from the centre of the Earth having radius R, the variation of due to gravity) is shown by:

Answer: 2.

We know that acceleration due to gravity below \(g_d=g\left(1-\frac{d}{R}\right)\)

and acceleration due to gravity at height h is \(g_h=g\left(\frac{R^2}{(R+h)^2}\right)\)

From the above equation, it is clear that the value of g increases from the centre of the maximum at the surface and then decreases

g=\(\left(\frac{G M_e}{R_e^3}\right) r, \text { for } 0<r \leq R_e\)

⇒ \(g \propto r \)

⇒ \(g=\frac{G M_e}{r^2}\), for \(r<R_e \)

∴ \(g \propto \frac{1}{r^2}\)

Question 35. The height at which the weight of a body becomes 1/16th its weight on the surface of Earth (radius R), is:

1. 5 R
2. 15 R
3. 3 R
4. 4 R

Answer: 3. 3 R

According to the question, \(\frac{G M \not m}{(R+h)^2}=\frac{1}{16} \frac{G M \not h}{R^2}\)

Where, R= Radius of Earth

⇒ \(\frac{1}{(\mathrm{R}+h)^2}=\frac{1}{16 R^2}\)

⇒ \(\frac{R}{R+h}=\frac{1}{4}\)

⇒ \(\frac{R+h}{R}\)=4

∴ h = 3R

Question 36. A body of mass 60 g experiences a gravitational force of 3.0 N when placed at a particular point. The magnitude of the gravitational field intensity at that point is:

1. 15 N/kg
2. 20N/kg
3. 150N/kg
4. 0.05 N/kg

Answer: 1. 15 N/kg

Given: Mass of the body, m= 60 g = 0.06 kg

Gravitational force, F =3.0 N

The gravitational field intensity is written as; \(I_g=\frac{F}{m}\) →  Equation 1

Now, On putting all the given values in equation (1) we have,

⇒ \(I_g=\frac{3.0}{0.06}\)

∴ \(I_g=50 \mathrm{~N} / \mathrm{kg}\)

Question 37. A particle of mass M is situated at the centre of a spherical shell of the same mass and radius a. ‘The magnitude of the gravitational potential at a point situated at \(\frac{a}{2}\) distance from the centre, will be:

1. \(\frac{2 G M}{a}\)
2. \(\frac{3 G M}{a}\)
3. \(\frac{4 G M}{a}\)
4. \(\frac{G M}{a}\)

Answer: 2. \(\frac{3 G M}{a}\)

⇒ \(v_P =v_{\text {sphere }}+v_{\text {particle }}\)

⇒ \(v_P =\frac{G Y}{a}+\frac{G Y}{a / 2} \)

=\(\frac{G Y}{a}+\frac{2 G y}{a}=\frac{3 G Y}{a}\)

Question 38. The work done to raise a mass m from the surface of the Earth to a height h, which is equal to the radius of the Earth, is:

1. \(\frac{3}{2} m g R\)
2. mgR
3. 2 \(\mathrm{mgR}\)
4. \(\frac{1}{2} m g R\)

Answer: 4. \(\frac{1}{2} m g R\)

Work done = Change in potential energy

=\(u_f-u_i=\frac{-G M m}{(R+h)}-\left(\frac{-G M m}{R}\right)\)

where, \(\mathrm{M}\) is the mass of Earth and \(\mathrm{R}\) is the radius of Earth.

⇒ \(\mathrm{W}=G M m\left[\frac{1}{R}-\frac{1}{(R+h)}\right]\)

Now, h=R

W=\(G M m\left[\frac{1}{R}-\frac{1}{2 R}\right]=\frac{G M m}{2 R}\)

W=\(\frac{m g R}{2} g=\frac{G M}{R^2}\)

Question 39. At what height from the surface of Earth are the gravitation potential and the value of g – 5.4 * 10⁷ J kg^-2 and 6.0 ms^-2 respectively? [Take, the radius of Earth as 6400 km.]

1. 1600 km
2. 1400 km
3. 2000 km
4. 2600 km

Answer: 4. 2600 km

We know that Gravitational potential at height h from the surface of Earth is v=\(-\frac{G M}{R+h}\)

Here, v=\(-\frac{G M}{R+h}=-5.4 \times 10^7\)  →  Equation 1

Given an acceleration due to gravity of height ft from the surface of Earth,

g=\(\frac{G M}{(R+h)^2}\)=6  →  Equation 2

Divide eq. (1) by eq. (2),

=\(\frac{5.4 \times 10^7}{(R+h)}\)=6

⇒ R+h=9000 km =9000-6400

h =2600 km

Question 40. An infinite number of bodies, each of mass 2 kg are situated on the x-axis at distances 1 m, 2 m, 4 m, and 8 m, respectively from the origin. The resulting gravitational potential due to this system at origin will be:

1. -G
2. \(-\frac{8}{3} G\)
3. \(-\frac{4}{3} G\)
4. -4 G

Answer: 4. -4 G

The resulting gravitational potential due to the system again is,

V =\(-2 G\left[1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\ldots\right]\)

=\(-2 G\left[1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\ldots\right]\)

V =\(-2 G\left(1-\frac{1}{2}\right)^{-1} \)

V =\(\frac{-2 G}{\left(1-\frac{1}{2}\right)}\)

V =\(\frac{-2 G}{\frac{1}{2}}\)=-4 G

V =-4 G

Question 41. A body of mass ‘m’ is taken from the Earth’s surface to a height equal to twice the radius (R) of the Earth. The change in potential energy of the body will be:

1. 3 mgR
2. \(\frac{1}{3} m g R\)
3. mg 2R
4. \(\frac{2}{3} m g R\)

Answer: 4. \(\frac{2}{3} m g R\)

Gravitational potential energy at any point at a distance r from the centre of the Earth is, U=\(-\frac{G M m}{r}\)

where M and m are masses of the Earth and the body respectively.

At the surface of the Earth, r =R ;

⇒ \(U_i =-\frac{G M m}{R}\)

At a height of h from the surface,

r=R+h=R+2 R=3 R

h = 2R (Given)

⇒ \(U_f =-\frac{G M m}{3 R}\)

Change in potential energy,

⇒ \(\Delta U =U_f-U_i\)

=\(-\frac{G M m}{3 R}-\left(-\frac{G M m}{R}\right)\)

=\(\frac{G M m}{R}\left(1-\frac{1}{3}\right)\)

=\(\frac{2}{3} \frac{G M m}{R}=\frac{2}{3} m g R\)

∴ \((g=\frac{G M}{R^2}\)

Question 42. A body of mass m is placed on Earth’s surface which is taken from Earth’s surface to a height of h = 3R, then the change in the gravitational potential energy is:

1. \(\frac{m g R}{4}\)
2. \(\frac{2}{3} m g R\)
3. \(\frac{3}{4} m g R\)
4. \(\frac{m g R}{2}\)

Answer: 3. \(\frac{3}{4} m g R\)

change in Gravitational Potential energy

= final energy – initial energy

=\(-\frac{G M m}{4 R}+\frac{\mathrm{G} M m}{R}\)

=\(-\frac{G M m}{4 R}\left[1-\frac{1}{4}\right]\)

=\(\frac{3}{4} \frac{G M m}{4 R}\)

=\(\frac{3}{4} \frac{G M}{R^2} m R=\frac{3}{4} g m R\)

Question 43. A particle of mass m is thrown upwards from the surface of the Earth, with a velocity u. The mass and the radius of the Earth are, respectively, M and R. G is gravitational contact and g is acceleration due to gravity on the the surface of the Earth. The minimum value of u so that the particle does not return to Earth, is:

1. \(\sqrt{\frac{2 G M}{R}}\)
2. \(\sqrt{\frac{2 G M}{R^2}}\)
3. \(\sqrt{2 g R^2}\)
4. \(\sqrt{\frac{2 G M}{R^2}}\)

Answer: 1. \(\sqrt{\frac{2 G M}{R}}\)

We know that Escape velocity, \(v_e=\sqrt{2 g R}\)

since, GM =\(9 \mathrm{R}^2 \)

=\(\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}^2} \times \mathrm{R}}=\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}}}\)

Question 44. The ratio of escape velocity on Earth (v_e) to the escape velocity at a planet (v_p) whose radius and mean density are twice that of Earth is:

1. 1: 2 \(\sqrt{2}\)
2. 1: 4
3. 1: \(\sqrt{2}\)
4. 1: 2

Answer: 1. 1: 2 \(\sqrt{2}\)

Since, escape velocity, \(v_e =\sqrt{\frac{2 G M}{R}}=\sqrt{\frac{2 G}{R}\left(\frac{4}{3} \pi R^3 \rho\right)}\)

⇒ \(v_e =R \sqrt{\rho}\)

∴ Ratio =\(1: 2 \sqrt{2}\)

Question 45. A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would Earth (mass = 5.98 x 10²⁴ kg) have to be compressed to be a black hole?

1. 10^-9 m
2. 10^-6 m
3. 10^-2 m
4. 100 m

Answer: 3. 10^-2 m

In this question compare escape relatives with the velocity of light c.

Escape velocity \(v_e=\sqrt{\frac{2 G M}{R}}\)

R= New radius of the Earth

Since,\( v_e=c\)

c=\(\sqrt{\frac{2 G M}{R}}\)

⇒ \(c^2=2 \frac{G M}{R}\)

R =\(\frac{2 G M}{c^2}\)

=\(\frac{2 \times 6.07 \times 10^{-11} \times 6 \times 10^{24}}{\left(3 \times 10^8\right)^2}\)

=\(\frac{2 \times 6.07 \times 10^{-11} \times 6 \times 10^{24}}{9 \times 10^{16}}\)

=\(\frac{4 \times 6.07}{3} \times 10^{-3}\)

=0.889 \(\times 10^{-2}\)

⇒ \(10^{-2} \mathrm{~m}\)

Here, gravitational constant G=\(6.07 \times 10^{-11}\)

Mass of Earth M=\(6 \times 10^{14} \mathrm{~kg}\)

Question 46. The radius of the planet is twice the radius of Earth. Both have almost equal average mass densities v_p and v_E are escape velocities of the planet and the Earth respectively, then:

1. v_p = 1.5 v_E
2. v_p = 2 v_E
3. v_E= 3 v_p
4. v_E= 1.5 v_p

Answer: 2. v_p = 2 v_E

According to the question,

⇒ \(R_P=2 R_E, \rho_E=\rho_P\)

Escape velocity of Earth, \(v_E =\sqrt{\frac{2 G M_E}{R_E}}\)

=\(\sqrt{\frac{2 G}{R_E}\left(\frac{4}{3} \pi R_E{ }^3 \rho_E\right)}\)

=\(R_E \sqrt{\frac{8}{3} \pi G \rho_E}\)  → Equation 1

Similarly, the Escape velocity of the planet

⇒ \(v_P=\sqrt{\frac{2 G M_P}{R_P}}\)

⇒ \(v_P=\sqrt{\frac{2 G}{R_P}\left(\frac{4}{3} \pi R_p^3 \rho_p\right)}\)

⇒ \(v_P=R_P \sqrt{\frac{8}{3} \pi G \rho_p}\)  →  Equation 2

from eq. (1) and eq. (2), we get,

⇒ \(\frac{v_E}{v_P} =\frac{R_E}{R_P} \sqrt{\frac{\rho_E}{\rho_P}}\)

=\(\frac{R_E}{2 R_E} \sqrt{\frac{\rho_Q}{\rho_E}}=\frac{1}{2}\)

∴ \(v_p =2 v_E\)

Question 47. A particle of mass W is kept at rest at a height 3R from the surface of Earth, where ‘R’ is the radius of Earth and ‘M is the mass of Earth. The minimum speed with which it should be projected, so that it does not return, is (g is the acceleration due to gravity on the surface of Earth):

1. \(\left(\frac{G M}{2 R}\right)^{\frac{1}{2}}\)
2. \(\left(\frac{g R}{4}\right)^{\frac{1}{2}}\)
3. \(\left(\frac{2 g}{R}\right)^{\frac{1}{2}}\)
4. \(\left(\frac{G M}{R}\right)^{\frac{1}{2}}\)

Answer: 1. \(\left(\frac{G M}{2 R}\right)^{\frac{1}{2}}\)

Escape velocity \(v_e=\sqrt{\frac{2 \mathrm{GM}}{(\mathrm{R}+h)}}\)

From the question h=3 R

⇒ \(v_e^{\prime} =\sqrt{\frac{2 \mathrm{GM}}{\mathrm{R}+3 \mathrm{R}}}\)

=\(\sqrt{\frac{2 G M}{4 R}}\)

=\(\sqrt{\frac{G M}{2 R}}=\sqrt{\frac{g R}{2}}\)

∴ where, g =\(\frac{G M}{R^2}\)

Question 48. The Earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of the Earth. The escape velocity of a body from this platform is fv, where v is its escape velocity from the surface of the Earth. The value of f is:

1. \(\frac{1}{2}\)
2. \(\sqrt{2}\)
3. \(\frac{1}{\sqrt{2}}\)
4. \(\frac{1}{3}\)

Answer: 3. \(\frac{1}{\sqrt{2}}\)

We know that Escape velocity,

⇒ \(v_e=\sqrt{2 g R}\)

Escape velocity of the body from the platform,

⇒ \(\mathrm{P} \cdot \mathrm{E}+\mathrm{K} \cdot \mathrm{E}\) =0

⇒ \(-\frac{G M m}{2 R}+\frac{1}{2} m v^2\) =0

v =\(\sqrt{\frac{G M}{R^2}+R}=\sqrt{g R}\)

This confirms that:

fv =\(\frac{v}{\sqrt{2}}\)

f =\(\frac{1}{\sqrt{2}}\)

Question 49. Which velocity should a particle be projected so that its height becomes equal to the radius of Earth?

1. \(\left(\frac{G M}{R}\right)^{1 / 2}\)
2. \(\left(\frac{8 G M}{R}\right)^{1 / 2}\)
3. \(\left(\frac{2 G M}{R}\right)^{1 / 2}\)
4. \(\left(\frac{4 G M}{R}\right)^{1 / 2}\)

Answer: 1. \(\left(\frac{G M}{R}\right)^{1 / 2}\)

Use , \(v^2=\frac{2 g n}{1+\frac{h}{R}}\) given h= R

v=\(\sqrt{g R}=\sqrt{\frac{G M}{R}}\)

Question 50. For a planet having mass equal to the mass of the Earth the radius is one-fourth of the radius of the Earth. The escape velocity for this planet will be :

1. 11.2 km/s
2. 22.4 km/s
3. 5.6 km/s
4. 44.8 km/s

Answer: 2. 22.4 km/s

⇒ \(v_e =\sqrt{2 g R_e}=\sqrt{\frac{2 G M}{R_e}}\)

⇒ \(R_p =\frac{1}{4} R_e\)

∴ \(v_p =2 v_e=2 \times 11.2=22.4 \mathrm{~km} / \mathrm{s}\)

Question 51. The escape velocity of a sphere of mass m is given by (G = Universal gravitational constant; M_e = Mass of the earth and R_e = Radius of the earth)₁

1. \(\sqrt{\frac{2 G M_e m}{R_e}}\)
2. \(\sqrt{\frac{2 G M_e}{R_e}}\)
3. \(\sqrt{\frac{G M_e}{R_e}}\)
4. \(\sqrt{\frac{2 G M_e+R_e}{R_e}}\)

Answer: 2. \(\sqrt{\frac{2 G M_e}{R_e}}\)

To escape Earth’s gravitational pull and reach infinity, the starting kinetic energy must be somewhat more than the gravitational potential energy of the body on the surface.

The total energy of the body just after projecting is: \(\mathrm{E}=\frac{1}{2} m v^2-\frac{G M_e m}{R_e}\)

This total energy must now be slightly greater than zero for the minimum speed to be achieved when kinetic energy equals gravitational potential energy.

⇒ \(\frac{1}{2} m v^2 =\frac{G M_e m}{R_e}\)

⇒ \(\frac{1}{2} v^2 =\frac{G M_e}{R_e}\)

v =\(\sqrt{\frac{2 G M_e}{R_e}}\)

Question 52. The escape velocity of a body on the surface of the Earth is 11.2 km/s. If the Earth’s mass increases to twice its present value and the radius of the Earth becomes half, the escape velocity becomes:

1. 22.4 km/s
2. 44.8 km/s
3. 5.6 km/s
4. 11.2 km/s

Answer: 1. 22.4 km/s

Escape velocity of a body \(\left(v_e\right)=11.2 \mathrm{~km} / \mathrm{s}\);

New mass of the Earth \(M_e^{\prime}=2 M_e \) and the new radius of the Earth \(R_e^{\prime}=0.5 R_e\)

Escape velocity \(\left(v_e\right)=\sqrt{\frac{2 G M_e}{R_e}} \propto \sqrt{\frac{M_e}{R_e}}\)

⇒ \(\frac{v_e}{v_e^{\prime}} =\sqrt{\frac{M_e}{R_e} \times \frac{0.5 R_e}{2 M_e}}\)=\(\sqrt{\frac{1}{4}}=\frac{1}{2}\)

∴ \(v_e^{\prime} =2 v_e=22.4 \mathrm{~km} / \mathrm{s}\)

Question 53. The escape velocity from the Earth is 11.2 km/s. If a body is to be projected in a direction making an angle of 45° to the vertical, then the escape velocity is :

1. 11.2×2 km/s
2. 11.2 km/s
3. \(\frac{11.2}{\sqrt{2}} \mathrm{~km} / \mathrm{s}\)
4. \(11.2 \sqrt{2} \mathrm{~km} / \mathrm{s}\)

Answer: 2. 11.2 km/s

As, \(v_e=\sqrt{2 g R}=\sqrt{\frac{2 G M}{R}}\)

Hence, escape velocity does not depend on the angle of projection. Escape velocity will remain the same.

Hence, the escape velocity is 11.2 Km/s.

Question 54. For a satellite escape velocity is 11 km/s. If the satellite is launched at an angle of 60° with the vertical, then the escape velocity will be

1. \(11 \mathrm{~km} / \mathrm{s}\)
2. \(11 \sqrt{3} \mathrm{~km} / \mathrm{s}\)
3. \(\frac{11}{\sqrt{3}} \mathrm{~km} / \mathrm{s}\)
4. \(33 \mathrm{~km} / \mathrm{s}\)

Answer: 3. \(\frac{11}{\sqrt{3}} \mathrm{~km} / \mathrm{s}\)

Escape velocity on Earth is the minimum velocity with which the body has to be projected vertically upwards from the surface of the Earth. So, that it just crosses the gravitational field of Earth and never returns on its own. The escape velocity of the Earth is given by

⇒ \(v_e =\sqrt{\frac{2 G M}{R}}=\sqrt{2 g R}\)

=\(\sqrt{\frac{8 \pi \rho G R^2}{3}}\)

It is clear from the above equation that the value of a body’s escape velocity is independent of its mass (m) and angle of projection from the planet’s surface. As a result, the escape velocity remains unchanged. Hence, v = 11 km/s Projected velocity.

Question 55. The escape velocity from the Earth’s surface is v. The escape velocity from the surface of another planet having a radius, four times that of Earth and the same mass density is:

1. v
2. 2v
3. 3v
4. 4v

Answer: 2. 2v

Given the escape velocity of Earth = v

Radius of other planet = \(4 \mathrm{R}_e\)

Mass density is same = d

Mass of other planet =\(\frac{4}{3} \pi\left(4 \mathrm{R}_{\mathrm{e}}\right)^3 \cdot d \)

Mass of Earth =\(\frac{4}{3} \pi \mathrm{R}_{\mathrm{e}}^3 \cdot d \)

⇒ \(\mathrm{M}=\frac{\mathrm{M}_{\mathrm{P}}}{\mathrm{M}_e}=\frac{64 \mathrm{R}_e^3}{\mathrm{R}_e^3}\)=64

⇒ \(\mathrm{M}_P=64 \mathrm{M}_{\mathrm{e}}\)

We know, \(v_e=\sqrt{\frac{2 \mathrm{GM}_e}{\mathrm{R}_e}}\)

⇒ \(v_P=\sqrt{\frac{2 \mathrm{G}\left(64 \mathrm{M}_e\right)}{4 \mathrm{R}_e}}\)

=\(4 \sqrt{\frac{2 \mathrm{GM}_e}{\mathrm{R}_e}}\)

⇒ \(\frac{v_P}{v_e}\)=4

∴ \(v_P=4 v_e \)

Question 56. The period of a geostationary satellite is 24 h, at a height of 6RE (R_E is the radius of Earth) from the surface of Earth. The period of another satellite whose height is 2.5 R_E from the surface will be:

1. \(6 \sqrt{2} h\)
2. \(12 \sqrt{2} h\)
3. \(\frac{24}{2.5} h\)
4. \(\frac{12}{2.5} h\)

Answer: 1. \(6 \sqrt{2} h\)

From Kepler’s third law we know that period:

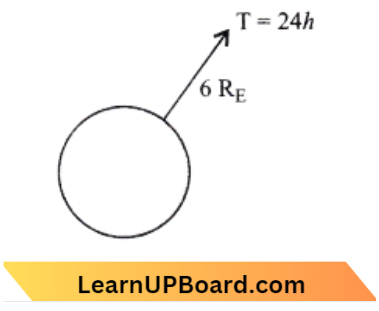
⇒ \(\mathrm{T}^2 \propto r^3\)

⇒ \(\mathrm{~T} =\sqrt[2]{r^3}\)  →  Equation 1

Where, r= radius of satellite’s orbit

Now from question, \(r_1=6 \mathrm{R}_{\mathrm{E}}+\mathrm{R}_{\mathrm{E}}, \mathrm{T}_1=24 \mathrm{~h}\)

⇒ \(r_2=2.5 \mathrm{R}_{\mathrm{E}}+\mathrm{R}_{\mathrm{E}}, \mathrm{T}_2\)=?

From eq. (1) we can write,

⇒ \(\left(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right)=\left(\frac{r_1}{r_2}\right)^{3 / 2}\)

Putting the given values,

⇒ \(\frac{24}{\mathrm{~T}_2} =\left(\frac{6 \mathrm{R}_{\mathrm{E}} 7 \mathrm{R}_{\mathrm{E}}}{2.5 \mathrm{R}_{\mathrm{E}} 7 \mathrm{R}_{\mathrm{E}}}\right)^{3 / 2}=\left(\frac{7 \mathrm{R}_{\mathrm{E}}}{3.5 \mathrm{R}_{\mathrm{E}}}\right)^{3 / 2}\)

=\(\left(\frac{7}{3.5}\right)^{3 / 2}=(2)^{3 / 2}\)

⇒ \(\mathrm{T}_2 =\frac{24}{(2)^{3 / 2}}\)

=\(\frac{24}{2 \sqrt{2}}=6 \sqrt{2} h\)

Question 57. A remote sensing satellite of Earth revolves in a circular orbit at a height of 0.25 x 10⁶ m above the surface of Earth. If Earth’s radius is 6.38 x 10⁶ m and g = 9.8 ms^-2, then the orbital speed of the satellite is:

1. 7.76 km^-1
2. 8.56 km^-1
3. 9.13 km^-1
4. 6.67 km^-1

Answer: 1. 7.76 km^-1

According to question, Height of a satellite, h=\(0.25 \times 10^6 \mathrm{~m}\)

Radius of Earth, \(R_E=6.38 \times 10^6 \mathrm{~m}\)

For the satellite revolving around the Earth

⇒ \(v_0=\sqrt{\frac{G M_E}{R_E}}=\sqrt{\frac{G M_E}{R_E\left[1+\frac{h}{R_E}\right]}}\)

=\(\sqrt{\frac{g R_E}{1+\frac{h}{R_E}}}\)

Putting value, \(v_0 =\sqrt{\frac{9.8 \times 6.38 \times 10^6}{1+\frac{0.25 \times 10^6}{6.38 \times 10^6}}}=\sqrt{60 \times 10^6}\)

=\(7.76 \times 10^3 \mathrm{~ms}^{-1}=7.76 \mathrm{~km} / \mathrm{s}\)

Question 58. A satellite S is moving in an elliptical orbit around the Earth. The mass of the satellite is very small compared to the mass of the Earth. Then:

1. the angular momentum of S about the centre of the Earth changes in direction, but its magnitude remains constant
2. the total mechanical energy of S varies periodically with time
3. the linear momentum of S remains constant in magnitude
4. the acceleration of S is always directed towards the centre of the Earth

Answer: 4. the acceleration of S is always directed towards the centre of the Earth

The mass of satellites is very small. The Centre of mass of the system coincides with the centre of the Earth

Question 59. A geostationary satellite is orbiting the Earth at a height of 5R above the surface of the Earth, R being the radius of the Earth. The period of another satellite in hours at a height of 2R from the surface of the Earth is:

1. 5
2. 10
3. \(6 \sqrt{2}\)
4. \(\frac{6}{\sqrt{2}}\)

Answer: 3. \(6 \sqrt{2}\)

Using Kepler’s third law as \(\mathrm{T}^2 \propto r^3\)

⇒ \(T_1^2 \propto r_1^3 \) and \( T_2^2 \propto r_2^3\)

⇒ \(\frac{T_2^2}{T_1^2}=\frac{r_2^3}{r_1^3}=\frac{(3 R)^3}{(6 R)^3}=\frac{1}{8}\)

⇒ \(T_2^2=\frac{1}{8} T_1^2\)

∴ \(T_S=\frac{24}{2 \sqrt{2}}=6 \sqrt{2} h\)

Question 60. If \(v_e\) is escaping velocity and \(v_0\) is the orbital velocity of a satellite for orbit close to Each surface, then these are related by:

1. \(v_0=\sqrt{2} v_e\)
2. \(v_0=v_e\)
3. \(v_e=\sqrt{2} v_0\)
4. \(v_e=\sqrt{2} v_0\)

Answer: 3. \(v_e=\sqrt{2} v_0\)

From the question, \(v_{\text {escape }}=\sqrt{\frac{2 G M}{R}}=v_e\)

⇒ \(v_{\text {orbital }}=\sqrt{\frac{G M}{R}}=v_0\)

From the above equations,

∴ \(v_e=\sqrt{2} v_0\)

Question 61. The radii of the circular orbits of two satellites A and B of the Earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be:

1. 3v/4
2. 6 v
3. 12v
4. 3v/2

Answer: 2. 6 v

According to the question,

Radius of satellite A = 4R

and radius of satellite B = R

Speed of satellite A = 3v

Speed of satellite B =?

We know that orbital velocity of satellite is, v =\(\sqrt{\frac{G M}{r}}\)

⇒ \(\frac{v_A}{v_B} =\sqrt{\frac{r_{\mathrm{B}}}{r_{\mathrm{A}}}}\)

=\(\sqrt{\frac{R}{4 R}}=\frac{1}{2}=\frac{3 v}{v_B}\)

∴ \(v_B =6 v\)

Question 62. A ball is dropped from a spacecraft revolving around the Earth at a height of 120 km. What will happen to the ball?

1. it will fall to the Earth gradually
2. it will go very far in the space
3. it will continue to move with the same speed along the original orbit of the spacecraft
4. it will move with the same speed, tangentially to the spacecraft

Answer: 3. it will continue to move with the same speed along the original orbit of the spacecraft

Since no external torque is applied therefore according to the law of conservation of angular momentum, the ball will continue to move with the same angular velocity along the original orbit of the spacecraft.

Question 63. The escape velocity from the surface of the Earth is \(v_e\). The escape velocity from the surface of a planet whose mass and radius are three times those of the Earth will be:

1. \(v_e\)
2. \(3 v_e\)
3. \(9 v_e\)
4. \(\frac{1}{3 v_{\mathrm{e}}}\)

Answer: 1. \(v_e\)

Escape velocity on the surface of the Earth is given by

⇒ \(v_e =\sqrt{2 g R_{\mathrm{e}}}\)

=\(\sqrt{\frac{2 G M_{\mathrm{e}}}{R_{\mathrm{e}}}}  g=\frac{G M_{\mathrm{e}}}{R_e^2}\)

where, \(M_e\)= mass of Earth

⇒\(R_{\mathrm{e}}\)= radius of the Earth

G= gravitational constant

⇒ \(v_{\mathrm{e}} \propto \sqrt{\frac{M_{\mathrm{e}}}{R_{\mathrm{e}}}}\)

If \(v_p\) is escape velocity from the surface of the planet, then,

⇒ \(\frac{v_e}{v_p}=\sqrt{\frac{M_e}{R_e}} \times \sqrt{\frac{R_P}{M_P}}\)

where, \(M_p\) is mass of the planet and \(R_p\) is radius of the planet.

but \(R_p=3 R_e\) { (given) }

and \(M_p=3 M_e\)

⇒ \(\frac{v_e}{v_p} =\sqrt{\frac{M_e}{R_e}} \times \sqrt{\frac{3 R_e}{3 M_e}}\)

=\(\frac{1}{1}\)

or \(v_p=v_e\)

Question 64. A satellite I of mass m is at a distance r from the surface of the Earth. Another satellite B of mass 2 z is at a distance of 2 r from the Earth’s surface. Their periods are in the ratio of

1. 1:2
2. 1:16
3. 1:32
4. \(1: 2 \sqrt{2}\)

Answer: 4. \(1: 2 \sqrt{2}\)

According to Kepler’s third law, the square of the period of revolution of a planet around the sun is directly proportional to the cube of the major- axis of its elliptical orbit i.e. \( T^2 \alpha r^3\)

where T= time taken by the planet to go once around the sun.

r= semi-major axis of the elliptical orbit

⇒ \(\frac{T_1^2}{T_2^2}=\frac{(r)^3}{(2 r)^3}=\frac{1}{8}\)

∴ \(\frac{T_1}{T_2}=\frac{1}{2 \sqrt{2}}\)

Question 65. The additional kinetic energy to be provided to a satellite of mass ia revolving around a planet of mass M, to transfer it from a circular orbit of radius \(R_1\) to another of radius \(R_2\left(R_2>R_1\right)\) is:

1. \(G m M\left(\frac{1}{R_1^2}-\frac{1}{R_2^2}\right)\)
2. \(G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
3. \(2 G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
4. \(\frac{1}{2} G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

Answer: 4. \(\frac{1}{2} G m M\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)

The kinetic energy of the orbit of the satellite,

K E =\(\frac{\mathrm{GM} m}{2 \mathrm{R}_1}+\left(-\frac{\mathrm{GMm}}{2 \mathrm{R}_2}\right)\)

=\(\frac{\mathrm{GM} m}{2}\left[\frac{1}{\mathrm{R}_1}-\frac{1}{\mathrm{R}_2}\right]\)

Question 66. Assuming that the gravitational potential energy of an object at infinity is zero, the change in potential energy (final-initial) of an object of mass ru when taken to a height ft from the surface of Earth (of radius R) is given by:

1. \(\frac{G M m}{R+h}\)
2. \(\frac{G M m h}{R(R+h)}\)
3. mg
4. \(\frac{G M m}{R+h}\)

Answer: 2. \(\frac{G M m h}{R(R+h)}\)

⇒ \({ P.E. })_{\mathrm{A}} =-\frac{G M m}{R}\)

⇒ \({ P.E. })_{\mathrm{B}} =-\frac{G M m}{R+h}\)

⇒ \(\Delta U =(\mathrm{P} . \mathrm{E})_{\mathrm{B}}-(\mathrm{P} . \mathrm{E})_{\mathrm{A}}\)

=\(\frac{G M m}{R+h}+\frac{G M m}{R}\)

=\(\frac{G M m h}{R(R+h)}\)

Question 67. A satellite of mass z is orbiting the Earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of g₀, the value of acceleration due to gravity at the Earth’s surface is:

1. \(\frac{m g_0 \mathrm{R}^2}{2(\mathrm{R}+h)}\)
2. \(-\frac{m g_0 \mathrm{R}^2}{2(\mathrm{R}+h)}\)
3. \(\frac{2 m g_0 \mathrm{R}^2}{\mathrm{R}+h}\)
4. \(-\frac{2 m g_0 \mathrm{R}^2}{\mathrm{R}+h}\)

Answer: 2. \(-\frac{m g_0 \mathrm{R}^2}{2(\mathrm{R}+h)}\)

Total energy =K.E +P.K.

=\(\frac{G M m}{2(R+h)}-\frac{G M m}{(R+h)}\)

=\(\frac{-G M m}{2(R+h)}-\frac{G M m}{(R+h)}\)

=\(\frac{-m g^{\prime} R^2}{2(R+h)}\)

∴ \(\left(\text { where, } g^{\prime}\right.\left.=\frac{G M}{R^2}\right)\)

Question 68. Two satellites of Earth, S₁ and S₂ are moving in the same orbit. The mass of S₁ of four times the mass of S₂. Which one of the following statements is true?

1. The potential energies of Earth and satellite in the two cases are equal.
2. S₁ and S₂ are moving at the same speed
3. The kinetic energies of the two satellites are equal
4. The period of S₁ is four times that of S₂.

Answer: 2. S₁ and S₂ are moving at the same speed

⇒ \({K.E.}=\frac{G M m}{2 r}\)

Kinetic energies are unequal,

⇒ \(\mathrm{T}=\frac{2 \pi r^{3 / 2}}{\sqrt{G M}}\)

Periods are equal,

⇒ \({ P.E. }=-\frac{G M m}{r}\)

Potential energies are unequal,

V=\(\sqrt{\frac{G M}{r}}\)

orbital speeds are equal.

Question 69. For a satellite in an orbit around the Earth, the ratio of kinetic, energy to potential energy is:

1. \(\frac{1}{2}\)
2. \(\frac{1}{\sqrt{2}}\)
3. 2
4. \(\sqrt{2}\)

Answer: 1. \(\frac{1}{2}\)

⇒ \(-\frac{\mathrm{GMm}}{R^2}+m \omega^2 R \)=0

⇒ \(\frac{\mathrm{GMm}}{R^2} =m \omega^2 R\)

K.E. \( =\frac{1}{2} I \omega^2\)

=\(\frac{1}{2} m R^2 \omega^2\)

=\(\frac{\mathrm{GMm}}{2 R}\)

P.E =\(-\frac{\mathrm{GMm}}{R}\)

K.E =\(\frac{|P \cdot E|}{2}\)

∴ \(\frac{K . E}{P. E} =\frac{1}{2}\)

Question 70. The satellite of mass m is orbiting around the Earth in a circular orbit with a velocity v. What will be its total energy?

1. \((3 / 4) m v^2\)
2. \((1 / 2) m v^2\)
3. \(m v^2\)
4. \(-(1 / 2) m v^2\)

Answer: 4. \(-(1 / 2) m v^2\)

⇒ \({ K.E. of sattelite }=\frac{1}{2} m v^2\)

⇒ \({ (where, } v=\sqrt{\frac{G M}{r^2}}\)

P.E. of sattelite =\(\frac{G M m}{r}=-m v^2 \)

Total Energy = K. E. + P. E.

=\(\frac{1}{2} m v^2-m v^2=-\frac{1}{2} m v^2\)

Question 71. The mean radius of Earth is R, its angular speed on its axis is o and the acceleration due to gravity at Earth’s surface is g. What will be the radius of the orbit of a geostationary satellite?

1. \(\left(R^2 g / \omega^2\right)^{1 / 3}\)
2. \(\left(R g / \omega^2\right)^{1 / 3}\)
3. \(\left(R^2 \omega^2 / g\right)^{1 / 3}\)
4. \(\left(R^2 g / \omega\right)^{1 / 3}\)

Answer: 1. \(\left(R^2 g / \omega^2\right)^{1 / 3}\)

⇒ \(\frac{G M m}{r^2} =m \omega^2 r\)

\(r^3 =\frac{G M}{\omega^2}=\frac{g R^2}{\omega^2}\)

r =\(\left(g R^2 / \omega^2\right)^{1 / 3}\)