Kinetic Theory MCQs for NEET

Kinetic Theory

Question 1. The volume occupied by the molecules contained 4.5 kg water at STP, if the intermolecular forces vanish away is:

1. 5.6 x 10⁶ m³
2. 5.6 x 10³ m³
3. 5.6 x 10^-3m³
4. 5.6 m³

Answer: 4. 5.6 m³

At STP, \(\mathrm{T}=273 \mathrm{~K}, \mathrm{P}=10^5 \mathrm{~N} / \mathrm{m}^2\)

Number of moles of water,\(\mathrm{n} =\frac{\text { mass of water }}{\text { molecular weight of water }}\)

= \(\frac{4.5}{1.8 \times 10^{-2}}\)=250

Using equation, \(\mathrm{PV}=\mathrm{nRT}\)

= \(\frac{\mathrm{nRT}}{\mathrm{P}}=\frac{250 \times 8.3 \times 273}{10^5}\)

= \(5.6 \mathrm{~m}^3\)

Question 2. A given sample of an ideal gas occupies a volume V at a pressure P and absolute temperature T. The mass of each molecule of the gas is m. Which of the following gives the density of the gas?

1. \(\frac{P}{(k T)}\)
2. \(\frac{P m}{(k T)}\)
3. \(\frac{P}{(k T V)}\)
4. mkT

Answer: 2. \(\frac{P m}{(k T)}\)

If, m = mass of gas

v = Volume of gas

⇒ \(\rho=\frac{m}{V}\)= Density of gas

Pressure P =\(\frac{1}{2} \rho V_{\text {rms }}^2\)

= \(\frac{1}{3} \rho \frac{3 R T}{M_0}=\frac{\rho R T}{M_0}\)

⇒ \(\left\{\text { Where, } V_{\text {rms }}=\sqrt{\frac{3 R T}{K N_A T}}\right\}\)

⇒ \(\rho =\frac{P M_0}{R T}=\frac{P M N A}{K N_A T}\)

∴ \(\rho =\frac{P m}{K T}\)

Read and Learn More NEET Physics MCQs

Question 3. In the given (V-T) diagram, what is the relation between pressure p₁ and p₂.

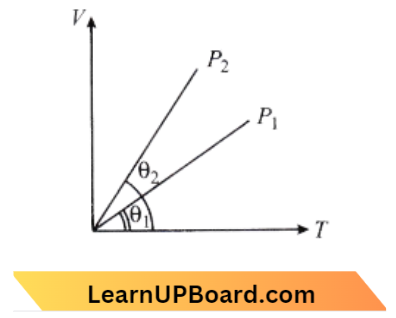
1. P2 = P₁
2. P₂>P₁
3. P₂<P₁
4. Cannot be predicted

Answer: 3. P2<P1

As we know,

PV = nRT

⇒ \(\frac{\mathrm{V}}{\mathrm{T}}=\frac{\mathrm{nR}}{\mathrm{P}}\)

The slope of the graph \(\propto \frac{1}{P}\).

Question 4. At 10°C the value of the density of a fixed mass of an ideal gas divided by its pressure is x. At 110°C this ratio is:

1. x
2. \(\frac{383}{283} x\)
3. \(\frac{10}{110} x\)
4. \(\frac{283}{383} x\)

Answer: 4. \(\frac{283}{383} x\)

Using equation,

PV = nRT

or \(\frac{P V}{M}=\frac{1}{M_0} R T\)

or \(\frac{P}{\rho} =\frac{R T}{M_0} \)

r = \(\frac{\rho}{P}=\frac{M}{R T}\)

∴ \(\frac{\rho}{P} \propto \frac{1}{T}\)

So, \(\frac{r_2}{r_1}=\frac{T_1}{T_2}=\frac{273+10}{273+110}=\frac{283}{383}\)

or \(r_2=\frac{283}{383} r_1\)

Question 5. The equation of state for 5 g of oxygen at a pressure P and temperature T, when occupying a volume V, will be (where R is the gas constant):

1. PV= (5/32)RT
2. PV= 5RT
3. PV= (5/2)RT
4. PV= (5/16)RT

Answer: 1. PV= (5/32)RT

We know that, PV = nRT

n=\(\frac{m}{\text { molecular mass }}=\frac{5}{32}\)

P V=\(\left(\frac{5}{32}\right) R T \)

Question 6. Three containers of the same volume contain three different gases. The masses of the molecules are m₁, m_2, and m₃ and the number of molecules in their respective containers are N₁, N_2, and N₃. The gas pressure in the containers is p₁, p_2, and p₃ respectively. All the gases are now mixed and put in one of these containers. The pressure p of the mixture will be:

1. \(p<\left(p_1+p_2+p_3\right)\)
2. p=\(\frac{p_1+p_2+p_3}{3}\)
3. p=\(p_1+p_2+p_3\)
4. \(p>\left(p_1+p_2+p_3\right)\)

Answer: 1. \(p<\left(p_1+p_2+p_3\right)\)

According to Dalton’s law of partial pressure, the total pressure exerted by a mixture of gases that do not interact with each other is equal to the sum of the partial pressures that each would impose if alone occupied the same volume at the given temperature. When various gases are combined in one container, the mixture’s pressure P will be P=P₁+P₂+P₃

Question 7. A ideal gas equation can be written as:\(P=\frac{\rho R T}{M_0}\) where, ρ and M₀ are respectively :

1. mass density, the mass of the gas
2. number density, molar mass
3. mass density, molar mass
4. number density, the mass of the gas

Answer: 3. mass density, molar mass

The ideal gas equation is given by:

P V = nRT

P V =\(\frac{m}{\mathrm{M}} R T\)

P =\(\frac{m}{V}\left(\frac{R T}{M_0}\right)\)

P =\(\rho\left(\frac{R T}{M_0}\right)\)

∴ \(\mathrm{P} =\frac{m}{\mathrm{~V}}\)

Where, \(\rho \text { and } \mathrm{M}_{\mathrm{o}}\) are mass density and molar mass respectively.

Question 8. The average thermal energy for a monoatomic gas is (where Kg is Boltzmann constant and T is the absolute temperature.):

1. \(\frac{3}{2} K_B T\)
2. \(\frac{5}{2} K_B T\)
3. \(\frac{7}{2} K_B T\)
4. \(\frac{1}{2} K_B T\)

Answer: 1. \(\frac{3}{2} K_B T\)

The average thermal energy of the system with a degree of freedom is equal to its average energy.

Average thermal energy =\(\frac{f}{2} K_B \cdot T\)

For monoatomic gas f=3

Average thermal energy =\(\frac{3}{2} K_B \cdot T\)

Where, \(K_B\)= Boltzmann constant

and T = absolute temperature.

Question 9. An increase in the temperature of a gas-filled container would lead to:

1. increase in its kinetic energy
2. decrease in its pressure
3. decrease in intermolecular distance
4. increase in its mass.

Answer: 1. increase in its kinetic energy

An increase in the temperature of a gas-filled container leads to an increase in its kinetic energy.

Question 10. At what temperature will the RMS speed of oxygen molecules become just sufficient for escaping from the Earth’s atmosphere? Given : mass of oxygen molecule m= 2.76 x 10^-26 kg; Boltzmann’s constant kB= 1.38 x 10^-23Jk

1. 5.016 x 10⁴ K
2. 8.326 x 10⁴ K
3. 2.508 x 10⁴ K
4. 1.254 x 10⁴ K

Answer: 2. 8.326 x 10⁴ K

Escape velocity is the minimum velocity with which when a body is projected, so as to enable it to just overcome the gravitational pull of that surface i.e.Earth

Given: \(k_B =1.38 \times 10^{-23} \mathrm{Jk}^{-1}\)

⇒ \(m_0 =2.76 \times 10^{-26} \mathrm{~g}\)

Escape Velocity, \(v_e=\sqrt{\frac{2 G M}{R}}=\sqrt{2 g R}\)

⇒ \(v_e =\sqrt{2 \times 9.8 \times 6.4 \times 10^6}\)

=\(11.2 \mathrm{kms}^{-1}=11200 \mathrm{~ms}^{-1}\)

⇒ [Since radius of earth R=6.4 \(\times 10^6 \mathrm{~m}]\)

Say at temperature T it attains escape velocity

⇒ \(v_e =\sqrt{\frac{3 K_B T}{m_{02}}}\)

11200 =\(\sqrt{\frac{3 K_B T}{m_{02}}}\)

T =\(\frac{\left(11.2 \times 10^3\right)^2 \times 2.76 \times 10^{-26}}{3 \times 1.38 \times 10^{-23}}\)

∴ T =8.326 \(\times 10^4 \mathrm{k}\)

Question 11. The molecules of a given mass of a gas have r.m.s. velocity of 200 ms^-1 at 27°C and 1.0 x 10s Nm^-2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 x 105 Nm^-2, the RMS velocity of its molecules in ms^-1 is:

1. \(\frac{400}{\sqrt{3}}\)
2. \(\frac{100 \sqrt{2}}{3}\)
3. \(\frac{100}{3}\)
4. \(100 \sqrt{2}\)

Answer: 1. \(\frac{400}{\sqrt{3}}\)

Given, \(v_{\mathrm{rms}}=200 \mathrm{~ms}^{-1}, T_1=300 \mathrm{~K}, P_1=10_5 \mathrm{~N} / \mathrm{m}^2\)

⇒ \(T_2=400 \mathrm{~K}, P_2=0.05 \times 10^5 \mathrm{~N} / \mathrm{m}\)

We know that, \(v_{\text {rms }}=\sqrt{\frac{3 k_B T}{m}}\)

⇒ \(v_{\text {rms }} \propto \sqrt{T}\)

⇒  \(\frac{v_{27}}{v_{127}}=\sqrt{\frac{27+273}{127+273}}=\sqrt{\frac{300}{400}}=\frac{\sqrt{3}}{2}\)

∴ \(v_{\mathrm{rms}}=\frac{200 \times 2}{\sqrt{3}} \mathrm{~m} / \mathrm{s}=\frac{400}{\sqrt{3}} \mathrm{~m} / \mathrm{s}\)

Question 12. In a vessel, the gas is at pressure P, if the mass of all the molecules is halved of their speed is double, then the resultant pressure will be :

1. 2P
2. P
3. P/2
4. 4P

Answer: 1. 2P

The equation of pressure is, \(P=\frac{1}{3} \frac{m \mathrm{~N}}{V} v_{r m s}^2\)  Equation 1

where, m = mass of each molecule

N = number of molecules

Z = volume of the gas

According to the question: Mass of all molecules is halved and velocity is double then

⇒ \(P^{\prime} =\frac{1}{3}\left(\frac{m}{2}\right) \times \frac{N}{V} \times\left(2 v_{r m s}\right)^2 \)

=\(\frac{2}{3} \frac{m N}{V} v_{r m s}^2 \)

=\(2 \times \frac{1}{3} \frac{m \mathrm{~N}}{V} v_{r m s}^2\)

=2 P

compare with eq (1), P’ = 2P

Question 13. The pressure of a gas is raised from 27°C to 927°C. The root mean square speed:

1. Is\(\sqrt{\left(\frac{927}{27}\right)}\)times the earlier value
2. remains the same
3. gets halved
4. gets doubled

Answer: 3. gets halved

The square root of the mean of the squares of the random velocities of individual molecules in a gas is defined as RMS speed.

RMS speed is calculated by using the Maxwell distribution law \(C_{\mathrm{rms}}=\sqrt{\left(\frac{3 k T}{m}\right)}\)

⇒  \(C_{\mathrm{rms}} \propto \sqrt{T}\)

For two different cases i.e. at two different temperatures,

⇒  \(\frac{\left(C_{\text {rms }}\right)_1}{\left(C_{\text {rms }}\right)_2}=\sqrt{\frac{T_1}{T_2}}\)

Here, \(T_1=27^{\circ} \mathrm{C}=300 \mathrm{~K}\)

⇒  \(T_2=927^{\circ} \mathrm{C}=1200 \mathrm{~K}\)

⇒  \(\frac{\left(C_{\mathrm{rms}}\right)_1}{\left(C_{\mathrm{rms}}\right)_2}=\sqrt{\frac{300}{1200}}=\frac{1}{2}\)

⇒  \(\left(C_{\mathrm{rms}}\right)_2=2\left(C_{\mathrm{rms}}\right)_1\)

∴ Hence, the RMS speed will be doubled.

Question 14. The relation between pressure (p) and energy (E) of a gas is:

1. p=\(\frac{2}{3} E\)
2. p=\(\frac{1}{3} E\)
3. p=\(\frac{3}{2} E\)
4. p=3 E

Answer: 1. p=\(\frac{2}{3} E\)

We have, pressure exerted by gas molecules,

p=\(\frac{1}{3} \rho_{\mathrm{v}}^{-}\)  →  Equation 1

where, \(\rho\)= density of gas

⇒ \(\bar{v}\)= average velocity of gas molecules, or  \(p=\frac{2}{3} n \cdot \frac{1}{2} m_{\mathrm{v}} ( since \rho=mn)\)

Here, \(\frac{1}{2} m \overline{\mathrm{v}}\)= average kinetic energy of a gas molecule \((\overline{\mathrm{KE}})\)

Therefore,p=\(\frac{2}{3} n \overline{\mathrm{KE}}\)

If the total number of gas molecules in volume V is N then, Therefore, No. of gas molecules per unit volume

n = \(\frac{N}{V} \)

P = \(\frac{2}{3} \cdot \frac{N}{V}\left(\frac{1}{2} m v^2\right)\)

{or} P V = \(\frac{2}{3} N(\overline{\mathrm{KE}}) \quad\left[K E=\frac{1}{2} m v^2\right]\)

Also, from Eq. (1),

P V=\(\frac{2}{3} \cdot \frac{1}{2} \rho v^2\)

Here, \(\frac{1}{2} \rho v^{-2}\)= average kinetic energy of the gas per unit volume.

Therefore, P=\(\frac{2}{3} E\)

Question 15. According to the kinetic theory of gases, at absolute zero temperature:

1. water freezes
2. liquid helium freezes
3. molecular motion stops
4. liquid hydrogen freezes

Answer: 4. liquid hydrogen freezes

According to the kinetic theory of gases, the pressure P exerted by one mole of an ideal gas,

P = \(\frac{1}{3} \frac{M}{V} c^2\)

or \(\frac{1}{3} M c^2\)

or \(\frac{1}{3} M c^2=\mathrm{RT}\)  → Equation 1

where c is the root mean square velocity of gas. From (1), when T = 0, c = 0

Hence, the absolute zero temperature can be defined as the temperature at which the root mean square velocity of the gas molecules falls to zero. At absolute zero temperature, the molecular motion comes to a stop.

Question 16. Match Column – 1 and Column – 2 and choose the correct match from the given choices:

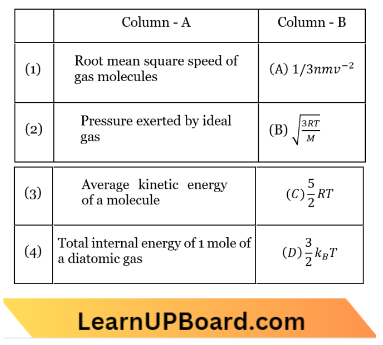
1. 1 – C,  2  – A,   3 – D,  4 -B
2. 1 – B,  2  –  C    3 – D, 4 – A
3. 1 – B,  2 – A,   3 – D, 4 – C
4. 1 – C,  2 – B,   3 – A,  4 – D

Answer: 3. 1 – B,  2 – A,   3 – D, 4 – C

The RMS velocity is, \(v_{r m s}=\sqrt{\frac{3 R T}{M}}\)

The pressure exerted by an ideal gas is \(\frac{1}{3} m n v^{-2}\).

Average kinetic energy of a molecule \(\frac{3}{2} k_B T\).

The total internal energy of 1 mole of a diatomic gas, U=\(\frac{5}{2} R T\).

Question 17. The volume ( V) of a monoatomic gas varies with its temperature (7), as shown in the graph. The ratio of work done by the gas, to the heat absorbed by it, when it undergoes a change from state A to B is:

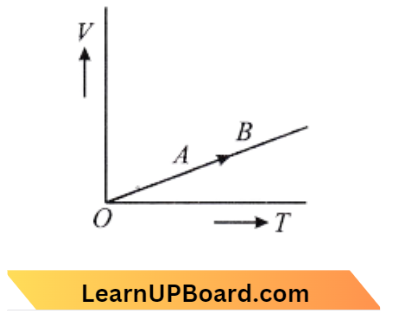
1. \(\frac{1}{3}\)
2. \(\frac{2}{3}\)
3. \(\frac{2}{5}\)
4. \(\frac{2}{7}\)

Answer: 3. \(\frac{2}{5}\)

The given graph shows that Volume V \(\propto\) temperature

⇒ \(\frac{V}{T}\)= Constant

This is an isobaric process,

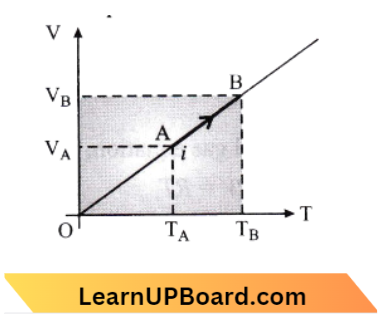
We know that Work done, \(\Delta W=P \Delta V=n R \Delta T\)  →  Equation 1

Absorbed heat, \(\Delta Q=n C_P D T=n C_p\left(T_B-T_A\right)\)  → Equation 2

For monoatomic gas, f=3

⇒ \(C_P=\left(R+\frac{3}{2} R\right)=\frac{5}{2} R\)

Then eq.(2) becomes,

⇒ \(\Delta \mathrm{Q}=n\left(\frac{5}{2} R\right)\left(T_B-T_A\right)\)  Equation 2

Divided eq. (1) by (2) we write,

⇒ \(\frac{\Delta \mathrm{W}}{\Delta \mathrm{Q}}=\frac{n R[T_B-T_A]}{n(\frac{5}{2}}\)

∴ \(R\left[T_B-T_A\right]=\frac{2}{5}\)

Question 18. A gas mixture consists of 2 moles of O₂ and 4 moles of Ar at temperature T. Neglecting all vibrational modes, the total internal energy of the system is:

1. ART
2. 15RT
3. 9RT
4. 11 RT

Answer: 4. 11 RT

Total internal energy of system = Internal energy of oxygen molecules + internal energy of argon molecules

= \(\frac{f_1}{2} \eta_1 R T+\frac{f_2}{2} \eta_2 R T\)

= \(\frac{5}{2} \times 2 R T+\frac{3}{2} \times 4 R T=11 R T\)

Question 19. A mass of diatomic gas (y = 1.4) at a pressure of 2 atm is compressed adiabatically so that its temperature rises from 27° C to 927° C. The pressure of the gas at the final state is:

1. 28 atm
2. 68.7 atm
3. 256 atm
4. 8 atm

Answer: 3. 256 atm

⇒ \(T_1=273+27=300 \mathrm{~K}\)

⇒ \(T_2=273+927=1200 \mathrm{~K}\)

for adiabatic process, \(P V^\gamma\) = constant

⇒ \(P\left(\frac{T}{P}\right)^\gamma\) = constant {because P V=n R T}

⇒ \(\frac{P_2}{P_1} =\left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\gamma-1}}\)

⇒ \(P_2 =P_1\left(\frac{T_2}{T_1}\right)^{\frac{\gamma}{\gamma-1}}\)

= \(2\left(\frac{1200}{300}\right)^{\frac{1.4}{1.4-1}}\)

= \((2)(4)^{\frac{1.4}{1.4-1}}\)

= 256 atm

Question 20. The gas carbon-monoxide (CO) and nitrogen (N₂) at the same temperature have kinetic energies E₁ and E₂ respectively. Then:

1. E₁ = E₂
2. E₁ > E₂
3. E₁ < E₂
4. E₁ and E₂ cannot be compared.

Answer: 1. E₁ = E₂

Since carbon monoxide (CO) and nitrogen (N₂) are diatomic gases. So, their kinetic energies will be equal, i.e. E₁ = E₂.

Question 21. An ideal gas at 27°C is compressed adiabatically to \(\frac{8}{27}\)of its original volume. The rise in temperature is [Given: \(\gamma=\frac{5}{3}\)

1. 475° C
2. 402° C
3. 275° C
4. 375° C

Answer: 4. 375° C

In an adiabatic process, \(P V^\gamma\)= constant  → Equation 1

Where, P= pressure, V= volume and \(\gamma\)= atomicity of gas,

Now from the ideal gas equation, P V=R T  (for one mole)

or P=\(\frac{R T}{V}\) (where, R= gas constant) →  Equation  2

From Eqs. (1) and (2), we get,

⇒ \(\left(\frac{R T}{V}\right) V^\gamma\) = constant

⇒ \(T V^{\gamma-1}\) = constant

For two different cases of temperature and volume of a gas,

⇒ \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)

or \(\frac{T_2}{T_1}=\left(\frac{V_1}{V_2}\right)^{\gamma-1}\)  →   Equation  3

Given, \(T_1 =27^{\circ} \mathrm{C}\)

= 27+273=300 \(\mathrm{~K}\)

And \(\frac{V_2}{V_1}=\frac{8}{27}\), \(\gamma=\frac{5}{3}\)

Substituting these values in Eq. (3), we get,

⇒ \(\frac{T_2}{300}=\left(\frac{27}{8}\right)^{5 / 3-1}\)

or \(\frac{T_2}{300}=\left[\left(\frac{3}{2}\right)^3\right]^{2 / 3}\)

or \(\frac{T_2}{300}=\left(\frac{3}{2}\right)^2=\frac{9}{4}\)

⇒ \(T_2=\frac{9}{4} \times 300=675 \mathrm{~K}=402^{\circ} \mathrm{C}\)

Thus, rise in temperature, = \(T_2-T_1\)

= \(402^{\circ} \mathrm{C}-27^{\circ} \mathrm{C}=375^{\circ} \mathrm{C}\)

Question 22. The degrees of freedom of a molecule of a triatomic gas are:

1. 2
2. 4
3. 6
4. 8

Answer: 3. 6

• A triatomic gas molecule tends to rotate along one of three coordinate axes. As a result, it possesses six degrees of freedom, 3 of which are translational and 3 of which are rotational.
• A triatomic molecule with a high enough temperature has 2 vibrational degrees of freedom. But, as there is no temperature requirement given. So, by simply assuming a triatomic gas molecule at room temperature has 6 degrees of freedom.
• Thus,(3 translational degrees + 3 rotational degrees) at room temperature.

Question 23. A diatomic gas initially at 18°C is compressed adiabatically to one-eight of its original volume. The temperature after compression will be:

1. 18° C
2. 668.4° K
3. 395.4° C
4. 144° C

Answer: 2. 668.4° K

⇒ \(T V^{\gamma-1}\)= constant

For two different cases, of temperature and volume of the gas.

⇒ \(T_1 V_1^{\gamma-1}=T_2 V_2^{\gamma-1}\)  →  Equation 1

Given, the initial temperature,

⇒ \(T_1=18^{\circ} \mathrm{C}=291 \mathrm{~K}\)

Let initial volume, \(V_1\)=V then the final volume, \(V_2=\left(\frac{1}{8}\right)\) V Given,

Putting these values in Eq. (1),

⇒ \(T_2 =291\left(\frac{V_1}{V_2}\right)^{\gamma-1}=291\left(\frac{V}{\left(\frac{1}{8}\right) V}\right)^{7 / 5-1}\)

= 668.4 \(\mathrm{~K}\)

Question 24. The number of translational degrees of freedom for a diatomic gas is:

1. 2
2. 3
3. 5
4. 6

Answer: 2. 3

Several degrees of freedom of a dynamical system is calculated by subtracting the number of independent relations from the total number of coordinates required to describe the positions of the system’s constituent particles.

If I is the number of particles in the system, R is the number of independent relations between the particles, and N is the system’s degree of freedom, then, N =3A – R

Every monoatomic, diatomic, and triatomic gas has three translational degrees of freedom

Question 25. The value of \(\left(\gamma=\frac{C_P}{C_V}\right)\)for hydrogen, helium and another
ideal diatomic gas X (whose molecules are not rigid but have an additional vibration mode), are respectively equal to :

1. \(\frac{7}{5}, \frac{5}{3}, \frac{9}{7}\)
2. \(\frac{5}{3}, \frac{7}{5}, \frac{9}{7}\)
3. \(\frac{5}{3}, \frac{7}{5}, \frac{7}{5}\)
4. \(\frac{7}{5}, \frac{5}{3}, \frac{7}{5}\)

Answer: 1. \(\frac{7}{5}, \frac{5}{3}, \frac{9}{7}\)

⇒ \(\gamma=\frac{C_P}{C_V}\)

where \(C_P\)= molar heat capacity constant pressure and \(C_V\)= molar heat capacity at constant volume Also, \(C_P=C_V+R\) (from Mayer’s relation)

⇒ \(C_V=\frac{f}{2} R\) (where, f= degree of freedom)

⇒ \(C_P=\left(\frac{f}{2}+1\right) R\)

So eq. (1) becomes,

⇒ \(\gamma=1+\frac{2}{f}\)

For hydrogen gas, which is diatomic, the degree of freedom is 5 (3 translational, 2 rotational).

⇒ \(\gamma=1+\frac{2}{5}=\frac{7}{5}\)

For helium gas, which is monatomic, the degree of freedom is 3 ( 3 translational only).

⇒ \(\gamma=1+\frac{2}{3}=\frac{5}{3}\)

The diatomic gas X also has vibrational motion, so the degree of freedom is 7 (3 translational, 2 rotational, and 2 vibrational)

∴ \(\gamma=1+\frac{2}{7}=\frac{9}{7}\)

Question 26. One mole of an ideal monatomic gas undergoes a process described by the equation pV₃ =constant. The heat capacity of the gas during this process is:

1. \(\frac{3}{2} R\)
2. \(\frac{5}{2} R\)
3. 2R
4. R

Answer: 4. R

From the polytropic process,

⇒ \(P V^x\)= constant

Heat capacity in the polytropic process is given by,

C=\(C_y+\frac{R}{1-x}\)

From question, \(\mathrm{PV}^3\) = constant

x = 3  →  Equation 1

and also gas is monoatomic,

So,\(C_V=\frac{3}{2} R \)  →  Equation 2

from above formula, C =\(\left[\frac{3}{2} R+\frac{R}{1-3}\right]\)

=\(\frac{3}{2} R-\frac{R}{3}\)=R

Question 27. The ratio of the specific heat \(\frac{C_P}{C_V}=\gamma\) in terms of degrees of freedom (n) is given by:

1. \(\left(1+\frac{1}{n}\right)\)
2. \(\left(1+\frac{n}{3}\right)\)
3. \(\left(1+\frac{2}{n}\right)\)
4. \(\left(1+\frac{n}{2}\right)\)

Answer: 3. \(\left(1+\frac{2}{n}\right)\)

We know that specific heat at constant volume is given by,\(C_V=\frac{n}{2} R\)

Where, n = degree of freedom

R = gas constant

And \(C_P-C_V\)=R  [Mayer’s formula]

⇒\(C_P=\frac{n}{2} R+R=R\left(1+\frac{n}{2}\right)\)

⇒ \(\gamma=\frac{C_P}{C_V}=\frac{R\left(1+\frac{n}{2}\right)}{\frac{n}{2} R}\)

= \(\frac{2}{n}+1 \)

Question 28. The molar-specific heats of an ideal gas at constant pressure and volume and denoted by Cp and Cv respectively.  If \(\gamma=\frac{C_P}{C_V}\) and R is the universal gas constant then Cv is equal to:

1. \(\frac{1+\gamma}{1-\gamma}\)
2. \(\frac{R}{(\gamma-1)}\)
3. \(\frac{(\gamma-1)}{R}\)
4. \(\gamma^R\)

Answer: 2. \(\frac{R}{(\gamma-1)}\)

As we know, \(C_P-C_V\) = R and \(\gamma=\frac{C_P}{C_V}\)

⇒ \(C_V =\frac{\mathrm{R}}{\gamma-1}\)

Question 29. The amount of heat energy required to raise the temperature of 1 g of helium at NTP, from T₁K to T₂K is:

1. \(\frac{3}{8} N_a k_B\left(T_2-T_1\right)\)
2. \(\frac{3}{2} N_a k_B\left(T_2-T_1\right)\)
3. \(\frac{3}{4} N_a k_B\left(T_2-T_1\right)\)
4. \(\frac{3}{4} N_a k_B\left(\frac{T_2}{T_1}\right)\)

Answer: 1. \(\frac{3}{8} N_a k_B\left(T_2-T_1\right)\)

Number of moles of 1 \(\mathrm{~g} \mathrm{He}=\frac{1}{4}\)

The amount of heat energy required to raise the temperature of the gas is,

⇒ \(\Delta \mathrm{Q}=n \mathrm{C}_{\mathrm{V}} \Delta \mathrm{T}\)

Here, n=\(\frac{1}{4}, C_V =\frac{3}{2} R\)

= \(\left(\frac{1}{4}\right)\left(\frac{3}{2} R\right)\left(T_2-T_1\right)\)

= \(\frac{3}{8} k_B N_A\left(T_2-T_1\right) . (k_3=\frac{R}{N a})\)

Question 30. The molar specific heat at constant pressure of an ideal gas is (7/2) R. The ratio of specific heat at constant pressure to that at constant volume is:

1. 9/7
2. 7/5
3. 8/7
4. 5/7

Answer: 2. 7/5

Molar-specific heat at constant pressure,

⇒ \(C_P=\frac{7}{2} R\)

We know that, \(C_P-C_V=R\)

⇒ \(C_V =C_P-R \)

= \(\frac{7}{2} R-R=\frac{5}{2} R\)

from (1) and (2),

∴ \(\frac{C_P}{C_V}=\frac{7}{5}\)

Question 31. One mole of an ideal gas at an initial temperature of TK does 6R joules of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is 5/3, the final temperature of the gas will be:

1. (T+2X)K
2. {T-2A)K
3. (T+4)K
4. (T-4)K

Answer: 1. (T+2X)K

We know that work done in the adiabatic process is:

W=\(\frac{-1}{V-1}\left(P_f V_f-P_i V_i\right)\)

⇒ \(6 R=\frac{-1}{\frac{5}{3}-1} R\left(T_f-T_i\right)\)  {Since,P V=n R T}

⇒ \(T_f-T_i=-4\)

∴ \(T_f=(T-4) \mathrm{K}\)

Question 32. If for a gas, \(\frac{R}{C_{\mathrm{v}}}\)= 0.67, this gas is made up of molecules which are:

1. diatomic
2. mixture of diatomic and polyatomic molecules
3. monoatomic
4. polyatomic

Answer: 3. monoatomic

Since, \(C_{\mathrm{v}}=\frac{R}{0.67} \approx 1.5 R=\frac{3}{2} R\)

Hence, it is the case of monoatomic gases

Question 33. For hydrogen gas Cp – Cv = a and oxygen gas C_p – C_v = b, the relation between a and b is given by:

1. a= 16b
2. 16b = a
3. a = 4b
4. a = b

Answer: 4. a = b

Since hydrogen and oxygen are diatomic gases and C_p – C_v = R is the same for all gases. Hence, a: b, assuming C_p and C_v are gram molar specific heats.

Question 34. For a certain gas, the ratio of specific heat is given to be y = 1.5, for this gas:

1. \(C_v=\frac{3 R}{J}\)
2. \(C_p=\frac{3 R}{J}\)
3. \(C_p=\frac{5 R}{J}\)
4. \(C_p=\frac{5 R}{J}\)

Answer: 2. \(C_p=\frac{3 R}{J}\)

We have,\(\gamma=\frac{C_P}{C_V}\)

Given,\(\gamma=1.5=\frac{3}{2}\)

⇒ \(C_V=\frac{2}{3} C_P\)

From Mayer’s formula, \(C_P-C_V =\frac{R}{J}\)

⇒ \(C_P-\frac{2}{3} C_P =\frac{R}{J}\)

⇒ \(\frac{C_P}{3} =\frac{R}{J}\)

∴ \(C_P =\frac{3 R}{J}\)

Question 35. At 27°C a gas is compressed suddenly such that its pressure becomes \(\left(\frac{1}{8}\right)\)of original pressure. Final temperature will be \(\left(\gamma=\frac{5}{3}\right)\)

1. 420 K
2. 300 K
3. -142° C
4. 327 K

Answer: 3. -142° C

In an adiabatic process, PVϒ = k(a constant)  →  Equation 1

where, P = pressure and V = volume and ϒ =atomicity of gas

Again from standard gas equation,\(P V^\gamma =n R T\)

V =\(\frac{R T}{P}\)

Putting the value of V in Eq. (1), we get

⇒ P \(\frac{R^\gamma T^\gamma}{p^\gamma}\)=k or

⇒ \(P^{1-\gamma} T^\gamma=\frac{k}{R^\gamma}\)= another constant or

⇒ \(P^{1-\gamma} T^\gamma\)= constant

For two different cases,

⇒ \(P_1{ }^{1-\gamma} T_1{ }^\gamma=P_2{ }^{1-\gamma} T_2{ }^\gamma\)

⇒ \(\left(\frac{T_2}{T_1}\right)^\gamma =\left(\frac{P_1}{P_2}\right)^{1-\gamma}\)

Here, \(P_2 =\left(\frac{1}{8}\right) P_I\)

⇒ \(T_1 =27^{\circ} \mathrm{C}=273+27=300 \mathrm{~K}\)

⇒ \(T_2 =?, \gamma=\frac{5}{3}\)

⇒ \(\left(\frac{T_2}{300}\right)^{5 / 3} =(8)^{1-5 / 3}=(8)^{-2 / 3}\)

⇒ \(T_2 =130.6 \mathrm{~K}\)

∴\(T_2 =-142^{\circ} \mathrm{C}\)

Question 36. The mean free path X for a gas, with molecular diameter d and number density n, can be expressed as:

1. \(\frac{1}{\sqrt{2} n \pi d^2}\)
2. \(\frac{1}{\sqrt{2} n^2 \pi d^2}\)
3. \(\frac{1}{\sqrt{2} n^2 \pi^2 d^2}\)
4. \(\frac{1}{\sqrt{2} n \pi d}\)

Answer: 1. \(\frac{1}{\sqrt{2} n \pi d^2}\)

The mean free path \(\lambda\) for gas, with molecular diameter d and number density n can be expressed on \(\frac{1}{\sqrt{2} n \pi d^2}\)

Question 37. The mean free path of a molecule of a gas (radius r) is inversely proportional to the:

1. \(r^3\)
2. \(r^2\)
3. r
4. \(\sqrt{r}\)

Answer: 2. \(r^2\)

Mean free path, \(\lambda=\frac{1}{\pi n r^2}\)

∴ \(\lambda \propto \frac{1}{r^2}\)

Question 38. At constant volume, temperature is increased, then:

1. collision on walls will be less.
2. the number of collisions per unit of time will increase.
3. collisions will be in straight lines.
4. collisions will not change.

Answer: 2. the number of collisions per unit of time will increase.

The average velocity of the gas molecules increases as the temperature rises. As a result, more molecules collide with the walls. Hence, the number of collisions per unit time will increase.

Question 39. A polyatomic gas with n degrees of freedom has a mean energy per molecule given by:

1. \(\frac{n k T}{N}\)
2. \(\frac{n k T}{2 N}\)
3. \(\frac{n k T}{2}\)
4. \(\frac{3 k T}{2}\)

Answer: 3. \(\frac{n k T}{2}\)

According to the law of energy equipartition, for any dynamical system in thermal equilibrium, the total energy is distributed equally across all degrees of freedom, and the energy associated with each molecule per degree of freedom equals 12kT. The mean energy per molecule for a polyatomic gas with n degrees of freedom is \(\frac{1}{2} n k T\).

Where,k = Boltzmann

constant n = degree of freedom,

and T- Temperature