Rigid Body Dynamics MCQs
NEET Physics For System Of Particles And Rotational Motion Multiple Choice Questions
Question 1. Three identical spheres, each of mass M, are placed at the comers of a right-angled triangle with mutually perpendicular sides equal to 2 m (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin, the position vector of the centre of mass is
- \(2(\hat{i}+\hat{j})\)
- \((\hat{i}+\hat{j})\)
- \(\frac{2}{3}(\hat{i}+\hat{j})\)
- \(\frac{4}{3}(\hat{i}+\hat{j})\)
Answer: 2. \((\hat{i}+\hat{j})\)
See The Figure,
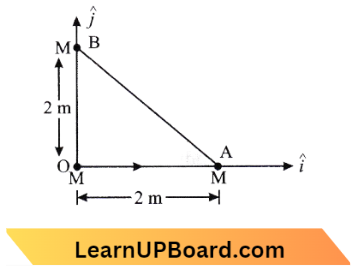
Given
Three identical spheres, each of mass M, are placed at the comers of a right-angled triangle with mutually perpendicular sides equal to 2 m (see figure). Taking the point of intersection of the two mutually perpendicular sides as the origin,
⇒ \(\mathrm{OA}=2 \hat{i}\)
⇒ \(\mathrm{OB}=2 \hat{j}\)
Position vector of centre of mass, \(\mathrm{R}_{\mathrm{CM}} =\frac{m_1 r_1+m_2 r_2}{m_1+m_2}\)
=\(\frac{M \cdot \mathrm{OA}+M \cdot \mathrm{OB}}{M+M}\)
=\(\frac{M \times 2 \hat{i}+M \times 2 \hat{j}}{2 M}=\hat{i}+\hat{j}\)
Question 2. Two particles of mass 5 kg and 10 kg respectively are attached to the two ends of a rigid rod of length 1 m with negligible mass. The centre of mass of the system from the 5 kg particle is nearly at a distance of:
- 50 cm
- 67 cm
- 80 cm
- 33 cm
Answer: 2. 67 cm
Given That,
Two particles of mass 5 kg and 10 kg respectively are attached to the two ends of a rigid rod of length 1 m with negligible mass.
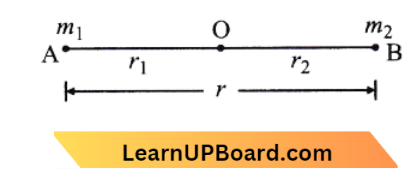
⇒ \(\frac{m_1 r_1-m_2 r_2}{m_1+m_2}\) =0
⇒ \(5 r_1-10 r_2\) =0
⇒ \(r_2 =\frac{r_1}{2}\)
⇒ \(r_1+r_2\) =100
⇒ \(r_1+\frac{r_1}{2}\) =100
⇒ \(3 r_1\) =200
∴ \(r_1 =\frac{200}{3}=67 \mathrm{~cm}\)
Read and Learn More NEET Physics MCQs
Rigid Body Dynamics MCQs
Question 3. Three masses are placed on the x-axis: 300 g at origin, 500 g at x = 40 cm and 400 g at x = 70 cm. The distance of the centre of mass of the origin is:
- 40 cm
- 45 cm
- 50 cm
- 30 cm
Answer: 1. 40 cm
⇒ Centre of mass\(r_{\mathrm{cm}} =\frac{m_1 x_1+m_2 x_2+m_3 x_3}{m_1+m_2+m_3}\)
=\(\frac{300 \times 0+500 \times 40+400 \times 70}{300+500+400}\)
=40 cm
Question 4. Two bodies of mass 1 kg and 3 kg have position vectors \(\hat{i}+2 \hat{j}+\hat{k}\) and \(-3 \hat{i}+2 \hat{j}+\hat{k}\) respectively. The centre of mass of this system has a position vector:
- \(-2 \hat{i}+2 \hat{k}\)
- \(-2 \hat{i}-\hat{j}+\hat{k}\)
- \(2 \hat{i}-\hat{j}-2 \hat{k}\)
- \(-\hat{i}-\hat{j}+\hat{k}\)
Answer: 2. \(-2 \hat{i}-\hat{j}+\hat{k}\)
According to the question,
Position Vector\(\vec{r} =\frac{m_1 \vec{r}_1+m_2 \vec{r}_2}{m_1+m_2}\)
⇒ \(\vec{r} =\frac{1(\hat{i}+2 \hat{j}+k)+3(-3 \hat{i}-2 \hat{j}+\hat{k})}{1+3}\)
⇒ \(\vec{r} =\frac{1}{4}(-8 \hat{i}-2 \hat{j}+4 \hat{k})\)
⇒ \(\vec{r} =-2 \hat{i}-2 \hat{j}+\hat{k}\)
Question 5. A uniform rod of length l and mass m is free to rotate in a vertical plane about A. The rod initially in a horizontal position is released. The initial angular acceleration of the rod is (moment of inertia of the rod about A is \(\frac{m l^2}{3}\):

- \(m g \frac{l}{2}\)
- \(\frac{3 g}{2 l}\)
- \(\frac{2 l}{3 g}\)
- \(\frac{3 g}{2 l^2}\)
Answer: 2. \(\frac{3 g}{2 l}\)
Here torque,
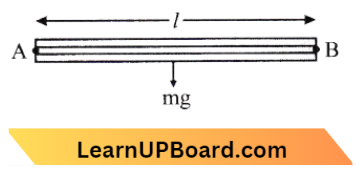
The moment of Inertia of the rod about A is:
I=\(\frac{m l^2}{3}\)
Angular acceleration of the rod is \(\alpha=\frac{\tau}{I}\)
∴ \(\alpha=\frac{m g\left(\frac{1}{2}\right)}{\frac{m l^2}{3}}=\frac{3 g}{2 l}\)
Rigid Body Dynamics MCQs
Question 6. Consider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the mass centre of a particle through a distance d, by what distance would the particle of mass m2 move to keep the mass centre of particles at the original position?
- \(\frac{m_1}{m_1+m_2} d\)
- \(\frac{m_1}{m_2} d\)
- \(\frac{d\left(m_1+m_2\right)}{m_1}\)
- \(\frac{m_2}{m_1}\)
Answer: 2. \(\frac{m_1}{m_2} d\)
We know that, \(\mathrm{CM}=\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
After changing the position of m1 and keeping the position of C.M. the same.
C.M. =\(\frac{m_1\left(x_1 d\right)+m_2\left(\mathrm{x}_2-d_2\right)}{m_1+m_2}\)
0 =\(\frac{m_1 d-m_2 d_2}{m_1+m_2}\)
⇒ \(d_2 =\frac{m_1}{m_2} d\)
∴ C.M. =\(\frac{m_1 x_1+m_2 x_2}{m_1+m_2}\)
Question 7. Consider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of the particles through a distance d, by what distance would be particle of mass m2 move to keep the centre of mass of the particles at the original position?
- \(\frac{m_1}{m_1+m_2} d\)
- \(\frac{m_1}{m_2} d\)
- d
- \(\frac{m_2}{m_1} d\)
Answer: 2. \(\frac{m_1}{m_2} d\)
After changing the position of m1 and keeping the position of C.M. same
C.M.=\(\frac{m_1\left(x_1-d\right)+m_2\left(x_2+d_2\right)}{m_1+m_2}\)
0 =\(\frac{-m_1 d+m_2 d_2}{m_1+m_2}\)
[Substituting value of C.M. from (1)
∴ \(d_2=\frac{m_1}{m_2} d\)
Motion Of Systems Of Particles MCQs
Question 8. Three identical metal balls, each of radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed when the centres of the three balls are joined. The centre of the mass of the system is located at:
- line joining centres of my two balls
- centre of one of the balls
- horizontal surface
- point of intersection of the medians
Answer: 4. point of intersection of the medians
Centre of mass of each ball lies on the centre
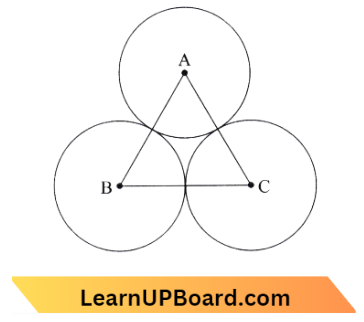
The Centre of mass of the combined body will be at the centroid of an equilateral triangle.
Question 9. Two objects of mass 10 kg and 20 kg respectively are connected to the two ends of a rigid rod of length 10 m with negligible mass. The distance of the centre of mass of the system from the 10 kg mass is :
- \(\frac{20}{3} m\)
- \(10 \mathrm{~m}\)
- \(5 \mathrm{~m}\)
- \(\frac{10}{3} m\)
Answer: 1. \(\frac{20}{3} m\)
Given, M1 = 10kg, M2 = 20kg,
Length of rod = 10 m
Let M1 be at the origin, and then X1 and X2 are 0 and 10 m respectively.
Centre of mass, X=\(\frac{M_1 X_1+M_2 X_2}{M_1+M_2}\)
Putting the values in above equation we get, X=\(\frac{10 \times 0+20 \times 10}{10+20}=\frac{200}{30}=\frac{20}{3}\)
The distance of the centre of mass of the system from the 10 kg mass is: 20/3 m
Motion Of Systems Of Particles MCQs
Question 10. Two persons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat. The length of the boat is 3.0 m and weighs 100 kg. The 55 kg man walks up to the 65 kg man and sits with him. If the boat is in still water. The centre of mass of the system shifts by:
- 3.0 m
- 2.3 m
- zero
- 0.75 m
Answer: 3. zero
Since no external force is applied to the system. And centre of mass (CM) be at rest. So our answer is option (C) zero
Question 11. The resultant of \(\vec{A}\) x 0 will be equal to:
- zero
- A
- zero vector
- unit vector
Answer: 3. zero vector
∴ \(\vec{A} \times 0\) is a zero vector
Question 12. Vectors, \(\vec{A}, \vec{B} \text { and } \vec{C}\) are such that \(\vec{A} \cdot \vec{B}\) = 0 and \(\vec{A} \cdot \vec{C}\)= 0. Then the vector parallel to A is:
- \(\vec{A} \times \vec{B}\)
- \(\vec{B}+\vec{C}\)
- \(\vec{B} \times \vec{C}\)
- \(\vec{B}and \vec{C}\)
Answer: 3. \(\vec{B} \times \vec{C}\)
Vector triple product of three vectors \(\vec{A}, \vec{B}\) and \(\vec{C}\) is:
Given : \(\vec{A} \times(\vec{B} \times \vec{C})=(\vec{A} \cdot \vec{C}) \vec{B}-(\vec{A} \cdot \vec{B}) \vec{C}\)
⇒ \(\vec{A} \cdot \vec{B}=0, \vec{A} \cdot \vec{C}\)=0
⇒ \(\vec{A} \times(\vec{B} \times \vec{C})\)=0
∴ Thus the vector \(\vec{A}\) is parallel to vector \(\vec{B} \times \vec{C}\).
Motion Of Systems Of Particles MCQs
Question 13.\(\vec{A} \text { and } \vec{B}\) are two vectors and θ is the angle between them, if \(|\vec{A} \times \vec{B}|=\sqrt{3}(\vec{A} \cdot \vec{B})\), the value of θ is:
- 45°
- 30°
- 90°
- 60°
Answer: 4. 60°
⇒ \(|\vec{A} \times \vec{B}| \) = \(\sqrt{3}(\vec{A} \cdot \vec{B})\)
⇒ \(A B \sin \theta =\sqrt{3} A B \cos \theta\)
or \(\tan \theta =\sqrt{3}\)
or \(\theta =\tan ^{-1} \sqrt{3}=60^{\circ}\)
Question 14. If the angle between the vectors\(\vec{A} \text { and } \vec{B}\) is θ, the value of the product \((\vec{B} \times \vec{A}) \cdot \vec{A}\) A is equal to:
- \(B A^2 \sin \theta\)
- \(B A^2 \cos \theta\)
- \(B A^2 \sin \theta \cos \theta\)
- zero
Answer: 4. zero
Let, \(|\vec{A} \times \vec{B}|=\vec{C}\)
The cross product of ,\(\vec{B}\) and \(\vec{A}\) is perpendicular to the plane containing \(\vec{A} \)and \(\vec{B}\) i.e. perpendicular to \(\vec{A}\)
Therefore Product Of \((\vec{B} \times \vec{A}) \cdot \vec{A}\)=0
Question 15.If \(|\vec{A} \times \vec{B}|=\sqrt{3} \vec{A} \cdot \vec{B}\) then the value of \(|\vec{A}+\vec{B}|\) is:
- \(\left(A^2+B^2+A B\right)^{1 / 2}\)
- \(\left(A^2+B^2+\frac{A B}{\sqrt{3}}\right)^{1 / 2}\)
- A+B
- \(\left(A^2+B^2+\sqrt{3} A B\right)^{1 / 2}\)
Answer: 1. \(\left(A^2+B^2+A B\right)^{1 / 2}\)
⇒ \(|\vec{A} \times \vec{B}| =\sqrt{3} \vec{A} \cdot \vec{B}\)
⇒ \(|\vec{A} \| \vec{B}| \sin \theta =\sqrt{3}|\vec{A} \| \vec{B}| \cos \theta\)
⇒ \(\tan \theta =\sqrt{3}\)
⇒ \(\theta =60^{\circ}\)
⇒ \(|\vec{A}+\vec{B}| =\sqrt{|\vec{A}|^2+|\vec{B}|^2+2|\vec{A} \| \vec{B}| \cos \theta}\)
=\(\left(A^2+B^2+A B\right)^{1 / 2}\)
Motion Of System Of Particles NEET Questions
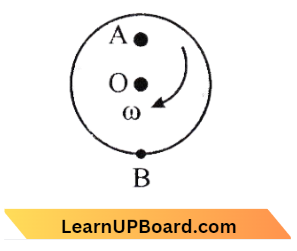
Question 16. A disc is rotating with angular velocity about its axis (without any translation push) on a smooth surface: Find the direction and magnitude of velocity at points B and A
- \( -\omega {R} \) towards left
- \(-\omega {R} \) towards right
- \( +\omega {R} \) towards left
- \( +\omega R \) towards left
Answer: 1. \( -\omega \mathrm{R} towards left \)
In the given question
Velocity at A, \( v_A=\omega\left(\frac{\mathrm{R}}{2}\right)\) towards right
∴ Velocity at B, \(v_B=-\omega\) R towards left
Question 17. What is the value of linear velocity, \(\vec{r}=3 \hat{i}-4 \hat{j}+\hat{k}\) and \(\vec{\omega}=5 \hat{i}-6 \hat{j}+6 \hat{k}\)?
- \(4 \hat{i}-13 \hat{j}+6 \hat{k}\)
- \(18 \hat{i}+13 \hat{j}-2 \hat{k}\)
- \(6 \hat{i}+2 \hat{j}-3 \hat{k}\)
- \(6 \hat{i}-2 \hat{j}+8 \hat{k}\)
Answer: 2. \(18 \hat{i}+13 \hat{j}-2 \hat{k}\)
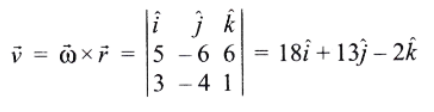
Motion Of System Of Particles NEET Questions
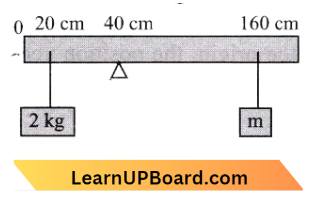
Question 18. A uniform rod of length 200 cm and mass 500 g is balanced on a wedge placed at the 40 cm mark. A mass of 2 kg is suspended from the rod at 20 cm and another unknown mass ‘m’ is suspended from the rod at the 160 cm mark as shown in the figure. Find the value of ‘m’ such that the rod is in equilibrium, (g = 10 m/s²):
- \(\frac{1}{2} \mathrm{~kg}\)
- \(\frac{1}{3} \mathrm{~kg}\)
- \(\frac{1}{6} \mathrm{~kg}\)
- \(\frac{1}{12} \mathrm{~kg}\)
Answer: 4. \(\frac{1}{12} \mathrm{~kg}\)
Applying the principle of momentums, LHM = 2 x 20
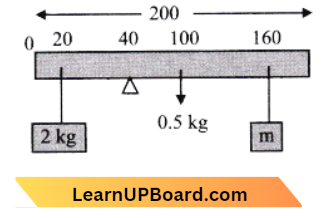
RHM = 0.5 x 60 + m x 120
2 x 20=30+ 120m
10= 120m
∴ \(m=\frac{10}{120}=\frac{1}{12} \mathrm{~kg}\)
Question 19. Find the torque about the origin, when a force of 3\(\hat{\boldsymbol{j}}\)N acts on the particle whose position vector is \(\hat{k}\)
- \(6 \hat{j} \mathrm{~N}-\mathrm{m}\)
- \(-6 \hat{i} \mathrm{~N}-\mathrm{m}\)
- \(-6 \hat{k} \mathrm{~N}-\mathrm{m}\)
- \(6 \hat{i} \mathrm{~N}-\mathrm{m}\)
Answer: 2. \(-6 \hat{i} \mathrm{~N}-\mathrm{m}\)
According to question, Position vector \(\hat{r} =2 \hat{k} m\)
Force, \({\mathrm{F}} =3 \hat{j} \mathrm{~N}\)
Torque, \(\vec{\tau} =\vec{r} \times \overrightarrow{\mathrm{F}}=2 \hat{k} \times 3 \hat{j}\)
= \(-6 \hat{i}\)
= \(-6 \hat{i} \mathrm{~N}-\mathrm{m}\)
NEET Physics MCQs
Question 20. A force F = \(\vec{F}=\alpha \hat{i}+3 \hat{j}+6 \hat{k}\) is acting at a point r = \(\vec{r}=2 \hat{i}-6 \hat{j}-12 \hat{k}\). The value of a for which angular momentum about the origin is conserved is:
- – 1
- 2
- zero
- 1
Answer: 1. – 1
From the question, Force, \(\vec{F} =\alpha \hat{i}+3 \hat{j}+6 \hat{k}\)
and Position, \(\vec{r} =2 \hat{i}-6 \hat{j}-12 \hat{k}\)
Using the law of conservation of angular moments \(\tau\) =constant
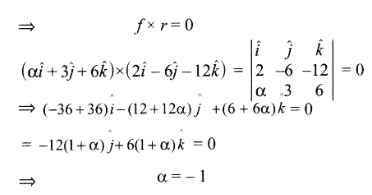
Question 21. When a mass is rotating in a plane about a fixed point, its angular momentum is directed along :
- a line perpendicular to the plane of rotation
- the line at an angle of 45° to the plane of rotation
- the radius
- the tangent to the orbit
Answer: 1. a line perpendicular to the plane of rotation
The formula is L = m (r x v). This shows that when a mass is rotating in a plane about a fixed point, its angular momentum is directed along a line perpendicular to the plane of rotation
Question 22. A magnetic needle suspended parallel to a magnetic field requires \(\sqrt{3} \mathrm{~J}\) J of work to turn it through 60°. The torque needed to maintain the needle in the position will be:
- \(2 \sqrt{3} \mathrm{~J}\)
- \(3 \mathrm{~J}\)
- \(\sqrt{3} \mathrm{~J}\)
- \(\frac{3}{2} \mathrm{~J}\)
Answer: 2. \(3 \mathrm{~J}\)
Work done, W = \(M B \left(\cos \theta_1-\cos \theta_2\right)\)
⇒ \(\sqrt{3} =M B\left(\cos 0^{\circ}-\cos 60^{\circ}\right)\)
⇒ \(\sqrt{3} =\frac{M B}{2}\)
And Torque, \(\tau =M B \sin \theta\)
⇒ \(\tau =M B \sin 60^{\circ}=\sqrt{3} \frac{M B}{2}\)
From Equations 1 And 2
∴ \(\tau=(\sqrt{3})(\sqrt{3})=3 \mathrm{~J}\)
NEET Physics MCQs
Question 23. If \(\vec{F}\) is the force acting on a particle having position vector \(\vec{r} \text { and } \vec{\tau}\) be the torque of this force about the origin, then:
- \(\vec{r} \cdot \vec{\tau} \neq 0\) and \(\vec{F} \cdot \vec{\tau}\)=0
- \(\vec{r} \cdot \vec{\tau}>0\) and \(\vec{F} \cdot \vec{\tau}<0\)
- \(\vec{r} \cdot \vec{\tau}=0\) and \(\vec{F} \cdot \vec{\tau}\)=0
- \(\vec{r} \cdot \vec{\tau}=0\) and \(\vec{F} \cdot \vec{\tau} \neq 0\)
Answer: 3. \(\vec{r} \cdot \vec{\tau}=0\) and \(\vec{F} \cdot \vec{\tau}\)=0
Torque is an axial vector i.e., its direction is always perpendicular to the plane containing vectors \(\vec{r}\) and \(\vec{F}\).
Therefore, \(\vec{\tau}=\vec{r} \times \vec{F}\)
Torque is perpendicular to both \(\vec{r}\) and \(\vec{F}\).
⇒ \(\vec{\tau} \cdot \vec{r}\)=0
∴ \(\vec{F} \cdot \vec{r}\)=0
Question 24. A particle of mass m moves in the XY plane with a velocity v along the straight line AB. If the angular momentum of the particle concerning origin O is LA, when it is at A and LB when it is at B, then:
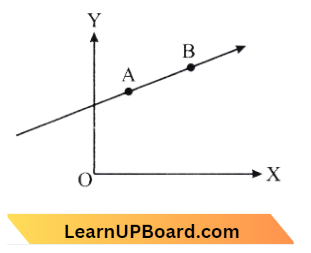
- LA = LB
- the relationship between LA and LB depends upon the slope of the line AB
- LA<LB
- LA>LB
Answer: 1. LA = LB
The moment of Momentum is angular momentum. OP is the same whether the mass is at A or B
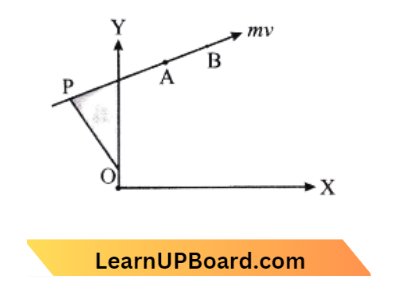
⇒ \(L_A=L_B\)
NEET Physics MCQs
Question 25. Which of the following statements is correct?
1. The centre of mass of a body always coincides with the centre of gravity of the body.
2. The centre of mass of a body is the point at which the total gravitational torque of the body is zero.
3. A couple on a body produces both translation and rotational motion in a body.
4. Mechanical advantage greater than one means that a small effort can be used to lift a large load.
- (2) and (4)
- (1) and (2)
- (2) and (3)
- (3) and (4)
Answer: 1. (2) and (4)
The Centre of mass may or may not coincide with the centre of gravity.
Question 26. A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is:
- \(\frac{w x}{d}\)
- \(\frac{w d}{x}\)
- \(\frac{w(d-x)}{x}\)
- \(\frac{w(d-x)}{d}\)
Answer: 4. \(\frac{w(d-x)}{d}\)
So, W=\(N_1+N_2\) → Equation 1
For equilibrium, \(N_1 x=N_2(d-\boldsymbol{x})\)
From 1 \(N_1 x =\left(W-N_1\right)(d-x)\)
⇒ \(N_1 x =W_d-W_x-N_1 d+N_1 x\)
⇒ \(N_1 d =W(d-x)\)
∴ \(N_1 =\frac{W(d-x)}{d}\)
Class 11 Rigid Body And System Of Particles MCQs
Question 27. ABC is an equilateral triangle with O as its centre. F1, F2 and F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of FT is:
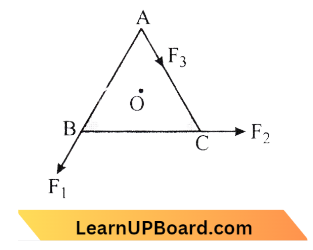
- \(F_1+F_2\)
- \(F_1-F_2\)
- \(\frac{F_1+F_2}{2}\)
- \(2\left(F_1+F_2\right)\)
Answer: 1. \(F_1+F_2\)
Using Torque, \(\tau=F r\)
Clockwise torque, \(\tau =\tau F_1+\tau F_2+\tau F_3\)
0 =\(F_1 r+F_2 r+F_3 r\)
∴ \(F_3 =F_1+F_2\)
Question 28.
- The centre of gravity (CG) of a body is the point at which the weight of the body acts.
- The centre of mass coincides with the centre of gravity if the earth is assumed to have an infinitely large radius.
- To evaluate the gravitational field intensity due to anybody at an external point, the entire mass of the body can be considered to be concentrated at its CG.
- The radius of gyration of anybody rotating about an axis is the length of the perpendicular dropped from the CG of the body to the axis.
Which one of the following pairs of statements is correct?
- (4) and (1)
- (1) and (2)
- (2) and (3)
- (3) and (4)
Answer: 1. (4) and (1)
The CG of a body is the point at which the weight of the body acts.
The radius of gyration of anybody rotating about an axis is the length of the perpendicular dropped from the CG of the body to the axis
Question 29. The ratio of the radius of gyration of a thin uniform disc about an axis passing through its centre and normal to its plane to the radius of gyration of the die about its diameter is ;
- \(\sqrt{2}: 1\)
- 4: 1
- \(1: \sqrt{2}\)
- 2:1
Answer: 1. \(\sqrt{2}: 1\)
The figure of a thin uniform disc and disc is shown below :
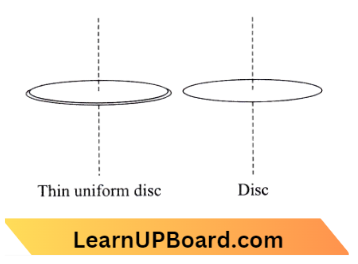
The radius of gyration of a thin uniform disc, k=\(\sqrt{\frac{I}{m}}\) → Equation 1
and moment of inertia of the disc, I=\(\frac{m R^2}{4}\)
Here we have R as the radius, and m as the mass Now, on putting the value in equation (1) we have The radius of gyration of the uniform disc;
⇒ \(k_1=\sqrt{\frac{\frac{m R^2}{2}}{m}}\)
⇒ \(k_1=\sqrt{\frac{R^2}{2}}\) → Equation 2
and the radius of gyration of the uniform disc;
⇒ \(k_2=\sqrt{\frac{m R^2}{4}}\)
⇒ \(k_2=\sqrt{\frac{R^2}{4}}\) → Equation 3
Now, on dividing equation (2) by equation (3) we have;
⇒ \(\frac{k_1}{k_2} =\frac{\sqrt{\frac{R^2}{2}}}{\sqrt{\frac{R^2}{4}}}\)
∴ \(k_1: k_2 =\sqrt{2}: 1\)
Class 11 Rigid Body And System Of Particles MCQs
Question 30. From a circular ring of mass ‘M’ and radius ‘R’, an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of K is:
- \(\frac{3}{4}\)
- \(\frac{7}{8}\)
- \(\frac{1}{4}\)
- \(\frac{1}{8}\)
Answer: 1. \(\frac{3}{4}\)
Given,
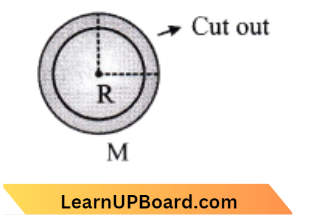
Mass = M
Radius = R
⇒ \(\text { arc } \theta =90^{\circ}\)
⇒ \(\mathrm{I}_{\text {remaining }} =\mathrm{KMR}^2\)
⇒ \(\mathrm{~K}\) =?
⇒ \(\mathrm{I} =r^2 \int d m\)
⇒ \(\frac{d m}{d r} =\frac{\mathrm{M}}{2 \pi \mathrm{R}} d r \)
d m =\(\frac{\mathrm{M}}{2 \pi \mathrm{R}} d r\)
⇒ \(\mathrm{I} =r^2 \int_0^{\frac{3}{2} \pi \mathrm{R}} \frac{M}{2 \pi \mathrm{R}} d r\)
⇒ \(\mathrm{I} =\frac{\mathrm{MR}^2}{2 \pi \mathrm{R}} \cdot \frac{3}{2} \pi \mathrm{R}\)
=\(\frac{3}{4} \mathrm{MR}^2\)
∴ \(\mathrm{~K} =\frac{3}{4}\)
Class 11 Rigid Body And System Of Particles MCQs
Question 31. A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation (Esphere/ECylinder) will be:
- 2 : 3
- 1: 5
- 1: 4
- 3: 1
Answer: 2. 1: 5
Given
A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and radius is also rotating about its geometrical axis with an angular speed twice that of the sphere.
We know That,KE=\(\frac{1}{2} I \omega^2\)
KE of sphere,\(K_S =\frac{1}{2} I_s \omega^2\) Equation 1
= \(\frac{1}{2} \times \frac{2}{5} M R^2 \times \omega^2\)
In KE of cylinder,\(\mathrm{K}_{\mathrm{C}} =\frac{1}{2} I_e \omega^2\) Equation 2
= \(\frac{1}{2} \times \frac{M R^2}{2} \times 4 \omega^2 \).
From (1) and (2),
∴ \(\frac{K_S}{K_C}=\frac{1}{5}\)
Question 32. A light rod of length / has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is:
- \(\frac{m_1 m_2}{m_1+m_2} l^2\)
- \(\frac{m_1+m_2}{m_1 m_2} l^2\)
- \(\left(m_1+m_2\right)^2\)
- \(\sqrt{m_1 m_2 l^2}\)
Answer: 1. \(\frac{m_1 m_2}{m_1+m_2} l^2\)
centre of mass of \(m_1 and m_2\) lies at
r =\(\frac{m_1 r_1+m_2 r_2}{m_1+m_2}\)
⇒ \(r_1 =\frac{m_2 l}{m_1+m_2}, r_2=\frac{m_1 l}{m_1+m_2}\)
\(I_{C M} =m_1 r_1^2+m_2 r_2^2 \)=\(m_1\left[\frac{m_2 l}{m_1+m_2}\right]^2+m_2\left[\frac{m_1 l}{m_1+m_2}\right]^2\)
=\(\frac{m_1 m_2 l^2}{\left(m_1+m_2\right)^2}\left(m_1+m_2\right)\)
=\(\frac{m_1 m_2 l^2}{m_1+m_2}\)
Class 11 Rigid Body And System Of Particles MCQs
Question 33. Two spherical bodies of masses M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body before the collision is:
- 2.5 R
- 4.5 R
- 7.5/2
- 1.5 R
Answer: 3. 7.5/2
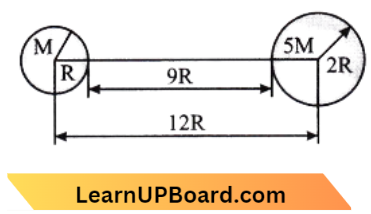
Given
Two spherical bodies of masses M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only,
Mass of one spherical body = M its radii = R
Mass of second body = 5M,
Its radii = 2R
Then we have, M x =5 M(9 R-x)
x =45 R-5 x
x =\(\frac{45 R}{6}=7.5 \mathrm{R}\)
Question 34. From a circular disc of radius R and mass 9m, a small disc of mass M and radius \(\frac{R}{3}\)is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is:
- \(\frac{40}{9} M R^2\)
- \(M R^2\)
- \(4 M R^2\)
- \(\frac{4}{9} M R^2\)
Answer: 1. \(\frac{40}{9} M R^2\)
The Moment of Inertia of a disc about an axis perpendicular to the plane and passing through the centre,
I=\(I_1-I_2 \)
I=\(\frac{9 M R^2}{2}-\frac{M R^2}{18}\)
I=\(\frac{81 M R^2-M R^2}{18}\)
I=\(\frac{40 M R^2}{9}\)
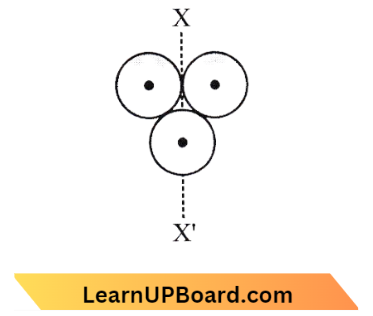
Question 35. Three identical rings of mass m and radius r are placed as shown in the figure. Find the moment of inertia of the system about axis XX’.
- \(\frac{7}{2} m r^2\)
- \(\frac{5}{2} m r^2\)
- \(\frac{3}{2} m r^2\)
- \(\frac{1}{2} m r^2\)
Answer: 1. \(\frac{7}{2} m r^2\)
Moment of Inertia Of System About XX’
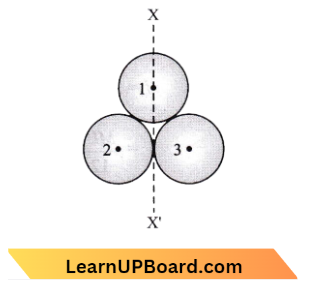
I=\(I_1+I_2+I_3\)
Here, \(I_1\)= M.I. of ring about its diameter \({1}{2} m r^2 \)
⇒ \(I_2=\frac{1}{2} m r^2+m r^2=\frac{3}{2} m r^2\)
Similarly, \(I_3=\frac{3}{2} m r^2\)
I =\(\frac{1}{2} m r^2+\frac{3}{2} m r^2+\frac{3}{2} m r^2\)
=\({7}{2} m r^2\)
Important MCQs On Rigid Body Dynamics For NEET
Question 36. The ratio of the radii of gyration of a circular disc to that of a circular ring, each of the same mass and radius around their respective axes is:
- \(\sqrt{3}: \sqrt{2}\)
- \(1: \sqrt{2}\)
- \(\sqrt{2}: 1\)
- \(\sqrt{2}: \sqrt{3}\)
Answer: 2. \(1: \sqrt{2}\)
We know that, Radius of gyration is K=\(\sqrt{\frac{I}{M}}\)
Using This Formula We Have, \(M K_1 =M R^2\)
⇒ \(K_1\) =R
And \( M K_2^2 =\frac{M R^2}{2}\)
⇒ \( K_2 =\frac{R}{\sqrt{2}}\)
∴ \(\frac{K_2}{K_1} =\frac{R}{\sqrt{2} R}=\frac{1}{\sqrt{2}}\)
Question 37. Two bodies have their moments of inertia 1 and 2 respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio:
- 2: 1
- 1: 2
- \(\sqrt{2}: 1\)
- \(1: \sqrt{2}\)
Answer: 4. \(1: \sqrt{2}\)
K.E. rotation,K=\(\frac{1}{2} I \omega^2\)
Angular momenta, L=100
K=\(\frac{L^2}{2}\)
Here, \(K_1=K_2, I_1=I_1, I_2=2 \mathrm{I}\)
⇒ \(\frac{L_1}{L_2}=\sqrt{\frac{2 I_1 K_1}{2 I_2 K_2}}\)
=\(\sqrt{\frac{I_1}{I_2}}=\sqrt{\frac{I}{2 I}}\)
=\(\frac{1}{\sqrt{2}}\)
Important MCQs On Rigid Body Dynamics For NEET
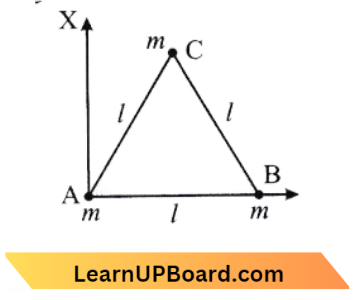
Question 38. Three particles, each of mass m gram, are situated at the vertices of an equilateral triangle ABC side/cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram cm² units will be:
- \(\frac{3}{4} m l^2\)
- \(2 m l^2\)
- \(\frac{5}{4} m l^2\)
- \(\frac{3}{2} m l^2\)
Answer: 3. \(\frac{5}{4} m l^2\)
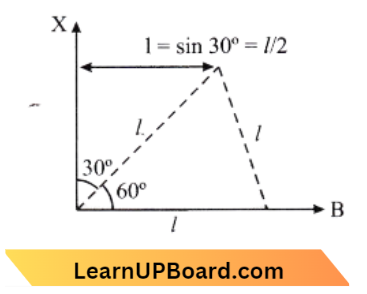
According to the question
⇒ \(I_{A X} =m l^2+m\left(\frac{l}{2}\right)^2\)
=\(m l^2+\frac{m l^2}{4}\)
=\(\frac{5}{4} m l^2\)
Question 39. A circular disc is to be made by using iron and aluminium so that it acquires a moment of inertia about the geometrical axis. It is possible with:
- aluminium at the interior and iron surrounding it
- iron at the interior and aluminium surrounding it
- using iron and aluminium lives in an alternate order
- sheet of iron is used at the external surface and aluminium sheet as internal layers
Answer: 1. aluminium in the interior and iron surrounding it
The density of Iron is more than Aluminum.
Physics MCQs For NEET with Answers
Question 40. The moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is :
- \(\frac{2}{3} M R^2\)
- \(\frac{3}{2} M R^2\)
- \(\frac{4}{5} M R^2\)
- \(\frac{5}{4} M R^2\)
Answer: 4. \(\frac{5}{4} M R^2\)
Moment of inertia of a disc about its diameter
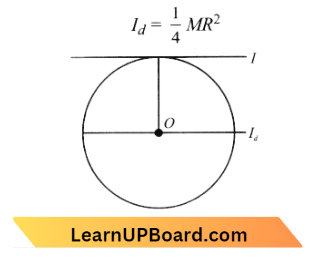
Now, according to the perpendicular axis theorem, a moment of inertia of a disc about a tangent passing through rim in the plane of the disc,
I= \(I_d+M R^2\)
I= \(\frac{1}{4} M R^2+M R^2\)
I= \(\frac{5}{4} M R^2\)
Question 41. From a disc of radius R and mass M, a circular hose of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the Centre?
- \(\frac{13 \mathrm{MR}^2}{32}\)
- \(\frac{11 \mathrm{MR}^2}{32}\)
- \(\frac{9 \mathrm{MR}^2}{32}\)
- \(\frac{15 \mathrm{MR}^2}{32}\)
Answer: 1. \(\frac{13 \mathrm{MR}^2}{32}\)
This Diagram is
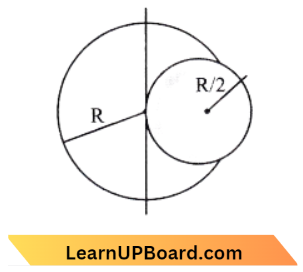
Moment of Inertia of disc,
I =\(I_1+I_2+I_3\)
⇒ \(I_1 =\frac{2}{3} m r_2\)
⇒ \(I_2 =I_3=\frac{2}{3} m r^2+m r^2\)
(using parallel axis theorem)
⇒ \(I_3=I_2 =\frac{5}{3} m r^2\)
I =\(\frac{2}{3} m r^2+2 \times \frac{5}{3} m r^2\)
= \(m r^2\left(\frac{2}{3}+\frac{10}{3}\right)=4 m r^2\)
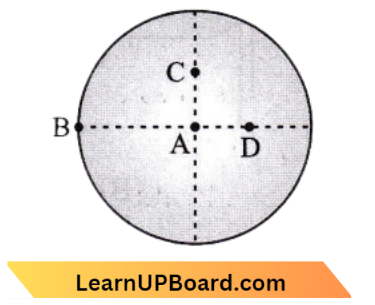
Question 42. Three identical spherical shells, each of mass m and radius r are placed as shown in the figure. Consider an axis XX, which is touching two shells and passing through the diameter of the third shell: The moment of inertia of the system consisting of these three spherical shells about XX’s axis is:
- \(\frac{11}{5} m r^2\)
- \(3 m r^2\)
- \(\frac{16}{5} m r^2\)
- \(4 m r^2\)
Answer: 4. \(4 m r^2\)
Let I1, I2 and I3 be the Movement of Inertia of three spheres
So, the Moment of Inertia of the spheres about the axis passing through xx’ is,
I=\(I_1+I_2+I_3\) Equation 1
⇒ \(I_1=\frac{2}{3} m r_2\)
⇒ \(I_2=I_3=\frac{2}{3} m r^2+m r^2\) (using parallel axis theorem)
⇒ \(I_3=I_2 =\frac{5}{3} m r^2\)
⇒ \(I =\frac{2}{3} m r^2+2 \times \frac{5}{3} m r^2\)
=\(m r^2\left(\frac{2}{3}+\frac{10}{3}\right)=4 m r^2\)
Physics MCQs For NEET With Answers
Question 43. The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:
- 2
- 3
- 4
- 1
Answer: 1. 2
According to the parallel axis theorem,\(\mathrm{I}=\mathrm{I}_{\mathrm{cm}}+m d^2\) d is maximum to B
Question 44. The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid¬point and perpendicular to its length is \(l_0\)– Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is:
- \(l_0+M L^2 / 4\)
- \(l_0+2 M L^2\)
- \(l_0+M L^2\)
- \(l_0+M L^2 / 2\)
Answer: 1. \(l_0+M L^2 / 4\)
Moment of inertia about an axis passing t}rough one end
⇒ \(\mathrm{I}=I_{C M}+m d^2 \)
∴ \(\mathrm{I}=I_0+M\left(\frac{L}{2}\right)^2=I_0+\frac{M L^2}{4}\)
Question 45. Four identical thin rods each of mass M and length l, form a square frame. The moment of inertia of this frame about an axis through the centre of the square and perpendicular to its plane is:
- \(\frac{4}{3} \mathrm{Ml}^2\)
- \(\frac{2}{3} \mathrm{Ml}^2\)
- \(\frac{13}{3} \mathrm{Ml}^2\)
- \(\frac{1}{3} \mathrm{Ml}^2\)
Answer: 1. \(\frac{4}{3} \mathrm{Ml}^2\)
From the parallel axis theorem,
Moment of Inertia =\(\frac{M l^2}{2}+M\left(\frac{1}{2}\right)^2=\frac{M l^2}{3}\)
Moment of Inertia of the system =\(\frac{M l^2}{3} \times 4\)
= \(\frac{4}{3} M l^2\)
Physics MCQs For NEET With Answers
Question 46. A thin rod of length L and mass M is bent at its midpoint into two halves so that the angle between them is 90°. The moment of inertia of the bent rod about an axis passing through the bending point and perpendicular to the plane defined by the two halves of the rod is:
- \(\frac{M L^2}{24}\)
- \(\frac{M L^2}{12}\)
- \(\frac{M L^2}{6}\)
- \(\frac{\sqrt{2} M L^2}{26}\)
Answer: 3. \(\frac{M L^2}{6}\)
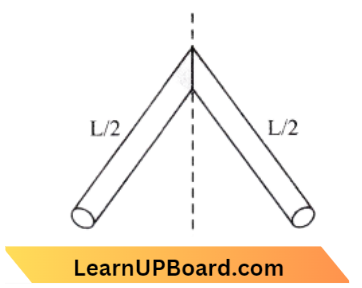
Moment of Inertia of the system, I =\(\frac{M(L / 2)^2}{3}+\frac{M(L / 2)^2}{3}\)
=\(\frac{M L^2}{12}+\frac{M L^2}{12}\)
=\(\frac{M L^2}{6}\)
Question 47. The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is:
- \(M R^2\)
- \(\frac{1}{2} M R^2\)
- \(\frac{3}{2} M R^2\)
- \(\frac{7}{2} M R^2\)
Answer: 3. \(\frac{3}{2} M R^2\)
Moment of Inertia disc about its normal =\(\frac{1}{2} M R^2\)
Moment of Inertia about its one edge =\(M R^2+\frac{M R^2}{2}\)
Moment of Inertia = \(\frac{3}{2} M R^2\)
Question 48. The ratio of the radii of gyration of a circular disc about a tangential axis in the plane of the disc and of a circular ring of the same radius about a tangential axis in the plane of the ring is:
- 2: 3
- 2: 1
- \(\sqrt{5}: \sqrt{6}\)
- \(1: \sqrt{2}\)
Answer: 3. \(\sqrt{5}: \sqrt{6}\)
The radius of gyration of the disc about a tangential axis in the plane of the disc is \(k_1\),
⇒ \(k_1=\frac{5}{4} M R^2=\frac{\sqrt{5}}{2} R\)
(From parallel Axis Theorem) And radius of gyration of a circular ring of the same radius about a tangential axis is given by:
⇒ \(k_2=\frac{3}{2} M R^2=\frac{\sqrt{3}}{\sqrt{2}} R\)
(From parallel Axis Theorem)
⇒ \(\frac{k_1}{k_2} =\frac{\sqrt{5}}{2} R / \frac{\sqrt{3}}{\sqrt{2}} R\)
=\(\frac{\sqrt{5}}{2} \times \frac{\sqrt{2}}{\sqrt{3}}\)
=\(\frac{\sqrt{5}}{\sqrt{6}}\)
Chapter-Wise MCQs For NEET Physics
Question 49. The angular speed of the wheel of a vehicle is increased from 360 rpm to 1200 rpm in 14 s. Its angular acceleration is :
- \(2 \pi \mathrm{rad} / \mathrm{s}^2\)
- \(28 \pi \mathrm{rad} / \mathrm{s}^2\)
- \(120 \pi \mathrm{rad} / \mathrm{s}^2\)
- \(1 \mathrm{rad} / \mathrm{s}^2\)
Answer: 1. \(2 \pi \mathrm{rad} / \mathrm{s}^2\)
Initial angular velocity of the wheel,
⇒ \(\omega_i =2 \pi f_o=2 \pi \times \frac{360}{60} \mathrm{rad} / \mathrm{s}\)
=\(12 \pi \mathrm{rad} / \mathrm{s}\)
final angular velocity of wheel, \(\omega_f =2 \pi f=2 \pi \times \frac{1200}{60} \mathrm{rad} / \mathrm{s}\)
=\(40 \pi \mathrm{rad} / \mathrm{s}\)
⇒ \(\Delta t=14 \mathrm{~s}\)
From the equation of rotational motion
⇒ \(\omega_f =\omega_i+\alpha \Delta t\)
⇒ \(\alpha =\frac{\omega_f-\omega_i}{\Delta t}\)
=\( 2 \pi \mathrm{rad} / \mathrm{s}\)
Question 50. A wheel has an angular acceleration of 3.0 rad/sec² and an initial angular speed of 2.00 rad sec. In a time of 2 seconds it has rotated through an angle (in radians) of:
- 10
- 12
- 4
- 6
Answer: 1. 10
⇒ \(\theta =\omega_0 t+\frac{1}{2} \alpha^2\)
=\((2)(2)+\frac{1}{2}(3)(2)^2\)
=4+6=10
Chapter-Wise MCQs For NEET Physics
Question 51. A solid cylinder of mass 2 kg and radius 4 cm is rotating about its axis at the rate of 3 rpm. The torque required to stop after the 2π revolution is :
- \(2 \times 10^{-3} \mathrm{~N}-\mathrm{m}\)
- \(2 \times 10^{-4} \mathrm{~N}-\mathrm{m}\)
- \(2 \times 10^{-6} \mathrm{~N}-\mathrm{m}\)
- \(2 \times 10^{-6} \mathrm{~N}-\mathrm{m}\)
Answer: 4. \(2 \times 10^{-3} \mathrm{~N}-\mathrm{m}\)
Mass, M=2 kg, Radius R=4 cm
Initial angular speed, \(\omega_0=3 \times \frac{2 \pi}{60} \mathrm{rad} / \mathrm{s}\)
=\(\frac{\pi}{10} \mathrm{rad} / \mathrm{s}\)
We know that, \(\omega_2 =\omega_0^2+2 \alpha \theta\)
0 =\(\left(\frac{\pi}{10}\right)^2+2 \cdot \alpha \times 2 \pi \times 2 \pi\)
⇒ \(\alpha =-\frac{1}{800} \mathrm{rad} / \mathrm{s}^2\)
Now moment of inertia of a solid cylinder,
I=\(\frac{M R^2}{2}=\frac{2 \times\left(\frac{4}{100}\right)^2}{2}=\frac{16}{10^4}\)
Now we know that, Torque,
⇒ \(\tau =\mathrm{I} \times \alpha=\frac{16}{10^4} \times\left(-\frac{1}{800}\right)\)
=\(-2 \times 10^{-6}(\mathrm{Nm})\) .
Question 52. Three objects, A : (a solid sphere), B : (a thin circular disk) and C : (a circular ring), each have the same mass M and radius R. They all spin with the same angular speed co about their symmetry axis. The amount of work (W) required to bring them to rest, would satisfy the relation :
- \(W_B>W_A>W_C\)
- \(W_A>W_B>W_C\)
- \(W_C>W_B>W_A\)
- \(W_A>W_C>W_B\)
Answer: 3. \(W_C>W_B>W_A\)
Work done required to bring them rest,
⇒ \(\Delta W =\Delta K E\)
⇒ \(W_A : W_B: W_C \)
=\(\frac{2}{5} M R^2: \frac{1}{2} M R^2: M R^2 \)
=\(\frac{2}{5}: \frac{1}{2}: 1\)
=4: 5: 10
∴ \(W_C >W_B>W_A\)
Chapter-Wise MCQs For NEET Physics
Question 53. A rope is around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder, if the rope is pulled with a force of 30 N?
- 25 m/s²
- 0.25 rad/s²
- 25 rad/s²
- 5 m/s²
Answer: 3. 25 rad/s²
Torque on the cylinder due to force F \(\tau=F R\)
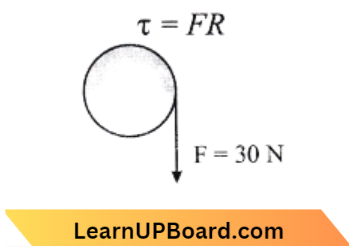
and we know that, \(\tau=\mathrm{I} \alpha\)
Where, I= Moment of Inertia of cylinder about axis = \(M R^2\)
and \(\alpha\)= angular acceleration on comparing both the equations,
⇒ \(\alpha=\frac{\tau}{I}=\frac{F R}{M R^2}=\frac{F}{M R}\)
∴ \(\alpha=\frac{30}{3 \times 40 \times 10^{-2}}=25 \mathrm{rad} / \mathrm{s}^2\)
Question 54. A uniform circular disc of radius 50 cm is at rest and is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad s-2. Its net acceleration in ms-2 at the end of 2.0 is approximately:
- 7.0
- 6.0
- 3.0
- 8.0
Answer: 4. 8.0
According to the question,
A uniform circular disc of radius 50 cm is at rest and is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected to a torque which produces a constant angular acceleration of 2.0 rad s-2.

Angular acceleration, \(\alpha=2 \mathrm{rad} \mathrm{s}^{-2}\)
Angular speed, \(\omega=\alpha t=4 \mathrm{rad} \mathrm{s}^{-1}\)
because centripetal acceleration at the end of 2.0
⇒ \(a_t=\alpha r=2 \times 0.5=1 \mathrm{~m} / \mathrm{s}^2\)
Net acceleration,\(\alpha=\sqrt{a_c^2+a_t^2}\)
=\(\sqrt{(8)^2+(1)^1}\)
=\(\sqrt{65} \approx 8 \mathrm{~m} / \mathrm{s}^2\)
Rotational Motion MCQs For NEET
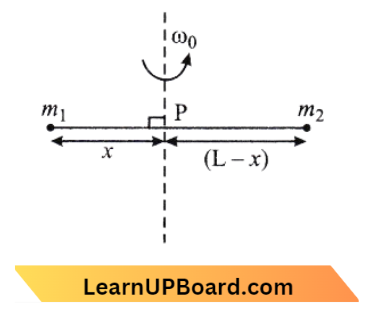
Question 55. Point masses m1 and m2 are placed at the opposite ends of a rigid rod of length L and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass, so that the work required to set the rod rotating with angular velocity COQ is minimum, is given by:
- \(x=\frac{m_1 \mathrm{~L}}{m_1+m_2}\)
- \(x=\frac{m_1}{m_2} \mathrm{~L}\)
- \(x=\frac{m_2}{m_1} \mathrm{~L}\)
- \(x=\frac{m_2 \mathrm{~L}}{m_1+m_2}\)
Answer: 4. \(x=\frac{m_2 \mathrm{~L}}{m_1+m_2}\)
Given
Point masses m1 and m2 are placed at the opposite ends of a rigid rod of length L and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point P on this rod through which the axis should pass,
Here m1 and m2 masses are placed at opposite ends of the rigid rod whose length is L
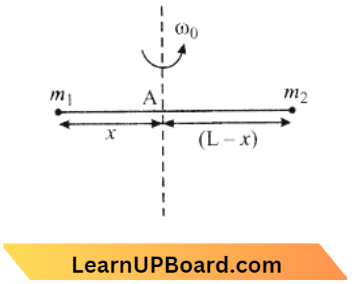
Moment of Inertia of rod, \(\mathrm{I}=m_1 x^2+m_2(L-x)^2\)
=\(m_1 x^2+m_2 L^2+m_2 x^2-2 m_2 L^2\)
⇒ \(\mathrm{I}_a is\) minima then,
⇒ \(\frac{d \mathrm{I}}{d x}=2 m_1 x+0+2 x m_2-m_2 L\) =0
⇒ \(x\left(2 m_1+2 m_2\right)=2 m_2 L\)
x=\(\frac{m_2 L}{m_1+m_2}\)
Minimum work = Minimum rotational K.E.
Maximum angular moments = Minimum moment of inertia its rotation should be about CM
∴ x=\(\frac{m_2 L}{m_1+m_2}\)
Question 56. An automobile moves on a road with a speed of 50 km hr-2. The radius of its wheels is 0.45 m and the moment of inertia of the wheel about its axis of rotation is 3 kg m². If the vehicle is brought to rest in 15 s, the magnitude to average torque transmitted by its breaks to the wheel is:
- 6.66 kg m2 s-2
- 8.58 kg m2 s-2
- 10.86 kg m2s-2
- 2.86 kg m2s-2
Answer: 1. 6.66 kg m2 s-2
Given
An automobile moves on a road with a speed of 50 km hr-2. The radius of its wheels is 0.45 m and the moment of inertia of the wheel about its axis of rotation is 3 kg m². If the vehicle is brought to rest in 15 s
According to question ,Velocity of automobile vehicle is v=\(54 \mathrm{~km} / \mathrm{h}=54 \times \frac{5}{18}\)
And angular velocity, v=\(\omega_0 r\)
⇒ \(\omega_0=\frac{v}{R}=\frac{15}{0.45}=\frac{100}{3} \mathrm{rad} / \mathrm{s}\)
and then angular acceleration is \(\alpha =\frac{\Delta \omega}{t}=\frac{\omega t-\omega_0}{t}\)
=\(\frac{0-\frac{100}{3}}{15}=-\frac{100}{15}\)
=\(-\frac{100}{15} \mathrm{rad} / \mathrm{s}^2\)
Torque, \(\tau =\mathrm{I} \alpha\)
=\(3 \times \frac{100}{45}=6.66 \mathrm{~kg} \mathrm{~m}^2 / \mathrm{s}^2\)
In Short, \(\tau=\mathrm{I} \frac{v}{t r}=\frac{3 \times 54 \times \frac{5}{18}}{15 \times 0.45}\)
∴ \(\tau=6.66 \mathrm{~kg} \mathrm{~m}^2 / \mathrm{s}^2\)
Rotational Motion MCQs For NEET
Question 57. A solid cylinder of mass 50 kg and radius 0.5 m is free to rotate about the horizontal axis. A massless string is wound around the cylinder with one end attached to it and the other hanging freely. Tension in the string required to produce an angular acceleration of 2 rev/s² is:
- 25 N
- 50 N
- 78.5 N
- 157 N
Answer: 4. 157 N
According to the question, the Mass of the cylinder, M= 50 kg.
The radius of the cylinder,
R = 0.5 m
Angular acceleration = \(\alpha=2 \mathrm{rev} / \mathrm{s}^2\)
We know that torque, \(\tau=\mathrm{I} \alpha\) → Equation 1
Now torque produced in the string is \(\alpha=T \times R=T \times 0.5=\frac{T}{2}\) → Equation 2
From equation 1 And 2
α = \(\frac{T}{2}\)
⇒ \(\frac{T}{2} =\left(\frac{M R^2}{2}\right) \times 2 \times 2 \pi\)
I =\(\frac{M R^2}{2}\)
⇒ \(\frac{T}{2} =\frac{50 \times(0.5)^2}{2} \times 4 \pi\)
I = \(50 \times \frac{1}{4} \times 4 \pi=50 \pi\)
=157 \(\mathrm{~N}\)
Question 58. A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When a string is cut, the initial angular acceleration of the rod is:
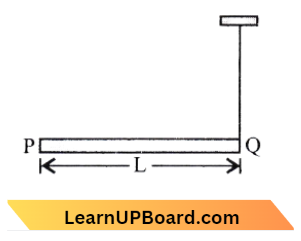
- \(\frac{3 g}{2 \mathrm{~L}}\)
- \(\frac{g}{\mathrm{~L}}\)
- \(\frac{2 g}{\mathrm{~L}}\)
- \(\frac{2 g}{3 \mathrm{~L}}\)
Answer: 1. \(\frac{3 g}{2 \mathrm{~L}}\)
Torque on the rod = Moment of the rod P
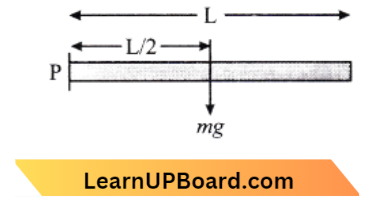
T= \(m g_{\frac{1}{2}}\) → Equation 1
The moment of inertia of the rod about P,
P= \(\frac{m L^2}{3}\) → Equation 2
From equation. (1) and (2), Since \(\mathrm{T}=\mathrm{I}\)α
⇒ \(m g \frac{1}{2} =\frac{m \mathrm{~L}^{\not}}{3} \alpha\)
∴ \(\alpha =\frac{3 g}{2 L}\)
Rotational Motion MCQs For NEET
Question 59. The instantaneous angular position of a point on a rotating wheel is given by the equation, Q(t) = 2/3 – 6/3. The torque on the wheel becomes zero at:
- t = 0.5 x
- t = 0.25 x
- t = 2s
- t = 1s
Answer: 4. t = 1 ,v
Given \(\theta(t)=2 t^3 -6 t^2\)
⇒ \(\frac{d \theta}{d t} =6 t^2-12 t\)
⇒ \(\frac{d^2 \theta}{d t^2}\) =12 t-12
It is given that, torque \( \tau\)=0 means \(\alpha \)=0 and
⇒ \(\alpha =\frac{d^2 \theta}{d t^2}\)=0
12 t-12 =0
t =1 sec
Question 60. A uniform rod AB of length L and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of. the rod about A is mP²/3, the initial angular acceleration of the rod will be :
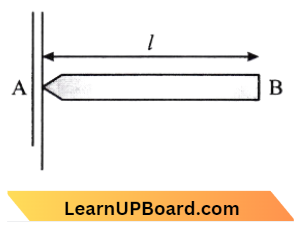
- \(\frac{m g l}{2}\)
- \(\frac{3}{2} g l\)
- \(\frac{3 g}{2 l}\)
- \(\frac{2 g}{3 l}\)
Answer: 1. \(\frac{m g l}{2}\)
Torque About A,

⇒ \(\tau=m g \times \frac{l}{2}=\frac{m g l}{2}\)
⇒ \(\tau=I \alpha\)
∴ Also, Angular Acceleration \(\alpha=m g \times \frac{l}{2}=\frac{m g l}{2}\)
Rotational Motion MCQs For NEET
Question 61. A wheel having moment of inertia 2 kg m² about its vertical axis, rotates at the rate of 60 rpm about the axis. The torque which can stop the wheel’s rotation in one minute would be:
- \(\frac{2 \pi}{15} \mathrm{~N}-\mathrm{m}\)
- \(\frac{\pi}{12} \mathrm{~N}-\mathrm{m}\)
- \(\frac{\pi}{15} \mathrm{~N}-\mathrm{m}\)
- \(\frac{\pi}{18} \mathrm{~N}-\mathrm{m}\)
Answer: 3. \(\frac{\pi}{12} \mathrm{~N}-\mathrm{m}\)
Given, \(\mathrm{I} =2 \mathrm{~kg} m^2,\)
⇒ \(\omega_0 =\frac{60}{60} \times 2 \pi \mathrm{rad} / \mathrm{s}\)
t =60s
The torque required to stop the wheel’s rotation is,
⇒ \(\tau =\mathrm{I} \alpha l\left(\frac{\omega_0-\omega}{t}\right)\)
⇒ \(\tau =\frac{2 \times 2 \pi \times 60}{60 \times 60}\)
=\(\frac{\pi}{15} \mathrm{~N}-\mathrm{m}\)
Question 62. A solid sphere is rotating freely about its symmetry axis in free space. The radius of the sphere is increased keeping its mass the same. Which of the following physical quantities would remain constant for the sphere?
- Rotational kinetic energy
- Moment of inertia
- Angular velocity
- Angular momentum
Answer: 4. Angular momentum
From question,
External torque, \(\tau\) =0
⇒ \(\frac{d \mathrm{~L}}{d t}\) =0
L = Constant
So, angular momentum remains constant.
System Of Particles And Rigid Body Questions For NEET
Question 63. Two discs of the same moment of inertia rotate about their regular axis passing through the centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is:
- \(\frac{1}{2}\left(\omega_1+\omega_2\right)^2\)
- \(\frac{1}{4}\left(\omega_1-\omega_2\right)^2\)
- \(l\left(\omega_1-\omega_2\right)^2\)
- \(\frac{1}{8}\left(\omega_1+\omega_2\right)^2\)
Answer: 2. \(\frac{1}{4}\left(\omega_1-\omega_2\right)^2\)
Using the law of conservation of angular momentum,
Angular moments before contact = \(I_1 \omega_1+I_2 \omega_2\)
Angular momentum after contact = \(I_\omega\)
⇒ \(\left(I_1+I_2\right) \omega\)
⇒ \(\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)
Loss of energy =\(\frac{1}{2} I \omega_1^2+\frac{1}{2} I \omega_2^2-\frac{1}{2}(2 I) \omega^2\)
= \(\frac{1}{4} I\left(\omega_1-\omega_2\right)^2\)
Question 64. The rotating bodies A and B of masses m and 2m with moments of inertia and IB(IB > IA) have equal kinetic energy of rotation. If LA and LB are their angular momenta respectively, then:
- \(L_A=\frac{L_B}{2}\)
- \(L_A=2 L_B\)
- \(L_B>L_A\)
- \(L_A>L_B\)
Answer: 3. \(L_B>L_A\)
The K.E. of a rotating body is, \(K E=\frac{1}{2} I \omega^2=\frac{1}{2} \frac{I^2 \omega^2}{I}=\frac{L^2}{2 I}\)
⇒ \((Since L=I \omega )\)
From question \(K_A=K_B\)
⇒ \(\frac{L_A^2}{2 I_A}=\frac{L_B^2}{2 I_B}\)
As, \(I_B>I_A\)
So,\(L_A^2<L_B^2\)
∴ \(L_A<L_B\)
Question 65. The 2 discs are rotating about their axis, normal to the plane of the discs and passing through the centre of the discs. Disc D, has a 2 kg mass and 0.2 m radius and an initial angular velocity of 50 rad s-1. Disc D1 has a 4 kg mass, 0.1 m radius and an initial angular velocity of 200 rad s-1. The two discs are brought in contact face to face, with their axes of rotation coincident. The final angular velocity (in rad,s-1) of the system is:
- 60
- 100
- 120
- 40
Answer: 2. 100
Moment of Inertia of\(I_1=\frac{\mathrm{MR}^2}{2}=\frac{2(0.2)^2}{2}=0.04\) kg-m² initial angular velocity of \(I_2=\frac{4 \times(0.1)^2}{2}\)rad S-1 M.J of D² is \(\omega_2=200\)= 0.02 kg m² initial angular velocity of D² fs co² = 200 and S-1.
According to the law of conservation of angular momentum \(L_1 =L_2\)
⇒ \(\mathrm{I}_1 \omega_1+\mathrm{I}_2 \omega_2 =\left(\mathrm{I}_1+\mathrm{I}_2\right)\)
⇒ \(\omega =\frac{I_1 \omega_1+I_2 \omega_2}{I_1+I_2}\)
⇒ \(\omega =\frac{(0.04)^2 \times 50+(0.02)^2 \times 200}{0.04+0.02}\)
=\(\frac{2+4}{0.06}=100 \mathrm{rads}^{-1}\)
System Of Particles And Rigid Body Questions For NEET
Question 66. A thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity. If two objects each of mass m are attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity
- \(\frac{\omega(W-2 m)}{M+2 m}\)
- \(\frac{\omega M}{M+2 m}\)
- \(\frac{\omega(M+2 m)}{M}\)
- \(\frac{\omega M}{M+m}\)
Answer: 2. \(\frac{\omega M}{M+2 m}\)
Applying the law of conservation of angular momentum 7icoi = I2to2
It is given that: I = MR2
⇒ \(I_2 =M R^2+2 m R^2\)
⇒ \(\omega_1 =\omega_2\)
⇒ \(\omega_2 =\frac{I_1}{I_2} \omega\)
=\(\frac{M}{M+2 m} \omega\)
Question 67. A circular disc of the moment of inertia It is rotating in a horizontal plane, about its symmetry axis, with a constant angular speed to, Another disk of moment of inertia, is dropped coaxially onto the rotating disk. Initially, the second disk has zero angular speed. Eventually, both the disks rotate with a constant angular speed toy. The energy lost by the initially rotating disc due to friction is:
- \(\frac{1}{2} \frac{I_b^2}{\left(I_t+I_b\right)} \omega_i^2\)
- \(\frac{1}{2} \frac{I_t^2}{\left(I_t+I_b\right)} \omega_i^2\)
- \(\frac{1}{2} \frac{I_b-I_t}{\left(I_t+I_b\right)} \omega_i^2\)
- \(\frac{1}{2} \frac{I_b I_t}{\left(I_t+I_b\right)} \omega_i^2\)
Answer: 4. \(\frac{1}{2} \frac{I_b I_t}{\left(I_t+I_b\right)} \omega_i^2\)
Loss of energy is \(\Delta\)E
⇒ \(\Delta E =\Delta E_i-\Delta E_f \)
=\(\frac{1}{2} I_t \omega_i^2-\frac{1}{2} \frac{I_i^2 \omega_i^2}{\left(r_e+I_B\right)}\)
=\(\frac{1}{2} \frac{I_b I_t \omega_i^2}{\left(I_t+I_b\right)}\)
Question 68. A round disc of the moment of inertia/2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of the moment of inertia I rotating with an angular velocity ω about the same axis. The final angular velocity of the combination of discs is:
- \(\frac{I_2 \omega_1}{I_2+I_2}\)
- \(\frac{\omega\left(I_1+I_2\right)}{I_2}\)
- \(\frac{I_1 \omega_1}{I_1+I_2}\)
- \(\frac{\left(I_1+I_2\right) \omega_1}{I_1}\)
Answer: 3. \(\frac{I_1 \omega_1}{I_1+I_2}\)
Given
A round disc of the moment of inertia/2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of the moment of inertia I rotating with an angular velocity ω about the same axis.
From the law of conservation of angular momentum we have :
⇒ \(I_1 \omega_1 \equiv\left(I_1+I_2\right) \omega_2\)
∴ \(\omega_2 =\frac{I_1 \omega_1}{\left(I_1+I_2\right)}=\frac{I_1 \omega}{I_1+I_2}\)
System of Particles and Rigid Body Questions for NEET
Question 69. A thin circular ring of Mass M and radius r is rotating about its axis with a constant angular velocity co. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be:
- \(\frac{M \omega}{4 m}\)
- \(\frac{M \omega}{M+4 m}\)
- \(\frac{(M+4 m) \omega}{M}\)
- \(\frac{(M-4 m) \omega}{M+4 m}\)
Answer: 2. \(\frac{M \omega}{M+4 m}\)
Given
A thin circular ring of Mass M and radius r is rotating about its axis with a constant angular velocity co. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring.
According to the law of conservation of angular momentum
⇒ \(M r^2 \omega =\left(M r^2+4 m r^2\right) \omega^{\prime}\)
∴ \(\omega^{\prime} =\frac{M \omega}{M+4 m}\)
Question 70. A disc is rotating with angular speed co. If a child sits on it, what is conserved?
- Linear momentum
- Angular momentum
- Kinetic energy
- Potential energy
Answer: 2. Angular momentum
\(\tau =\frac{d L}{d t}, \text { so }\)=0
L =\(\frac{d L}{d l}\)constant
Law of conservation of angular momentum.
Question 71. At any instant, a rolling body may be considered to be in pure rotation about an axis through the point of contact. This axis is translating forward with speed :
- equal to the centre of mass
- zero
- twice of centre of mass
- None of the above
Answer: 1. equal to the centre of mass
Since the instantaneous axis of rotation is always below the centre of mass in this case. This is only possible if the point of contact moves at the same speed as the centre of mass
Question 72. A solid cylinder of mass 2 kg and radius 50 cm rolls up an inclined plane of angle inclination 30°. The centre of mass of the cylinder has a speed of 4 m/s. The distance travelled by the cylinder on the inclined surface will be : (Take g = 10 m/s²)
- 2.2 m
- 1.6 m
- 1.2 m
- 2.4 m
Answer: 4. 2.4 m
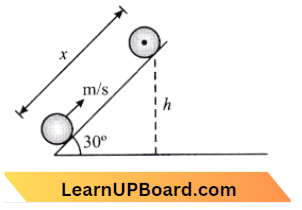
Since, v= \(\sqrt{\frac{2 g h}{1+\frac{\mathrm{K}^2}{\mathrm{R}^2}}}\)
⇒ \(v^2= \frac{2 g h}{1+\frac{1}{2}}\)
⇒ \(\left[\frac{\mathrm{K}^2}{\mathrm{R}^2}=\frac{1}{2} \text { for solid cylinder }\right]\)
2 g h =\(4^2 \times \frac{3}{2}\)
h =\(\frac{12}{10}=1.2 \mathrm{~m}\)
∴ Now, X =\(\frac{h}{\sin 30^{\circ}}=\frac{1.2}{\frac{1}{2}}=2.4 \mathrm{~m}\)
Motion Of System Of Particles NEET Questions
Question 73. A solid sphere is in a rolling motion. In rolling motion, a body possesses translational kinetic energy (K,) as well as rotational kinetic energy (Kr) simultaneously. The ratio K,: (K, + Kr) for the sphere is :
- 10: 7
- 5: 7
- 7: 10
- 2: 5
Answer: 3. 7: 10
Given
A solid sphere is in a rolling motion. In rolling motion, a body possesses translational kinetic energy (K,) as well as rotational kinetic energy (Kr) simultaneously.
The translational kinetic energy of the rolling body,
Total kinetic energy = Rotational KE + Translational KE = latex]k_t+k_r[/latex]
(Solid sphere I=\(\frac{2}{5} M R^2)\)
= \(k_t+k_r\)
=\( \frac{1}{2}\left(\frac{2}{5} M R^2\right) \omega^2+\frac{1}{2} m v^2\)
=\( \frac{1}{2}\left(\frac{2}{5} M R^2\right)\left(\frac{V}{R}\right)^2+\frac{1}{2} m v^2\)
=\( \frac{1}{5} m v^2+\frac{1}{2} m v^2=\frac{7}{10} m v^2\)
Ratio = \(\frac{k_t}{k_t+k_2}=\frac{\frac{1}{2} m v^2}{\frac{7}{10} m v^2}\)
=\(\frac{1}{2} \times \frac{10}{7}=\frac{5}{7}\)=5: 7
Question 74. A disc and a sphere of the same radius but different masses roll off on two inclined planes of the same altitude and length. Which one of the two objects gets to the bottom of the plane first?
- Both reach at the same time
- Depends on their masses
- Disc
- Sphere
Answer: 4. Sphere
The time taken by the body to reach the bottom when it rolls down on an inclined plane without slipping is given by
⇒ \(t=\sqrt{\frac{2 l\left(1+\frac{k^2}{R^2}\right)}{g \sin \theta}}\)

Question 75. The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is :
- 5: 7
- 2 : 3
- 2: 5
- 7: 5
Answer: 1. 5: 7
In this question, there are two cases. First when a solid sphere rolls without slipping down an inclined plane and second a sphere slips down in the inclined plane.
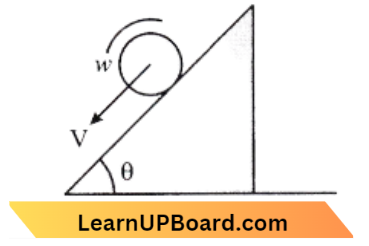
First Case
\(a_1 =\frac{g \sin \theta}{1+\frac{k^2}{\mathrm{R}^2}}\)=\(\frac{g \sin \theta}{1+\frac{(215) R^2}{R^2}}\) → Equation 1
⇒ \(a_1 =\frac{5 g \theta}{7}-6\) (Since, solid sphere \(k^2=\frac{2}{5} R^2)\)
Second case
\(a^2=g \sin \theta\) → Equation 2
From (1) and (2),
⇒ \(\frac{a_1}{a_2}=\frac{\frac{5}{7} g \sin \theta}{g \sin \theta}=\frac{5}{7}\)
∴ \(\frac{a_1}{a_2}=\frac{5}{7}\)
Motion Of System Of Particles NEET Questions
Question 76. A small object of uniform density rolls up a curved surface with an initial velocity of V. It reaches up to a maximum height of\(\frac{3 v^2}{4 g}\) concerning the initial position. The object is:
- hollow sphere
- disc
- ring
- solid sphere
Answer: 2. disc
Given
A small object of uniform density rolls up a curved surface with an initial velocity of V. It reaches up to a maximum height of\(\frac{3 v^2}{4 g}\) concerning the initial position.
The Kinetic energy of the rolling object is converted into potential energy at height
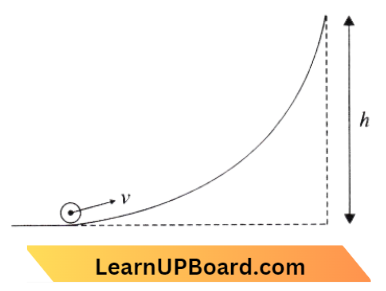
So by the law of conservation of mechanical energy, we have
⇒ \(\frac{1}{2} M v^2+\frac{1}{2} I \omega^2\) =M g h
⇒ \(\frac{1}{2} M v^2+\frac{1}{2}\) I\((\frac{v}{R})^2\) =Mg \((\frac{3 v^2}{4 g})\)
⇒ \(\frac{1}{2} I \frac{v^2}{R^2} =\frac{3}{4} M v^2-\frac{1}{2} M v^2\)
⇒ \(\frac{1}{2} I \frac{v^2}{R^2} =\frac{1}{4} M v^2\)
or I =\(\frac{1}{2} M R^2\)
Question 77. A solid cylinder of mass 3 kg is rolling on a horizontal surface with a velocity of 4 ms-1. It collides with a horizontal spring of force constant 200 Nm-1. The maximum compression produced in the spring will be the:
- 0.5 m
- 0.6 m
- 0.7 m
- 0.2 m
Answer: 1. 0.5 m
At maximum compression, the solid cylinder will stop.
According to the law of conservation of mechanical energy Loss in kinetic energy of the cylinder = Gain in the potential of the spring
⇒ \(\frac{1}{2} m v^2+\frac{1}{2} I \omega^2=\frac{1}{2} k x^2\)
⇒ \(\frac{1}{2} m v^2+\frac{1}{2}\left(\frac{m R^2}{2}\right)\left(\frac{v}{R}\right)^2=\frac{1}{2} k x^2\)
v\(=R \omega\) and for solid cylinders. \(\left.I=\frac{1}{2} m R^2\right)\)
⇒ \(\frac{1}{2} m v^2+\frac{1}{4} m v^2 =\frac{1}{2} k x^2 \) or,
⇒ \(\frac{3}{4} m v^2 =\frac{1}{2} k x^2 \) or
⇒ \(x^2 =\frac{3}{2}=\frac{m v^2}{k}\)
Here, m-3 kg, v = 4ms-1, A: = 200 Nm-1 Substituting the given values, we get
⇒ \(x^2=\frac{3 \times 3 \times 4 \times 4}{2 \times 200}\)
∴ \(x^2=\frac{36}{60} \text { or } x=0.6 \mathrm{~m}\)
Question 78. The solid cylinder and a hollow cylinder both of the same mass and same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which one will reach the bottom first?
- Both together only when the angle inclination of the plane is 45°
- Both together
- Hollow cylinder
- Solid cylinder
Answer: 4. Solid cylinder
Given
The solid cylinder and a hollow cylinder both of the same mass and same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping.
T =\(\frac{1}{\sin \theta} \sqrt{\frac{2 h}{g}\left(1+\frac{K^2}{R^2}\right)}\)
⇒ \(\text { ce, }\left(\frac{K^2}{R^2}\right)_S <\left(\frac{K^2}{R^2}\right)_H\)
Solid-body will reach the bottom first with greater velocity
Question 79. A roller coaster is designed such that riders experience “weightlessness” as they go around the top of a hill whose radius of curvature is 20 m. The speed of the car at the top of the hill is between:
- 14 m/s and 15 m/s
- 15 m/s and 16 m/s
- 16 m/s and 17 m/s
- 13 m/s and 14 m/s
Answer: 1. 14 m/s and 15 m/s
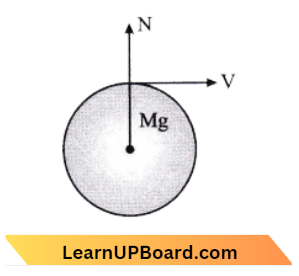
Balancing the force,M g-N= \(\frac{M v^2}{r}\)
When N=0 for weightiness
⇒ \(\frac{M v^2}{r} =\mathrm{Mg}\)
⇒ \(v^2 =g r=20 \times 10=200 \)
v =\(\sqrt{200}=14.14 \mathrm{~m} / \mathrm{s}\)
Question 80. A drum of radius R and mass M rolls down without slipping along an inclined plane of angle θ. The frictional force:
- dissipates energy as heat
- decreases the rotational motion’
- decreases the rotational and translational motion
- converts translational energy
Answer: 4. converts translational energy
Required frictional force converts translational energy into rotational energy.
Motion Of System Of Particles NEET Questions
Question 81. A drum of radius R and mass M rolls down without slipping along an inclined plane of angle θ. The frictional force:
- dissipates energy as heat
- decreases the rotational motion
- decreases the rotational and translational motion
- converts translational energy to rotational energy.
Answer: 4. converts translational energy to rotational energy.
Required frictional force converts some part of translational energy into rotational energy
Question 82. A solid cylinder of mass M and radius R rolls without slipping an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom?
- \(\sqrt{2 g h}\)
- \(\sqrt{\frac{3}{4} g h}\)
- \(\sqrt{\frac{4}{3} g h}\)
- \(\sqrt{4 g h}\)
Answer: 2. \(\sqrt{\frac{3}{4} g h}\)
Here, K.E. of the centre of mass when the cylinder reached the bottom\(\frac{1}{2} m v^2+\frac{1}{2} \mathrm{I} \omega^2\) → Equation 1
Here, I =\(\frac{1}{2} M K^2\)
And \(\omega =\frac{v}{R}\)
⇒ \(\mathrm{KE} =\frac{1}{2} m v^2+\frac{1}{2} M K^2 \cdot \frac{v^2}{r^2}\)
= \(\frac{1}{2} m v^2\left[1+\frac{K^2}{R^2}\right]\)
But for solid Cylinder,\(\frac{R}{\sqrt{2}}\)
Or \(\frac{K^2}{R^2}=\frac{1}{2}\)
K E=\(\frac{3}{4} m v^2\) → Equation 2
PE of the solid cylinder at height h is PE = mgh → Equation 3
From Equation (2) and (3)
mg =\(\frac{3}{4} m v^2 \)
v = \(\sqrt{\frac{3}{4} g h}\)
Question 83. A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is K. If the radius of the ball is R, then the fraction of total energy associated with its rotational energy will be:
- \(\frac{K^2+R^2}{R^2}\)
- \(\frac{K^2}{R^2}\)
- \(\frac{K^2}{K^2+R^2}\)
- \(\frac{R^2}{K^2+R^2}\)
Answer: 3. \(\frac{K^2}{K^2+R^2}\)
Total energy = \(\frac{1}{2} I \omega^2+\frac{1}{2} m v^2\)
= \(\frac{1}{2} m v^2\left(1+\frac{K^2}{R^2}\right)\)
Rotational energy = \(\frac{1}{2} I \omega^2\)
= \(\frac{K^2+R^2}{1+\frac{K^2}{R^2}}\)
Required fraction = \(\frac{K^2 / R^2}{1+K^2 / R^2}\)
= \(\frac{K^2}{R^2+K^2}\)
Question 84. A solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height ‘h’ from the lowest point. For the maximum acceleration of the centre of mass, which is correct?
- h = R
- h = 2R
- h = 0
- No relation between h and R
Answer: 4. No relation between h and R
A smooth surface is given so rolling motion is not possible. Sphere will perform linear motion
Question 85. Consider a point P at the contact point of a wheel on the ground which rolls on the ground without slipping, then the value of the displacement of point P when the wheel completes half of the rotation (if the radius of the wheel is 1 m) is:
- \(2 \mathrm{~m}\)
- \(\sqrt{\pi^2+4} \mathrm{~m}\)
- \(\pi \mathrm{m}\)
- \(\sqrt{\pi^2+2} \mathrm{~m}\)
Answer: 2. \(\sqrt{\pi^2+4} \mathrm{~m}\)
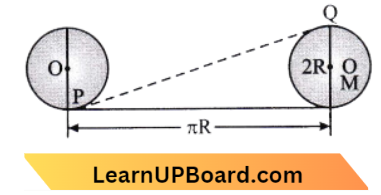
Displacement PQ=\(\sqrt{(PM)^2+(Q M)^2}\)
⇒ \(\sqrt{(\pi R)^2+(2 R)^2}\)
∴ \(\sqrt{\pi^2+4}\)
Motion Of System Of Particles NEET Questions
Question 86. A disc is rolling, and the velocity of its centre of mass is Vcm. Which one will be correct?
- The velocity of the highest point is 2vcm and at the point of contact is zero.
- The velocity of the highest point is vcm and at the point of contact is vcm.
- The velocity of the highest point is 2vcm and the point of contact is vcm.
- The velocity of the highest point is 2vcm and the point of contact is 2vcm.
Answer: 1. The velocity of the highest point is 2vcm and at the point of contact is zero
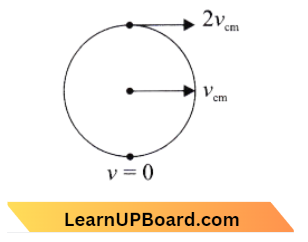
Question 87. A solid spherical ball rolls on a table. The ratio of its rotational kinetic energy to total kinetic energy is:
- 1/2
- 1/6
- 7/10
- 2/7
Answer: 4. 2/7
Linear K.E. of ball=\(\frac{1}{2} m v^2\) and
rotational K.E. of ball =\(\frac{1}{2} I \omega^2\)
=\(\frac{1}{2}\left(\frac{2}{5} m r^2\right) \omega^2=\frac{1}{5} m v^2\)
Total K. E. =\(\frac{1}{2} m v^2+\frac{1}{5} m v^2=\frac{7}{10} m v^2\)
Ratio of rotational K.E. and total K.E. =\(\frac{(1 / 5) m v^2}{(7 / 10) m v^2}=\frac{2}{7}\)
Question 88. A solid sphere, disc and solid cylinder all of the same mass and radius are allowed to roll down (from rest) on the inclined plane, then:
- solid sphere reaches the bottom first
- solid sphere reaches the bottom last
- the disc will reach the bottom first
- all reach the bottom at the same time.
Answer: 1. solid sphere reaches the bottom first
For solid sphere\(\frac{K^2}{R^2}=\frac{2}{5}\)
For disc and solid cylinder,\(\frac{K^2}{R^2}=\frac{1}{2}\)
As for the solid sphere \(, K^2 / R^2\) is the smallest, it takes minimum time to reach the bottom of the incline, disc and cylinder reach together later.
Question 89. The speed of a homogenous solid sphere after rolling down an inclined plane of vertical height h from rest without sliding is:
- \(\sqrt{\frac{10}{7} g h}\)
- \(\sqrt{g h}\)
- \(\sqrt{\frac{6}{5} g h}\)
- \(\sqrt{\frac{4}{3} g h}\)
Answer: 1. \(\sqrt{\frac{10}{7} g h}\)
PE. = total K.E.
∴ \(m g h=\frac{7}{10} m v^2, v=\sqrt{\frac{10 g h}{7}}\)
Motion Of System Of Particles NEET Questions
Question 90. A solid homogenous sphere of mass M and radius is moving on a rough horizontal surface, partly rolling and partly. During this kind of motion of the sphere:
- total kinetic energy is conserved
- the angular momentum of the sphere about the point of contact with the plane is conserved
- only the rotational kinetic energy about the centre of mass is conserved
- angular momentum about the centre of mass is conserved.
Answer: 2. the angular momentum of the sphere about the point of contact with the plane is conserved
Angular momentum about the point of contact with the surface includes the angular momentum about the centre. Because of friction, linear momentum will not be conserved.
